Received 13 February 2015; accepted 3 March 2015; published 4 March 2015

ABSTRACT

This paper extends the results of Saint-Paul (2007) regarding the long-run survival rates of alleles in trading populations, to a more general context where the number of loci is arbitrarily large under general assumptions about sexual reproduction. The central result is that fitness-reducing alleles can survive in a trading population, provided their frequency is not too large. However, the greater the number of loci that matter for fitness, the more stringent the conditions under which these alleles can survive.

Keywords:

Gene-Culture Coevolution, Markets, Division of Labor, Population Genetics

1. Introduction

Can culture affect the genetic makeup of a population? While this question has been dealt with some detail regarding cultural institutions such as cooperation and social norms,¹ there is much less work dealing with a key component of culture: markets.² Do we expect populations who trade for long enough to develop a different distribution of alleles compared with population where individuals remain in relative autarky?

In Saint-Paul [8] ,³ I consider the evolution of the gene pool in a population under alternative economic institutions, and show that alleles that cannot survive natural selection under autarky can survive under trade, because individuals can specialize in activities so as to avoid the fitness disadvantages associated with these alleles. The results are based on a very simplified representation of sexual reproduction, with only one chromo- some (instead of pairs of chromosomes), and only two loci that determine the individual’s productivity at two activities that affect fitness.

This paper generalizes these results for a more general system of sexual reproduction, with an arbitrary number of chromosomes and loci. Its contribution is twofold. First, it provides a set of assumptions under which one can meaningfully state that some alleles dominate their alternatives and eventually eliminate them in the long run. Second, it extends the results in Saint-Paul [8] by characterizing the distribution of alleles for a trading population in a long-run equilibrium (LRE), defined as a stationary distribution of alleles which is also an equilibrium in an economic sense.

The central result is that fitness-reducing alleles can survive in a trading population, provided their frequency is not too large. However, the greater the number of loci that matter for fitness, the more stringent the conditions under which these alleles can survive. That means that in the long run, we expect low alleles to survive only at a relatively small number of loci. Knowing more about the long-run distribution of alleles when their initial distribution does not satisfy the conditions for an LRE would involve analyzing the dynamics, which I do not do here but is an interesting topic for further research.

2. Notations and Genetic Properties of Stationary Populations

A genotype consists of an 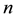-tuple, where 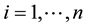denotes a particular locus, and is interpreted as the number of alleles of the “high type” at locus 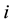(in the actual world where chromosomes come by pairs, one has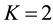). Therefore, there are 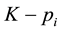alleles of the “low type” at locus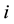. The set of possible genotypes is denoted by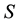. We will also denote by the 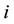th element of.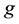

2.1. The Survival Function

The survival rate of an individual only depends on its genotype, and is denoted by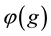. Note that the 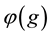function is not independent of culture. The opportunity to trade and specialize will dramatically change the mapping. It is useful to introduce the genetic improvement operators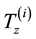, which, for any genotype such that, maps it into another genotype, defined by, and. Note that.

The survival function is monotonic at locus if it satisfies

(1)

Thus, having more of a high allele at locus cannot increase mortality, everything else equal. Note that this assumes that the role played by an allele in mortality has the same sign regardless of what other alleles are present.

We will say that a locus is selective if

(2)

2.2. The Distribution of Offsprings

We assume a quite general process for transmitting genes to offsprings, which in particular is compatible with real-world genetics. When genotypes and mate, the fraction of their offsprings with genotype is given by a probability distribution function. We shall assume that it satisfies the following properties:

1. Gene conservation

(3)

This says that on average, the number of high alleles at locus among offsprings, denoted by, is equal to the its average between the two parents. For a given pair of parents, the average among actual off- springs will be different from the parental average. However, with a continuum of individuals, the law of large number will apply, and will be equal to the population average of the number of H-alleles at among all offsprings of all couples with genotypes and.

2. Allele independence

(4)

This assumption tells us that, among offsprings with the same parental genotypes, the distribution of other genes among those who have the same number of high alleles at locus, does not depend on that particular number. If that property did not hold, having many good alleles at one locus could in principle be systematically correlated with having many bad alleles at another locus, and this complementarity could sustain a positive amount of mortality-increasing alleles in the long-run, or, conversely, eliminate mortality-reducing ones.

3. Mixing

For any, , for all such that

(5)

there exists such that, for, and.

The RHS of (5) is the maximum number of H-alleles at locus if one inherits alleles from each parent; the LHS is the minimum number of H-alleles. That assumptions says that for any number between these two bounds, there is a positive probability for a couple, to have an offspring with exactly that number. Furthermore, we can pick up that offspring such that at all other loci, its number of high alleles is between that of its two parents. Loosely speaking, that means that the distribution of offsprings spans all possible cases.

4. Symmetry

(6)

5. Monotonicity

For any, any, any such that, and any such that

(7)

(8)

This assumption says that if instead of, a genetically improved genotype at locus mates with, then holding the alleles at other loci constant, the proportion of H-alleles at locus improves in a first-order stochastic dominance sense: offsprings are more likely to have a higher umber of H-alleles at. Formally, applying the operators starting from an initial genotype such that, allows to compute the marginal distribution of among offsprings holding other alleles constant. The last equality says that the partial distribution of the genotype at all other loci except is invariant when one mates with a genetic improvement of at instead of.

2.3. Demographics

These assumptions allow to write down the demographic evolution equations of each genotype. We denote by total population at date and by the fraction of people with genotype. People mate randomly.

There are matches of types and at date. They produce offpsrings, and a frac- tion of offsprings with genotype reach maturity. Consequently, evolves according to

Adding all these equations across all possible genotypes we get that

It is also useful to define the population frequency of high alleles at locus:

Note that if the gene conservation law holds, then one also has

(9)

3. Elimination of Less Fit Alleles

In this section, I provide the basic results regarding the elimination of less fit alleles. A first lemma, which derives from the random mating and mixing properties, states that if a genotype exists and if a high allele exists in the population at locus, then we can find another genotype that differs from it only in that it is “improved” at locus, unless, of course, the initial genotype has the maximum number of H-alleles at.

LEMMA 1―Assume the mixing property holds. Assume there exists a steady state, a locus and a genotype such that in that steady state, , , and. Then.

PROOF―First note that because of random mating there exists a positive measure of matches between two arbitrary genotypes, provided these genotypes are in positive measure in the parent population.

If, the mixing property applied at locus implies that offsprings of with itself include with positive probability. Assume. Since, there exists such that and. We can then iterate the mixing property, by looking at stage at the mates between and, starting with. If at stage, there exists such that, say, by applying

the mixing property at locus we know that among the offsprings between and, there exists one such that―implying in steady state―, and . In other words, the “genetic distance” between and strictly goes down with. Once we have reached the stage where for all, we apply the same procedure to locus, until we have produced an offspring such that, and.

At that stage. Q.E.D.

The following key result tells us that genes which increase mortality eventually disappear:

PROPOSITION 1―Assume that one of these two conditions holds:

(i) locus is selective, OR

(ii) is monotonic at and there exists one genotype such that in steady state, , and.

Assume (A3) and (A4) holds. Then in any steady state with, one must have.

PROOF―The frequency of the high allele at evolves according to

In steady state, we have that,

(10)

and

(11)

The term can be rewritten as follows:

That can be rewritten as:

This formula rests on the fact that all the genotypes such that can be deducted by applying the transform to all genotypes such that.

Furthermore, the allele independence property implies that for such that,

(12)

where is the total fraction of genotypes with among the offsprings of and.⁴ Note that one must have

(13)

Hence:

Now, if locus is selective, then is strictly increasing in. Consequently we have

(14)

This inequality rests on the fact that. It holds with a strict inequality unless all the but one are equal to zero.

We now show that unless or, there exists a pair of genotypes such that, , and (14) strictly holds. First note that if, there exists a genotype such that, and.⁵ Next, note that if there exists such that, the mixing property implies that for two parents of the same genotype, there is a positive probability of having an offpsring such that, for any between and. As long as and, there are more than two values of that satisfy that property. Consequently, there are at least two strictly positive values of, and one can take.

Thus, if, it must be that there exists a pair such that, , and (14) strictly holds.

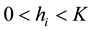
Alternatively, consider the case where is monotonic. Then (14) also holds. Furthermore, assume there exists such that, , and. Let. Then (14) will hold with strict inequality for, such that, , and. If,

taking and applying the mixing property to locus, generates both offsprings with and implying that and. If, the Lemma implies that. Taking and then generates both offsprings with and implying that and. Thus, we can again pick up a genotype and a pair such that, and (14) strictly holds.

From (14), we get that

(15)

Once again, there exists a pair such that, , and (15) strictly holds. The RHS can be rewritten

where the first step derives from (13) and the second one from (12).

Inequality (15) means that the fitness of the high alleles in the gene pool of the offsprings of and is higher than the average fitness of the offsprings as individuals, because those with more H-alleles at live longer. In order to get that, the allele invariance property is needed. Otherwise, it could be that the offsprings of, that have a high have a lower fitness than the others because they are systematically poorly endowed at other loci.

Going back to (11), we see that

(16)

where the strict inequality comes from the fact that for at least one pair such that.

We now have

(17)

where we have applied gene conservation and is defined as

Observe that can be rewritten as

Furthermore, one can write where. Iterating the monotonicity property, we find that is nonincreasing in, while does not depend on. We then have that

Since is monotonic, the term in brackets is nonpositive. Thus, the sum is nondecreasing in, while the last term is constant in. Therefore, the LHS is nondecreasing in, for any such that. Summing this property across these’s, we also find that is nondecreasing in. Roughly, that property means that the average mortality of offsprings improves when one parent is genetically enhanced at locus. The monotonicity property is needed to get that. Otherwise, it could be that parents with more H-alleles at, everything else equal, have an systematically biased toward high-mortality genotypes.

Let us now go back to (17), which we can rewrite

For a given, we have that, that increases with and that weakly increases with. Thus, once again, we have the following inequality:

Consequently,

where the steady-state condition (10) has been used to derive the first term.

By virtue of (16), (3) and (6), the last term in that formula must be equal to, so that. (16) then implies that, which is a contradiction. Hence, it must be that either or. Q.E.D.

The last set of inequalities tell us that since parents who have a greater have children with a higher fitness, these parents’ children tend to increase the survival rate of the high allele at relative to average. Since, in addition, the survival rate of the high allele at among their children is greater than their children’s average survival rate, these two effects together imply that the fitness of the high allele at is strictly higher than average. But that cannot be in steady state, unless or.

4. Autarky

We now describe how an individual’s genotype affects his/her productivity at various activities, depending on the ecomic setting.

The alleles present at a given locus determine the individual’s productivity at a corresponding activity denoted by the same index. This productivity is a strictly increasing function of, the number of H-alleles at locus. Any individual has a total time endowment equal to 1. The time allocation constraint of genotype is therefore given by

(18)

where is the individual’s output in activity.

Finally the individual’s fitness is

where is the individual’s consumption of activity, and is the “utility function”, which is concave in each argument, and satisfies the “Inada conditions”:,.

Under autarky, we have, and the following result holds:

PROPOSITION 2―Under autarky, all loci are selective. Therefore, in any steady state such that, , all individuals are of genotype, i.e. the H-allele is fixed at all locations.

Proof―Type has a more favorable time budget constraint than type. Therefore, it achieves a higher fitness. The rest follows from the previous subsection. Q.E.D.

Note that the case is not of interest: it means that the high allele does not exist at that locus.

5. Trade

Let us now look at the trade case. Each good is traded at price. We assume the following normalization for the price vector

(19)

People allocate their time between the various activities so as to maximize their income,

subject to the time allocation constraint (18). Their demand vector is the one which maximizes subject to their budget constraint:

Types with lower incomes must achieve lower fitness and therefore disappear in the long run.

Furthermore, must be monotonic at all loci. The reason is that the vector supplied by a geno- type can also be supplied by genotype. On the other hand, all loci need not be selective, as genotypes with fewer H-alleles at locus may achieve the same income as fitter genotypes, by just specializing.

Define a long-run equilibrium (LRE), as a stationary state such that the economy is in equilibrium, i.e. each genotype sets its supply and demand as just described, and markets clear for each good. The following proposition generalizes the results derived for the two-loci case in Saint-Paul (2007).

PROPOSITION 3―(i) In any LRE such that, , a given type only supplies goods corresponding to loci in their genotype where they have the highest number of -alleles:

(ii) In any LRE such that, the price vector is such that

(20)

(iii) In any LRE, there exists a locus such that, i.e. allele H is fixed at locus.

Proof of (i)―Iterating the mixing property with appropriately chosen parents, one can easily show that if, , in steady state there exists a strictly positive supply of genotypes with a arbitrary, strictly positive number of H-alleles at each locus. In particular, there exists a strictly positive mass of the best genotype. Next, note that if, then genotype achieves higher fitness than, and hence.

Assume there exists a genotype such that for such that Clearly, the plan achieves a strictly higher income level and is feasible (i.e. satisfies (18)) for. Consequently, , implying. But, given that is monotonic, Proposition 1, under assumption (ii), would then imply that, which makes it impossible for to exist. Consequently, any type only supplies goods where it has an -allele.

Proof of (ii)―The price vector defined by (20) is the one which makes type indifferent between all activities. Assume there exists an LRE with a different price vector. Then there exists a pair of goods such that

(21)

and since more income is yielded for type by offering good than good.

Since satisfies the Inada conditions, the demand for good is strictly positive; since does not

supply good, there exists such that and. By virtue of (i),. Further- more, , otherwise would prefer to supply instead of as well.

The income of type is. The supply vector is feasible for type, since is more productive than at all activities. The supply vector defined by, , , , also satisfies (18) for. Therefore,

where the last inequality comes from (21). But, this cannot hold since it again implies Consequently, there exists such that Furthermore, as,

iterating Lemma 1 implies that. Monotonicity of then implies that (ii) in Proposition 1 is satisfied. Consequently,. But that contradicts the requirement that. Q.E.D.

Proof of (iii)―Suppose not; then by iterating the mixing property with appropriately chosen parents, one can prove that. But that contradicts (i). Q.E.D.

The preceding proposition tells us what properties an LRE must necessarily have, but does not tell us whether an LRE exists and whether, as in the preceding analysis, one can construct equilibria with a positive level of some -alleles. We now establish a result which tells us that an LRE exists with a strictly positive proportion of L-alleles, provided these alleles are not too frequent.

To do so, for any subset of we define as is the set of all

genotypes such that their loci saturated with -alleles (which define the activities at which they can possibly specialize) are all in.

PROPOSITION 4―Let be the inverse demand function for the fitness maximization problem of an individual with income R facing price vector Let

Then there exists an LRE with a distribution of genotypes if and only if this distribution satisfies the following property:

(22)

Proof―We first prove that this condition is necessary. The RHS of (22) is the total time supplied by genotypes in (relative to the population's total time). Proposition 3, (i) implies that it must be allocated among goods such that, i.e. among goods in. It also implies that in any candidate equilibrium, income per

capita (equal to the income of any genotype) must be equal to Thus, is the per capita amount of good consumed and produced in any candidate equilibrium. The LHS of (22) is therefore the total time input needed to produce all the goods in. It must be greater than or equal to its RHS, since genotypes in cannot produce any other good. Otherwise, supply would exceed demand. Note that (22) applied to

implies that one -allele is fixed (the RHS is then the total supply of all genotypes such that). Also, (22) applied to boils down to Walras’ law, since it is equivalent to, and by Walras law.

Let us now prove sufficiency. In order to do so, we construct a set of functions, representing the share of time of genotype devoted to activity, such that:

(23)

(24)

(25)

⁶One can trivially check that such an allocation exists, since one -allele is fixed, all genotypes have at least one locus where.

If we are able to construct such functions, then this is indeed an equilibrium, since supply equals demand for all goods, and since the price vector in (20) implies that a genotype is indifferent between supplying all the goods at which it has -alleles.

To construct the, we use the following algorithm. We start from any arbitrary allocation satisfying (23) and (25). This defines the initial stage.⁶ Then we move from stage to stage as follows. At the beginning of stage, the set can be partitioned into three subsets:

That is, those goods for which supply equals demand, those for which there is excess demand, and those for which there is excess supply. Note that since, is empty if and only if is empty. If, then we have an equilibrium, and the algorithm stops.

Assume therefore that it is not the case. Then neither nor is empty. We now distinguish two cases.

Case A. Assume there exists a partition of such that

and:

(P)

That is, people who do produce goods in cannot produce goods in.

For any good, let

Clearly, one has, for all. We then have

This strict inequality comes from the fact that and from the fact that is non-empty.

Furthermore,

This is because if and, then, implying. Therefore .

Interverting, we get

Now, note that, ,: if I produce one good in, all my loci with -alleles are also in. Consequently,

which clearly violates assumption (22). Case A is therefore ruled out.

Case B. Assume then that there exists no such partition. We can construct a chain of goods such that the following property holds:

PROPERTY Q:

(a)

(b)

(c), for

(d), , and

To construct such a chain, proceed as follows. We will write if (,and). In this case, we call the set of genotypes that satisfy this property:. Property (d) implies that the chain we want to construct is such that

Start from a set. As property (P) is violated, there exists, , such that

If, stop the procedure there, and take.

If not, then. Add to:. Since, it must be that,. Use again the fact that (P) is violated. There exists, , such that. Given that either or, there exists a chain of length, such that, , , and. If, we use that chain and stop the procedure. Otherwise, we add to, and iterate again.

More generally, at each iteration, there is a set such that, and such that for all, there exists a chain such that, , and (The chain property) Because (P) is violated, there exists and, such that. Let be the chain corresponding to. If, we use the chain and stop the procedure. If, we use and iterate the procedure. As the new member is connected to via the chain, still satisfies the chain property. As, it also satisfies. As the number of elements in goes up by one unit at each iteration, one must find an in a finite number of iterations.

Next, we can use such a chain to construct a new allocation of labor for stage. Let

and

Define the new allocation as follows:

The new allocation clearly still satisfies (23) (as), and (25) (as ). Futhermore, one has, as. Finally, for,. Hence, all markets that were in equilibrium remain so. Furthermore, as, market weakly remains in excess supply, and similarly market weakly remains in excess demand. Therefore:

Finally, we note that either

(i)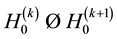, which will be true provided or . In such cases the new allocation restores equilibrium in market (resp.).

(ii) Or, the chain and its associated chain of genotypes no longer satisfy Q; that is the case if for some, in which case. In such a case, we have constructed a new allocation such that has increased by at least one unit, and which satisfies (23) and (25).

Thus, at each stage, the quantity strictly increases. As it is bounded, the proce- dure cannot go on forever, and the only case in which one cannot iterate it is if. This proves

the existence of equilibrium. Q.E.D.

Clearly, conditions (22) are pretty stringent, so that it is not straightforward to construct an equilibrium.

However for close enough to 1, i.e. small enough when, they are clearly satisfied, since appears on the RHS only for, in which case (22) is always satisfied with equality, due to Walras’ law:. Therefore there always exist equilibria with a strictly positive fraction of genotypes with -alleles, provided this fraction is small enough.

Note that the greater the number of loci, the greater the number of conditions that must hold. Intuitively, it suggests that the equilibrium fraction of -alleles must become smaller. Intuitively, if the initial distribution of alleles in the population is such that (22) is violated, we expect a number of H-alleles to eventually become fixed, which is equivalent to a reduction in. The process would continue until is small enough for the number of relevant activities not to be too large, so that (22) holds.

References

NOTES

¹In this line of work, grouyp selection often plays an important role. See for example Cavalli-Sforza and Feldman [1] ; Lumsden and Wilson [2] ; Gintis [3] , Boyd and Richerson [4] .

²Interesting surveys on interactions between the economic and biological spheres include Hirshleifer [5] , Robson [6] , and Seabright [7] .

³I addition to this, the most closely related paper is Horan et al. [9] . A related literature (see Hammerstein [10] , and in particular Bowles and Hammerstein [11] ), studies the rise of markets and specialization in animal societies, but does not draw this paper’s implications for the gene pool.

⁴If, we can write down the same steps using the smallest value of such that as a benchmark.

⁵The only other possibility is to only have genotypes such and such that, but random mating and mixing imply that they will produce offsprings such that.