Natural Science
Vol.6 No.10(2014), Article
ID:46944,6
pages
DOI:10.4236/ns.2014.610068
Nose and Sinus Air Flow Model
R. De Luca1, M. Gamerra2, G. Sorrentino2, E. Cantone3,4
1Department of Physics "E. R. Caianiello", University of Salerno, Fisciano, Italy
2Divisione di Otorinolaringoiatria, Ospedale “S. Leonardo”-A.S.L. NA 3 sud, Castellammare di Stabia, Italy
3Department of Neuroscience, Reproductive and Odontostomatologic Science, ENT Unit, “Federico II” University, Naples, Italy
4Department of Molecular Medicine and Medical Biotechnology, “Federico II” University, Naples, Italy
Email: rdeluca@unisa.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2014; revised 10 May 2014; accepted 17 May 2014
ABSTRACT
Air flow in nose and sinuses is studied by means of a simple model based on the steady-state ideal fluid flow assumption and repeated use of Bernoulli’s equation. In particular, by describing flow of air drawn in through the vestibulumnasi during inspiration, we investigate how ventilation of the maxillary sinus is affected by surgical removal of part of the lateral walls of the nasal cavity close to the ostiummeatal complex. We find that, according to the model proposed, removal of tissues from this inner part of the nasal cavity may cause a decrease of the flux rate from the maxillary sinus.
Keywords:Air Flow Model, Nose and Sinus, Bernoulli's Equation

1. Introduction
The human ventilation system works by means of gaseous exchanges, which takes place between the nose and sinus cavities, and between the latter and the blood circle through the mucosa [1] . During respiratory acts, air flowing in the nasal cavity reaches the paranasal sinuses through the hosts and their ducts [2] . Therefore, a correct anatomical and physiological equilibrium which is able to generate effective pressure gradients inside the nasal cavity plays an important role in the ventilation of the sinus cavities. During a single inhalation, air flows from the vestibulum towards the coana and produces, by “sucking effect”, negative pressures into the ostiummetal complex [3] . As a result, at the beginning of each nasal inhalation action, a negative nose pressure is generated, in such a way that air flows out from the sinus cavities, due to the effect of aspiration. Air successively re-enters these cavities when the inspiration phase ends, and thus one of the continuous life-long respiratory cycles is completed. A fundamental role for a correct ventilation is thus played by the anatomical conformation of the ostiummeatal complex [4] .
In sinus physiology, air exchange is also regulated by diffusive molecular mechanisms related to the chemical and physical characteristics of the inhaled air mixture. The correct and continuous sinus ventilation due to the physical phenomenon described above is the reason why air in the sinus cavities is always in motion. The shape of the nasal cavity can be assimilated to that of a tube to which, under stationary conditions and ideal fluid flow, Bernoulli’s equation can be applied. Under the hypothesis of applicability of Bernoulli’s equation, therefore, the single particles of the fluid are taken to describe laminar trajectories with no energy loss in all ducts.
In the present work, the problem of air flow through the ostiummeatal complex coming from the maxillary sinus is studied by means of repeated use of Bernoulli’s equation. The work is thus organized as follows. In the following section, we give a detailed description of the model adopted. In the third section, we solve the model equations by means of a first-order perturbation approach, deriving a direct analytic dependence between the flux rate in the infundibulum and the nose’s effective section. Conclusions are drawn in the last.
2. The Model
We consider the schematic model of the ostium-meatal complex reported in Figure 1. In this figure we schematize the maxillary sinus as a spherical cavity (M), in which air at the atmospheric pressure is present. The ostiummeatal complex is seen as a short duct linking the nasal cavity (N) to the maxillary sinus. In the schematic representation of Figure 1, during inspiration air enters the nose through the vestibulumnasi and comes out through the coana (C-posterior). This air-flow produces a depression in N close to the ostiummeatal complex, sucking air from the maxillary sinus.
By denoting with S0 and S1 the effective sections of the inner and outer portions of the nasal cavity, respectively, and by S2 the effective section of the ostiummeatal complex, we assume that air behaves as an ideal fluid [5] through these cavities. Air flows with velocities V0, V1, and V2 through the correspondingly indexed sections, so that, by continuity equation we can write the following relations for the flow rates in these sections:
 . (1)
. (1)
By extending Bernoulli’s equation to a Y-shaped tube [6] , in the absence of gravitational effects, we may write:
 . (2)
. (2)
where p0 and p1 are the pressures in the inner and outer portions of the nasal cavity, respectively, and p2 is the

Figure 1. A schematic representation of the ostium-meatal complex. Air, drawn trough the vestibulim nasi, enters the nasal cavity (N) with velocity V1. Air fromthe ostium-meatal complex, having velocity V2, mixes with inhaled air in the inner nasal cavity towards the coana (C) during inspiration. Air from the maxillary sinus (M) is assumed to be at rest at atmosperic pressure pa.
pressure in the ostiummeatal complex. Moreover, in Equation (2) ρ is the density of air, Δτ1 is the volume of the inhaled air, Δτ2 is the volume of air drawn from the ostiummeatal complex and Δτ0 is the volume of air flowing in the coana, given by:
 . (3)
. (3)
Notice that Equation (3) is a mere consequence of Equation (1). In this way, Equation (2) can be rewritten in terms of the volume flow rates, defined in Equation (1), as follows:
 (4)
(4)
By Bernoulli’s equation, considering a point in M and a point in the ostiummeatal complex, we can write
 (5)
(5)
where pa is the atmospheric pressure. Moreover, by assuming that air flowing in the vestibulumnasi is drawn at constant velocity VL during inspiration, we have:
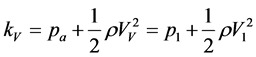 (6a)
(6a)
 . (6b)
. (6b)
where kV is a constant and SV is the effective section of the vestibulumnasi. In this respect, we need to specify that the assumption on VV is correlated to the patient’s needs of air intake, which can safely be assumed to be constant. On the other hand, the value of kV is the sum of the atmospheric pressure and of the dynamical pressure term linked to VV. This term, though varying from individual to individual, remains constant for a single patient. By now considering Equations (5) and (6a-b), we may rewrite Equation (4) in the following way:
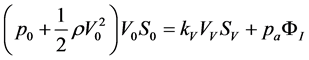 , (7)
, (7)
where ΦI = S2V2 is the flux rate inside the ostiummeatal complex. By implicitly differentiating Equation (7) and by noticing that, by Equations (1) and (6b), dΦI = d(S0V0), we write:
 (8)
(8)
where the differential quantity dΦI accounts for an infinitesimal variation of the flux rate in the ostiummeatal complex solely due to a corresponding infinitesimal variation S0 of the coana effective section. In order to obtain a set of equations by which we can directly relate dΦI with dS0, we introduce one further assumption, i.e., that air can flow at the same temperature inside the nasal cavity before and after the variation dS0 has taken place, so that:
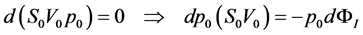 (9)
(9)
By now substituting the above expression in Equation (8) we have:
 . (10)
. (10)
We notice that in Equation (10) dV0 can be related to dS0 by equating the expression dΦI = d(S0V0), following from Equations (1) and (6b), to the expression for dΦI obtained from Equation (10). In this way, we have:
 . (11)
. (11)
By considering Equation (11), it is now not difficult to show that an implicit functional relation of V0 in terms of S0 is given by the following expression:
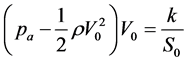 . (12)
. (12)
where k is a constant parameter referring to a specific group of patients. In order to obtain a meaningful order of magnitude for k, we might consider the main term in Equation (12), namely, the product paV0S0. In this way, we notice that, for V0 ≈ 5.0 cm/s and for S0 ≈ 100 mm2, we have k of about 5.0 N∙m∙s−1. Equation (12) can now be inverted either numerically, either analytically, in order to obtain V0 vs. S0 curves, which we show in Figure 2 for various values of the constant parameter k. Considering now Equations (10) and (11), we can set:
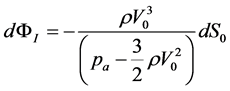 , (13)
, (13)
which directly relates the infinitesimal change dΦI to dS0. By means of Equation (12) it could be possible to find how the flux rate ΦI depends explicitly on S0. However, in the following section, we shall adopt a perturbation approach to obtain this dependence.
3. Perturbation Solution and Approximated Results
In the previous section we have obtained Equations (12) and (13), which represent the solution to the proposed problem of finding how the flux rate ΦI inside the ostiummeatal complex varies with respect to the effective area of the coana S0. Even though an analytic expression for such dependence can in principle be found, it is not convenient to proceed in this way, since a perturbation approach can be adopted, given that the dynamic pressure ρV02/2 is, for this type of system, much smaller than pa. With this in mind, to first order in the term ρV02/2pa, Equations (12) and (13) can be written in the following way:
 , (14a)
, (14a)
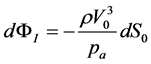 . (14b)
. (14b)
Solving for V0 in Equation (14a), we have:
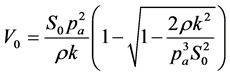 , (15)
, (15)

Figure 2. The velocity V0 of air in the inner part of the nasal cavity as a function of the effective area S0 for ρ = 1.29 kg∙m−3, pa = 1.0 atm and for the following values of the parameter k (from bottom to top): 6, 7, 8, 9 N∙m∙s−1.
In this expression we chose the minus sign in front of the square root, since it correctly gives a decreasing behavior of V0 for small values of S0 and take S02 > 2ρk2/pa3. In Figure 2, we show the velocity V0 of air in the inner part of the nasal cavity as a function of the effective area S0, as given by Equation (15), for ρ = 1.29 kg∙m−3, pa = 1.0 atm, and the following values of the parameter k (from bottom to top): 6, 7, 8, 9 N∙m∙s−1.
Substituting now Equation (15) in Equation (14), we finally have:
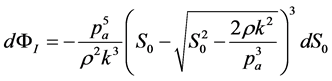 , (16)
, (16)
By now calling A = pa5/ρ2∙k3 and B = 2 ρk2/pa3, we may easily integrate Equation (16), obtaining
 , (17)
, (17)
where c is a constant. Since we are only interested in finite variations of ΦI, we do not need to calculate the constant c. Moreover, we make take Equation (16) as the first-order approximation of the flux rate variation ΔΦI due to a finite variation of the nasal cavity effective section ΔS0, so that
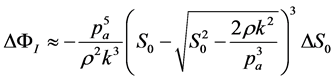 (18)
(18)
The above equation can be considered as an approximation to the solution to the problem we considered in the present work. For some typical values of the parameters in Equation (18) and for an effective section of about one tenth of a square centimeter, the coefficient linking ΔΦI and ΔS0 is found to be numerically equal to 8.6 × 10−3 m∙s−1. In this way, by taking, for example, ΔS0 = 1.0 mm2, we have ΔΦI = −8.6 mm3∙s−1. The derivative dΦI/dS0, as it can be obtained from Equation (16), is represented, as a function of S0, in Figure 3 for ρ = 1.29 kg∙m−3, pa = 1.0 atm, and for the following values of the parameter k (from top to bottom): 6, 7, 8, 9 N∙m∙s−1. From Figure 3 and from Equation (18) it can be seen that the derivative dΦI/dS0 is negative, so that any positive variation of S0 causes a decrease of the flux rate in the ostiummeatal complex. In this respect, one might argue that surgical removal of anatomical structures close to the ostiummeatal complex might worsen the ventilation functional efficacy of the maxillary sinus. This particular aspect has been already observed when analyzing the effectiveness of sinus ventilation with the aid of nose and sinus manometric measurements [7] . In these particular studies it was found that better functional results can be achieved by using a conservative surgical technique preserving nose anatomy rather than a non-conservative endoscopic surgery.
4. Conclusion
Air flow in the nasal cavity is studied by means of a simple model resting on the stationary ideal fluid flow hy-
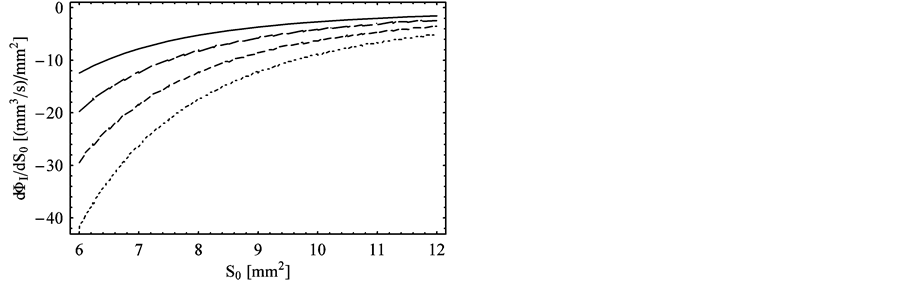
Figure 3. The derivative dΦI/dS0 represented as a fiunction of S0 for ρ = 1.29 kg∙m−3, pa = 1.0 atm and for the following values of the parameter k (from top to bottom): 6, 7, 8, 9 N∙m∙s−1. The units of the derivative are purposely expressed as “(mm3/s)/mm2” instead of “mm/s”.
pothesis. Under these assumptions, Bernoulli’s equation can be used. The model might thus be used to give an elementary description of nose and sinus ventilation. Under these simplifying assumptions, the present analysis predicts that the flow rate of air sucked from the maxillary sinus towards the nasal cavity decreases as the area close to the ostiummeatal complex increases. In this respect, one might argue that surgical removal of anatomical structures close to the ostiummeatal complex may worsen the ventilation functional efficacy of maxillary sinus, in accordance with experimental observations.
References
- Stammberger, H. and Hawke, M. (1993) Essential of Functional Endoscopic Sinus Surgery. Mosby, St. Louis.
- Messerklinger, W. (1978) Endoscopy of the Nose. Urban & Schwarzenberg, Baltimore.
- Passali, D. (2003) Le rinosinusiti. Pacini Ed., Pisa.
- Bruno, R., Gamerra, M., Porpora, D., Pagano, G., Napolitano, B. and Bruno, E. (2004) Nose: Aesthetics and Function. Anales Otorrinolaringológicos Ibero-Americanos, 31, 307-323.
- Halliday, D., Resnick, R. and Walker, J. (2001) Foundamentals of Physics. 5th Edition, John Wiley & Sons, New York.
- Gamerra, M. and De Luca, R. (2004) Un modello semplice per descrivere gli effetti sulla ventilazione sinusale del flusso d’aria immessa nella cavità nasale. Giornale di Fisica, XLV, 225-228.
- Gamerra, M., De Luca, R., Pagano, G., Merone, M. and Cassano, M. (2013) The Nose and Sinus Manometry: A Biophysical Model Applied to Functional Endoscopic Sinus Surgery. Journal of Biological Regulators and Homeostatic Agents, 27, 1021-1027.

