Natural Science
Vol.5 No.6(2013), Article ID:32838,5 pages DOI:10.4236/ns.2013.56082
The fundamental reasons for global catastrophes
![]()
1The Volgograd Branch of Moscow Humanitarian-Economics Institute, Volgograd, Russia; shavi2011@yandex.ru
2The Volgograd State Technical University, Volgograd, Russia
Copyright © 2013 Viktor I. Shapovalov, Nickolay V. Kazakov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 4 April 2013; revised 5 May 2013; accepted 13 May 2013
Keywords: Self-Organization; Entropy; Entrostat; Global Catastrophes
ABSTRACT
This paper uses a new statistical method for studying self-organization in order to explain the origins of global catastrophes, namely the exceeding of the critical level of the planet’s organization. This method differs from traditional methods, because it uses specific notions such as the “entrostat” and “critical level of the organization of the open system”.
1. INTRODUCTION
A worsening of our relations with nature has been observed over the past 30 years. Let us emphasise the main idea: natural disasters, weather anomalies, ecological crises, technical catastrophes, and military conflicts have a common factor, namely disorder increase, i.e. growth in environment entropy. In modern science, numerous above disaster types are studied separately, because no fundamental theory unites them in a general trend. In this paper, we show that it is possible to determine the fundamental reasons for this trend using a new approach to explore the self-organization of open systems [1-6]. We understand the reasons determined by the first principles as the fundamental reasons. In case of our paper, we refer the law of increase of entropy to first principles.
The introduction of the terms “entrostat” and “critical level” of the system’s organization is specific to this approach. The application of this approach to the system of the “Earth” has allowed us to identify the fundamental cause of the emergence of global catastrophes, namely the exceeding of the critical level of the planet’s order. In our paper, we understand as Global Catastrophes, firstly, world nuclear war, and secondly, large-scale technical and natural calamities threatening to human extinction, but which are not caused by external influence to the Earth. In our opinion, this new approach creates a new scientific trend for controlling the surrounding world [7].
Since the middle of the last century, two main directions of self-organization study have been formed: the entropy approach in statistical physics [8,9] and the methods of nonlinear dynamics [10,11]. In statistical physics, owing to the works of Boltzmann, entropy is defined as a quantitative measure of disorder. In recent decades, a crisis in statistical physics has questioned this interpretation of entropy [12,13]. The main argument of the opponents of this interpretation is that statistical physics has not offered a successful explanation of the phenomenon of self-organization.
The main obstacle to describing self-organization in statistical theory is the difficulty of comparing the entropies of different states of an open system. By introducing the concept of the entrostat, we make it possible to look upon this problem of the comparison of various entropies from a new viewpoint. As a result, the study of self-organization within statistical theory has finally made headway.
2. STATISTICAL CRITERION OF ENTROPY CHANGE IN AN OPEN SYSTEM
The notion of the entrostat with reference to open systems was first introduced by [1,14] and further developed in [2,6,15]. We term a system that does not change its entropy while interacting with the system under study the entrostat. In practice, if the entropy change of the external environment can be neglected in comparison to the entropy change in the system under study, then the given external environment acts as an entrostat.
For example, in heat conduction tasks, the thermostat is the entrostat. Moreover, although loud noise created by traffic outside an open window would force us to close the window, the traffic (i.e. the entrostat) would not even notice this action. It is also well known that it is easier to follow bureaucratic regulations than it is to procure their cancellation, i.e., the laws of society are the rules that one person interacting with society (i.e. the entrostat) is unable to change. Such examples are numerous.
According to the authors’ opinion, the phenomenon of the entrostat arises when the studied system’s activity upon the entrostat is so small that it may be compared with the chaotic structural noise in the entrostat (i.e., it is infinitely small in relation to the entrostat). Using the notion of the entrostat in open systems allows us to propose a new approach to study self-organisation phenomena. The advantage of the entrostat from a theoretical standpoint is that it allows us to replace the external environment with a selected constant parameter in order to characterise the intensity of the external influence under study. This parameter is termed the degree of system openness and is marked as a [1].
The strict mathematical background of this approach was presented in [2-4] and reviewed in [6]. Using this approach, the existence of the critical level of the system’s organisation 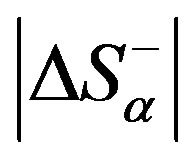 1 has been proven for systems under the influence of the entrostat (see 5th Section). In terms of the system organisation, we thus understand its structural links.
1 has been proven for systems under the influence of the entrostat (see 5th Section). In terms of the system organisation, we thus understand its structural links.
As shown in [1,6], the critical level of organisation has the following specifications:
1) If the system is organised below its critical level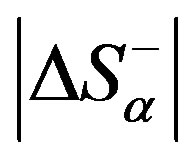 , the processes of ordering and self-organisation would prevail in it, increasing the order in the system up to
, the processes of ordering and self-organisation would prevail in it, increasing the order in the system up to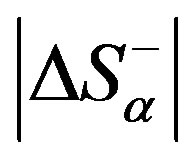 ;
;
2) If the system is organised above its critical level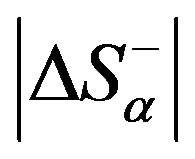 , the processes of disorganisation would prevail in it, reducing the order to
, the processes of disorganisation would prevail in it, reducing the order to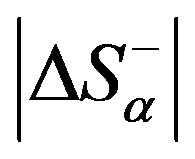 ;
;
3) At the critical level, the given processes balance out and the system’s state becomes stationary.
These three proposals represent the statistical criteria of entropy change (SCEC) in the system under the influence of the entrostat.
Another important proposal of the new approach was also presented in [1,6]:
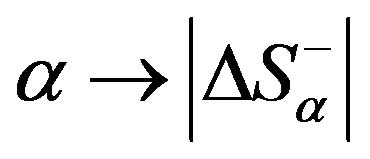 , (1)
, (1)
i.e., the value of the critical level of the organisation corresponds uniquely to the degree of system openness.
The obvious corollary of Eq.1 is the following conclusion:
In order to increase or decrease the critical level of the system organisation 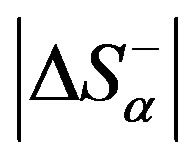 it is necessary to increase or decrease its degree of openness a.2
it is necessary to increase or decrease its degree of openness a.2
The proposals of the examined theory have a wide range of application in various fields of natural science [2,6,16]. One important application of this theory is discussed in the following section.
3. THE QUESTION OF FORMING GLOBAL TRENDS
The SCEC opens up a new direction for the study of global trends, including global catastrophes [1,5,17]. The transforming of nature by humankind either increases or decreases the order in it, namely changes the entropy of the environment. A question thus arises about the net change of entropy: is it more or less than zero? The conclusions presented in the previous section provide a definitive answer. A relatively constant degree of system openness (Earth) in relation to the spaceentrostat sets a certain critical level of its organisation  (see Eq.1). According to the SCEC (see Points 1 and 2), the processes of ordering and self-organisation will prevail on Earth below the critical level, while the processes of increasing disorder will prevail above the critical level. In the first case, humankind, by transforming the world around it, tends to increase order rather than disorder. This will endure until humankind exceeds the critical level of the organisation on the planet in the process of creation.
(see Eq.1). According to the SCEC (see Points 1 and 2), the processes of ordering and self-organisation will prevail on Earth below the critical level, while the processes of increasing disorder will prevail above the critical level. In the first case, humankind, by transforming the world around it, tends to increase order rather than disorder. This will endure until humankind exceeds the critical level of the organisation on the planet in the process of creation.
Above the critical level of the Earth, the processes that destroy the excess of its organisation are formed in it. Although these processes may be different in nature, the common factor that unites them is the increase in the disorder on the planet.
What is the action mechanism of entropy laws? Let us remind ourselves according to the well-known Boltzmann-Gibbs formula
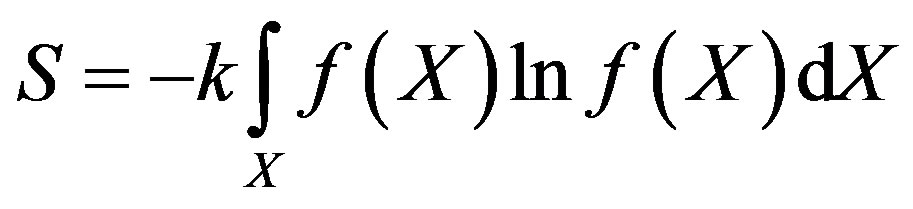
where k-const, X characterises the state of the system (Xstatistical variable), and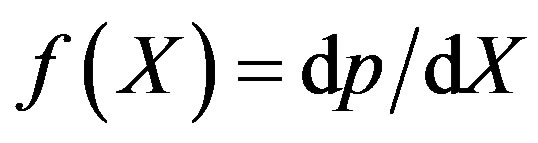 , entropy S, and probability p are interrelated. Hence, entropy laws increase the probability of contributing events to them and thus such events occur more often. The latter means that entropy laws generate the emergence of trends.
, entropy S, and probability p are interrelated. Hence, entropy laws increase the probability of contributing events to them and thus such events occur more often. The latter means that entropy laws generate the emergence of trends.
Thus, if the Earth’s critical level of organisation were exceeded, the probability of any destruction events would increase. For example, 1) the intensity of natural calamities (such as earthquakes, floods, and so on) ought to rise; 2) climate changes ought to create destructive weather anomalies; 3) the probability of technical catastrophes would increase; and 4) the probability of local and world wars would increase [5,17].
How can we find out whether the Earth has exceeded its critical level at the present time? The main symptom would be a trend towards increasing the intensity of those events that create disorder. According to the Centre for Research on the Epidemiology of Disasters (CRED), this trend has presumably been observed (Figure 1) [18].
In our opinion, statistical data by CRED indirectly confirm the fact that, probably, the destructive tendency prevails on the Earth now. We call specialists in field of collecting and analysis of statistical data to consider all destructive events on the Earth (including the destructions made by people—for example, as a result of the military conflicts, etc.) as one trend. The last is necessary because any destructions increase entropy and, as a result, they have to obey laws described in the 2nd section.
4. CONCLUSIONS
In the present paper:
• the new mechanism of destructive tendency occurrence on a planet is described;
• it is shown that this mechanism is the consequence of recently open entropy regularities;
• the conclusion is proved that the destructive tendency can lead to a Global Catastrophe;
• the way is specified, allowing do not suppose this Global Catastrophe.
In our opinion, creative activity of Humankind reduces entropy of environment (if organisation level of the Earth is below critical value). This entropy reducing brings the Earth near to its critical level of the organization. When there is an excess of this level on the Earth then the probability of any increasing entropy (disorder) events raises, i.e. the tendency of prevailing destruction (see 3rd section of our paper) is forming. This tendency can end only when sum of destruction will destroy excess of the organization of a planet. The most effective processes for this purpose are internal (i.e. Terrestrial) Global Catastrophes, including the most effective process—nuclear world war. The sole way to avoid these Catastrophes is to increase critical level of the organization of the Earth. According to the Eq.1, there is only one way for this purpose—to increase openness of a planet in relation to space.
Increasing the Earth’s openness (e.g., as a result of the large-scale development of the planets around the Earth, for example, the Moon, the Mars and so on) would increase the critical level. Thus, the processes of ordering and self-organisation would prevail; in other words, the probability of the events that contribute to creation would increase. This chain of events results a strong weakening of destruction trend in all manifestations.
The intensive development of the Moon (the nearest commensurate object to the Earth) could only be realised by the joint efforts of many states. Consequently, states would unite instead of war. On the contrary, if humankind refrains from such large-scale unlocking, the threat of general destruction reappears. This strategy would ensure humankind’s survival.
5. APPENDIX: CONCEPT OF THE CRITICAL LEVEL OF THE SYSTEM’S ORGANISATION
The inequality is known as [19,20].
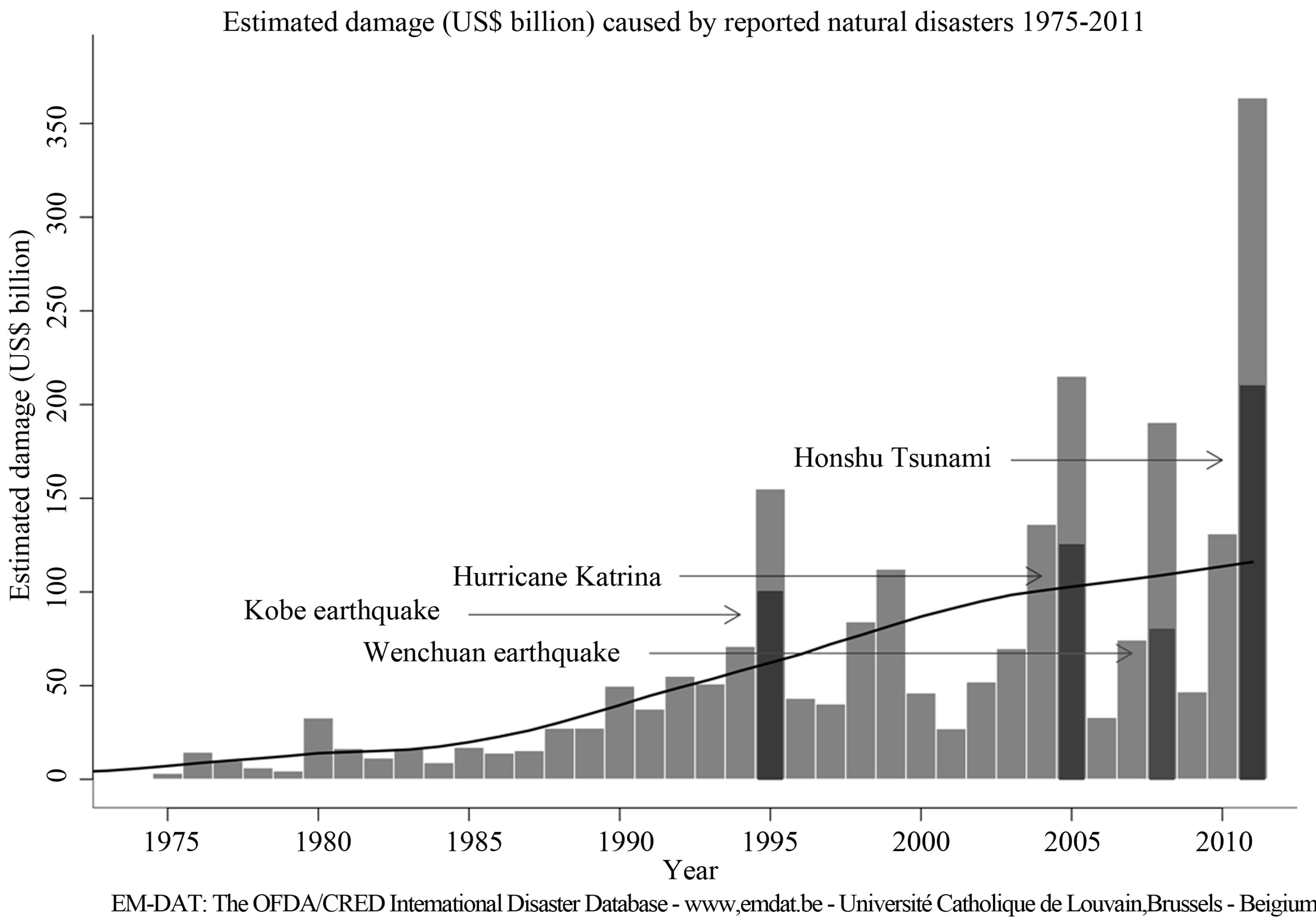
Figure 1. The almost monotonous damage increase indicates the existence of a destructive trend [18].
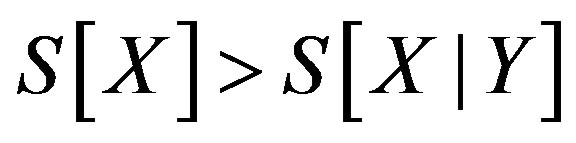 , (2)
, (2)
where S represents entropy; X and Y are the variables of a system; and 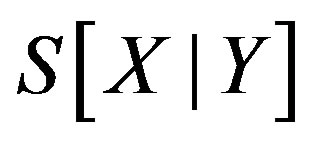 is the conditional entropy that describes the uncertainty of the determination of X under the condition that Y is given.
is the conditional entropy that describes the uncertainty of the determination of X under the condition that Y is given.
Let us term the main defect of an inequality Eq.2, which calls into question its practical use: according to Eq.2, entropy cannot increase after opening. However, if we apply this rule to the known task of the thermal contact of two bodies (e.g., they form an isolated system together), we find a contradiction, because entropy is necessarily increased at least in one body after the contact (opening). As shown in [3,4,6,15], the named defect is absent if the system is found to be under the influence of the entrostat.
The main advantage of introducing the concept of the entrostat is that it excludes the external environment when studying the behaviour of an open system. In particular, all the changes that occur during the interaction between the system and the entrostat relate to the system. Therefore, all new variables that describe these changes also relate to the system. For a system under the influence of the entrostat, the following relation has been proven [2,4,6]:
 , (3)
, (3)
where X characterises the state of the system;  is the entropy of the equilibrium state of the closed system;
is the entropy of the equilibrium state of the closed system; 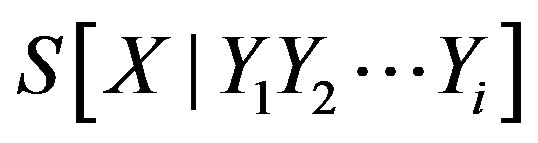 is the conditional entropy of the i-th stationary state of an open system found under the influence of the entrostat; and
is the conditional entropy of the i-th stationary state of an open system found under the influence of the entrostat; and 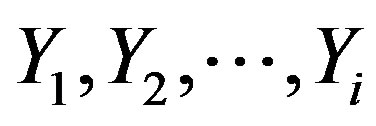 are the variables that describe the changes in the system that arise due to the influence of the entrostat.
are the variables that describe the changes in the system that arise due to the influence of the entrostat.
Note that the expression 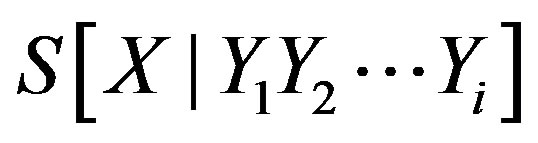 characterises the system’s entropy only if it interacts with the entrostat! Otherwise, it would be necessary, in addition to the variables
characterises the system’s entropy only if it interacts with the entrostat! Otherwise, it would be necessary, in addition to the variables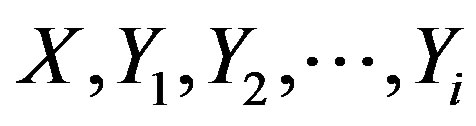 , to take into account those variables that describe the changes in all systems that presumably interact with the system under study. The latter is impossible to ascertain in most cases. Thus, in Eq.3 the comparison of the open states of the system is correct in terms of interaction with the entrostat.
, to take into account those variables that describe the changes in all systems that presumably interact with the system under study. The latter is impossible to ascertain in most cases. Thus, in Eq.3 the comparison of the open states of the system is correct in terms of interaction with the entrostat.
We term parameter a, which characterises the value of all the structural changes that have occurred in the system as a result of the influence of the entrostat on it, the degree of openness [1,2].
In Eq.3, for the leftmost position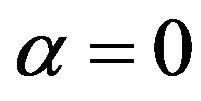 , which means an absolutely closed state; by contrast, for the extreme right position
, which means an absolutely closed state; by contrast, for the extreme right position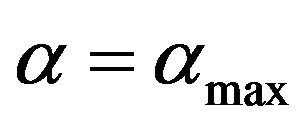 , which means a maximally open state. Let us denote the entropy value in the i-th stationary state with a degree of openness
, which means a maximally open state. Let us denote the entropy value in the i-th stationary state with a degree of openness 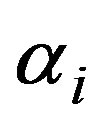 as
as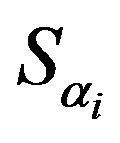 . Then, Eq.3 can be rewritten as follows:
. Then, Eq.3 can be rewritten as follows:
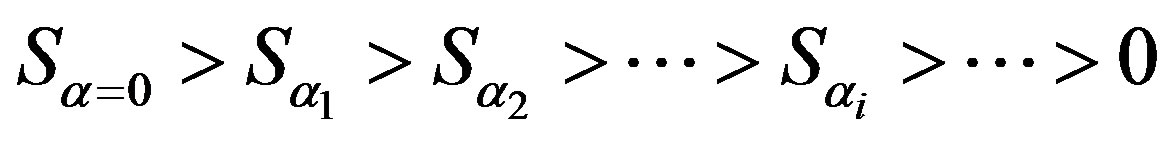
Graphically, this inequality can be expressed as the entropy range (Figure 2). In this figure,  represents the value of the system’s entropy at the beginning of certain processes and
represents the value of the system’s entropy at the beginning of certain processes and 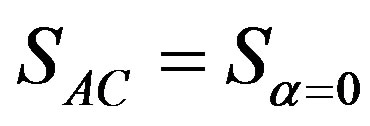 is the entropy value at the end of these processes in an absolutely closed state
is the entropy value at the end of these processes in an absolutely closed state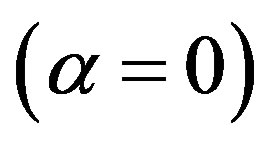 .
.
We also use the following designations (see Figure 2): 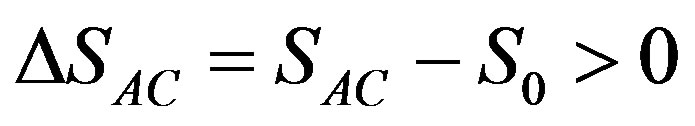 represents entropy change in an absolutely closed system that has reached equilibrium;
represents entropy change in an absolutely closed system that has reached equilibrium; 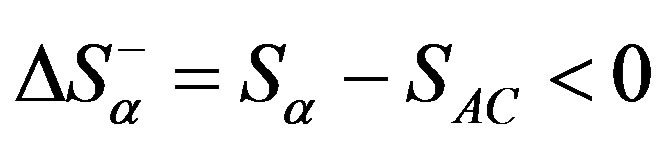 is negative entropy change by which the stationary value
is negative entropy change by which the stationary value 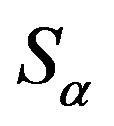 decreases with an increase in a; and
decreases with an increase in a; and 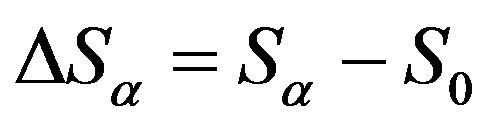 is entropy change in a system that has reached a stationary state and has a degree of openness a. It is thus easy to see that [1]
is entropy change in a system that has reached a stationary state and has a degree of openness a. It is thus easy to see that [1]
 . (4)
. (4)
Eq.4 differs from the known one [21]:
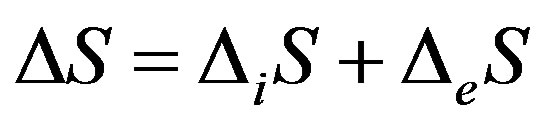 where
where 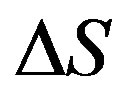 is the system’s entropy change;
is the system’s entropy change; 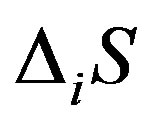 is the entropy change produced inside the system; and
is the entropy change produced inside the system; and 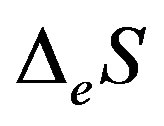 is the outflow or inflow of entropy in the system from the outside. Indeed, according to [21],
is the outflow or inflow of entropy in the system from the outside. Indeed, according to [21],  may be positive as well as negative, whereas
may be positive as well as negative, whereas 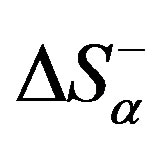 is always less than zero.
is always less than zero.
Eq.4 is the mathematical expression of the following evidence: all the irreversible processes in the system are divided into processes that either increase or reduce entropy. Thus, 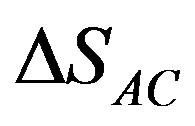 is the contribution of those processes that increase entropy, whereas
is the contribution of those processes that increase entropy, whereas 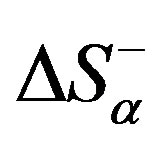 is the contribution of those processes that reduce it. The latter allows us to consider
is the contribution of those processes that reduce it. The latter allows us to consider 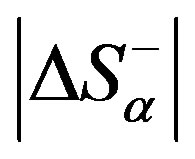 as a measure of the organisation of the
as a measure of the organisation of the
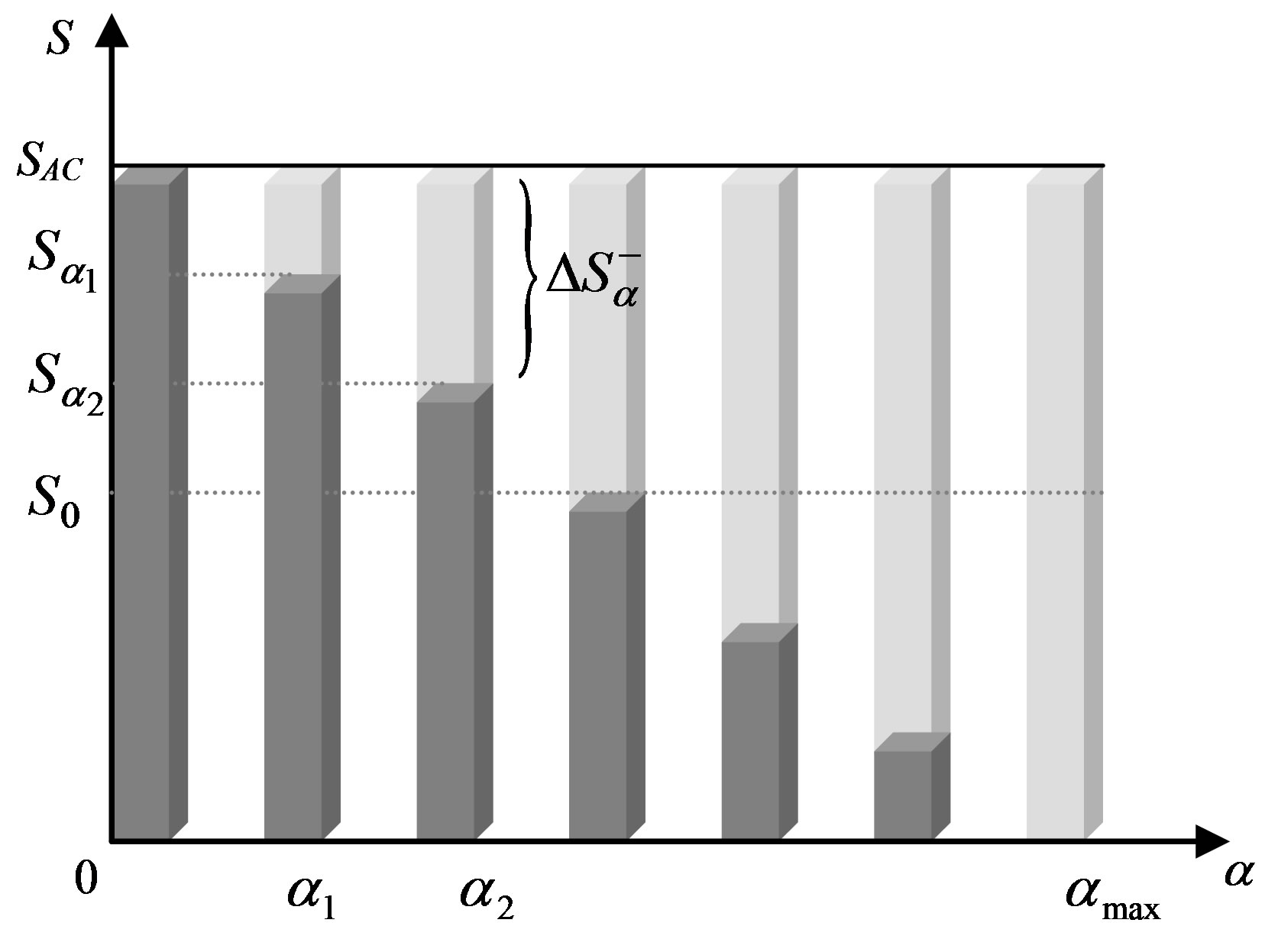
Figure 2. Qualitative picture of the entropy range of the system. The values of entropy S for the stationary states of the system are shown at different degrees of openness a [1]. The shaded part of the column quailtatively shows the entropy value of the system at the stationary state at a certain degree of openness.
system at a stationary state. According to Eq.3, by the organisation of a system we understand the structural connections described by the variables 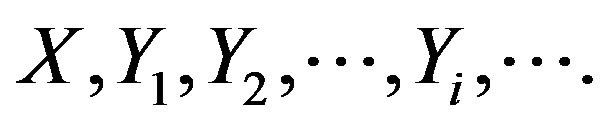
According to [1,4,6], if the system is organised below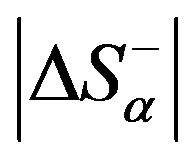 , the processes that increase order would prevail in it, whereas if the system is organised above
, the processes that increase order would prevail in it, whereas if the system is organised above , the processes that reduce order would prevail in it. Consequently,
, the processes that reduce order would prevail in it. Consequently, 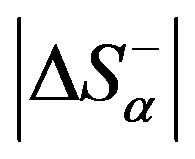 plays the role of a criterion. Therefore, the value
plays the role of a criterion. Therefore, the value 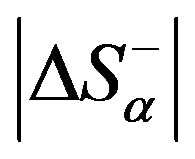 is termed the critical level of the system’s organisation.
is termed the critical level of the system’s organisation.
REFERENCES
- Shapovalov, V.I. (1995) Entropiyny mir (The entropy world). Peremena, Volgograd.
- Shapovalov, V.I. (2001) Formation of system properties and statistical approach. Automation and Remote Control, 62, 909-918.
- Shapovalov, V.I. (2004) To the question on criteria of order change in open system: The statistical approach. Applied Physics, 5, 25-33.
- Shapovalov, V.I. (2008) The criteria of order change in open system: The statistical approach. arXiv:0801.2126v1
- Shapovalov, V.I. (2008) Entropy oscillations. arXiv:0812.4031v1
- Shapovalov, V.I. (2012) The criterion of ordering and selforganization of open system. Entropy oscillations in linear and nonlinear processes. International Journal of Applied Mathematics and Statistics, 26, 16-29.
- Shapovalov, V.I. (2005) On fundamental mechanisms of tendency control. Control Sciences, 2, 2-11.
- Klimontovich, Yu.L. (1987) Entropy evolution in selforganization processes H-theorem and S-theorem. Physica, 142A, 390-404.
- Beck, C. and Schlogl, F. (1993) Thermodynamics of chaotic systems. Cambridge University Press, Cambridge.
- Crutchfield, J.P., Farmer, J.D., Packard, N.H. and Shaw, R.S. (1986) Chaos. Scientific American, 255, 46-58.
- Berge, P., Pomeau, Y. and Vidal, Ch. (1988) L’ordre dans le chaos. Hermann, Paris.
- Denbigh, K.G. and Denbigh, J.S. (1985) Entropy in relation to incomplete knowledge. Cambridge University Press, Cambridge.
- Denbigh, K.G. (1989) Note of entropy. Disorder and disorganization. British Journal for the Philosophy of Science, 40, 323-347.
- Shapovalov, V.I. (1990) Synergetics aspect of the law of the entropy growth. In: Pleskachevskiy, U.M., Ed., NonTraditional Scientific Ideas about Nature and Its Phenomena, Club FENID, Homel., 370-372.
- Shapovalov, V.I. (2011) Entrostat. arXiv:1103.1139v1
- Shapovalov, V.I. (2005) Basis of ordering and self-organization theory. ISPO-Service, Moscow.
- Shapovalov, V.I. and Kazakov, N.V. (2008) Formation of global tendencies: Scientific hypothesis about destruction of civilizations. arXiv:0801.3030v1
- EM-DAT (2012) The OFDA/CRED international disaster database. Université Catholique de Louvain, Brussels. http://www.emdat.be/natural-disasters-trends
- Klimontovich, Yu.L. (1986) Statistical physics. Harwood Academic Publishers, New York.
- Cover, T.M. and Thomson, J.A. (1991) Elements of information theory. Wiley, New York.
- Glansdorff, P. and Prigogine, I. (1971) Thermodynamic theory of structure, stability, and fluctuations. Wiley-Interscience, New York.
NOTES
1S—the entropy of the system.
2While opening the system with the purpose of self-organizing, it is necessary to prevent the intensity of opening from exceeding a certain threshold beyond which the system would not have enough time to self-organize and would be destroyed [2].

