Natural Science
Vol.4 No.10(2012), Article ID:23913,6 pages DOI:10.4236/ns.2012.410099
Speed kills: Highly relativistic spaceflight would be fatal for passengers and instruments
![]()
1Johns Hopkins School of Medicine, Baltimore, USA; *Corresponding Author: w.edelstein@gmail.com
2University of California, San Francisco, USA
Received 11 August 2012; revised 14 September 2012; accepted 28 September 2012
Keywords: Interstellar Travel; Spaceflight; Relativistic Spaceflight; Space Travel Radiation
ABSTRACT
Highly relativistic speeds are desirable for interstellar travel. Relativistic time dilation would reduce the subjective duration of the trip for the travelers, so that they can cover galaxy-scale distances in a reasonable amount of personal time. Unfortunately, as spaceship velocities approach the speed of light, interstellar hydrogen H, although only present at a density of approximately 1.8 atoms/cm3, turns into intense radiation that would quickly kill passengers and destroy electronic instrumentation. In addition, the energy loss of ionizing radiation passing through the ship’s hull represents an increasing heat load that necessitates large expenditures of energy to cool the ship. Stopping or diverting this flux, either with material or electromagnetic shields, is a daunting problem. Going slow to avoid severe H irradiation sets an upper speed limit of v ~ 0.5 c. This velocity only gives a time dilation factor of about 15%, which would not substantially assist galaxy-scale voyages. Diffuse interstellar H atoms are the ultimate cosmic space mines and represent a formidable obstacle to interstellar travel.
1. INTRODUCTION
Stories, books and movies about space travel often describe journeys at near-light velocities [e.g. refs [1-3]]. Such high speed is desirable as the resulting relativistic time dilation reduces the subjective duration of the trip [4] so that travelers can live long enough to reach their destination. The relativistic rocket equation shows the enormous difficulty of achieving such velocities [5,6].
Interstellar H [7,8], although only present on average at a density of approximately 1.8 H atoms per cm3 [9], turns into deadly radiation [6] as spaceship velocities approach the speed of light. In addition, the energy loss of ionizing radiation passing through the ship’s hull represents an increasing heat load [5] that necessitates large expenditures of energy to cool the ship’s hull. Stopping this flux with either material or electromagnetic shields appears to be very difficult.
The effects of H-atom radiation and heating are formidable obstacles to efficient relativistic interstellar travel by people or even instrumented exploratory vessels. Yet they are not generally treated in courses or books on relativity or the physics of space travel (e.g. refs [2,10,11]).
We consider trips over distances in which cosmological expansion is not significant, e.g. within our galaxy. Then we can define a “space rest frame” which contains the trip origin and destination, and suppose that the ship is moving at velocity v relative to the space rest frame. In the space-rest frame, we assume that interstellar H atoms have small, nonrelativistic thermal velocities that we can say are approximately zero.
2. THE SHIP
For our analysis we assume a 10 m diameter spherical vessel with 0.10 m thick aluminum outer hull. This thickness is within the range of shielding that has been considered for interplanetary travel within the solar system [12]. The weight of this vessel wall would be approximately 85 metric tons (tonne).
3. RELATIVISTIC TIME DILATION/SPACE COMPRESSION
Time for the travelers is slowed by the relativistic dilation factor [4]

 (1)
(1)
where v is the spacecraft velocity and c is the speed of light. So a trip that takes time T to an external observer will have subjective duration T/ to a traveler.
to a traveler. 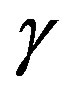 is also the factor by which space is compressed from the travelers’ viewpoint and therefore represents an increase in the density of the incident H flux.
is also the factor by which space is compressed from the travelers’ viewpoint and therefore represents an increase in the density of the incident H flux.
4. HOW FAR, HOW FAST?
Our galaxy has a diameter of about 100,000 light years. Voyager 1, now headed out of the solar system, is traveling at 17 km/s (38,000 mph). At that speed it would take about 75,000 years to go as far as the Alpha Centauri star group, our closest stellar neighbors [13,14]. Thus present rocket technology is not going to get us very far very fast in exploring the galaxy.
Our sun is approximately 25,000 light years from the galactic center [15], and it takes light 25,000 years to go that far. Suppose a traveler would like to make a trip of this distance in a reasonable personal (proper) time. Then he or she would have to travel at a velocity which gives 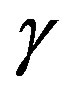 = several thousand. An efficient way to travel a distance d in reasonably comfortable fashion is to accelerate at 1g for the first d/2 (in this case, 12,500 light years) and decelerate at 1g for the second half. Using the kinematic equations for relativistic spaceflight [5] (reproduced in our Appendix for reference), the ship achieves a peak
= several thousand. An efficient way to travel a distance d in reasonably comfortable fashion is to accelerate at 1g for the first d/2 (in this case, 12,500 light years) and decelerate at 1g for the second half. Using the kinematic equations for relativistic spaceflight [5] (reproduced in our Appendix for reference), the ship achieves a peak . This trip takes 19.7 years personal time for the passengers and 25,002 years for the people back on earth.
. This trip takes 19.7 years personal time for the passengers and 25,002 years for the people back on earth.
5. H PARTICLE FLUX AND ENERGY
Interstellar atomic H was detected in 1951 from its radio signal [7,8]. Its average density is about 1.8 atoms/cm3 and varies from about 20 atoms/cm3 in diffuse clouds to 0.1 atoms/cm3 between clouds [9].
As the ship’s speed increases, so does the apparent energy of the incident H atoms, whose separated protons and electrons then penetrate the ship’s hull and irradiate the travelers and ship’s instruments.
The flux of H atoms can be calculated from the viewpoint of the ship rest frame. When it is traveling through the galaxy at velocity ≈ c, in its rest frame it is subject to a flux Φ of H atoms
 (2)
(2)
Where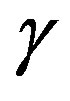 is the relativistic time dilation/space compression factor defined in Eq. 1.
is the relativistic time dilation/space compression factor defined in Eq. 1.
Thus as the ship approaches the speed of light, the energy and the flux of the incident particles both increase in a steeply nonlinear manner.
The incoming H atoms are separated into protons and electrons as soon as they encounter the hull and then become streams of separated protons and electrons.
The incident protons have rest energy mpc2 = 0.94 GEV (giga (109) electron volts), where 1 eV (electron volt) is the energy gained by a unit charged particle traversing a voltage difference of 1 volt,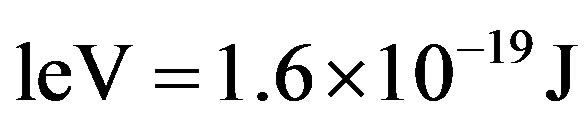 .
.
The total energy 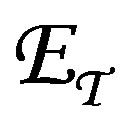 of the incident protons is therefore [4]
of the incident protons is therefore [4]
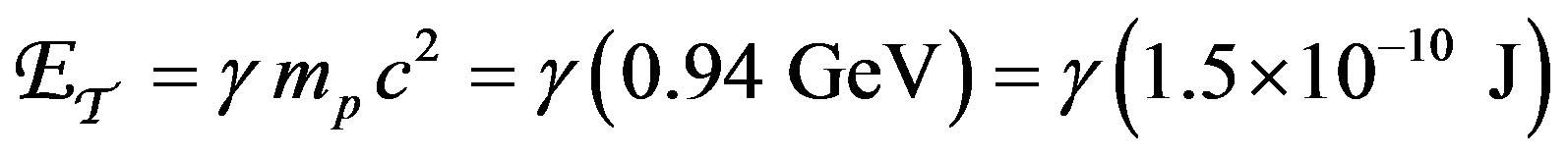 (3)
(3)
The kinetic energy  of a single proton is
of a single proton is
 (4)
(4)
The total energy and kinetic energy of the electrons in the H atoms are given by the same formulas but with the electron rest energy  (mega (106) electron volts).
(mega (106) electron volts).
Table 1 shows the kinetic energy for protons and electrons as a function of ship velocity.
6. IRRADIATION AND RADIATION DOSE
6.1. Protons
Figure 27.2 in Bichsel et al. [16] shows the energy loss for protons with energy up to about 10,000 GeV passing through various materials. For  proton kinetic energy ≥ 390 MeV, the energy loss across a range of materials is approximately
proton kinetic energy ≥ 390 MeV, the energy loss across a range of materials is approximately
 (5)
(5)
Note that it is necessary to multiply Eq. 5 by material density (kg/m3) to get energy loss (energy deposition) per unit distance for various materials.
Protons at the high energies listed in Table 1 will pass through the Al hull with very small energy loss (more on this below) and would irradiate travelers and equipment inside the ship. For the purposes of this calculation, we will use the Eq. 5 approximate figure for the energy loss 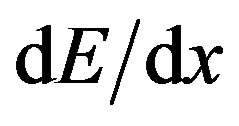 in people (mostly water) or electronics (e.g. Si).
in people (mostly water) or electronics (e.g. Si).
The irradiation energy deposited per unit volume is given in units of grays (J/kg, abbrev Gy). The dose in sieverts (Sv) to people is the energy deposition multiplied by a radiation weighting factor [17]. The weighting factor for protons [17] is 2, so the conversion from power to dose rate for body tissues is
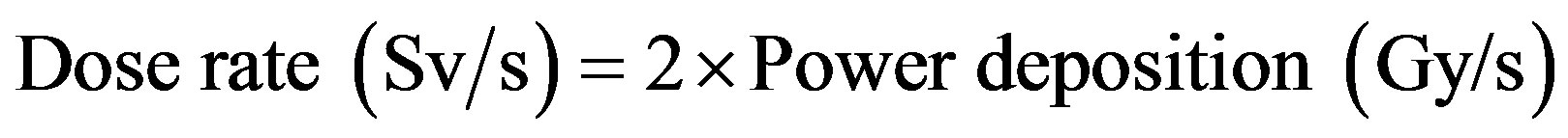 (6)
(6)
For the crew and equipment inside the ship, which is traveling close to the speed of light, the total energy deposited per unit time is given by
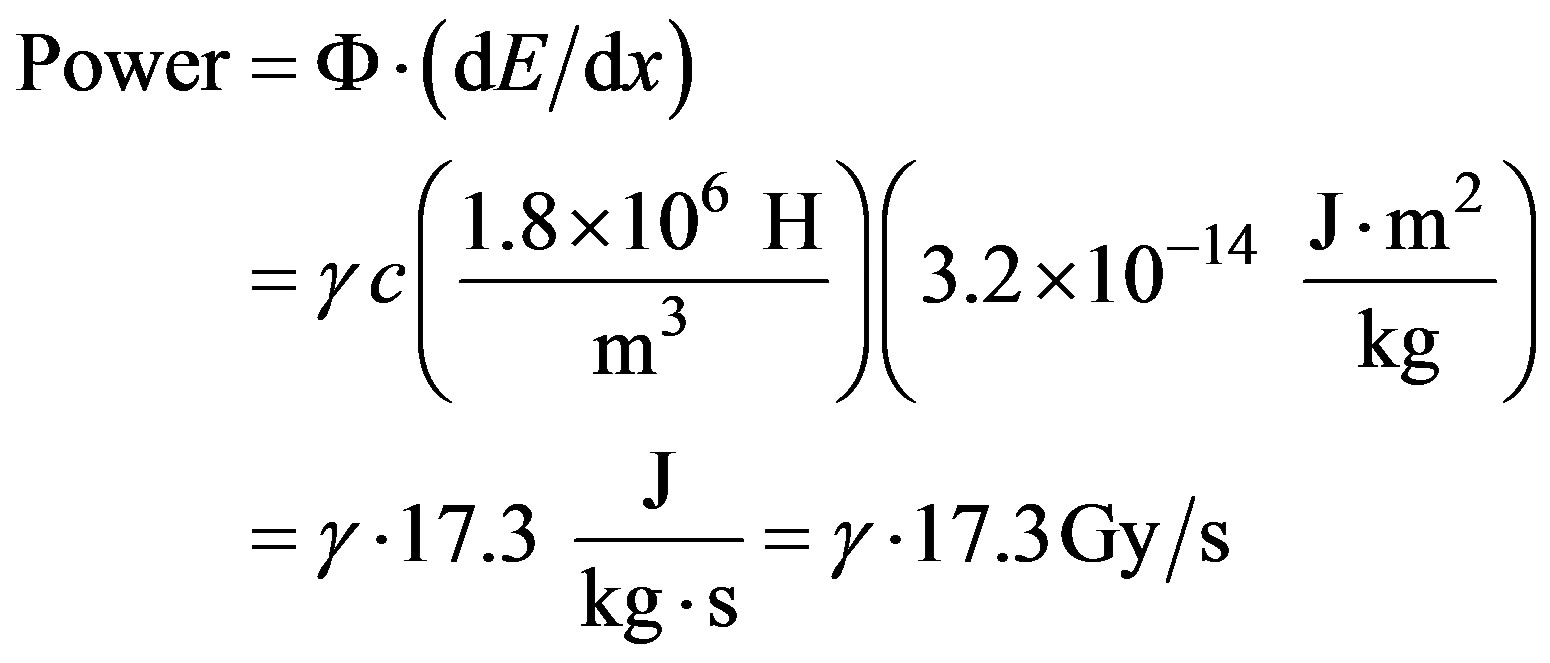 (7)
(7)

Table 1. Total kinetic energy of approaching protons and electrons for some relativistic spaceship velocities.
So the dose rate for the crew and electronics is
 (8)
(8)
Table 2 shows the dose rate for various relativistic velocities.
An acute dose of over 6 Sv is generally fatal ([18], p. 421), so it is readily apparent that relativistic travel under these conditions is not possible for human passengers.
It is interesting to compare the Large Hadron Collider (LHC) beam current with the atomic H flux in our example [6]. The LHC beam [19] consists of 2808 particle bunches with 1011 particles per bunch, and the beam circulates in 89 ms, which is a total proton flux ~3.2 × 1018 – s–1. The relativistic atomic H flux in our example for 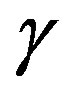 = 7000 is 3.8 × 1018 – s–1·m–2. Thus spreading the LHC proton beam over 1 m2 would give approximately the same areal flux as that experienced by the relativistic spaceship.
= 7000 is 3.8 × 1018 – s–1·m–2. Thus spreading the LHC proton beam over 1 m2 would give approximately the same areal flux as that experienced by the relativistic spaceship.
Ionizing radiation can also damage electronic circuits. “Radiation hardened” CMOS circuits have ratings of 1 - 3 kGy [20]. So electronics would not survive long either.
6.2. Electrons
The behavior of high-energy electrons is complex and we will not attempt to calculate their effects here. At very high energies, impinging electrons will produce electronphoton cascade showers, ([18], p. 145) and these will pose a high level of dangerous radiation to passengers. We note that 1000 MeV electrons ( = 2000) have a range of about 101 g/cm2 which is about 37 cm in Al. So electrons of this or greater energy would easily penetrate our ship with a 10 cm Al hull, and in so doing would generate intense electron and photon radiation incident on the interior.
= 2000) have a range of about 101 g/cm2 which is about 37 cm in Al. So electrons of this or greater energy would easily penetrate our ship with a 10 cm Al hull, and in so doing would generate intense electron and photon radiation incident on the interior.
7. FRICTION, HEATING AND DRAG FORCE
The passage of protons through the ship’s hull will heat the ship and will also cause drag.
Heat = energy  deposited in the ship’s hull per unit time:
deposited in the ship’s hull per unit time:

Table 2. Interstellar H proton radiation dose for travelers and electronics at relativistic velocities.
 (9)
(9)
where dE/dx is given by Eq. 5,  by Eq. 2 and
by Eq. 2 and  is 85 tonne, the total mass of the ship’s hull.
is 85 tonne, the total mass of the ship’s hull.
The drag force 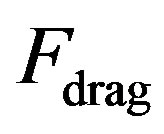 exerted on the ship is given by the change in momentum per unit time applied by the slowing H atoms i.e.
exerted on the ship is given by the change in momentum per unit time applied by the slowing H atoms i.e.
 (10)
(10)
since for highly relativistic particles,
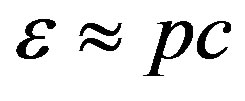 (11)
(11)
We have also calculated  (time to heat the Al hull from 0 K to 932 K, Al melting temperature), assuming only radiative heat loss, from the following integral.
(time to heat the Al hull from 0 K to 932 K, Al melting temperature), assuming only radiative heat loss, from the following integral.
 (12)
(12)
where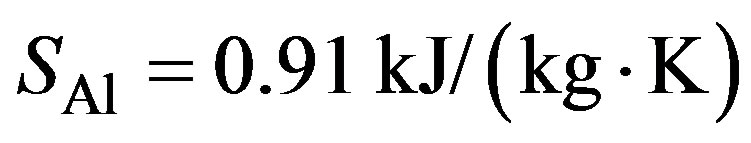
 = specific heat of Al,
= specific heat of Al,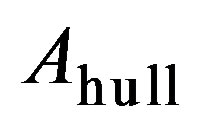 is the surface area of the ship’s hull,
is the surface area of the ship’s hull, 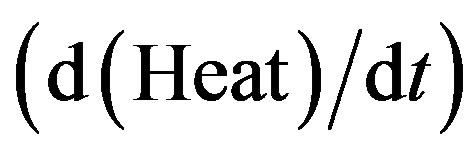 is the heat deposited shown in Table 3,
is the heat deposited shown in Table 3,  = Stefan’s constant and T is the temperature in K. We note that the radiative loss for this vessel would be only about 13.5 MW at 932 K. This is far less than the heat deposited for all but the lowest
= Stefan’s constant and T is the temperature in K. We note that the radiative loss for this vessel would be only about 13.5 MW at 932 K. This is far less than the heat deposited for all but the lowest in Table 3.
in Table 3.
As mentioned above, the proton flux would destroy biological activity in the travelers’ bodies in a fraction of a second. In addition, heat deposited in a living passenger would boil the water comprising body tissue. For with a deposition of
with a deposition of 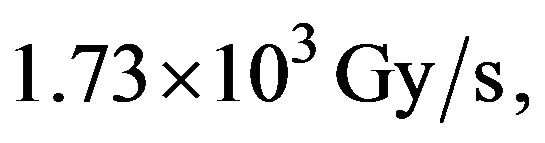 it would take approximately 1.5 s to raise body water temperature from 37˚C to 100˚C.
it would take approximately 1.5 s to raise body water temperature from 37˚C to 100˚C.
We have also calculated the drag force, shown in the last column of Table 3. This is small, but it indicates the need for continuous thrust, even if the ship is “coasting.”
8. A SOLID SHIELD?
Material shielding would have to be massive because
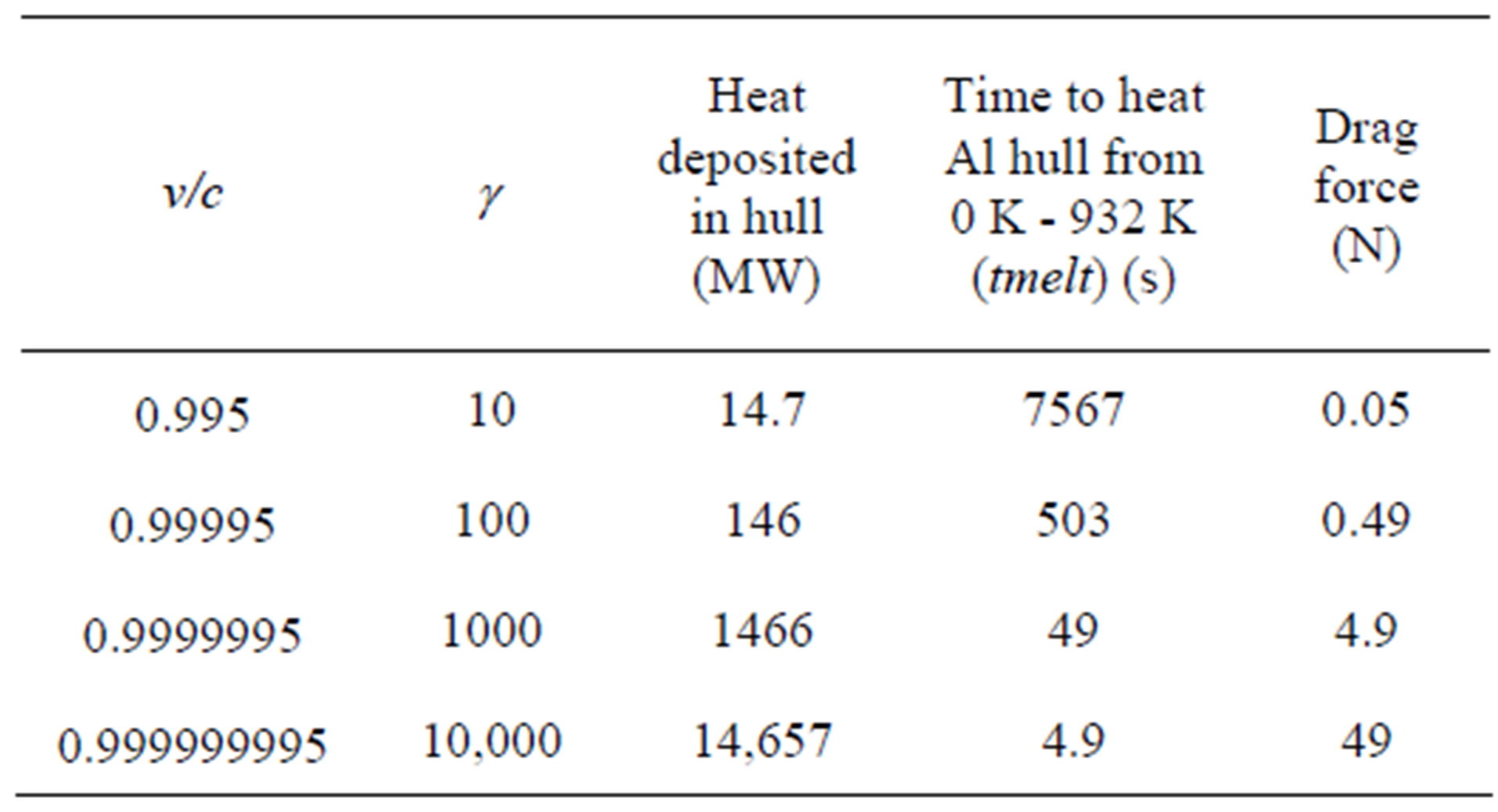
Table 3. Heating and drag force on ship’s hull (10 m diameter, 0.074 m thick Al) produced by proton flux.
the incident protons have such enormous penetrating power. A large shielding mass would then be problematic because of the huge increases in fuel requirements per the relativistic rocket equation [5].
We can calculate the range of high energy protons assuming
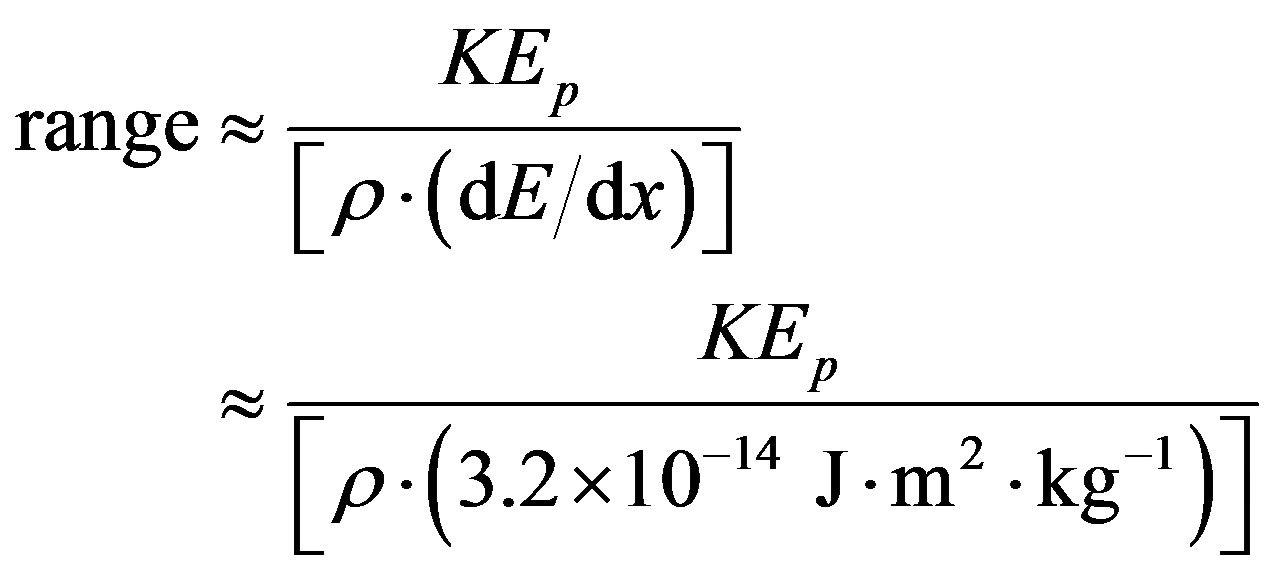 (13)
(13)
where we have used the 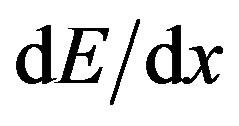 in Eq. 5.
in Eq. 5.
A solid shield with the ship diameter (10 m) built and placed in front of the ship would have a mass independent of the material since range in Eq. 13 is inversely proportional to density. The mass of such a shield—shown in the third column of Table 4—is enormously greater than the original 85 tonne mass of our assumed 10 cm thick Al hull. The range of protons in Al, Fe and Pb are approximately 18.5 m, 6.4 m and 4.4 m, respectively, for the lowest value of proton kinetic energy 10 Gev (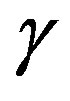 =10). Multiple thicknesses of these materials would be needed to achieve significant shielding. The resulting mass would hugely increase the fuel or laser push required to drive the ship.
=10). Multiple thicknesses of these materials would be needed to achieve significant shielding. The resulting mass would hugely increase the fuel or laser push required to drive the ship.
9. ELECTROSTATIC OR MAGNETIC SHIELDING
There is substantial literature regarding shielding for spaceflight within the solar system [21]. This includes the possibility of using electric and magnetic fields to deflect incoming charged particles.
H atoms must be separated into protons and electrons before they can be affected by electric or magnetic fields. The H could be ionized by positioning a thin sheet shield ahead of the ship to intercept the incoming H atom flux. The separated protons and electrons would then proceed forward as charged particles.
In order to stop the protons with an electric field, it would be necessary to charge the ship’s hull to billions (or trillions) of volts, i.e., to a voltage which equals the incoming proton kinetic energy. Of course that would attract electrons. The hull would eventually tear itself apart.
Let us consider the possibility of deflecting incoming particles with a magnetic field B. For particles with charge q traveling close to the speed of light, the relationship between magnetic force F and resulting circular deflection is
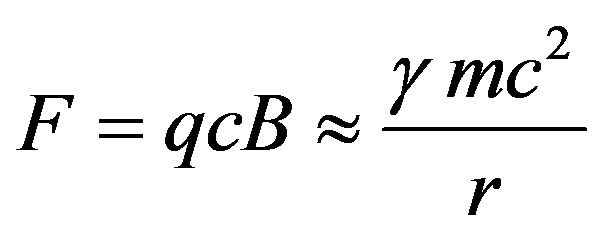 (14)
(14)
resulting in a particle circular path of radius r. We can solve for r and Table 4 shows some results assuming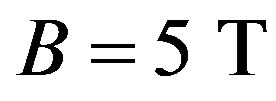 , a field that has been achieved for whole-body MRI.
, a field that has been achieved for whole-body MRI.
To be effective, it would be necessary to extend the deflecting magnetic field well beyond the ship to at least a distance of the radius of curvature r. This would be several meters for the smallest and over 6 km for 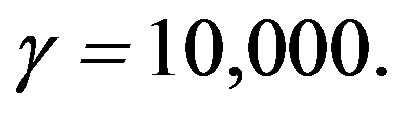 Note that 6 km is not too different from the LHC proton beam curvature (radius 4.3 km). Protons in the LHC have
Note that 6 km is not too different from the LHC proton beam curvature (radius 4.3 km). Protons in the LHC have = 7440 and the LHC ring has 1232 separate bending magnets [19].
= 7440 and the LHC ring has 1232 separate bending magnets [19].
There are a myriad of problems with such a shielding scheme for our space vessel. At present, nobody knows how to make the required large volume, high B field. Large magnets have large masses. Some particles at the edges of the field might be deflected into the ship, causing irradiation that the magnetic field was created to avoid. The magnetic field must also be designed so there is little or no field inside the spacecraft, since significant fields could exert forces on ferromagnetic objects, create eddy currents in moving conducting objects and inhibit their motion, interfere with electronics, and produce unpleasant sensory effects in passengers [22]. Shielding by magnetic deflection seems difficult, to say the least, for relativistic spacecraft.
10. SPEED LIMIT?
The extreme radiation doses listed in the last column of Table 2 raise the question of whether there is a maximum speed at which humans or instruments could travel and survive the H flux irradiation.
One upper limit might be the speed at which the 10 cm thick Al hull acts as an effective shield. We can roughly estimate this speed by looking at the range for protons in Al [23]. The projected range is 10 cm at a proton kinetic energy of 177 MeV and 5 cm at 118 MeV, the latter figure giving a safety factor of 2× in thickness. These data points correspond, respectively, to v/c values of 0.54 and 0.46.
Let us then consider a rough upper speed limit of  Unfortunately, this results in
Unfortunately, this results in 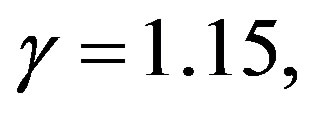 i.e.
i.e.
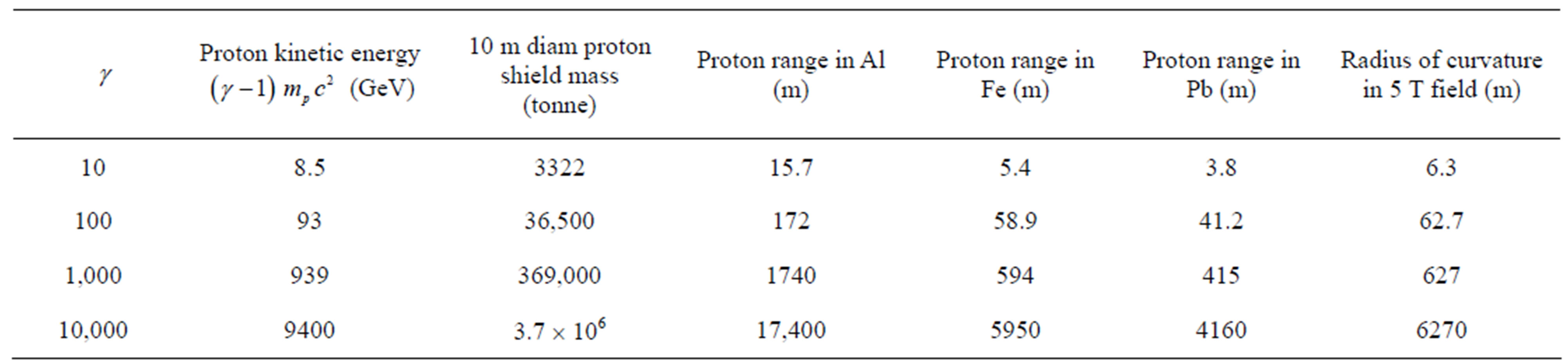
Table 4. Shielding: solid shield mass; proton range in Al, Fe and Pb; curvature radius for protons in 5 T magnetic field.
only a 15% reduction in personal time for a human passenger, which is not helpful for traveling significant distances across the galaxy by rocket.
We can calculate the H power dissipated at v = 0.5c. By our shielding assumption, all incident H kinetic energy will be deposited in the ship. Using Eq. 2 to calculate flux, Eq. 4 to get the kinetic energy, and the cross-sectional area of the ship  we obtain
we obtain
 (15)
(15)
which represents a considerable heat load.
Our “speed limit” estimate is obviously crude, and a detailed examination of shielding for relativistic or near relativistic travel is beyond our scope here. We note that the annual dose limit for a radiation worker is 0.05 Sv (NRC, 2011), so shielding must be extremely effective to keep dose down to this level. Instrumentation must be similarly very well shielded, since even small doses over long times can exceed the cumulative dose limits for electronics of 1 - 3 kGy [20,24] .
11. DISCUSSION AND CONCLUSIONS
There are many obstacles to sending people or probes across the enormous distances of interstellar space. It is clearly desirable to take advantage of relativistic time dilation/space compression by traveling very close to the speed of light. One big problem for a rocket is the requirement for huge amounts of fuel-thousands, millions (or more) times the mass of the ship-depending on the final [5,6].
[5,6].
The present paper details a further issue with relativistic travel, namely intense irradiation of any spacefaring vessel plowing through the dispersed H atoms in space [6], which might be called the ultimate cosmic space mines. Of course, hitting any macroscopic piece of matter would also be a disaster. A speed limit based on shielding limited to avoid H atom irradiation limits velocity to less than about 0.5 c, which does not give a useful relativistic time dilation factor. Pushing a ship to highly relativistic velocities using a light sail [1,3] would not avoid deadly H irradiation.
12. APPENDIX-RELATIVISTIC KINEMATIC EQUATIONS
For reference purposes, we list below the relativistic rocket kinematic equations [5].
c = speed of light, a = acceleration, v = velocity, d = distance traveled, T = proper time of traveler, and t = time elapsed according to home observers.
Then
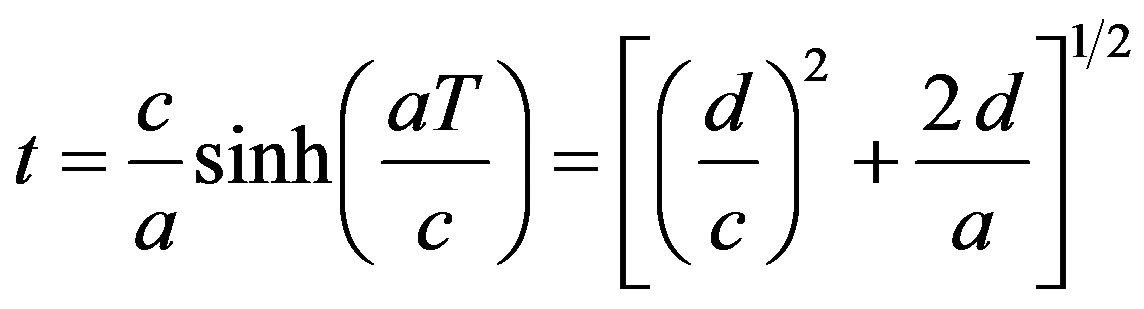 (A1)
(A1)
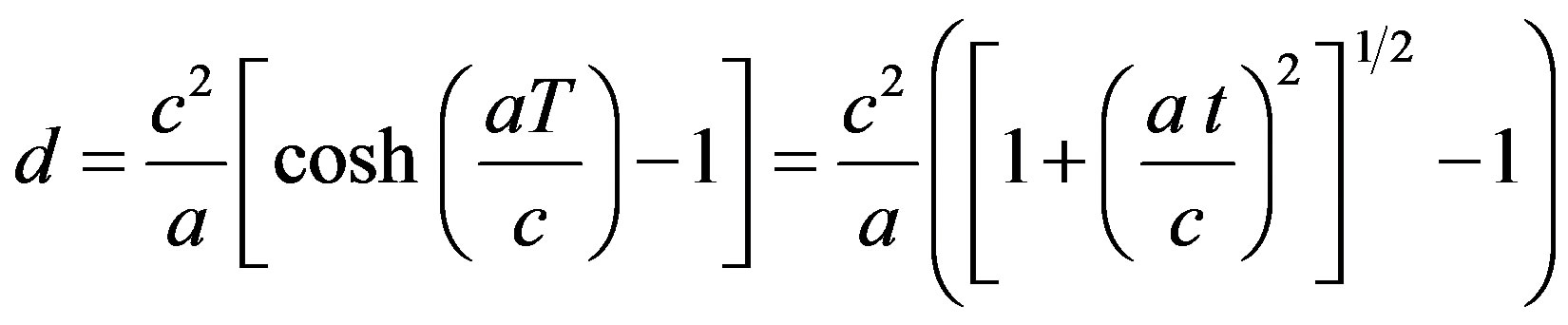 (A2)
(A2)
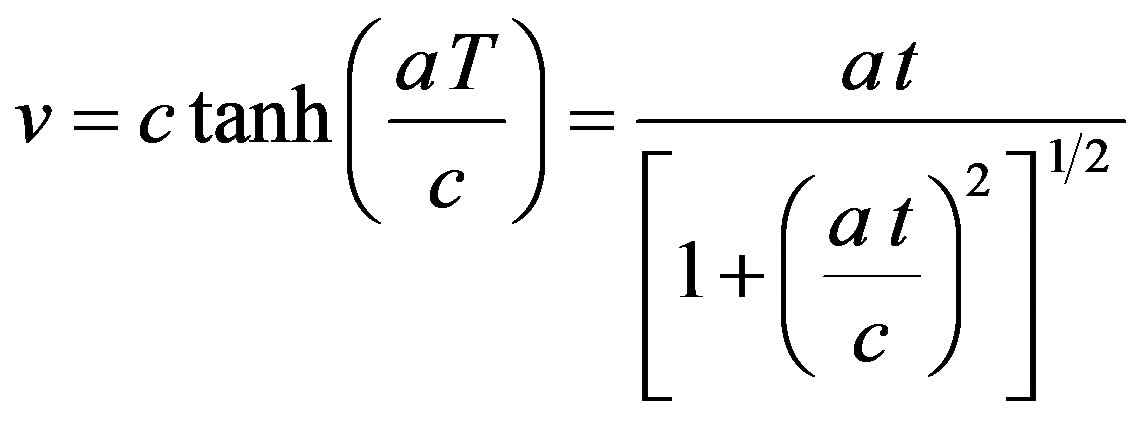 (A3)
(A3)
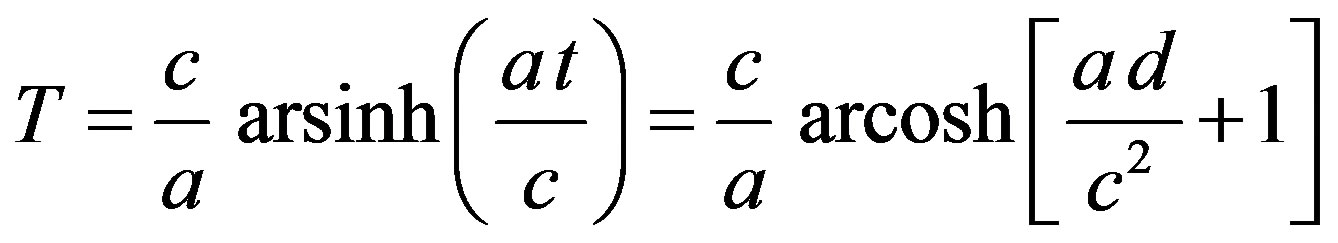 (A4)
(A4)
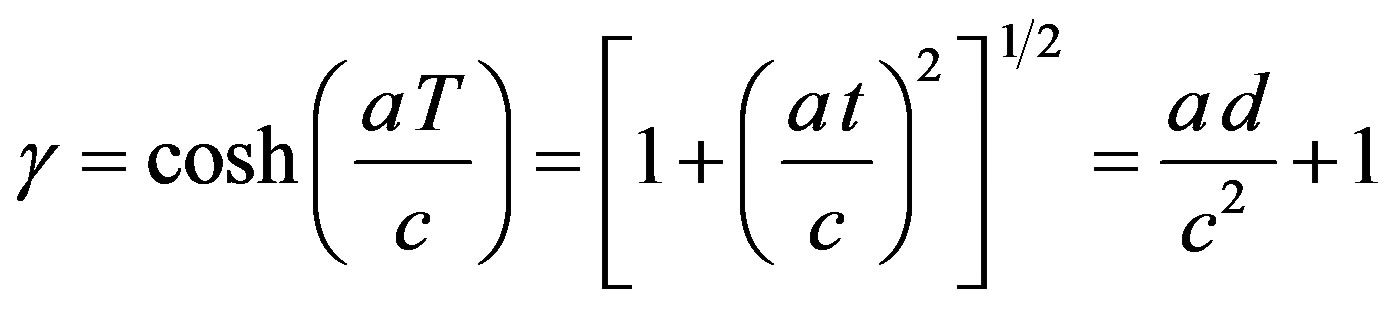 (A5)
(A5)
REFERENCES
- Forward, R.L. (1984) Roundtrip interstellar travel using laser-pushed lightsails. Journal of Spacecraft, 21, 187- 195. doi:10.2514/3.8632
- Krauss, L.M. (1995) The physics of star trek. Harper Perennial, New York.
- Forward, R.L. (1984) Flight of the dragonfly. Simon and Schuster, New York.
- French, A.P. (1968) Special Relativity. CRC Press, Boca Raton.
- Gibbs, P. and Koks, D. (2006) The relativistic rocket. http://math.ucr.edu/home/baez/physics/Relativity/SR/rocket.html
- Purcell, E.M. (1963) Radioastronomy and communication through space. In: Cameron, A.G.W., Ed., Interstellar Communication, W. A. Benjamin, Inc., New York.
- Ewen, H.I. and Purcell, E.M. (1951) Observation of a line in the galactic radio spectrum. Nature, 168, 356. doi:10.1038/168356a0
- Muller, C.A. and Oort, J.H. (1951) The interstellar hydrogen line at 1420 Mc./sec., and an estimate of galactic rotation. Nature, 168, 357-358. doi:10.1038/168357a0
- Frederick, L.W. (1989) Astronomy and astrophysics. In Anderson, H.L., Ed., A Physicists Desk Reference, American Institute of Physics, New York, 66-78.
- Resnick, R. and Halliday, D. (1992) Basic Concepts in Relativity. Maxwell Macmillan International, New York.
- Mermin, N.D. (2005) It’s about time. Princeton University Press, Princeton.
- Hellweg, C.E. and Baumstark-Khan, C. (2007) Getting ready for the manned mission to Mars: The astronauts’ risk from space radiation. Naturwissenschaften, 94, 517- 526. doi:10.1007/s00114-006-0204-0
- “Alpha Centauri,” Wikipedia. http://en.wikipedia.org/wiki/Alpha_Centauri#cite_note-S-9
- Gilster, P. (2011) What are the fastest spacecraft we’ve ever built? http://io9.com/5786083/what-are-the-fastest-spacecrafts-ever-built
- Milky Way, Wikipedia. http://en.wikipedia.org/wiki/Milky_Way#cite_note-ask-astro-0
- Bichsel, H., Groom, D.E. and Klein, S.R. (2010) Passage of particles through matter. http://pdg.ge.infn.it/reviews/rppref/sports/2010/passage-rpp.pdf
- Wrixon, A.D. (2008) New ICRP recommendations. Journal of Radiological Protection, 28, 161-168. doi:10.1088/0952-4746/28/2/R02
- Turner, J.E. (2007) Atoms, radiation and radiation protection. 3rd Edition, Wiley-VCH, Berlin.
- Lefevre, C. (2009) CERN Faq: LHC, the guide. http://tinyurl.com/yfcowz5
- Dodd, P.E., et al. (2010) Current and future challenges in radiation effects on CMOS electronics. IEEE Transactions on Nuclear Science, 57, 1747-1763. doi:10.1109/TNS.2010.2042613
- Townsend, L.W. (2005) Critical analysis of active shielding methods for space radiation protection. 2005 IEEE Aerospace Conference, Montana, 5-12 March 2005, 724- 730.
- Schenck, J.F. (2005) Physical interactions of static magnetic fields with living tissues. Progress in Biophysics & Molecular Biology, 87, 185-204. doi:10.1016/j.pbiomolbio.2004.08.009
- Burger, M.J., et al. (1993) Stopping powers and ranges for protons and alpha particles. ICRU Report, Report NO. 49.
- pstar: Stopping-Power and Range Tables for Protons. http://physics.nist.gov/PhysRefData/Star/Text/PSTAR.html

