Natural Science
Vol.4 No.12A(2012), Article ID:26115,12 pages DOI:10.4236/ns.2012.412A137
Influence β-radioactive radiation on tissues of the organism
![]()
Samara State Medical University, Samara, Russia; *Corresponding Author: volobuev@samaramail.ru
Received 6 July 2012; revised 10 August 2012; accepted 24 August 2012
Keywords: β-Rays; Brake Electromagnetic Radiation; Parameter of Efficiency of Braking of Electrons; Linear Energy Transfer
ABSTRACT
Research of interaction of β-radioactive radiation with biotissue of an organism is lead. It is shown, that during electrons moderation there is a brake electromagnetic radiation usually in an X-ray range. There are derivatives of the formulas in not relativistic and relativistic variant for a finding of dependence of a flux brake electromagnetic radiation from frequency, of charging number elements of a biotissue, of a parameter of efficiency braking of electrons, of initial intensity of a flux of electrons and initial energy of electrons, is given.
1. INTRODUCTION
Influence ionizing radiations on an organism is carried out due to the various physical phenomena. For example, at influence X-ray and g-radiations on a biotissues: Processes of coherent and not coherent scattering, an internal photo effect, formation of an electron-positron pair, etc. are observed. Influence α-, β-, proton, neutron, etc. radioactive radiations also are accompanied by the various phenomena. All these phenomena are desirable for taking into account at prescribe of procedures of radiation therapy.
For example we shall consider some physical processes of interaction of a flux of β-particles, i.e. electrons with tissues of an organism. β-rays are used in a number of oncological diseases, in particular malignant lymphoma [1].
The following phenomena are possible at interaction of β-particles with biotissues [2]:
• Elastic collisions of electrons with atoms at which energy of electrons practically does not vary;
• Non elastic collisions of electrons with atoms at which energy of electrons is lost on excitation and ionization of atoms;
• Non elastic collisions of electrons with nucleus and electrons of the atoms, accompanying with formation of brake radiation.
In Table 1 the ratio of losses of energy of the electrons moving in biotissues going on brake radiation, to the losses of energy going on excitation and ionization of atoms is shown, depending on energy of electrons falling on a biotissue [2].
Apparently from Table 1 of loss on brake radiation are compared with so-called “ionizing losses” at energy of electrons close to 1 MeV.
Energy of electrons of β-rays depends on radioactive element which radiates these rays. For a spectrum β-rays it is typically existence of the top power border. For example, isotope 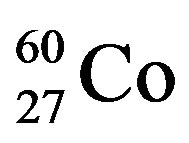 widely used in medicine has two spectra β-rays. The top border of a low-energy spectrum of electrons is E0 = 318 keV, and high-energy spectrum E0 = 1491 keV [3]. The basic fraction of β-rays 99.9% falls at a low-energy spectrum. Short-wave boundary length of a wave of brake radiation (if all energy of the electron is transferred to a photon) for a low-energy spectrum is
widely used in medicine has two spectra β-rays. The top border of a low-energy spectrum of electrons is E0 = 318 keV, and high-energy spectrum E0 = 1491 keV [3]. The basic fraction of β-rays 99.9% falls at a low-energy spectrum. Short-wave boundary length of a wave of brake radiation (if all energy of the electron is transferred to a photon) for a low-energy spectrum is
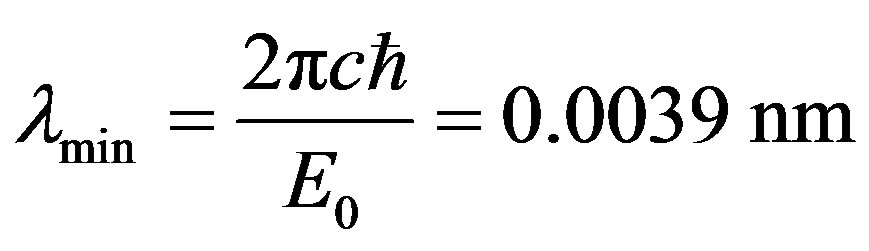 , for a high-energy spectrum is
, for a high-energy spectrum is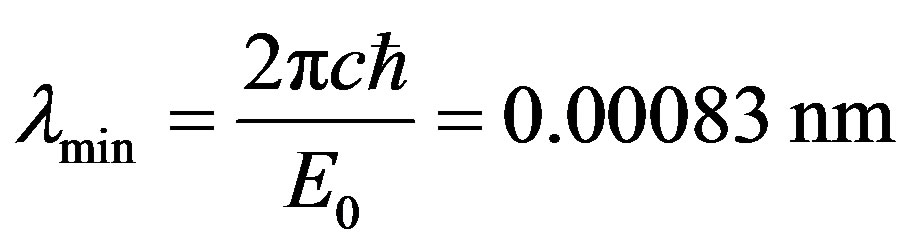 , where c is a speed of light in vacuum,
, where c is a speed of light in vacuum, 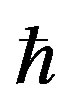 -reduced Planck’s constant. The average lengths of waves counted on average energy of electrons, are correspondingly
-reduced Planck’s constant. The average lengths of waves counted on average energy of electrons, are correspondingly  = 0.0012 nm and
= 0.0012 nm and  = 0.00032 nm. All these lengths of a wave lay in the region of short-wave X-ray. We shall note, that top power border of electrons of β-rays for used in medicine radioactive elements seldom exceeds 2 MeV [3].
= 0.00032 nm. All these lengths of a wave lay in the region of short-wave X-ray. We shall note, that top power border of electrons of β-rays for used in medicine radioactive elements seldom exceeds 2 MeV [3].
Electrons of β-rays will rather deeply penetrate into biotissues of an organism. For example, electrons with energy 150 keV will penetrate on depth of 0.278 mm, and with energy 50 MeV on depth of 19 sm [4]. For electrons linear energy transfer (LET) sharply falls with increase of their energy and makes 0.21 keV/μm for energy above 450 keV [4].
At prescribe of the medical-diagnostic procedures
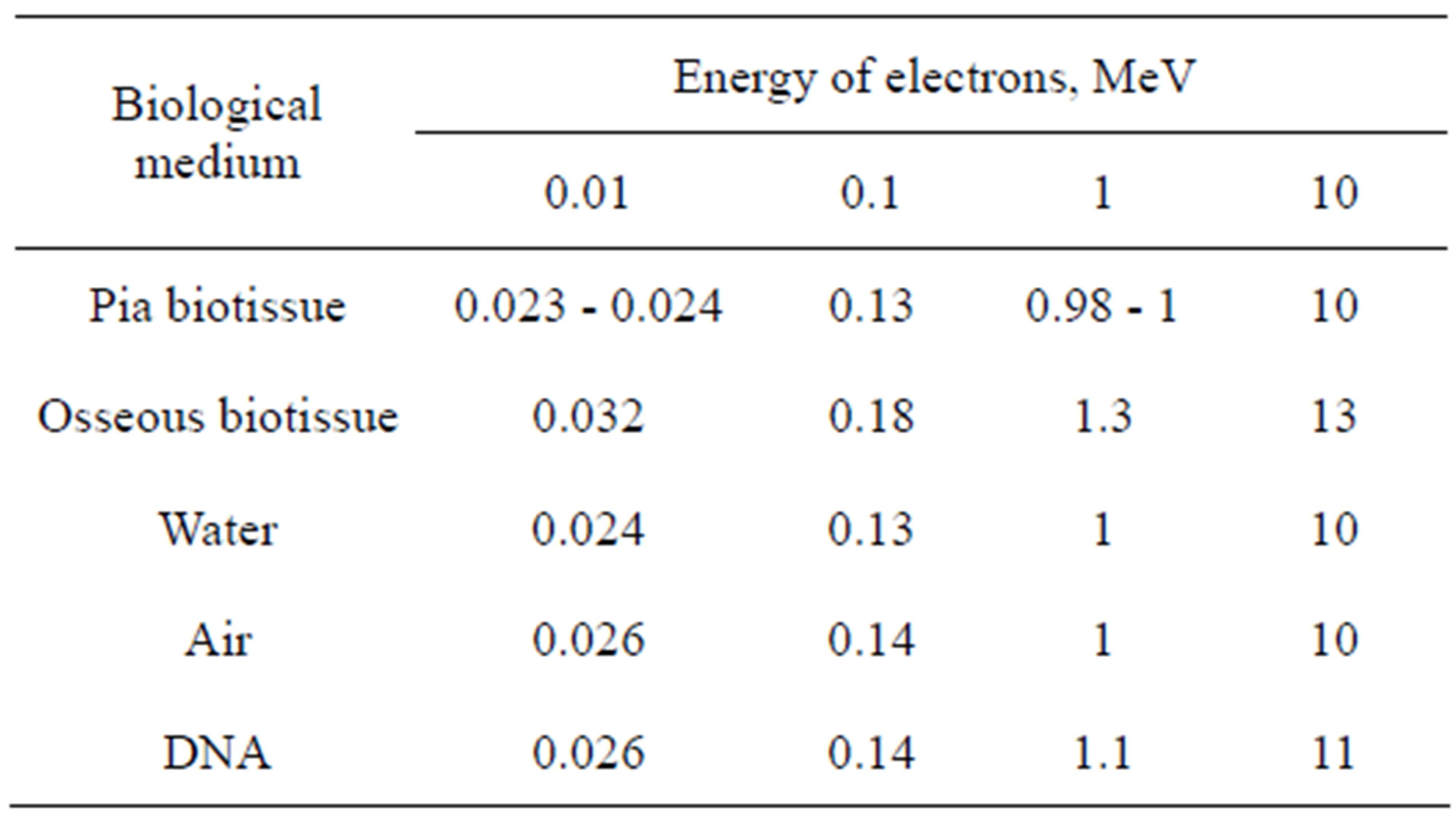
Table 1. The ratio of losses of energy of moving electrons in substance going on brake radiation to energy going on ionization and excitation of atoms.
connected to an irradiation of biotissues by β-particles, it is necessary to take into account, that at braking electrons of big energy there is a X-ray radiation which has killing action on cells of an organism. This phenomenon should be taken into account at calculation of spatial distribution of the absorbed doze of β-radiation which is proportional to LET [4], and also for more exact estimation of biological effects of influence of radiation on various parts of an organism.
The interesting experimental fact is the identical radiating effect on a biotissues ionizing electromagnetic radiations and β-rays [4]. For an explanation of the given phenomenon it is necessary to consider in more detail movement of the electron of β-radiation in a biotissue.
2. THE ANALYSIS OF OCCURRENCE OF BRAKE RADIATION AT MOVEMENT OF THE ELECTRON IN A BIOTISSUE. NON RELATIVISTIC VARIANT
Let’s consider in more detail braking with scattering of the electron moving in a field of a nucleus (Figure 1).
During flight of the electron about a nucleus there is dipole configuration of charges. The dipole moment is directed usually from the electron to a nucleus. For convenience we shall assume, that it is directed against a unit vector n which is directed on a radius-vector of the electron.
During movement of the electron the dipole moment rotates in a plane of scattering of the electron. The maximal probability of a start of quantums of brake radiation has in a direction of perpendicular axes of a dipole. This probability is distributed in spherical coordinates under the sine wave law. The diagram of radiation of quantums is shown on Figure 1.
Assuming, that at interaction of one moving electron with an electric field of a nucleus one photon radiated, we shall write down the operator (Hamiltonian) radiations of a photon with an impulse k, system an electronnucleus [5]:
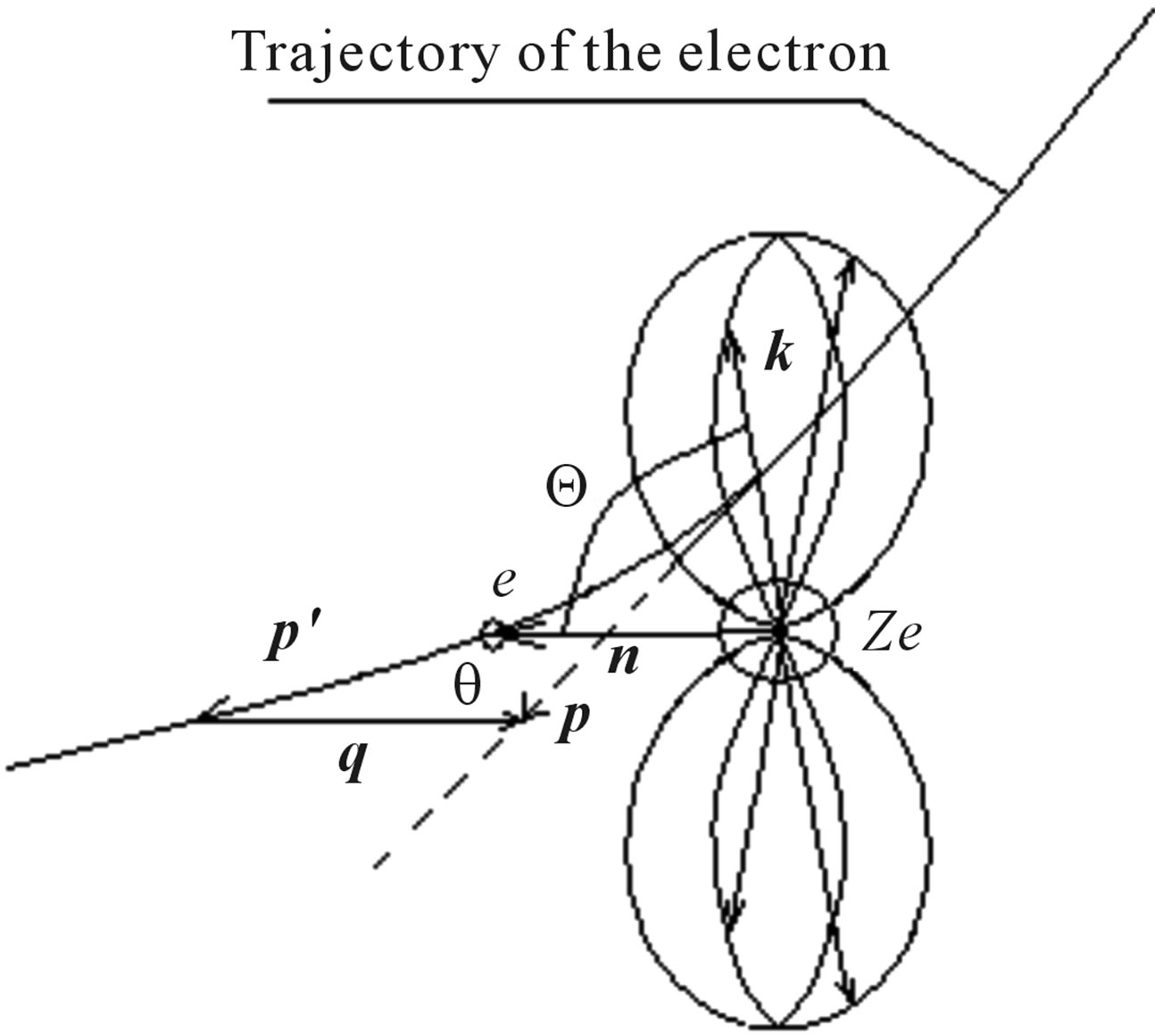
Figure 1. The scheme of occurrence of electromagnetic radiation at braking β-electrons.
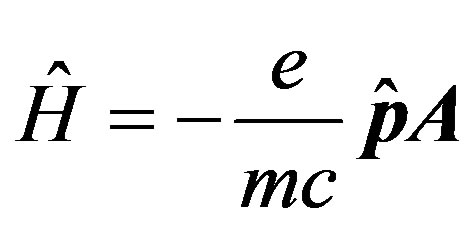 , (1)
, (1)
where е is a charge of the electron, m—its mass, Z—charging number of a nucleus, r—a radius-vector up to a considered point of space in a direction of radiation of a photon,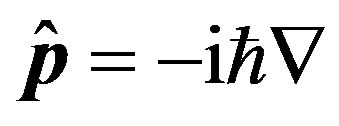 —the operator of an impulse of the electron [6],
—the operator of an impulse of the electron [6], —the vectorpotential of a photon is radiating periodic function of coordinates (the radius r is directed on an impulse of a photon k, that is why used scalar forms of radius and a pulse), w—cyclic frequency of a photon, e—a unit vector of polarization of a photon which is always perpendicular to a vector of an impulse of a photon k, V—some normalizing volume,
—the vectorpotential of a photon is radiating periodic function of coordinates (the radius r is directed on an impulse of a photon k, that is why used scalar forms of radius and a pulse), w—cyclic frequency of a photon, e—a unit vector of polarization of a photon which is always perpendicular to a vector of an impulse of a photon k, V—some normalizing volume,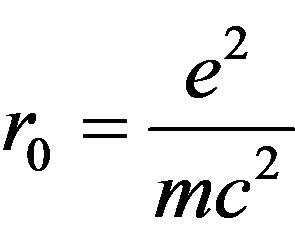 —classical radius of the electron [7]. It is taken into account, that the formula for vector-potential should not include mass of the electron, but in it there should be a value of potential energy of a field
—classical radius of the electron [7]. It is taken into account, that the formula for vector-potential should not include mass of the electron, but in it there should be a value of potential energy of a field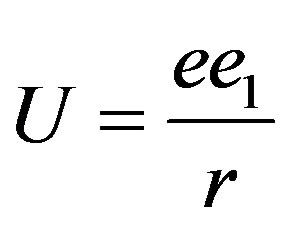 , where
, where 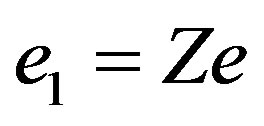 is a charge of a nucleus about which the photon is propagated. The factor in the formula for vector-potential,
is a charge of a nucleus about which the photon is propagated. The factor in the formula for vector-potential, 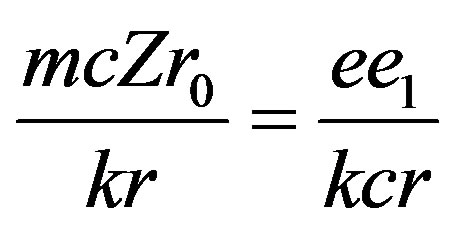 is the ratio of potential energy of a field to energy of the radiated photon. All transformations as it is accepted in quantum mechanics, we carry out in system C.G.S.
is the ratio of potential energy of a field to energy of the radiated photon. All transformations as it is accepted in quantum mechanics, we carry out in system C.G.S.
Let’s find a matrix element of energy of interaction of the electron moving in a field of a nucleus, at change of an impulse of the electron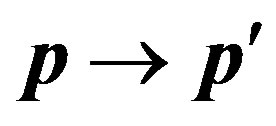 , where р is an initial impulse of the electron, and
, where р is an initial impulse of the electron, and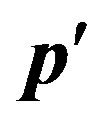 —its impulse after scattering on a nucleus. We assume a nucleus is the heavy motionless center. In this case change of an impulse of the electron
—its impulse after scattering on a nucleus. We assume a nucleus is the heavy motionless center. In this case change of an impulse of the electron 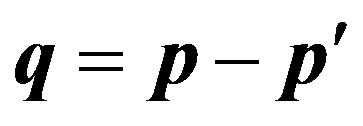 on the module is equal to an impulse of the radiated photon
on the module is equal to an impulse of the radiated photon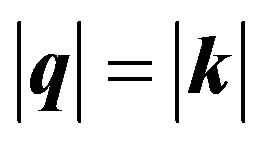 .
.
In vector-potential A it is necessary to transit from a radius-vector in a direction of radiation of a photon to a radius-vector in a direction of the electron since further wave functions of the electron with its radius-vector will be used. Taking into account a angle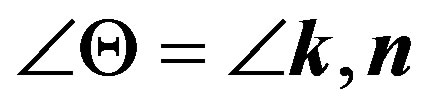 , Figure 1, we shall write down:
, Figure 1, we shall write down:

Simultaneously we used replacement . A unit vector in a direction of the electron is
. A unit vector in a direction of the electron is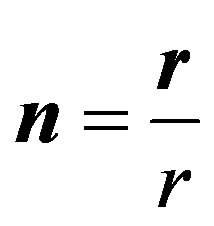 . In this case scalar product in exponent conditionally means
. In this case scalar product in exponent conditionally means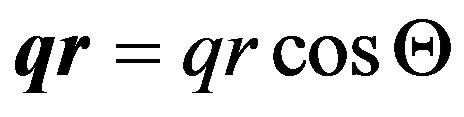 , in spite of the fact that between vectors q and r the angle is equal to 180°, Figure 1.
, in spite of the fact that between vectors q and r the angle is equal to 180°, Figure 1.
In spite of the fact that transformations will be written at once concerning a radius-vector of the electron, actual transition for convenience will be made later about what we shall tell below.
The matrix element of energy of radiation of a photon at interaction of the electron and a field of a nucleus can be written down as (in this case r—a radius-vector of the electron):
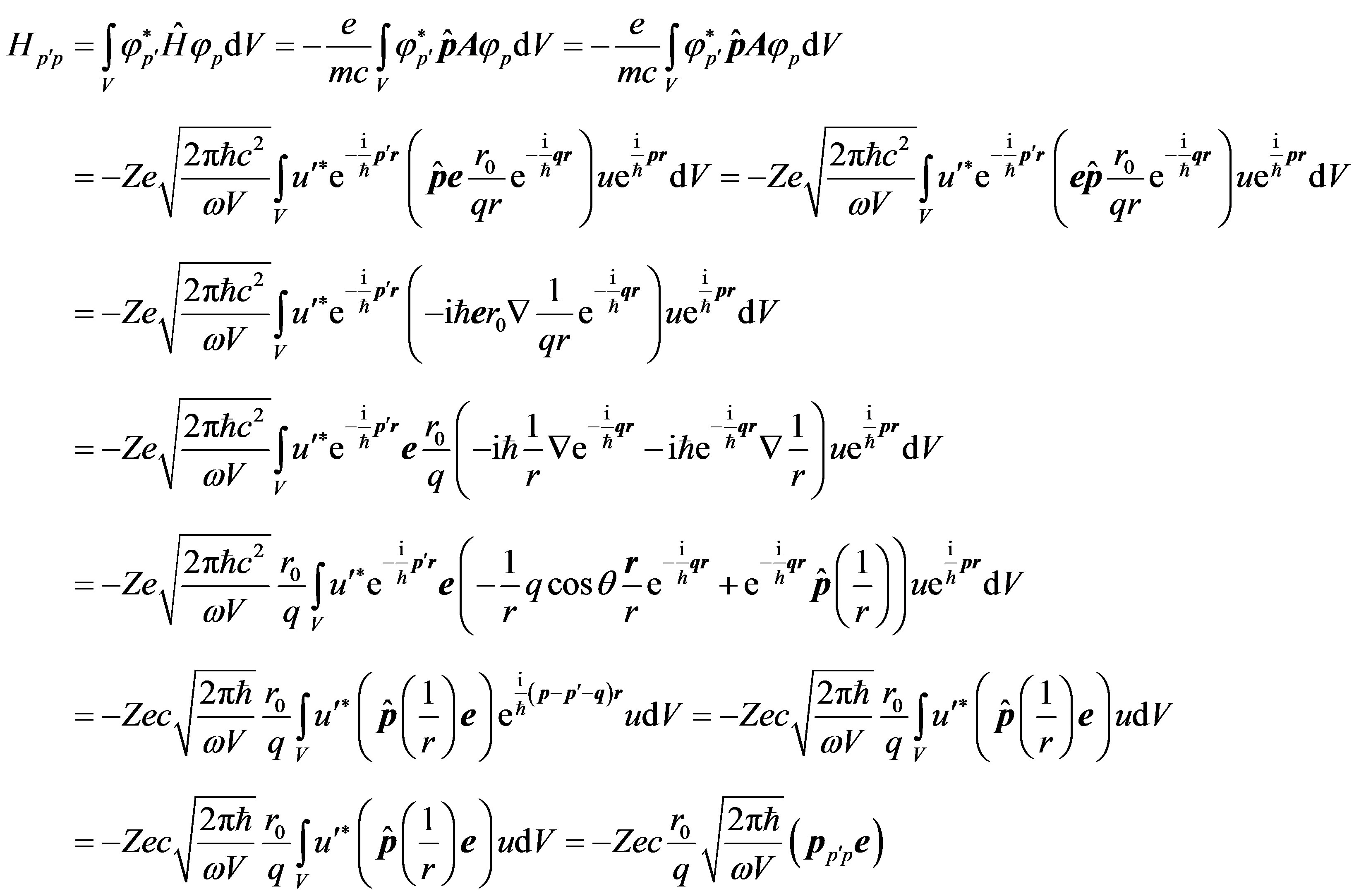 (2)
(2)
where taken into account the condition  since in (2) transition to a radius-vector of the electron is carried out really only before collecting of exponents. It is used
since in (2) transition to a radius-vector of the electron is carried out really only before collecting of exponents. It is used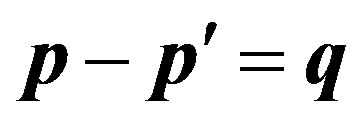 —the law of conservation of an impulse of the electron,
—the law of conservation of an impulse of the electron, 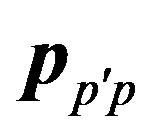 is a matrix element of an impulse of the electron in a field of a nucleus, so
is a matrix element of an impulse of the electron in a field of a nucleus, so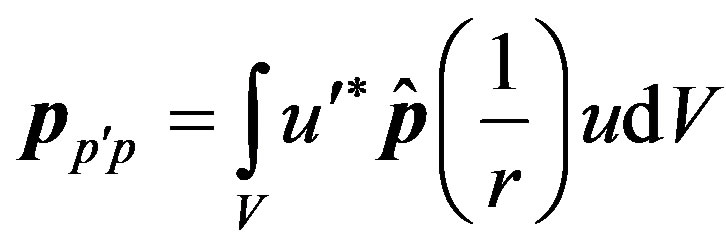 .
.
Wave functions of the electron before and after scattering are accepted as 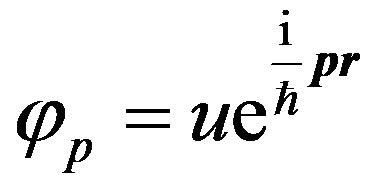 and
and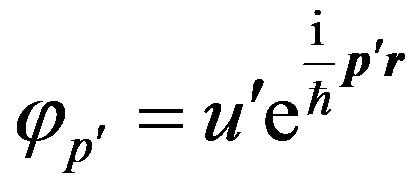 , where u and
, where u and 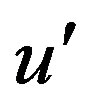 is amplitudes of wave functions. In transformations (2) the formula of the vector analysis
is amplitudes of wave functions. In transformations (2) the formula of the vector analysis 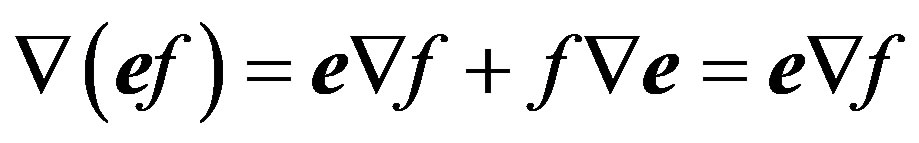 [7] is used.
[7] is used.
For a matrix element of an impulse of the electron we have:
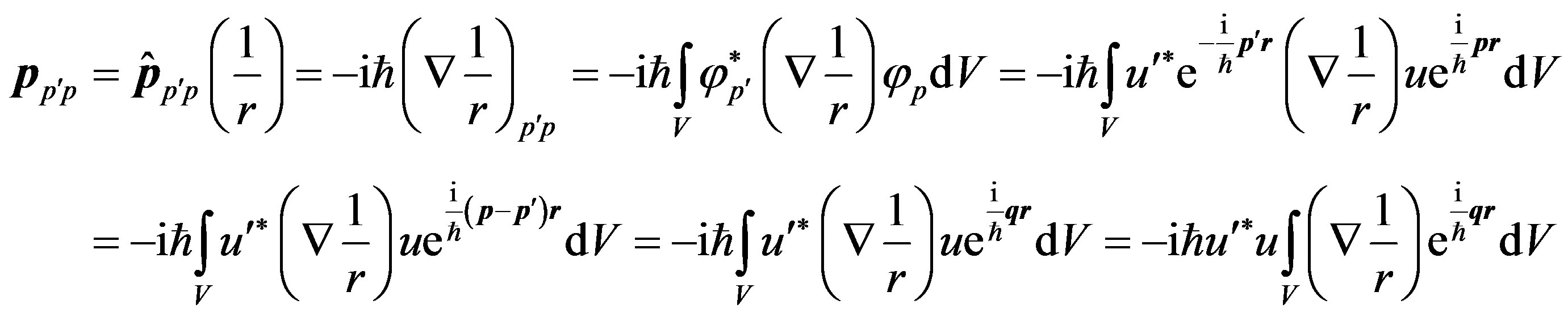 (3)
(3)
Let’s find integral [5,6]:
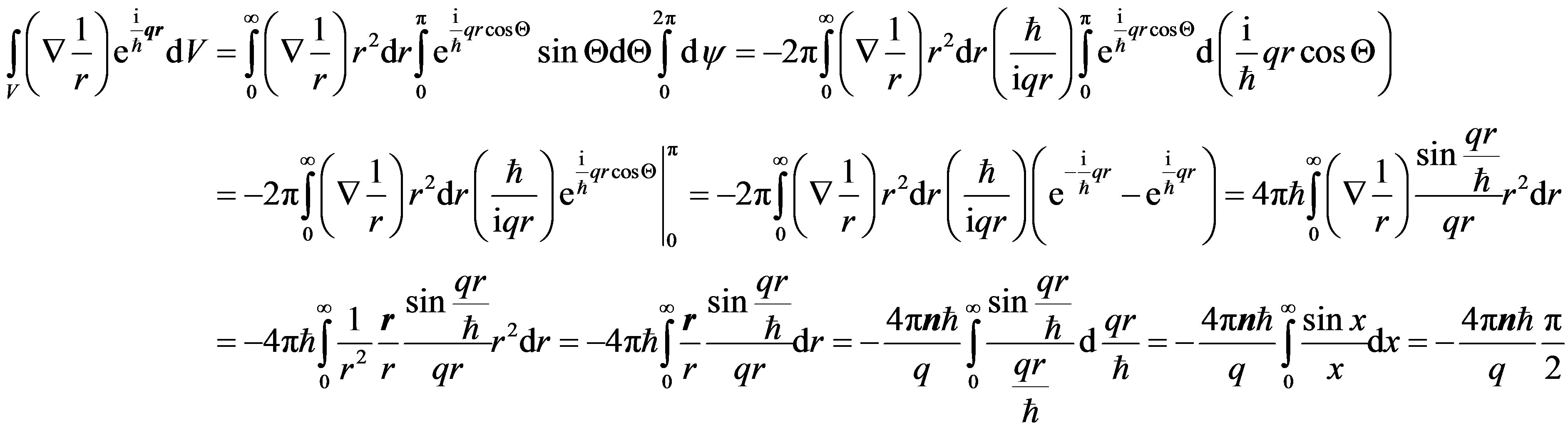
where 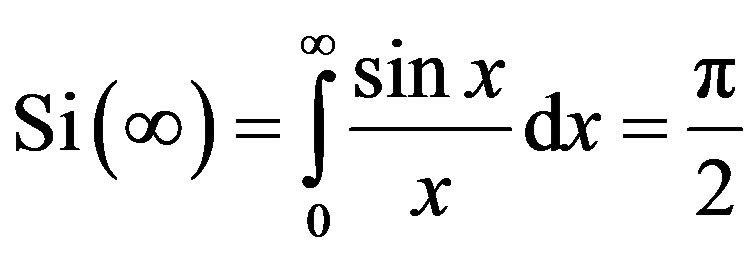 is an integrated sine,
is an integrated sine, 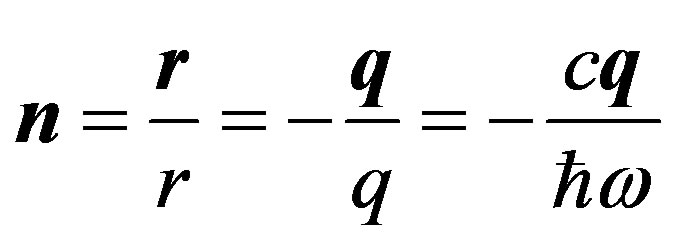 —a unit vector in a direction of a radius-vector of the electron. According to the law of conservation of energy the module
—a unit vector in a direction of a radius-vector of the electron. According to the law of conservation of energy the module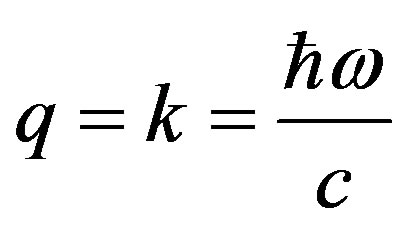 .
.
Hence, the matrix element of an impulse of the electron in a field of a nucleus is equal:
 . (4)
. (4)
where it is accepted, that the quantum starts up radial from atom. Thus the quantum has an impulse k which makes with a vector n angle Q, Figure 1.
Assuming amplitudes of wave functions
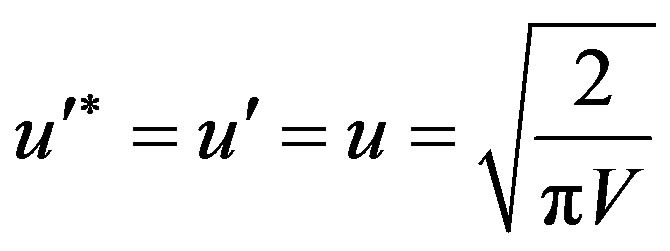 [5], we shall find:
[5], we shall find:
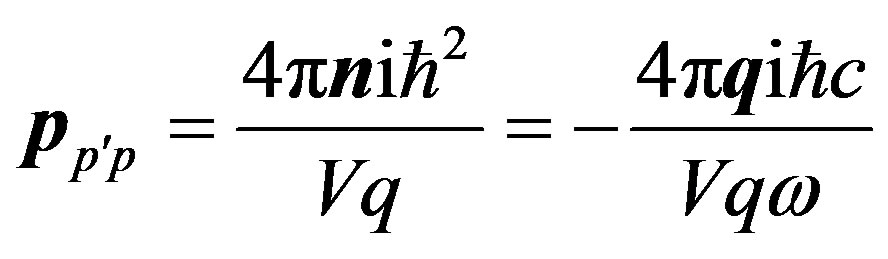 . (5)
. (5)
The probability of transition of the electron  in unit of time with radiation of a photon in a solid angle
in unit of time with radiation of a photon in a solid angle , taking into account (2), is equal [5,6]:
, taking into account (2), is equal [5,6]:
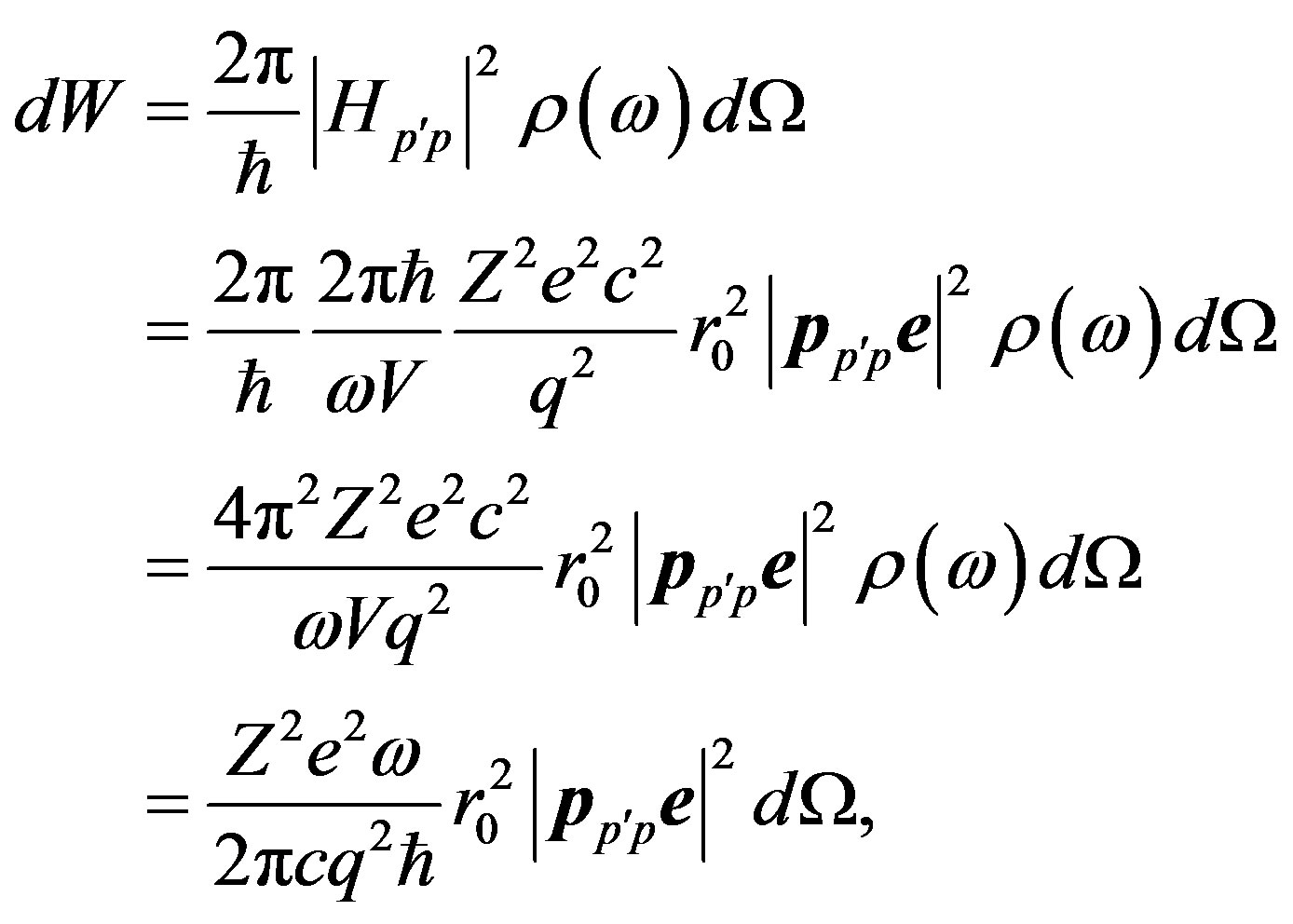 (6)
(6)
where the number of photons in volume V, falling in unit power and  angular intervals at the given polarization of a photon looks like
angular intervals at the given polarization of a photon looks like 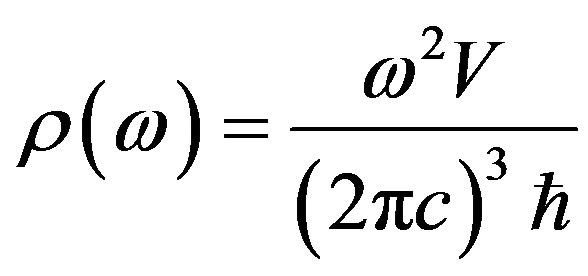 [5].
[5].
For finding of differential effective section of process 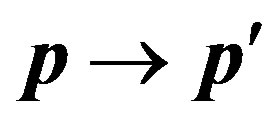 with scattering of the electron in a spatial range of an impulse
with scattering of the electron in a spatial range of an impulse 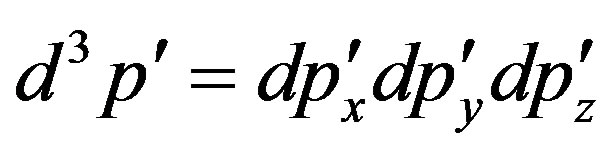 we use the formula [5, 8]:
we use the formula [5, 8]:
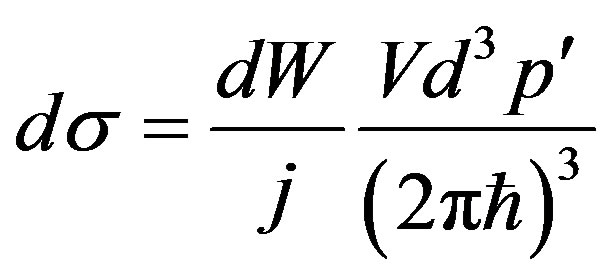 , (7)
, (7)
where  is density of a flux of falling electrons, N—number of falling electrons, v—their speed [5,7]. At
is density of a flux of falling electrons, N—number of falling electrons, v—their speed [5,7]. At 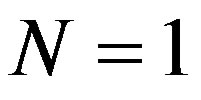 this density of a flux is equal
this density of a flux is equal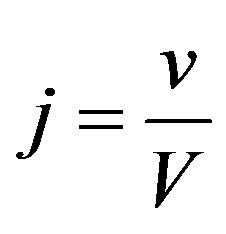 .
.
Substituting (6) in (7), we shall find differential effective section of process of transition of the electron 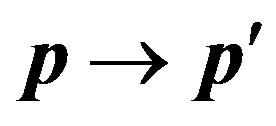 :
:
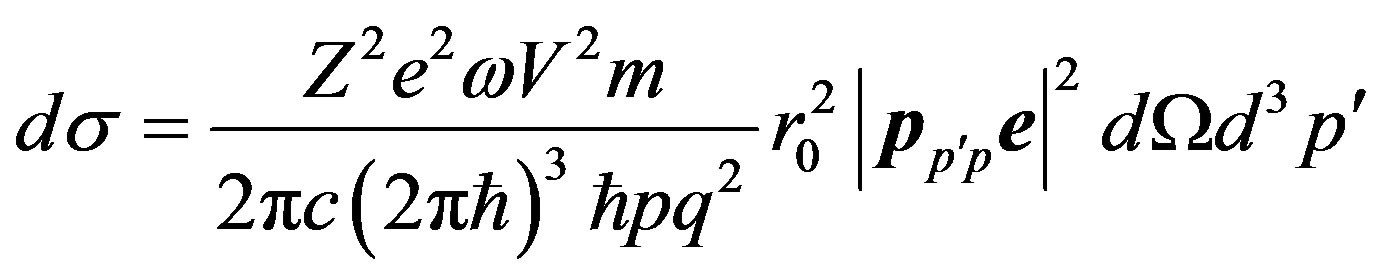 , (8)
, (8)
where it is taken into account, that an impulse of the electron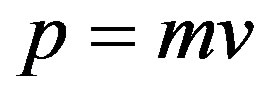 .
.
At scattering of the electron in a solid angle do:
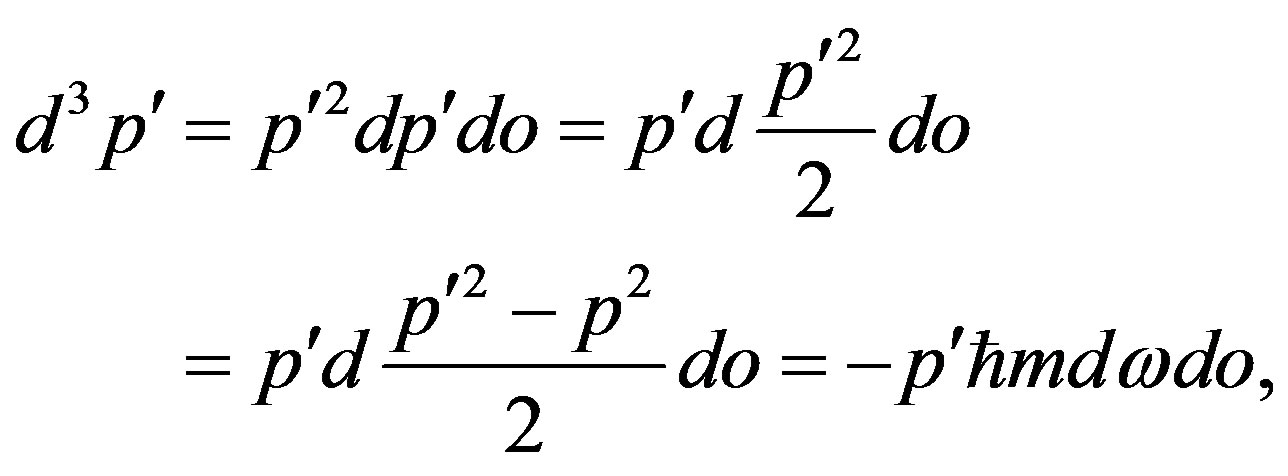 (9)
(9)
where the law of conservation of energy as
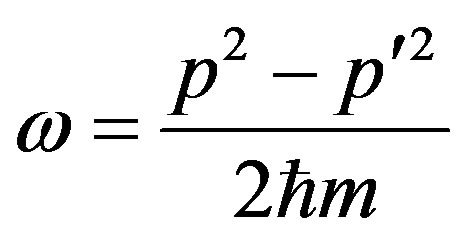 and a condition
and a condition 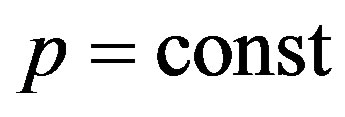 is used.
is used.
Substituting (9) in (8), and taking into account positive value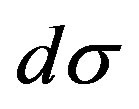 , we have:
, we have:
 . (10)
. (10)
Substituting (5) in (10), we shall transform effective section of process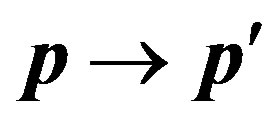 :
:
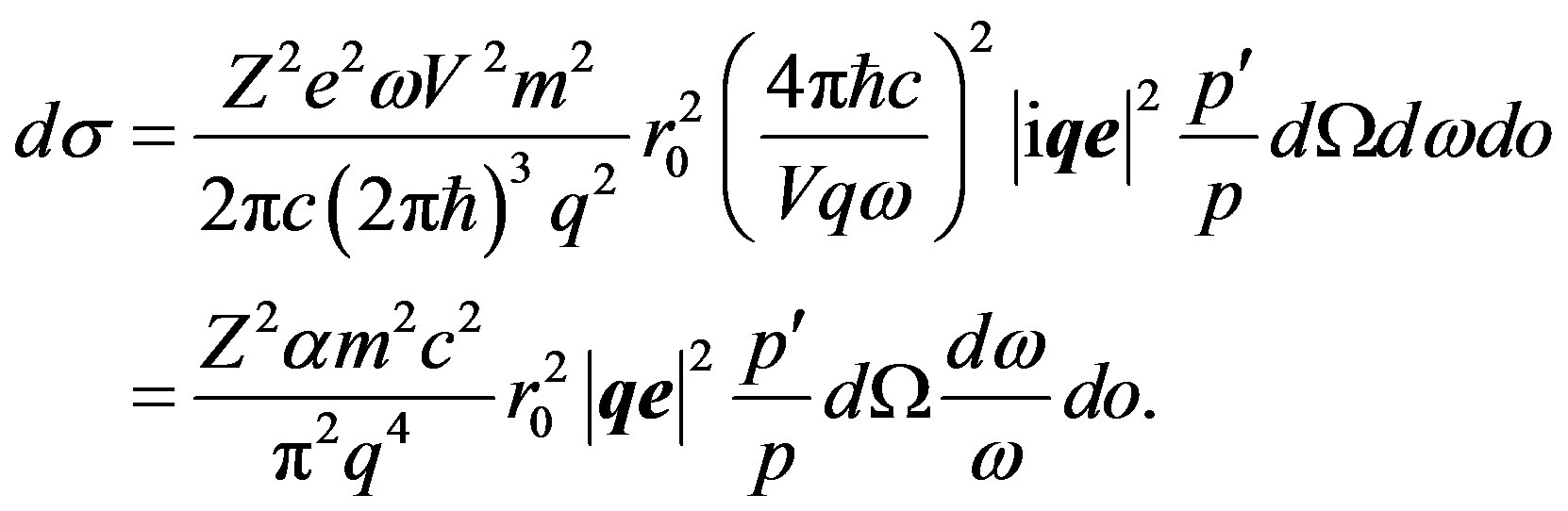 (11)
(11)
where 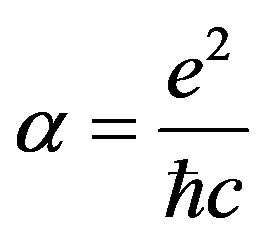 is a fine-structure constant.
is a fine-structure constant.
The received formula coincides with [8] where it is deduced by other, more formal way.
In a direction 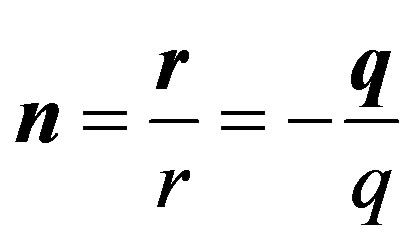 quanta do not take offsince in this case
quanta do not take offsince in this case 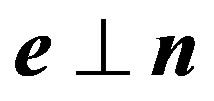 and
and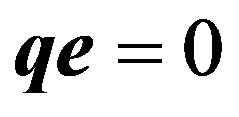 . In a direction perpendicular n the probability of a start of quantum is maximal. Distribution of probability of a start of quanta is shown in Figure 1. The same conclusion is made in [9].
. In a direction perpendicular n the probability of a start of quantum is maximal. Distribution of probability of a start of quanta is shown in Figure 1. The same conclusion is made in [9].
Let’s lead integration in directions of a photon k and in directions of polarization.
Assuming dipole character of radiation of quanta, we have, that distribution of intensity of the taken off quantums submits to the law 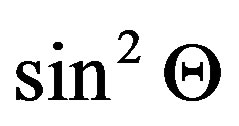 [7].
[7].
Integration on directions of polarization is reduced only to multiplication 2 since exist two directions of polarization. Taking into account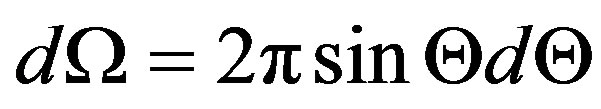 , we shall find:
, we shall find:
 (12)
(12)
Further we shall integrate in directions of scattering of electron q. Taking into account 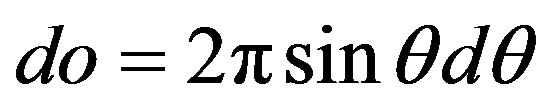 and
and , we have:
, we have:
 (13)
(13)
The formula (13) characterizes spectral distribution of differential effective section of braking and scattering of electrons.
The differential effective section of scattering of electrons is connected to numerical intensity 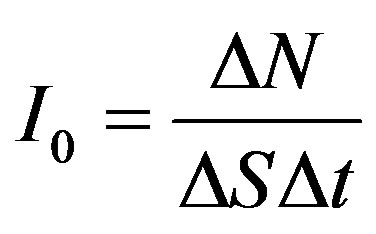 of a falling flux of electrons under the formula
of a falling flux of electrons under the formula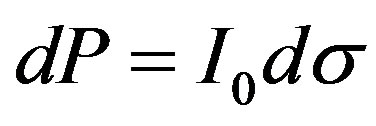 , where dP—differential of a flux of a scattering electrons. Taking into account, that each scattering electron generates one quantum of brake radiation, it is possible to assume, that
, where dP—differential of a flux of a scattering electrons. Taking into account, that each scattering electron generates one quantum of brake radiation, it is possible to assume, that 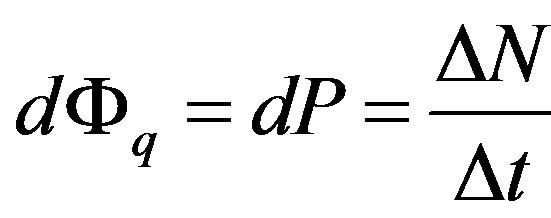 is a numerical flux of quantums of brake radiation.
is a numerical flux of quantums of brake radiation.
Hence:
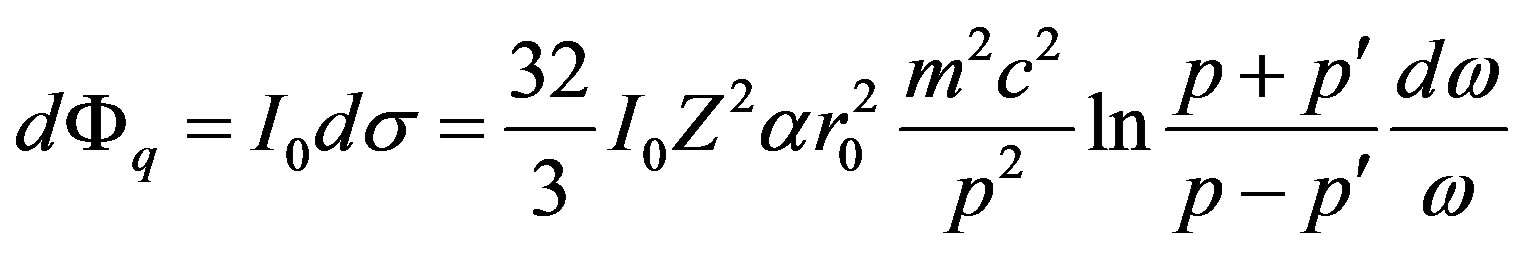 . (14)
. (14)
The energy flux of quanta of radiation is equal:
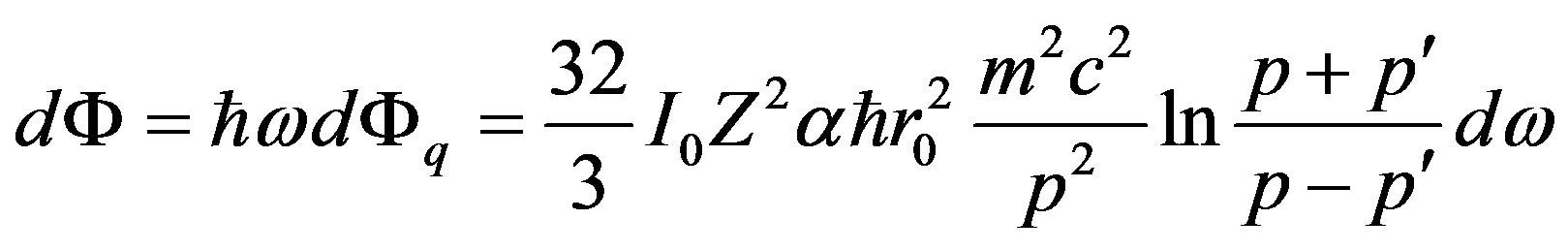 . (15)
. (15)
Hence, the spectral density of a flux of photons 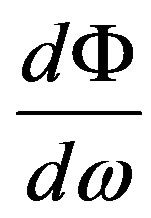
does not depend on frequency that coincides with a conclusion [10].
Let’s note, that the received formula (15) does not take into account shielding a field of a nucleus by atom’s electrons. The account of effect of shielding is usually carried out by introduction empirical and half-empirical amendments [2].
Integrating (15) in limits from 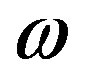 up to
up to —the greatest possible frequency of a photon, we shall find dependence of a flux of quanta of brake radiation on frequency:
—the greatest possible frequency of a photon, we shall find dependence of a flux of quanta of brake radiation on frequency:
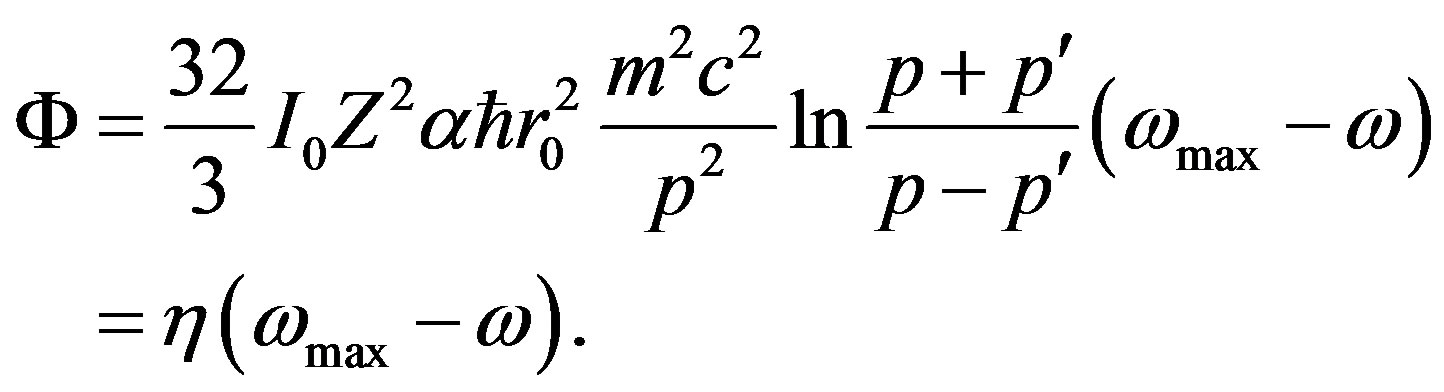 (16)
(16)
where  is the factor dependent on a kind of a biotissue (charging number of nucleus Z), numerical intensity of a flux
is the factor dependent on a kind of a biotissue (charging number of nucleus Z), numerical intensity of a flux 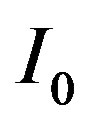 of electrons falling on a biotissue, impulses of electrons before р and after
of electrons falling on a biotissue, impulses of electrons before р and after 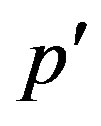 interaction with nucleus. The maximal possible frequency of brake radiation can be found under the formula
interaction with nucleus. The maximal possible frequency of brake radiation can be found under the formula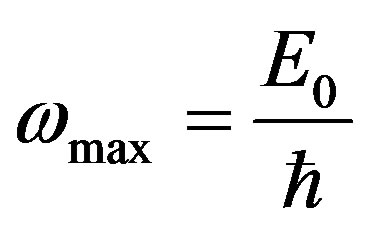 , where
, where 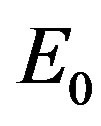 is the maximal energy of electrons in a spectrum β-particles. It is supposed, that all energy of the electron transform in energy of quantum of electromagnetic radiation.
is the maximal energy of electrons in a spectrum β-particles. It is supposed, that all energy of the electron transform in energy of quantum of electromagnetic radiation.
If to accept kinetic energy of the falling electron as
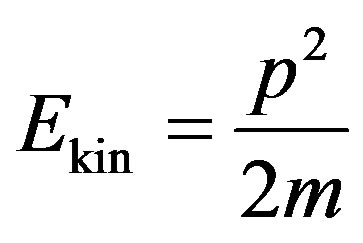 the value
the value 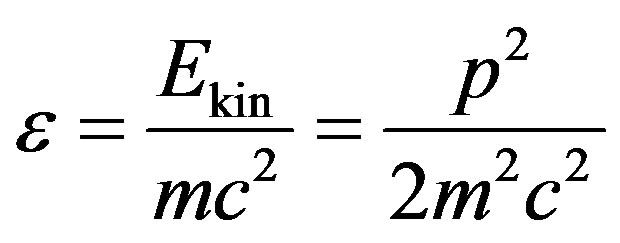 will represent a fraction of kinetic energy of the electron in its full energy. Hence
will represent a fraction of kinetic energy of the electron in its full energy. Hence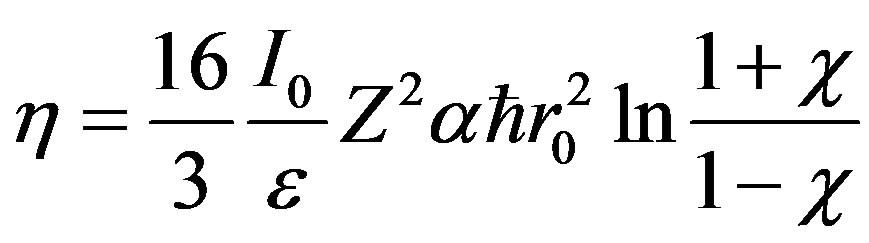 , where
, where
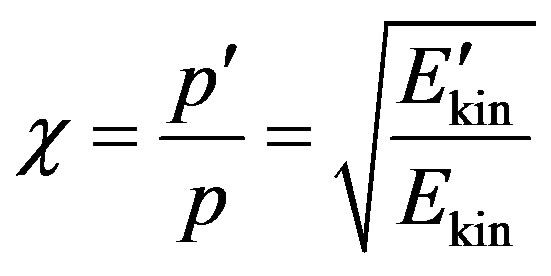 is the parameter describing efficiency of braking of electrons by a biotissue on one atom of substance,
is the parameter describing efficiency of braking of electrons by a biotissue on one atom of substance,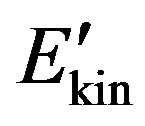 —kinetic energy of the electron after interaction with atom. At
—kinetic energy of the electron after interaction with atom. At 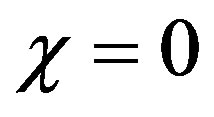 braking full, at
braking full, at  braking is absent. Size of linear energy transfer for electrons is
braking is absent. Size of linear energy transfer for electrons is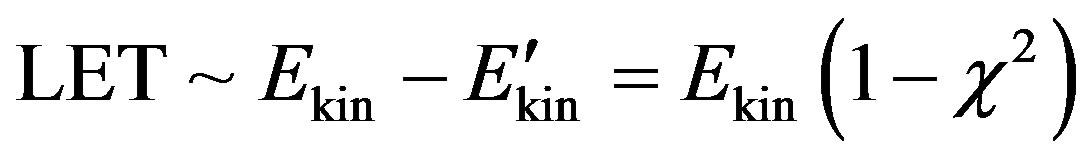 .
.
On Figure 2 dependence of relative factor
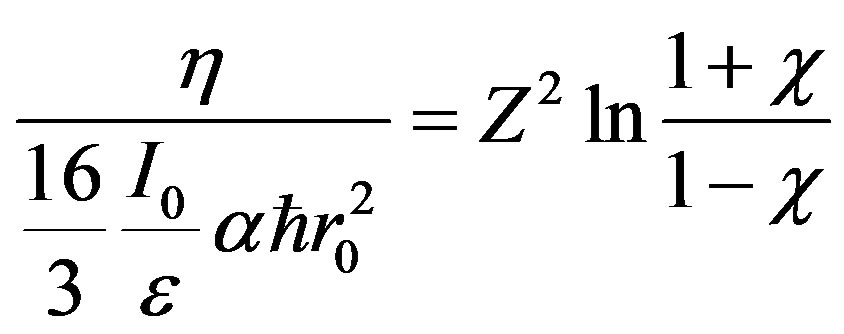 on parameter of efficiency of braking
on parameter of efficiency of braking 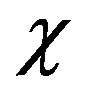 for various elements of a biotissue is shown. At small values of parameter of efficiency of braking dependence has practically linear character.
for various elements of a biotissue is shown. At small values of parameter of efficiency of braking dependence has practically linear character.
3. THE RELATIVISTIC AMENDMENT
Let’s consider influence of relativistic effects on character of brake radiation.
Let E is initial energy of the electron falling on the substance.
There is a probability of radiation of a photon at movement of the electron in a field of atom. The law of conservation of energy looks like:
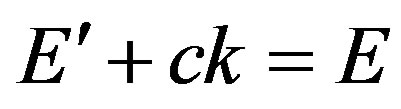 , (17)
, (17)
where 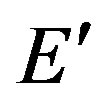 is final energy of the electron.
is final energy of the electron.
During movement of the electron transition of system atom-electron from an initial condition 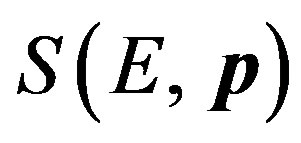 (start) in a final condition
(start) in a final condition 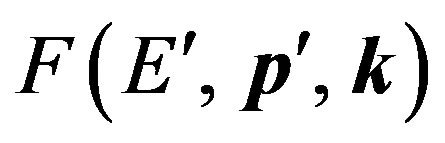 (finish) is carried out. Hamiltonian interactions are equal:
(finish) is carried out. Hamiltonian interactions are equal:
 , (18)
, (18)
where Hamiltonian is conditionally separated into two addends. The first addend 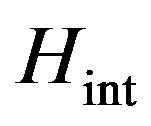 characterizes radiation by the electron of the quantum, the second addend V— interaction of the electron with a field of atom.
characterizes radiation by the electron of the quantum, the second addend V— interaction of the electron with a field of atom.
In a case Coulomb’s field the energy of interaction of the electron and atom looks like:

Figure 2. Calculate dependence of relative size of value h on parameter of efficiency of braking of β-electrons and charging number of elements of a biotissue in not relativistic case.
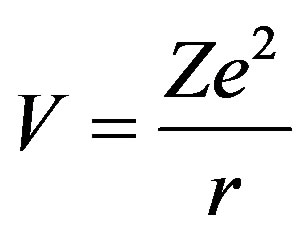 . (19)
. (19)
Transition 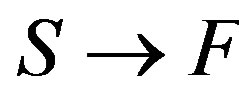 occurs through intermediate states. Two types of transitions and, accordingly, two intermediate states I and II are possible.
occurs through intermediate states. Two types of transitions and, accordingly, two intermediate states I and II are possible.
1) At transition of system in the first intermediate state 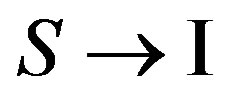 the electron with an impulse
the electron with an impulse  radiates a photon a pulse k. After that the electron has an impulse
radiates a photon a pulse k. After that the electron has an impulse . The law of conservation of an impulse looks like:
. The law of conservation of an impulse looks like:
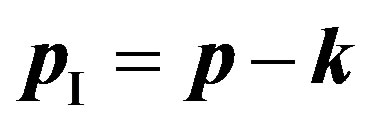 . (20)
. (20)
Transition 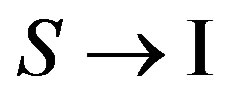 is determined addend
is determined addend  in Hamiltonian (18).
in Hamiltonian (18).
Square of energy of the electron in the first intermediate state , where
, where 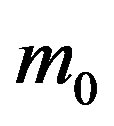 is mass of rest of the electron.
is mass of rest of the electron.
Then the electron transits in a final state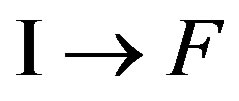 . This transition is determined addend V in Hamiltonian (18). Change of an impulse of the electron looks like:
. This transition is determined addend V in Hamiltonian (18). Change of an impulse of the electron looks like:
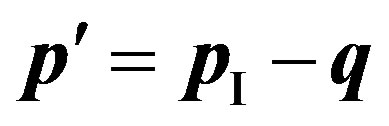 , (21)
, (21)
where  is a part of an impulse of the electron, transmitted to atom to which there is an interaction.
is a part of an impulse of the electron, transmitted to atom to which there is an interaction.
2) If the system transit in the second intermediate state , the electron, due to interaction with atom, preliminary loses a part of an impulse. Its impulse
, the electron, due to interaction with atom, preliminary loses a part of an impulse. Its impulse 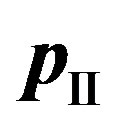 to become equal:
to become equal:
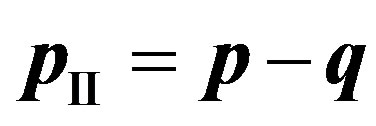 . (22)
. (22)
This transition is determined addend V in Hamiltonian (18).
Square of energy of the electron in the second intermediate state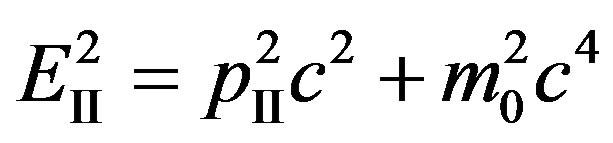 .
.
Then, at transition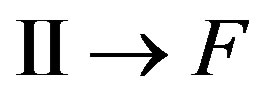 , the electron radiates a photon an impulse k, transits in a final state with an impulse
, the electron radiates a photon an impulse k, transits in a final state with an impulse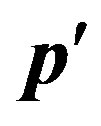 :
:
 . (23)
. (23)
Transition 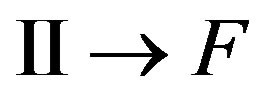 is determined addend
is determined addend 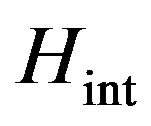 in Hamiltonian (18).
in Hamiltonian (18).
Combining (20) and (21) or (22) and (23) we notice, that in both cases the law of conservation of an impulse at transition  looks like:
looks like:
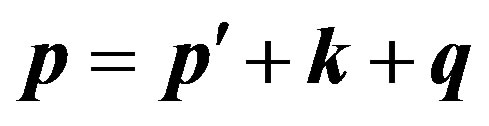 , (24)
, (24)
i.e. the part of an initial impulse of the electron 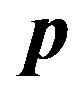 is transferred to a photon
is transferred to a photon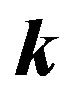 , and other part
, and other part  is transferred to atom. Therefore the size
is transferred to atom. Therefore the size  is identical to the first and second variants of transition.
is identical to the first and second variants of transition.
Let’s find a matrix element of that part of interaction of the electron with atom 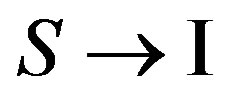 in which occurs emission of a photon by an impulse k.
in which occurs emission of a photon by an impulse k.
Research of process of transition of the electron in an intermediate state 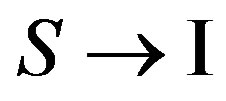 rather simple in connection with linearity of the operator of Hamilton concerning value
rather simple in connection with linearity of the operator of Hamilton concerning value , where р is an impulse of the electronе—a charge of the electron, c—speed of light in vacuum, A is vector-potential of a photon. At a transit
, where р is an impulse of the electronе—a charge of the electron, c—speed of light in vacuum, A is vector-potential of a photon. At a transit 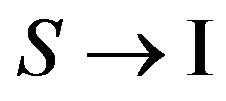 we do not take into account presence of atom. At use of Coulombian calibrations of potentials, we have [5,7]:
we do not take into account presence of atom. At use of Coulombian calibrations of potentials, we have [5,7]:
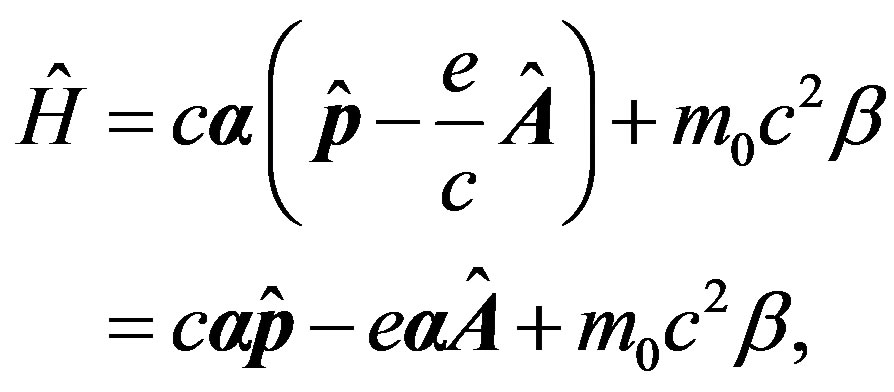 (25)
(25)
where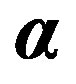 —so-called a matrix vector (a vector, whose coordinate projections are square matrixes of 4th order, with components 0, ±1, ±i),
—so-called a matrix vector (a vector, whose coordinate projections are square matrixes of 4th order, with components 0, ±1, ±i), —a square matrix of 4th order with components 0, ±1 [5]. All multipliers of a matrix vector
—a square matrix of 4th order with components 0, ±1 [5]. All multipliers of a matrix vector 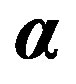 are four-vectors, at which fourth component is imaginary [5]. Energy of interaction the photon-electron characterizes only the second addend (25)i.e. the operator
are four-vectors, at which fourth component is imaginary [5]. Energy of interaction the photon-electron characterizes only the second addend (25)i.e. the operator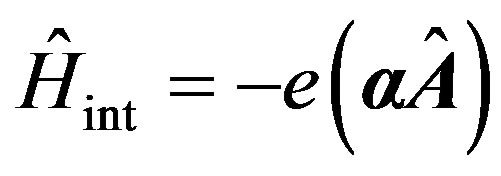 . In connection with that presence of atom is not taken into account yet, in (25), as against (1), it is supposed, that the vector-potential of a photon is periodic, but not radiating function of coordinates
. In connection with that presence of atom is not taken into account yet, in (25), as against (1), it is supposed, that the vector-potential of a photon is periodic, but not radiating function of coordinates . Therefore it is possible to write down Hamiltonian interactions radiated photonelectron as:
. Therefore it is possible to write down Hamiltonian interactions radiated photonelectron as:
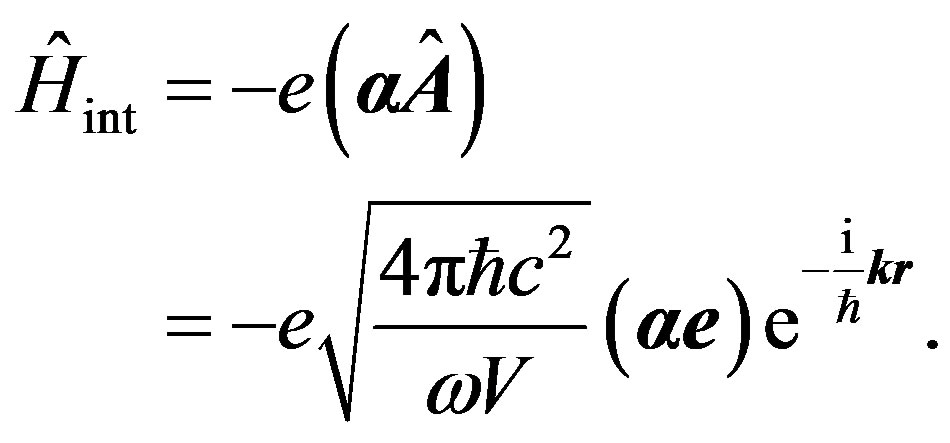 (26)
(26)
The matrix element of transition of states of the electron 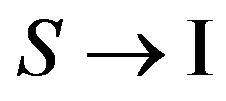 looks like:
looks like:
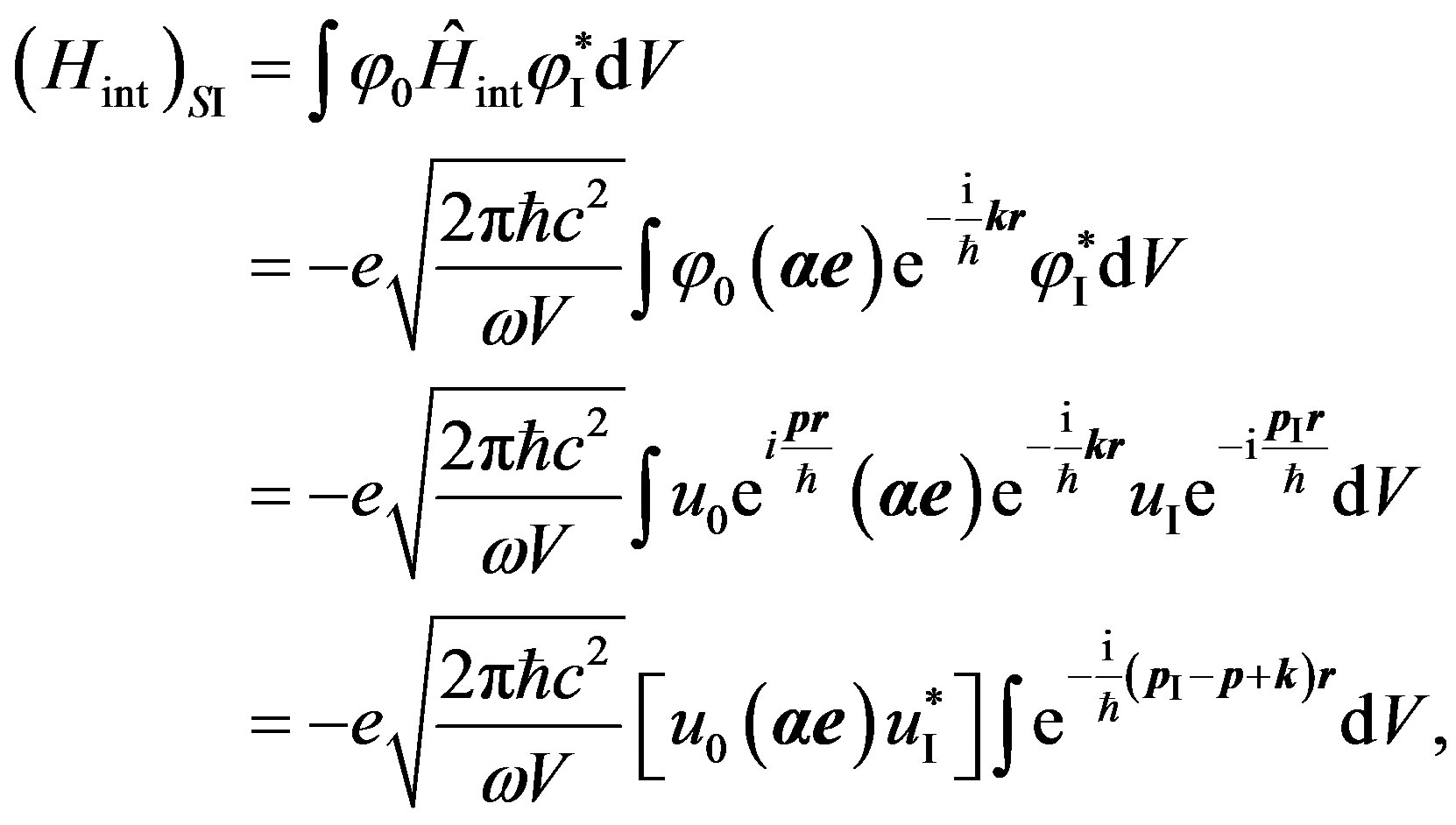 (27)
(27)
where 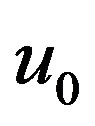 is amplitude of wave function of the electron
is amplitude of wave function of the electron
 in an initial state of the electron. After radiation of a photon we assume, that position of the electron has not changed,
in an initial state of the electron. After radiation of a photon we assume, that position of the electron has not changed,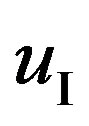 —amplitude of wave function
—amplitude of wave function
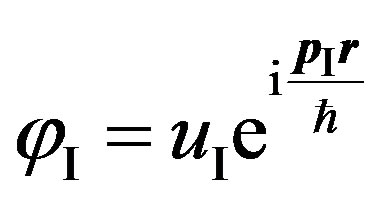 in intermediate state I,
in intermediate state I, —the conjugate amplitude of this wave function.
—the conjugate amplitude of this wave function.
Taking into account the law of conservation of an impulse (20), we have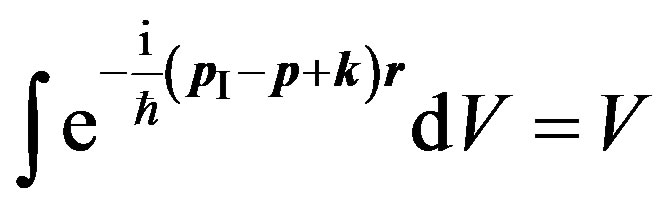 . Assuming normalizing volume
. Assuming normalizing volume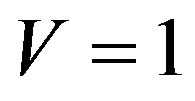 , we shall find a matrix element of transition
, we shall find a matrix element of transition :
:
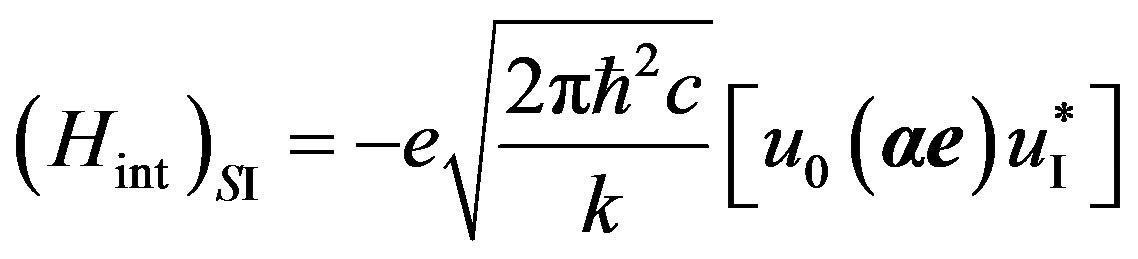 . (28)
. (28)
Let’s find a matrix element 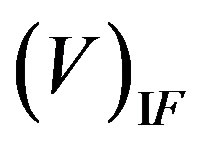 of that part of interaction of the electron with atom
of that part of interaction of the electron with atom  which occurs without emission of a photon. We shall assume, that energy of interaction of the electron and atom has essential value only near to atom, i.e. at r close to zero. At
which occurs without emission of a photon. We shall assume, that energy of interaction of the electron and atom has essential value only near to atom, i.e. at r close to zero. At 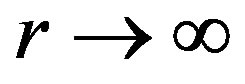 a matrix element is
a matrix element is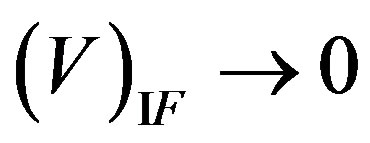 . This position, actually Born’s approximation, will be taken into account at the further conclusion. Far from atom wave functions of the electron are flat waves
. This position, actually Born’s approximation, will be taken into account at the further conclusion. Far from atom wave functions of the electron are flat waves 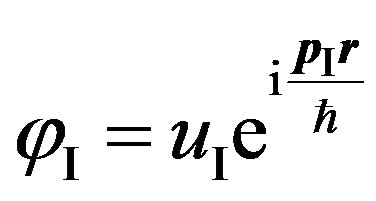 and
and , where u is amplitude of wave function of the electron in a final state.
, where u is amplitude of wave function of the electron in a final state.
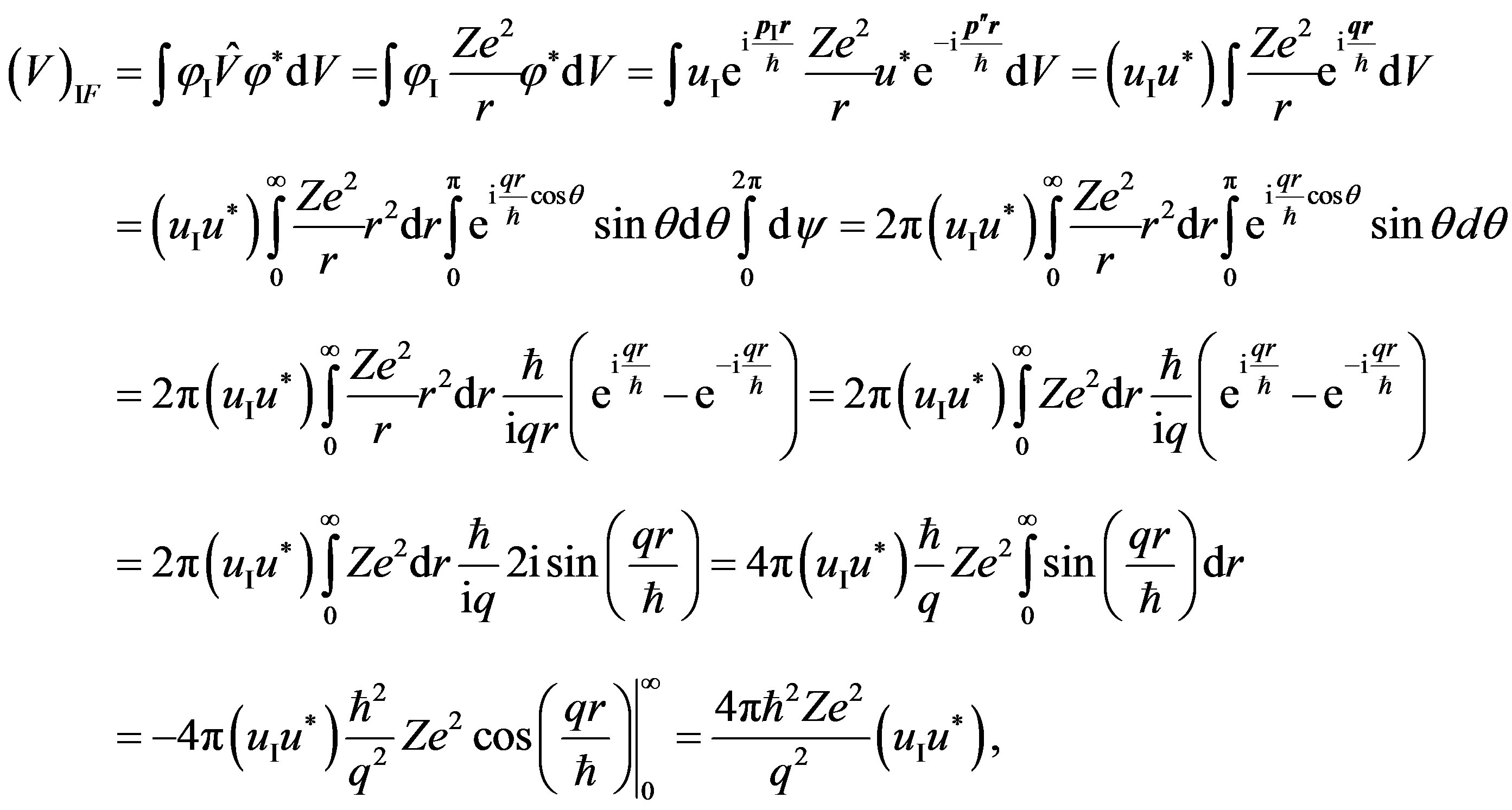 (29)
(29)
where in this case angle  is between radius-vector of the electron
is between radius-vector of the electron  and a vector of an impulse
and a vector of an impulse , transferred to a nucleus. The law of conservation of an impulse (21) is used. At integration (29) transition to spherical coordinates is lead. Oscillations of a matrix element far from atom at
, transferred to a nucleus. The law of conservation of an impulse (21) is used. At integration (29) transition to spherical coordinates is lead. Oscillations of a matrix element far from atom at  as not having physical sense, neglected.
as not having physical sense, neglected.
At transition in an intermediate state II on nonradiating stage  the matrix element of transition with the account (22) looks like:
the matrix element of transition with the account (22) looks like:
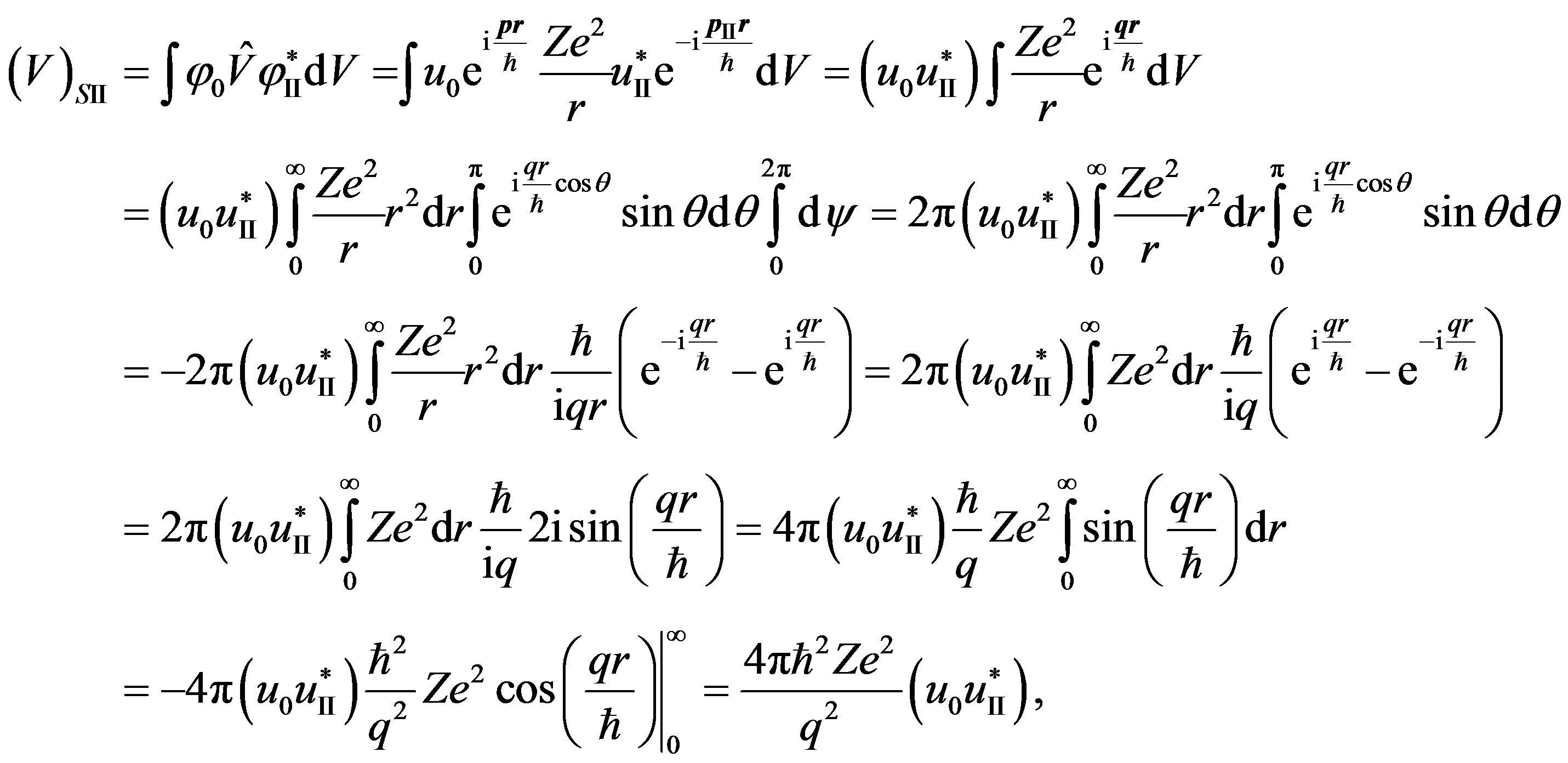 (30)
(30)
where  is the conjugate amplitude of wave function of the electron
is the conjugate amplitude of wave function of the electron 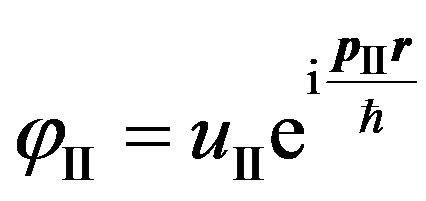 in an intermediate state II.
in an intermediate state II.
To radiating stage 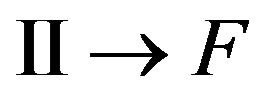 there corresponds a matrix element of transition:
there corresponds a matrix element of transition:
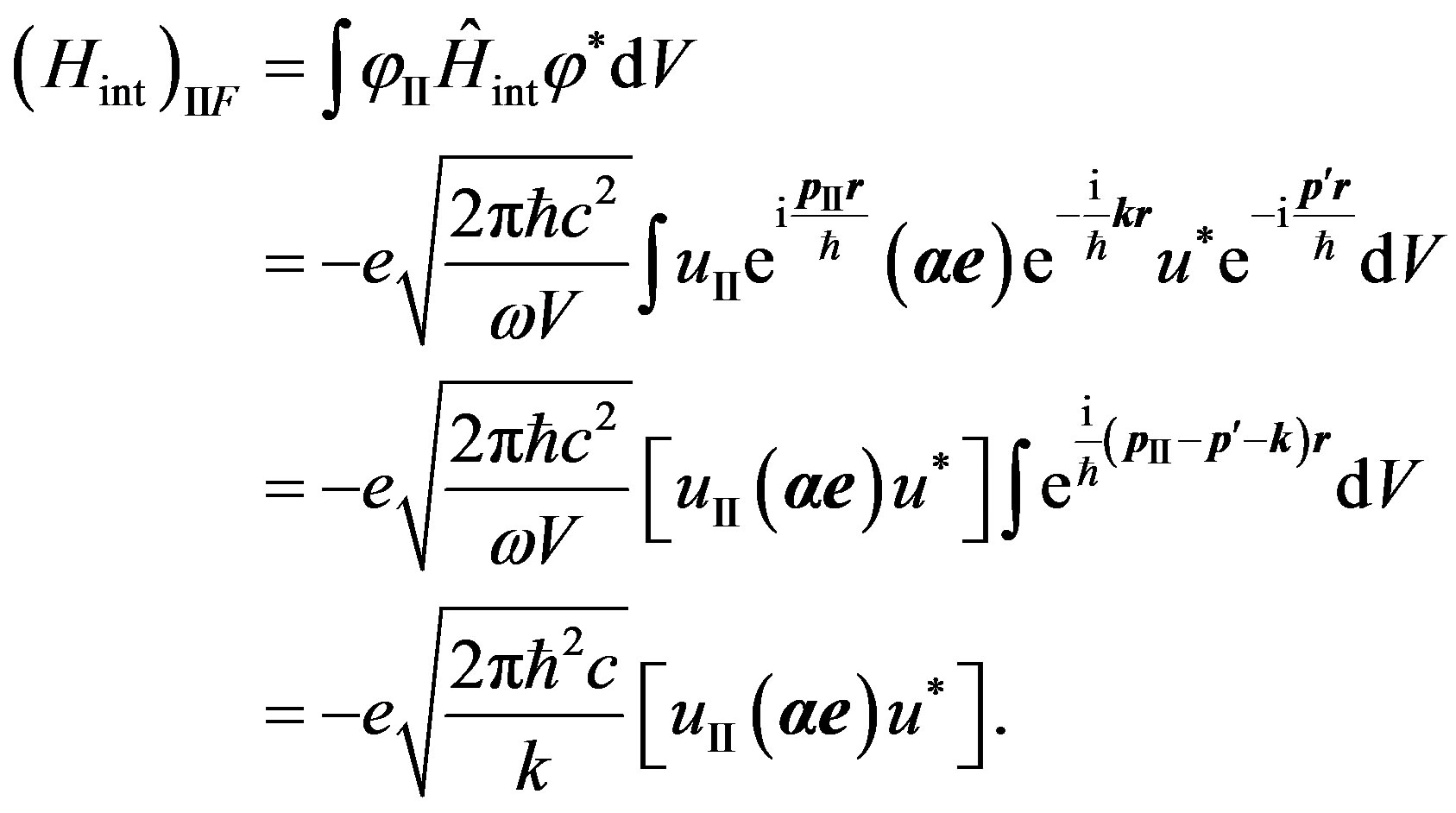 (31)
(31)
Thus the law of conservation of an impulse (23) is used.
The compound matrix element of interaction of the electron and atom looks like:
 . (32)
. (32)
In denominators addends (32) should be differences between energy of an initial condition of system the electron-atom and energy this system in intermediate states I and II. However, in connection with that energy of atom at interaction with the electron is assumed constant, at subtraction in denominators energy of atom disappears and it is possible to not take into account. Therefore in denominators energy of the electron and a photon is taken into account only.
The intermediate state of the electron  arises after emission of a photon, but before interaction with atom, therefore in a denominator of the first addend energy emitted photon is subtracted. The intermediate state of the electron
arises after emission of a photon, but before interaction with atom, therefore in a denominator of the first addend energy emitted photon is subtracted. The intermediate state of the electron 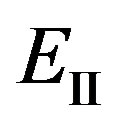 arises due to its interaction with atom before emission of a photon. Therefore in a denominator of the second addend to subtract energy of a photon it is not necessary.
arises due to its interaction with atom before emission of a photon. Therefore in a denominator of the second addend to subtract energy of a photon it is not necessary.
Taking into account (17), we have:
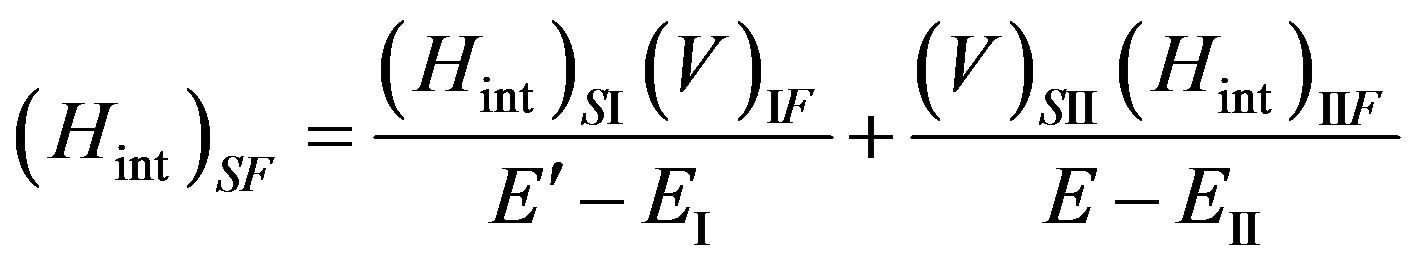 . (33)
. (33)
Let’s substitute in (33) formulas (28)-(31):
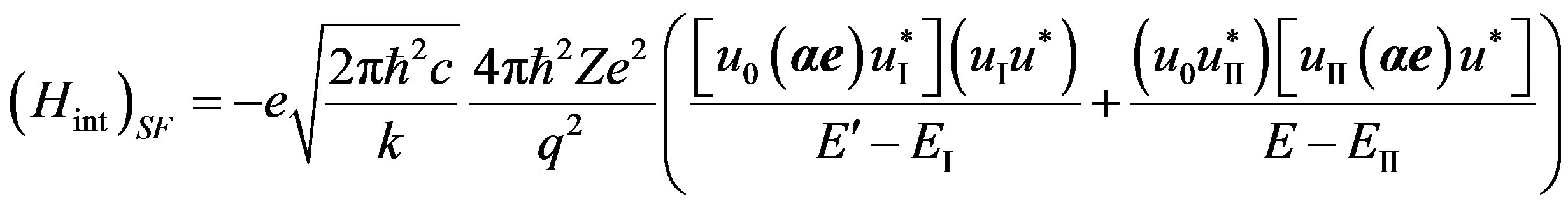 . (34)
. (34)
The probability of transition of system in unit of time 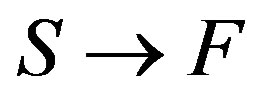 is proportional to a square of a corresponding matrix element [5]:
is proportional to a square of a corresponding matrix element [5]:
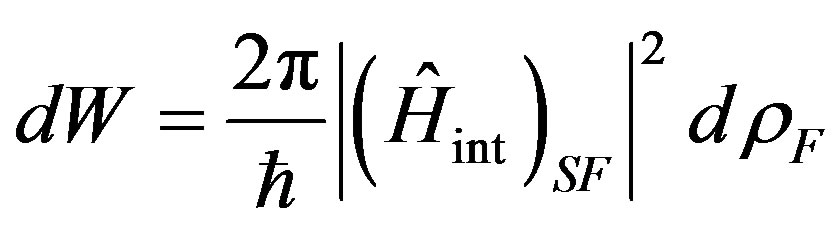 , (35)
, (35)
where 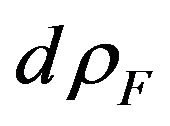 is number of final power states of the system, falling a unit interval of energy
is number of final power states of the system, falling a unit interval of energy 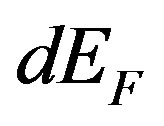 of a final state [9]. At a final state are present the electron with an impulse
of a final state [9]. At a final state are present the electron with an impulse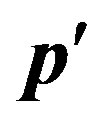 , with energy
, with energy 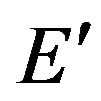 and a photon with an impulse k.
and a photon with an impulse k.
If 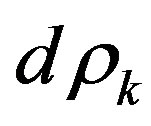 is number of power states of the radiated photon, number of final states of system equally:
is number of power states of the radiated photon, number of final states of system equally:
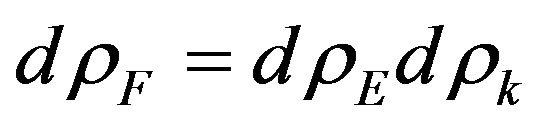 , (36)
, (36)
where 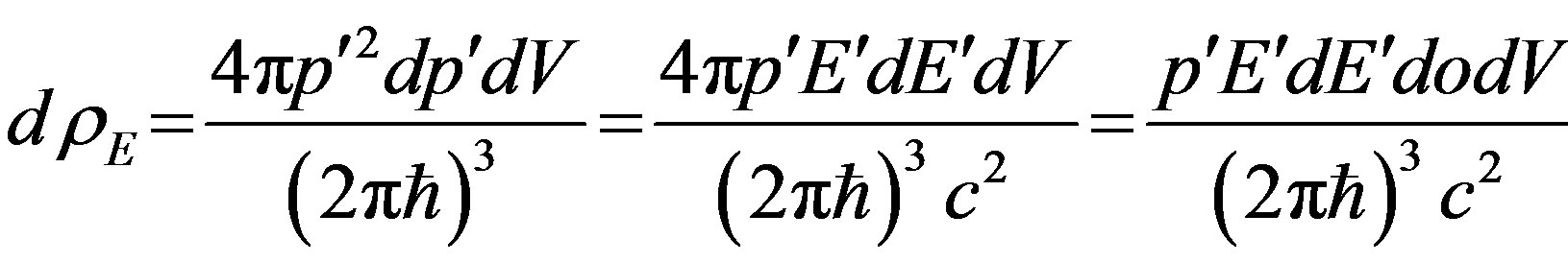 number of power states of the electron [11]. It is taken into account, that energy of the electron
number of power states of the electron [11]. It is taken into account, that energy of the electron
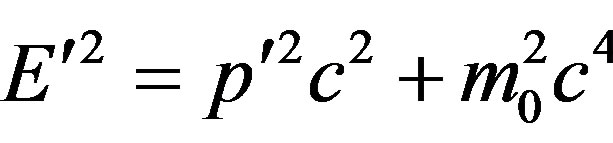 , hence,
, hence, 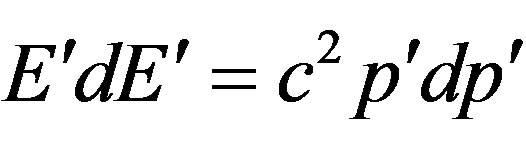 and the fraction of electrons, emitted in a solid angle
and the fraction of electrons, emitted in a solid angle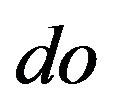 , is equal
, is equal
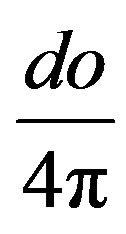 . The density of energy states of electrons in unit interval of energy
. The density of energy states of electrons in unit interval of energy 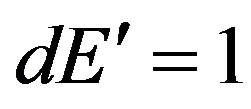 in unit of volume
in unit of volume 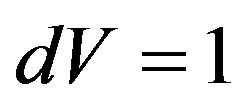 is equal
is equal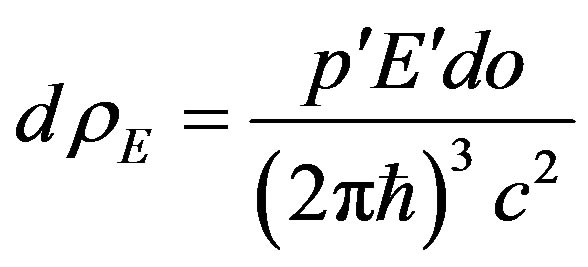 .
.
Number of power conditions of the radiated photon in unit of the volume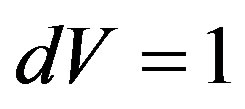 , radiated in a solid angle
, radiated in a solid angle
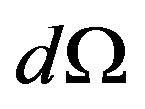 , we find similarly
, we find similarly 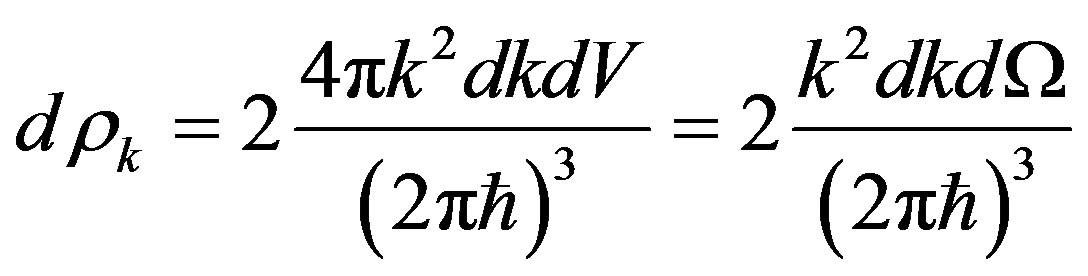
[11]. The factor 2 means two maybe polarizations of a photon.
Hence, number of final states of system equally:
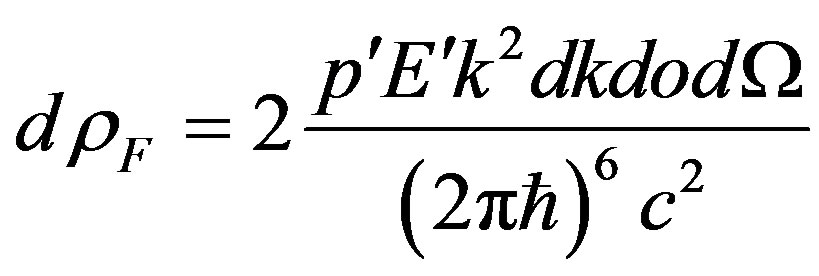 . (37)
. (37)
Let’s substitute (37) in (35):
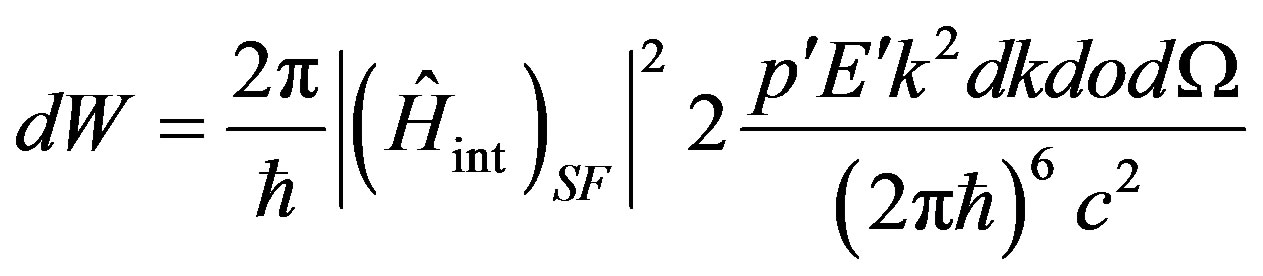 , (38)
, (38)
For finding of differential effective section of process, we shall divide probability of transition in unit of time (38) on numerical density of a flux of falling electrons [5, 8]. One electron is considered, therefore we assume, that in normalizing volume V there is only one electron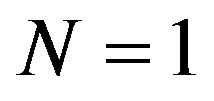 . Therefore the numerical density of a flux of electrons under condition
. Therefore the numerical density of a flux of electrons under condition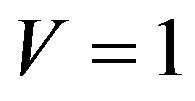 , is equal
, is equal
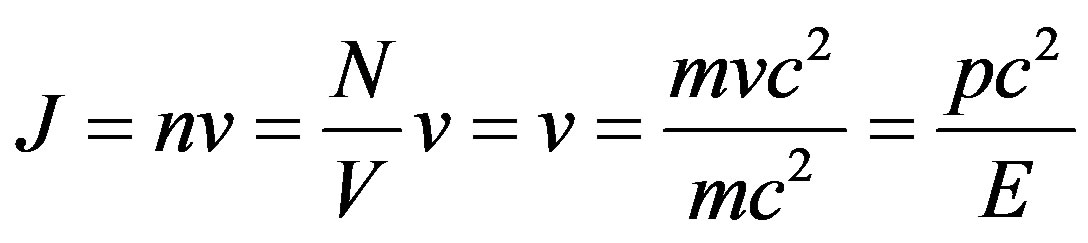 , where m is mass of the moving electron. Hence, differential effective section of process of interaction of the electron and atom looks like:
, where m is mass of the moving electron. Hence, differential effective section of process of interaction of the electron and atom looks like:
 , (39)
, (39)
Substituting in (39) formula (34), we shall find:
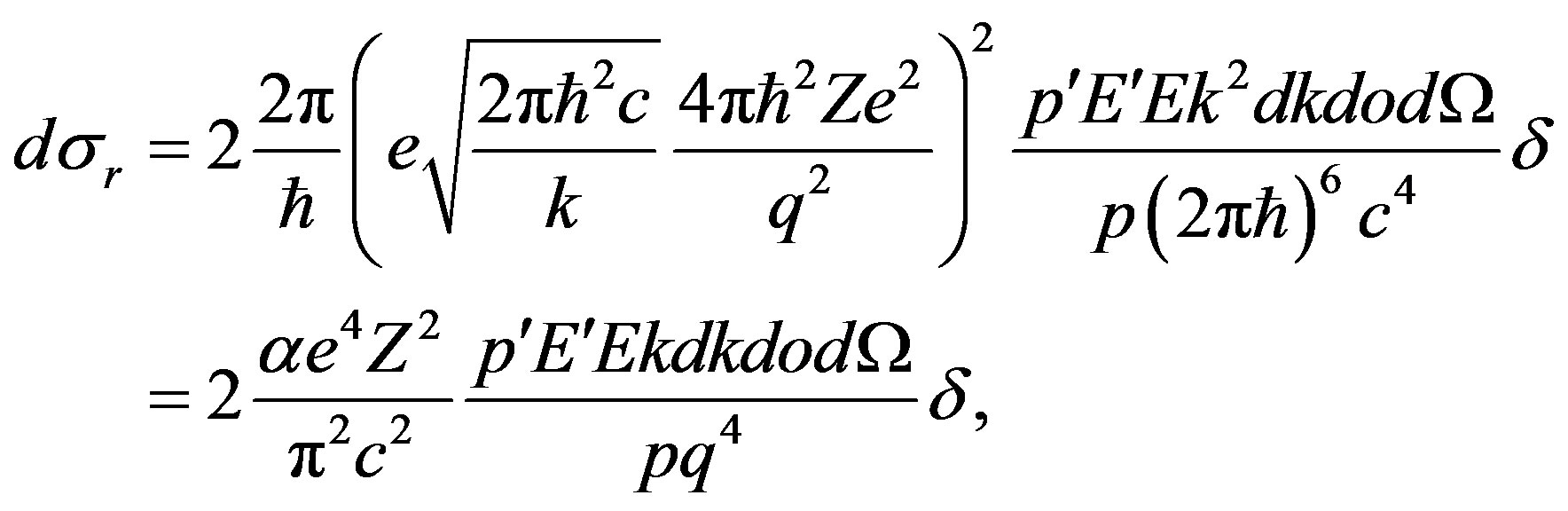 (40)
(40)
where a fine-structure constant is . In (40) it is designated:
. In (40) it is designated:
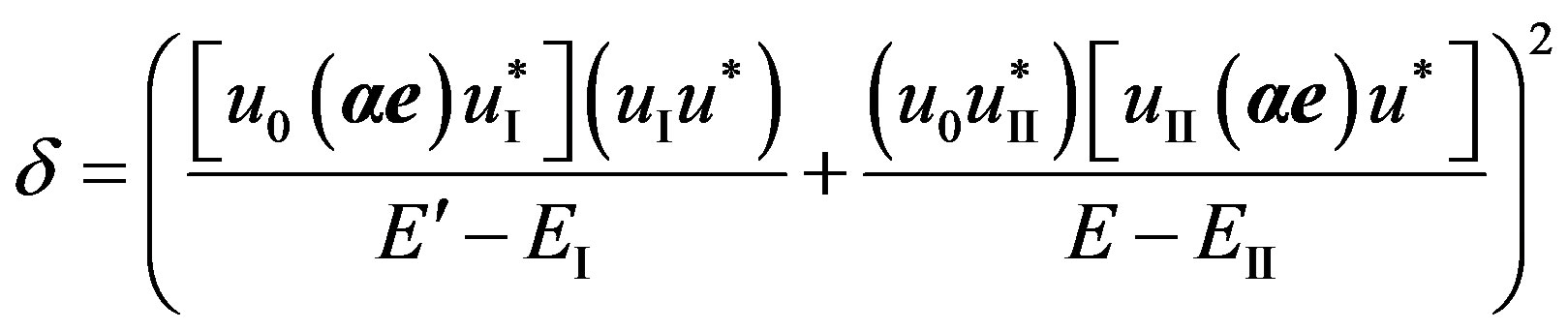 (41)
(41)
Let’s find the ratio of differential effective section of process in relativistic 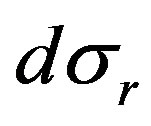 (40) and not relativistic
(40) and not relativistic  (11) kind:
(11) kind:
 (42)
(42)
where 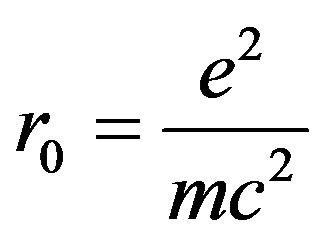 is classical radius of the electron [7].
is classical radius of the electron [7].
Integration in directions of polarization is reduced to multiplication on 2 since exist two directions of polarization and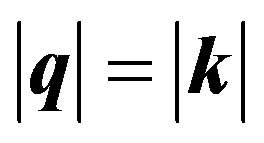 .
.
Hence, taking into account a designation of value d (41), we have:
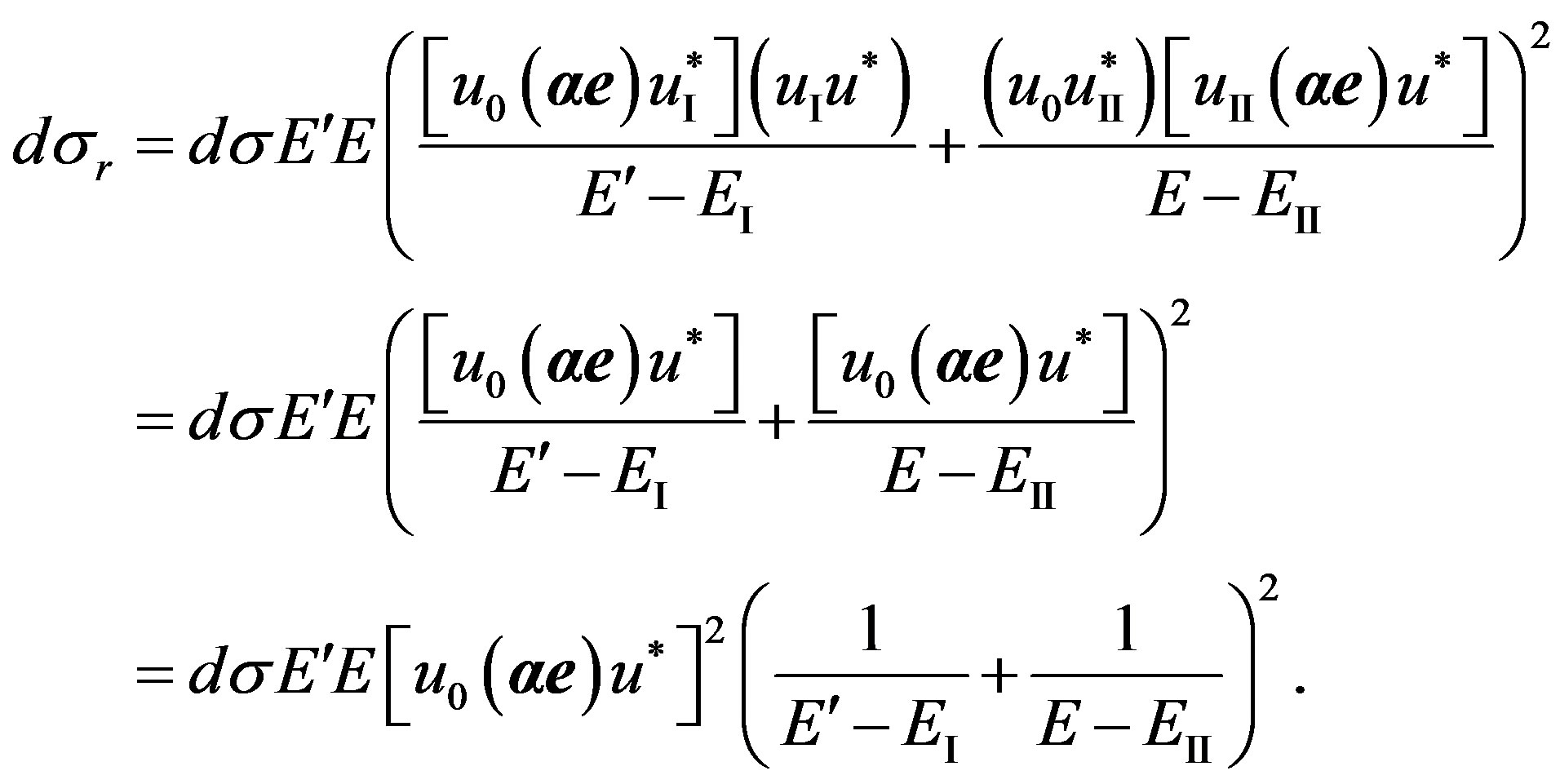 (43)
(43)
As energy of electrons in a ultrarelativistic variant is very great, it is possible to use conditions 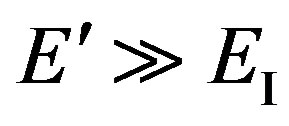 and
and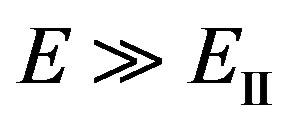 . In this case:
. In this case:
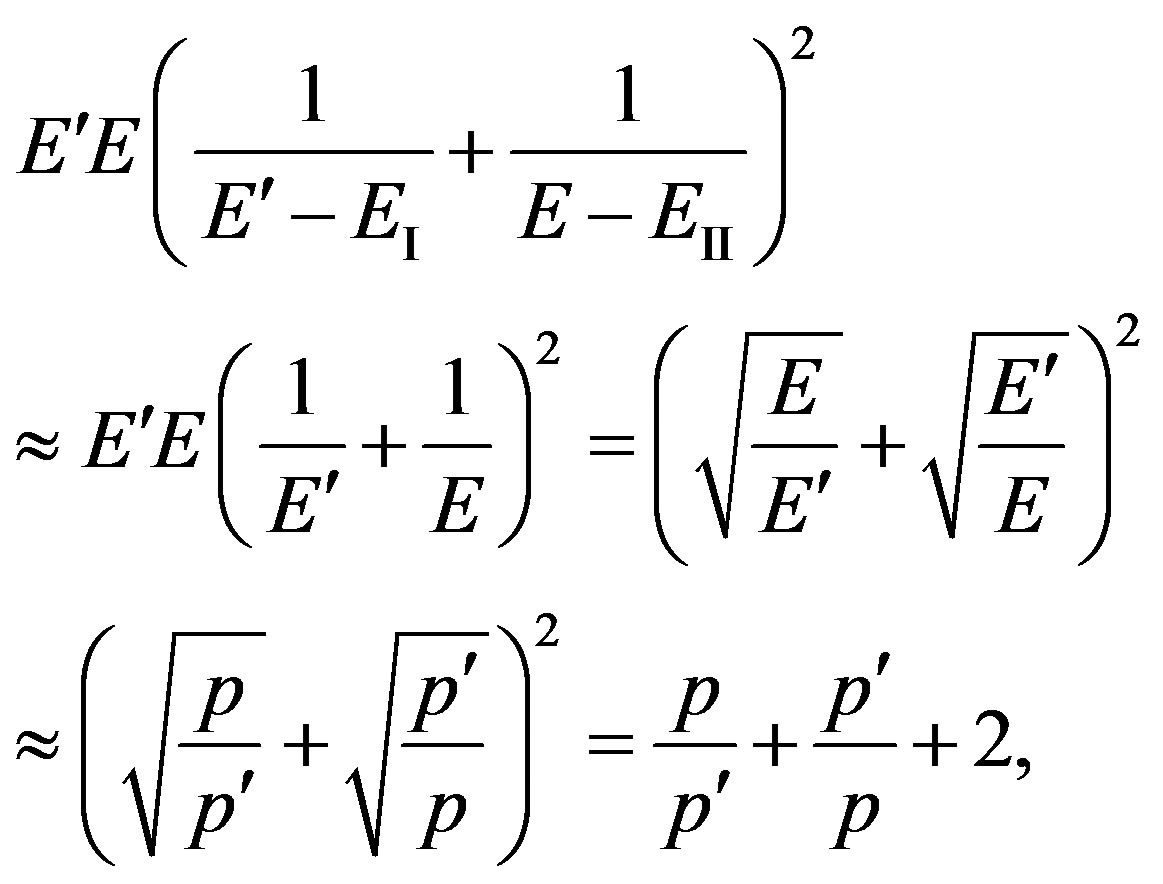
where it is assumed in a ultrarelativistic variant 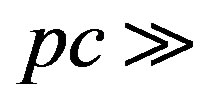
 and, hence
and, hence , and
, and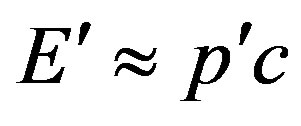 .
.
Hence, the formula (43) will be transformed:
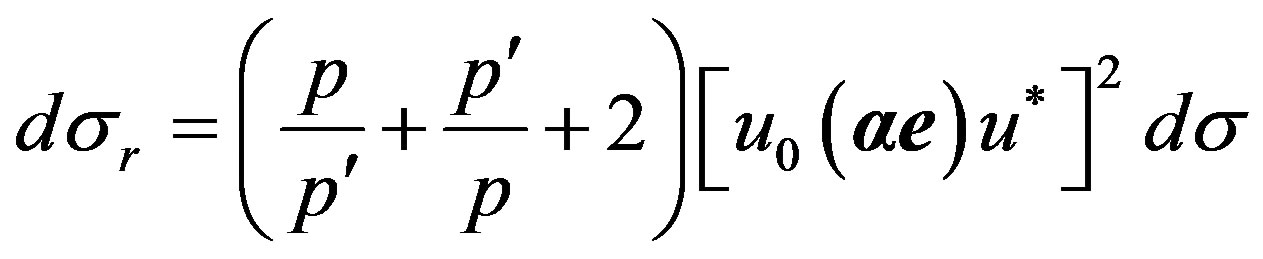 , (44)
, (44)
Taking into account 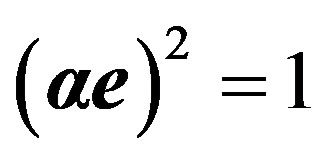 [9] and
[9] and
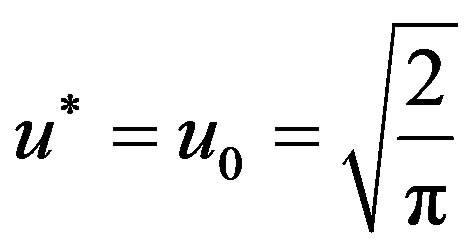 at
at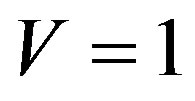 , see the formula (5), we have:
, see the formula (5), we have:
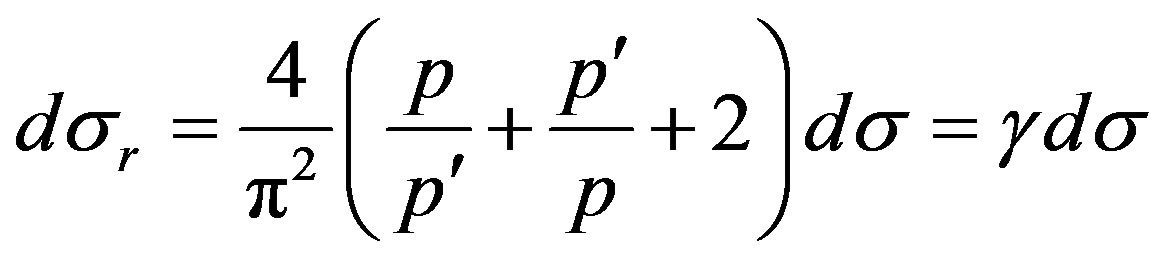 , (45)
, (45)
Hence, for the account of ultrarelativistic effects, it is necessary to multiply the differential effective section of process in not relativistic variant on value
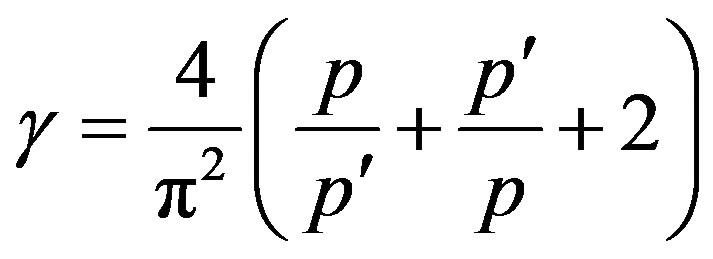 .
.
On Figure 3 dependence of relative factor
 on parameter of efficiency of braking
on parameter of efficiency of braking 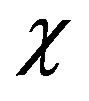 for various elements of a biotissue in an ultrarelativistic case is shown.
for various elements of a biotissue in an ultrarelativistic case is shown.
Let’s consider in more detail used conditions 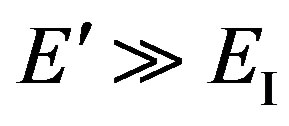 and
and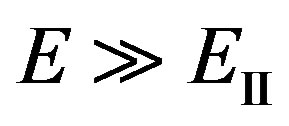 . We assume also, that the quantum concerning low energy is radiated. Hence
. We assume also, that the quantum concerning low energy is radiated. Hence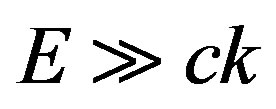 . The first condition gives:
. The first condition gives:
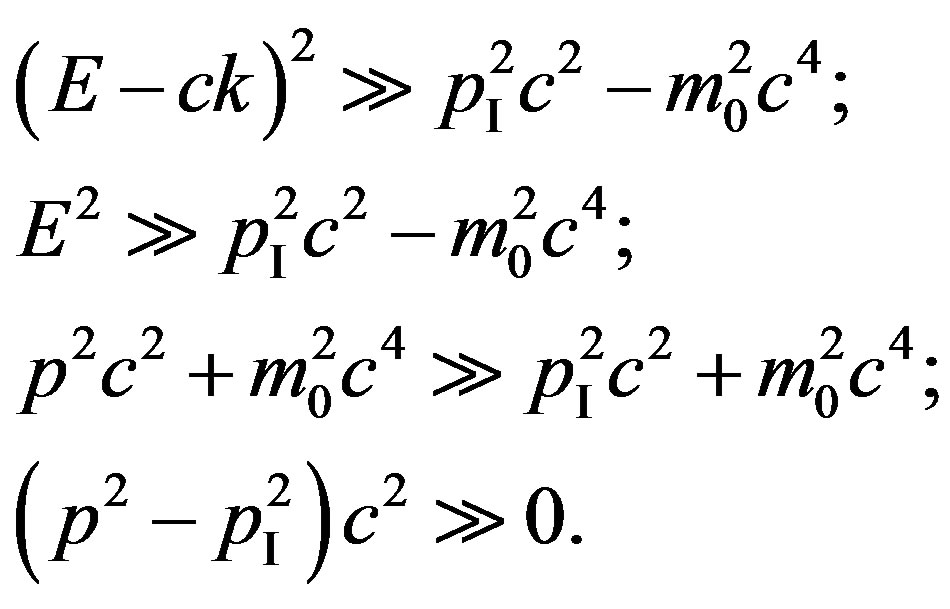
Taking into account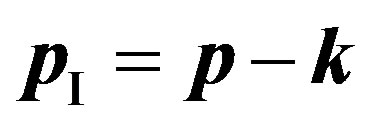 , we have
, we have 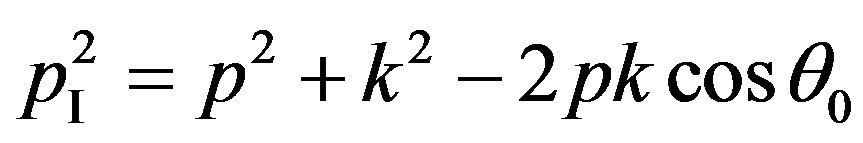 , where
, where 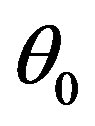 is an angle between an initial direction of the electron and radiated photon. Hence:
is an angle between an initial direction of the electron and radiated photon. Hence:
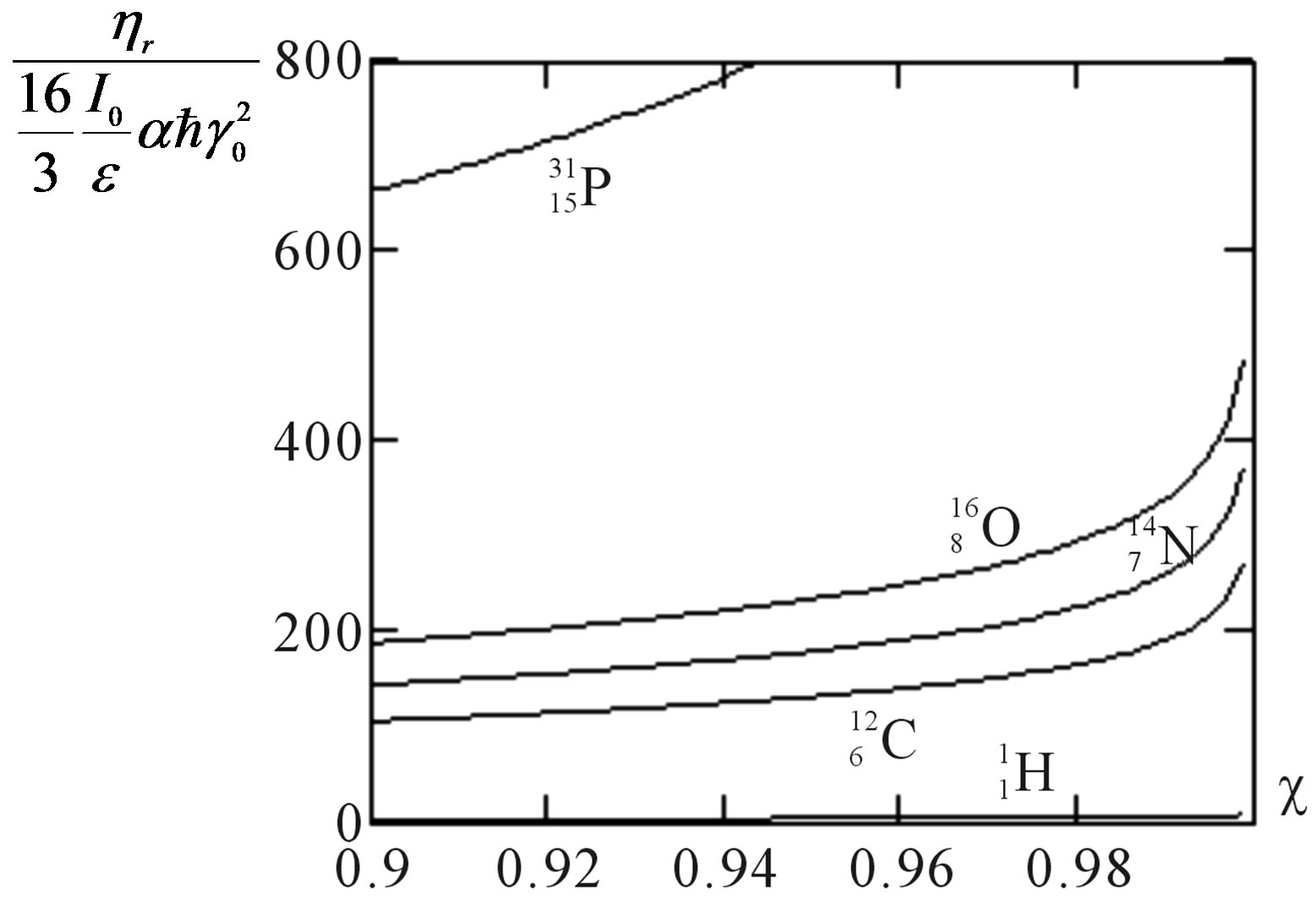
Figure 3. Calculate dependence of relative size of value ηr on parameter of efficiency of braking of β-electrons and charging number of elements of a biotissue in an ultrarelativistic case.
 (46)
(46)
The condition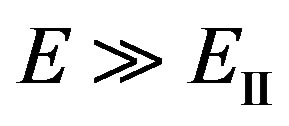 , taking into account (17), gives:
, taking into account (17), gives:
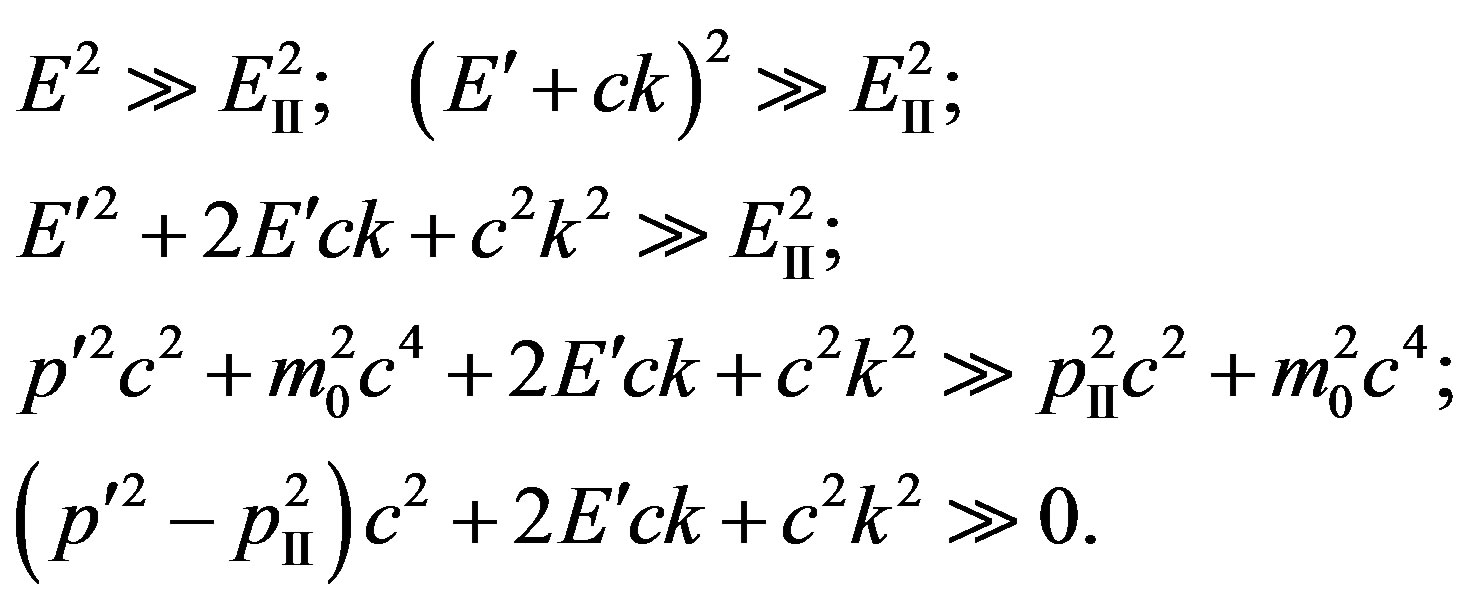
Taking into account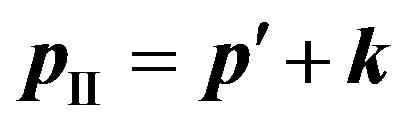 , we have
, we have  , where
, where  is an angle between a final direction of the electron and an impulse of a photon. Hence
is an angle between a final direction of the electron and an impulse of a photon. Hence
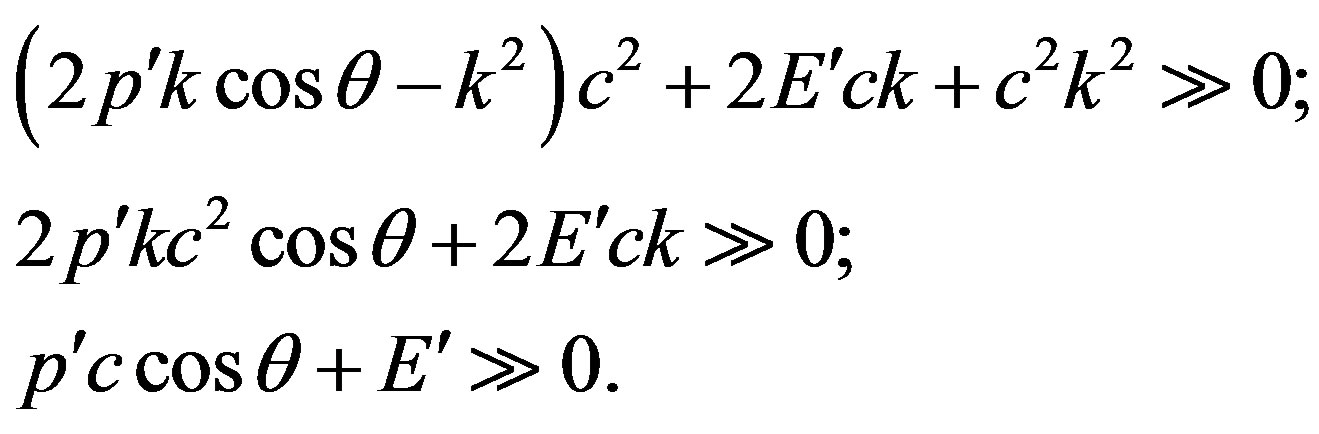 (47)
(47)
Thus, conditions  and
and 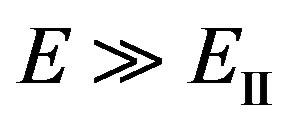 at
at 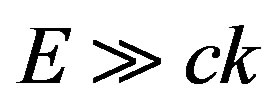 are equivalent to conditions
are equivalent to conditions 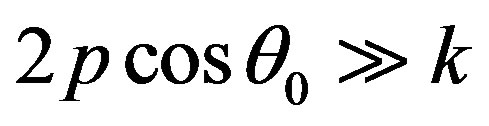 or
or
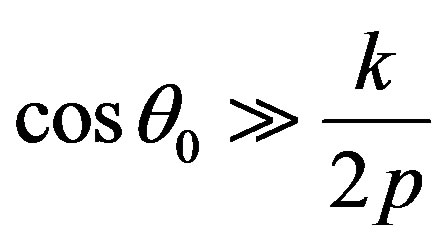 and
and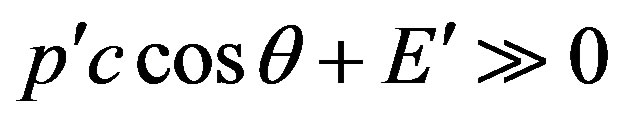 .
.
The condition 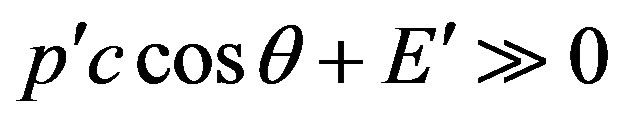 can not be discussed. The first condition specifies that, at
can not be discussed. The first condition specifies that, at  or, that too
or, that too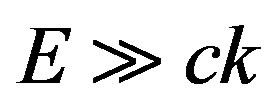 , cosine of an angle between an initial direction of the electron and a radiated photon is
, cosine of an angle between an initial direction of the electron and a radiated photon is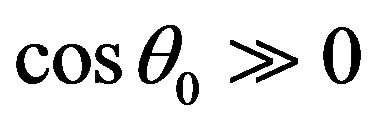 , i.e. approach to unit, and an angle
, i.e. approach to unit, and an angle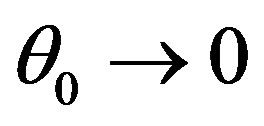 . Thus, in an ultrarelativistic variant radiation of photons is directed approximately along an initial direction of movement of the electron falling on substance that corresponds to a conclusion [9].
. Thus, in an ultrarelativistic variant radiation of photons is directed approximately along an initial direction of movement of the electron falling on substance that corresponds to a conclusion [9].
4. SPECTRUM OF THE BRAKE ELECTROMAGNETIC RADIATION
For estimation of the received results correction it is necessary to compare to known experimental data.
There is brake radiation in the X-ray range which usually received in X-ray tubes. The electrons are accelerated in space between the cathode and the anode. Between the cathode and the anode there is also accelerating voltage. At braking in substance of the anode, the electrons cause occurrence from the anode the brake electromagnetic radiation.
Comparison of the formula (16) with results of experiments [10], shows, that it does not correspond to experiments on two parameters. First, dependence of a energy flux of quantums of brake radiation on charging number Z of atoms of braking substance not square-law, but linear. Second, the frequency dependence on the contrary, it is not linear, but square-law.
According to [10] it basically it is caused according to two factors. The portion of electrons is captured by atoms into stationary orbits, and also there is a probability of return diffusion of electrons from braking substance. These phenomena were not taken into account in our analysis.
At capture of electron into a stationary orbit, it stops to participate in creation of quantums of brake radiation. Therefore the flux of energy of quantums is reduced. Effective section of electron capture by the atom proportionally to its charging number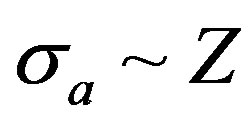 . The flux of energy of brake electromagnetic radiation is inversely proportional to effective section of electron capture
. The flux of energy of brake electromagnetic radiation is inversely proportional to effective section of electron capture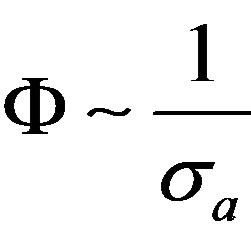 therefore linear dependence
therefore linear dependence 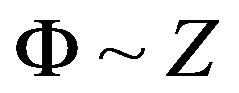 is observed.
is observed.
Intensity of return diffusion of electrons from the anode depends on their energy. Electrons with lower energy will penetrate into substance of the anode less deeply, than the electrons with higher energy. Therefore the electrons lower energy take off back from the anode is more often, and participate in creation of brake electromagnetic radiation less. It results in reduction in a spectrum of brake radiation of a fraction of low-frequency quantums. There is a nonlinear dependence of an energy flux of brake radiation on frequency of quantums.
According to results of experiments the energy flux of brake electromagnetic radiation in the X-ray tube is equal:
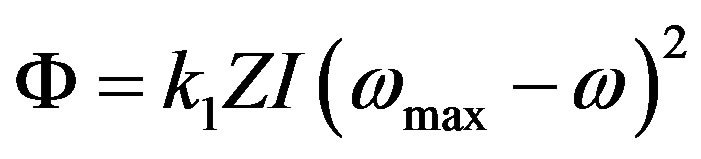 (48)
(48)
where I there is a current in the X-ray tube, determined by the electrons flux from the cathode to the anode, k1 is constant.
Carrying out simple transformations, with the account
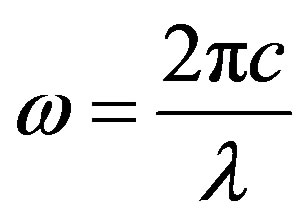 , we find dependence of spectral density of energy of brake electromagnetic radiation
, we find dependence of spectral density of energy of brake electromagnetic radiation 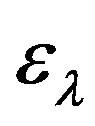 on wave length of this radiation:
on wave length of this radiation:
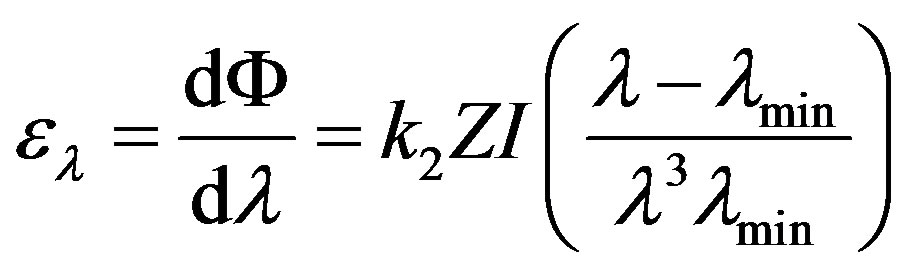 , (49)
, (49)
where  is a constant,
is a constant,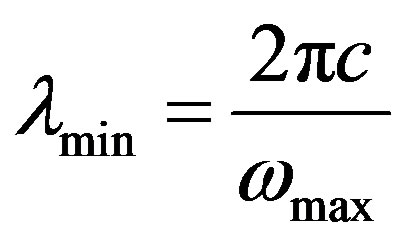 —the shortest wave length in a spectrum of brake radiation.
—the shortest wave length in a spectrum of brake radiation.
Connection of the wave length on which there is a maximum of energy of brake radiation and the shortest wave length 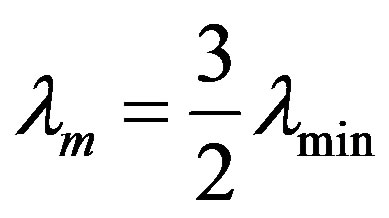 it is possible to find from the condition of function extreme of spectral density of energy
it is possible to find from the condition of function extreme of spectral density of energy .
.
On Figure 4 the approximate form of dependence of
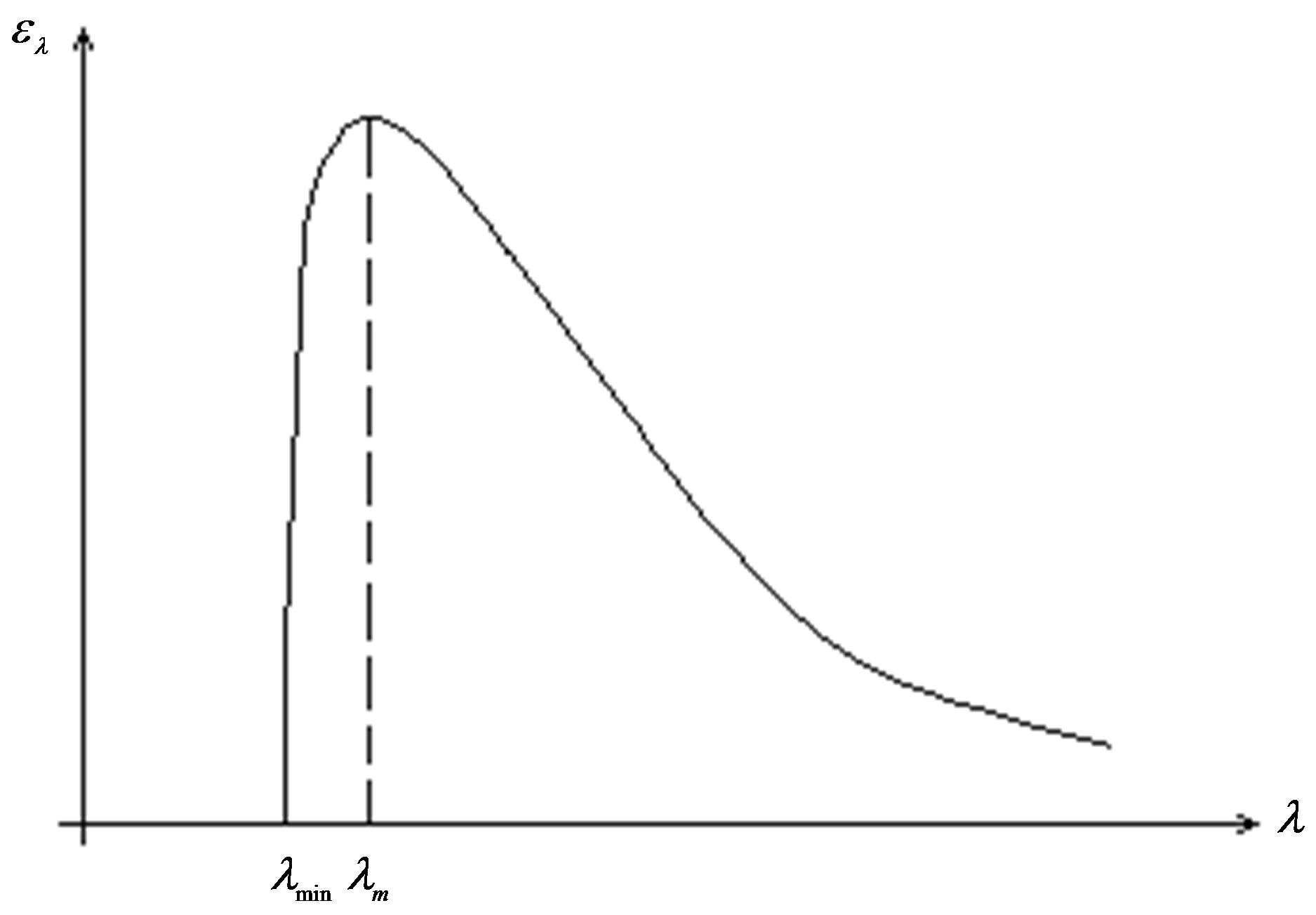
Figure 4. Form of the brake electromagnetic radiation spectrum.
spectral density of energy of brake electromagnetic radiation from wave length is shown according to the formula (49).
5. CONCLUSIONS
At braking electrons of β-rays in a biotissue there is a brake X-ray radiation which gives the essential contribution to killing action of this kind ionizing radiations.
Equivalence of relative biological efficiency of β-rays and ionizing electromagnetic radiation, apparently, is connected by that a major factor of influence on a tissue of an organism at their irradiation of β-rays is brake ionizing electromagnetic radiation.
At the analysis of influence of β-rays on a biotissue, it is necessary to take into account, that arising brake ionizing electromagnetic radiation act on rather big distance from a trajectory of movement of the electron and destroying an effect can have on all structures of a cell through which there passes the electron: DNA, membranes, etc.
For electrons relatively small energy brake radiation is directed perpendicularly planes of a scattering of electrons, and for electrons big energy brake radiation is directed approximately along a direction of electrons falling on substance.
REFERENCES
- Vasiliev, V.N., Kokontsev, A.A., Tyurnina, S.P. and Sotnikov, V.M. (2011) Wide-field skin irradiation by electrons. Medical Physics, 52, 11-19.
- Savinsky, A.K. (1984) Interaction of electrons with tissueequivalent environments. Energy Atom Izdat, Moscow.
- State Standard (1987) The state pharmacopoeia of the USSR. 11 Edition, Release 1. Medicine, Moscow, 76.
- Kudryashov, J.B. (2004) Radiating biophysics. Fizmatlit, Moscow.
- Levich, V.G., Vdovin, J.A. and Mjamlin, V.A. (1962) Course of theoretical physics. Fizmatgiz, Moscow.
- Landay, L.D. (2004) Quantum mechanic. Fizmatlit, Moscow.
- Levich, V.G. (1962) Course of theoretical physics. Fizmatgiz, Moscow.
- Berestetsky, V.B., Lifshits E.M. and Pitaevsky, L.P. (1989) Quantum electrodynamics. Science, Moscow.
- Gajtler, V. (1956) Quantum theory of radiation, Foreign Literature, Moscow.
- Blohin, M.A. (1957) Physics of X-rays. Gostehizdat, Moscow.
- Javorskij, B.M. and Detlaf, A.A. (1990) Director on physics. Science, Moscow.

