Engineering
Vol.09 No.02(2017), Article ID:74101,31 pages
10.4236/eng.2017.92004
Health Monitoring Based on Dynamic Flexibility Matrix: Theoretical Models versus In-Situ Tests
Sebastian Schommer1*, Jean Mahowald1, Viet Ha Nguyen1, Danièle Waldmann1, Stefan Maas1, Arno Zürbes2, Guido De Roeck3
1Université du Luxembourg, Faculté des Sciences, de la Technologie et de la Communication, Research Unit Engineering Sciences, Luxembourg, Luxembourg
2Technische Hochschule Bingen, Fachbereich 2-Technik, Informatik und Wirtschaft, Bingen, Germany
3Department of Civil Engineering, Division of Structural Mechanics, KU Leuven, Leuven, Belgium

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 14, 2016; Accepted: February 11, 2017; Published: February 14, 2017
ABSTRACT
The paper focuses on damage detection of civil engineering structures and especially on concrete bridges. A method for structural health monitoring based on vibrational measurements is presented and discussed. Experimentally identified modal parameters (eigenfrequencies, mode shapes and modal masses) of bridge structures are used to calculate the inverse stiffness matrix, the so-called flexibility matrix. By monitoring of the stiffness matrix, damage can easily be detected, quantified and localized by tracking changes of its individual elements. However, based on dynamic field measurements, the acquisition of the flexibility matrix instead of the stiffness matrix is often the only choice and hence more relevant for practice. But the flexibility-based quantification and localisation of damage are often possible but more difficult, as it depends on the type of support and the location of the damage. These issues are discussed and synthetized, that is an originality of this paper and is believed useful for engineers in the damage detection of different bridge structures. First the theoretical background is briefly repeated prior to the illustration of the differences between stiffness and flexibility matrix on analytical and numerical examples. Then the flexibility-based detection is demonstrated on two true bridges with real-time measurement data and the results are promising.
Keywords:
Flexibility, Damage Detection, Bridge, Modal Identification

1. Introduction
Nowadays the traffic is permanently increasing and many bridges are operating beyond their initially planned lifetime. A high number of reinforced concrete bridges were built after the Second World War and are suffering from ageing and today’s traffic load. But their safety must be guaranteed and efficient methods for structural health monitoring and damage detection are urgently needed.
Traditional visual inspections are cost intensive but not always sufficient, because they investigate only the surface. Small cracks for instance covered by coating, as well as corroded internal tendons or reinforcement may remain undiscovered.
Dynamic testing can provide an alternative or addendum for damage detec- tion, where the structure is either excited by a measured input or by unmeasured ambient forces such as wind or traffic. The modal parameters can then be identi- fied and changes of eigenfrequencies, mode shapes, damping ratios and modal masses may be caused by damage that reduces before all the stiffness and its dis- tribution.
Based on identified modal parameters, transfer functions can be computed, which describe the relationship between input (normally forces) and output (often accelerations) signals of a system [1] [2] . For N measured Degrees Of Freedom (DOFs), a N × N symmetric transfer matrix [G] can be established where any element Gpq is the transfer function between a force at DOF p and a system answer at DOF q. If the frequency of the input force is tending towards zero, it is equivalent to static loading and the transfer function [G] becomes equal to the inverse stiffness matrix, the so-called flexibility matrix. Theoretically this latter allows calculating the stiffness matrix just by inversion. However, this inversion is only feasible, if the quality of the measurements is good and the flexibility matrix is calculated based on a complete set of N identified modes. But in most practical cases of real bridges, the number of clearly identifiable modes is typically much lower than the number of measured DOFs. A decrease of the number of DOFs to the number of observable modes typically leads to an insufficient spatial resolution of the stiffness matrix.
Over the last years, several sophisticated approaches were investigated for damage assessment based on flexibility that can be found in literature.
In Yan and Golinval (2005) [3] , flexibility matrices were calculated based on modal parameters identified by a subspace identification technique. Damage can be localized from the comparison of these matrices between a damaged and a reference state. The relevance and the limitations of the technique were illu- strated by the numerical models of a cantilever beam and a three span bridge as well as experiments in laboratory conditions with an aircraft mock-up.
Duan et al. (2005) [4] used arbitrary scaled mode shapes from output-only measurements to estimate a “proportional flexibility matrix” (PFM), which has to be multiplied with a undetermined scalar factor in order to obtain the real flexibility matrix. The PFM was integrated in the Damage Locating Vectors (DLV) method developed by Bernal (2002) [5] . In a subsequent publication [6] , Duan et al. (2007) detected damage at a simulated planar truss structure, where only 23 out of simulated 53 DOFs were used to calculate the PFM.
In a model updating approach, Perera et al. (2007) [7] compared experimental and analytical flexibility matrices based on the modal assurance criterion (MAC) correlated the diagonals of the flexibility matrices built from modal parameters. The approach was initially validated by simulated scenarios, then by experimental tests within an aluminum beam of 6m length.
A multi-criteria approach for damage assessment of beam and plate structures was proposed in Shih et al. (2009) [8] . In addition to the flexibility matrix, it also includes changes in eigenfrequencies and a modal strain energy based damage index. Also based on flexibility and strain energy calculations, a method for damage identification was introduced in Nobahari and Seyedpoor (2013) [9] . One year later, Montazer and Seyedpoor (2014) [10] proposed a damage indicator called “Strain Change Based on Flexibility Index” (SCBFI). As the name implies, this index is based on strain changes in structural elements. Nodal displacements necessary to obtain the strain are separately calculated by using the flexibility matrix derived from modal analysis data. In both publications, the reliability of the proposed damage indicator was still and all tested by numerical results, where by measurement noise is simulated by perturbing mode shapes with a random error.
Reynders and De Roeck (2010) [11] offered a so-called local flexibility method detecting local stiffness variations based on measured modal parameters. This approach for damage assessment was validated by some simulated examples; a reinforced concrete beam of 6 m length in laboratory as well as in-situ tests at the Z24 Bridge in Switzerland.
Another variation of flexibility matrix was proposed by Yan et al. (2010) [12] for beam structures. The components of the so-called Angle-between-String- and-Horizon (ASH) flexibility matrix are associated to elements instead of DOFs. Indicators based on the ASH matrix were considered capable of identifying damaged elements without being affected by boundary conditions as opposed to damage indicators based on the “conventional” flexibility matrix. Additionally, it is shown by numerical examples and experimental laboratory tests that the ASH matrix allows the identification and the assessment of multiple location damage.
Weng et al. (2013) [13] adopted a substructuring method for damage asse- ssment in large-scale structures, where local damage has usually only small impact on global modal features. The flexibility matrices of the substructures were decomposed into local eigenparameters, which are more sensitive to local than global damage. The method is tested with a FE-model of the Guangzhou New TV Tower.
Furthermore, Chen et al. (2014) [14] presented a mathematical approach to derive the flexibility matrix from a singular stiffness matrix of typical free-free system (without support) and vice versa. Based on modal flexibility matrix and without a Finite-Element (FE) model, Sung et al. (2014) [15] dealt with damage detection of cantilever beam-type structures such as high-rise buildings. The methods were validated by numerical simulations as well as down-scaled models in the laboratory.
Masoumi et al. (2015) [16] calculated the generalized flexibility matrix as proposed by Li et al. (2010) [17] for a FE model of a 2D-frame structure and another model of a Howe-truss. Cracks were modelled by stiffness reductions using an equation defined by Perera et al. (2009) [18] . Then, the inverse problem of damage identification was solved by using the “Imperialist Competitive Algorithm” (ICA) as described by Atashpaz-Gargari et al. (2007) [19] .
Stutz et al. (2015) [20] identified damage by a model updating process based on flexibility matrices. The used objective function was defined by the difference between an experimentally measured flexibility matrix and the corresponding one predicted by the FE model using the Frobenius norm. As parameters dimensionless nodal cohesion factors were used. The influence of the damage location and of noise in the measured data was investigated for a simply supported Euler-Bernoulli beam. Different stochastic optimisation methods were compared.
Along these lines, it is shown that flexibility-based methods are mostly validated by numerical models or laboratory tests. Far more seldom a paper dealing with in-situ tests at real bridge structures can be found. The obvious reasons may be the high costs and logistic effort for such tests as well as the fact, that a still used structure cannot be artificially damaged for test purposes. On the other hand, a real structure has to be monitored over several years or even decades in order to see effects of accumulating damage. Only the demolishing of a structure may offer the opportunity for extensive tests. But for the sake of transfer from academic researches to practical application, such real-life tests are indispensable. Therefore, a relevant contribution of this paper is the performance of in-situ tests and the analysis based on flexibility for two bridges in Luxembourg.
The present paper discusses practical possibilities and limitations of damage localisation based on the flexibility matrix. The necessary theoretical background is repeated and it is shown that an inversion of flexibility matrix to obtain the stiffness matrix with sufficient resolution is often impossible in practice, as the number of observable measured modes is limited. However, from vibrational measurement, the monitoring of identified flexibility matrices may be useful for damage detection. The efficiency depends on several factors, namely the bearing conditions and the influence of environmental temperature.
After some numerical examples, two real bridges are examined in the following. The first bridge is a new real structure without damage that the influence of temperature on stiffness is very important. The second real structure is a pre- stressed concrete bridge. Increasing artificial damage in multiple steps is identified and localized correctly by the changes in the flexibility matrix.
2. Theoretical Background
Cracking of concrete leads to reduction of local rigidity or stiffness. Hence, iden- tification and localisation of stiffness changes compared to the healthy reference state is therefore a logic strategy for damage detection. Structural health moni- toring may therefore be done by permanent monitoring or by repeated tests at distinct time intervals.
Static loading tests with the analysis of deflection line show a long tradition in civil engineering. However, these tests may become cumbersome, as a bridge should be loaded for at least a few hours by known mass until a steady state is reached. During this time, the traffic must be stopped that is inconvenient and may generate considerable costs. Additionally, heavy load testing (going beyond the service loading) may increase already present damage. Therefore, alternatives or amendments are welcome, e.g. dynamic tests either by permanently or periodically installed monitoring systems.
The discretisation of a continuum, e.g. by the finite element method, including N degrees of freedom (DOF), leads to the following differential equation of motion.
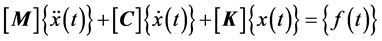 (3-1)
(3-1)
where [M], [C] and [K] is respectively the mass-, damping- and stiffness-matrix.
The Frequency Response Function (FRF) matrix  of the dimension N × N can be deduced from this differential equation.
of the dimension N × N can be deduced from this differential equation.
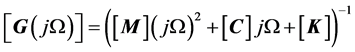 (3-2)
(3-2)
It is obvious that for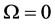 , i.e. for a constant excitation force, the FRF matrix is equal to the inverse stiffness matrix
, i.e. for a constant excitation force, the FRF matrix is equal to the inverse stiffness matrix 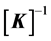 of the structure. If the stiffness matrix and its changes are known, it is straightforward to localize damage by simply looking for elements of reduced stiffness.
of the structure. If the stiffness matrix and its changes are known, it is straightforward to localize damage by simply looking for elements of reduced stiffness.
The partial fraction decomposition of this transfer function matrix can be formulated as follows (cf. [1] [2] ).
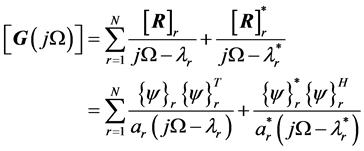 (3-3)
(3-3)
where index r refers to an individual mode.
The last equation reveals that the FRF matrix can be represented by the ensemble of eigenvalues 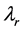 and corresponding mode shapes vectors
and corresponding mode shapes vectors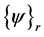 . The mode shape
. The mode shape 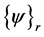 dyadic product is scaled by factor ar, which is called Modal A. It can be obtained from the state space formulation of the system as described by Wang et al. (2011) [21] .
dyadic product is scaled by factor ar, which is called Modal A. It can be obtained from the state space formulation of the system as described by Wang et al. (2011) [21] .
By evaluating Equations (3-2) and (3-3) for the case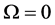 , the inverse stiff- ness matrix can be calculated based on experimentally identified modal parame- ters, including the scaling factor Modal A. This inverse stiffness matrix is often called flexibility matrix
, the inverse stiff- ness matrix can be calculated based on experimentally identified modal parame- ters, including the scaling factor Modal A. This inverse stiffness matrix is often called flexibility matrix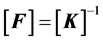 .
.
For the special case of proportional damping, i.e. 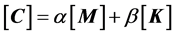 with
with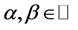 , Equation (3-3) can further be simplified (cf. [1] ):
, Equation (3-3) can further be simplified (cf. [1] ):
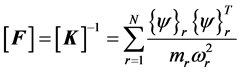 (3-4)
(3-4)
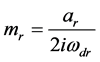 (3-5)
(3-5)
The quantity 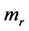 is the so-called modal mass [kg] and
is the so-called modal mass [kg] and  is the angular eigenfrequency according to mode r of the damped system. By normalization the mode-shapes to Unit Modal Mass (UMM) mr = 1, this factor is implicitly con- tained in the UMM-normalized modes-shapes.
is the angular eigenfrequency according to mode r of the damped system. By normalization the mode-shapes to Unit Modal Mass (UMM) mr = 1, this factor is implicitly con- tained in the UMM-normalized modes-shapes.
For low damped systems as for instance bridges, it is common to assume proportional damping and to use this simplified formula for the calculation of the flexibility matrix.
Theoretically, the stiffness matrix can hence be calculated by just inverting the flexibility matrix. But if the modal parameters were identified experimentally, the number of well identified modes M is often smaller than the number of measured DOFs N, as higher modes are more difficult to excite and to measure with precision. Hence, the sum in Equation (3-3) is truncated after r = M ≤ N. Due to the square of angular eigenfrequency in the denominator, the contribution of higher modes to the flexibility is quite small compared to lower modes. Therefore, adequate results for [F] may be obtained even with M < N.
Since the flexibility matrix is calculated from the dyadic products of M mode shape vectors, a N × N flexibility matrix has the rank M. If M < N, the resulting flexibility matrix cannot be inverted, meaning that the stiffness matrix cannot be calculated using this approach. Nevertheless, the identified flexibility matrices can still be useful for damage localisation for typical bridge structures. It is shown in the following by several numerical and analytical examples as well as in-situ measurements on two real bridges.
3. Theoretical Models
In this section, three theoretical examples with different damage locations are analysed to discuss the usability of the flexibility matrix for damage detection and localisation. It involves a simply supported concrete beam, a cantilever beam and finally a continuous beam. The beam models are simulated in ANSYS and consist of BEAM3 elements (2 translational and 1 rotational DOFs). The following material properties and geometry were used:
・ Young’s modulus: 3 × 1010 N/m2;
・ Poisson’s ratio: 0.18;
・ Density: 2300 kg/m3;
・ Cross section: 0.3 × 0.3 m2;
・ Length: 4 m.
3.1. Simply Supported Beam
The beam model consists of 20 BEAM3 elements with N = 63 DOFs in total [22] . As the occurrence of cracks reduces in fact the bending stiffness EI, damage can be simulated by varying Young’s modulus E and moment of inertia I.
Different damage scenarios are simulated by reducing the bending stiffness EI by 5% and 30% respectively. The damage is provoked in the middle (elements 10 and 11) and in an eccentric location (elements 4 and 5) as indicated in Figure 1. The name of the respective damage state is referred as follows: M5% indicates a damage in the middle of the beam with the reduction of EI by 5%. Furthermore, E5% represents an eccentric damage with the same stiffness reduction.
For every damage state, the flexibility matrix was calculated according to Equations (3-4) with the mode shapes simulated in ANSYS and normalized to Unit Modal Mass (UMM). Like mentioned above the model contained 63 DOFs in total, where 3 are constrained due to the supports. Hence a set of 60 modes was considered for the 60 × 60 flexibility matrix. Figure 2 shows the part of the matrix for the DOFs of vertical displacement(y), whereupon DOFs 1 and 21 were constrained.
A diagonal element of the flexibility matrix can be interpreted as the deformation at the DOF where a single unit force (1N) is applied. The diagonal elements are shown in Figure 3(b).
Additionally, the contributions of the first 10 bending modes in the flexibility matrix are plotted as dashed lines. It is obvious that the first two bending modes have predominant influence on the flexibility and that the influence of B2 is already much smaller than the one of B1. As the contribution to the flexibility from the third mode seems insignificant, it seems even possible to attain a good approximation for the flexibility matrix, if the sum in Equations (3-4) is truncated after r = 2. This is important, because in the experimental modal analysis it is impossible to excite and measure accurately all modes as will be shown in sec- tion 0.
The approach to use only lower modes for the flexibility matrix calculation is convenient for the experimental procedure in practice. The diagonals of the flexibility matrices based on the first 2 bending modes are presented in Figure 3(b) for all the damage states. The zones of damages (eccentric as E5% and
Figure 1. Different damage states.


Figure 2. Flexibility matrix of the healthy state [22] : (a) Surface plot [F] for intact state; (b) Contour plot [F] for intact state.
E30% as well as in the middle as M5% and M30%) are also highlighted in Figure 3(b). By comparing the curves for M30% and E30%, it can be seen that damages in the middle of the beam (M5% and M30%) have higher influence on the flexibility matrix than eccentric damage (E5% and E30%).
The difference between the flexibility matrices of a damage state and the intact state is presented in Equation (4-1) [23] where d represents a current state under investigation and u the undamaged or intact state.



Figure 3. Diagonal elements of the flexibility matrix. (a) Modal decomposition for the intact state; (b) Intact and all damage states.
These differences are shown in Figure 4, where all diagrams were scaled to the same maximum. As already mentioned above, the central damage is easier to detect because it presents larger influence than the eccentric. However due to the eccentric damage E30%, Figure 4(d) shows that the most important change in flexibility does not occur in the most flexible part of the beam―usually in the middle, but close to the actual location of the damage. It proves in this case of


Figure 4. Flexibility changes compared to the undamaged state, presented in the same scaling [22] : (a) M5%-intact; (b) M30%- intact; (c) E5%-intact; (d) E30%-intact.
simply supported beam, it is possible not only to detect the presence of damage, but also to localize it based on the flexibility evaluation.
In order to improve the visualisation of changes especially due to small dam- ages, a relative calculation of the differences between the flexibility matrices can be useful. Following row number i and column number j in the flexibility matrices, the relative difference is defined as:

Figure 5 shows the absolute as well as the relative changes in diagonal elements of the flexibility matrices for different damage states compared to the intact state. As expected, for the centric damages the position of maximum changes coincides well with the damage position. For the eccentric damages the maximum changes occur very near to the damaged location.

Figure 5. Absolute and relative differences of the diagonal elements of the flexibility matrices [F]: (a) Absolute differences; (b) Relative differences.
3.2. Cantilever Beam
3.2.1. Cantilever Beam-Analytical Solution
Considering in Figure 6 the cantilever beam with a total length L, subdivided into three parts and denominated by indexes 1, 2 and 3 respectively [22] . The initial beam has a constant cross section with moment of inertia I1. Damage is introduced in section 2 with length b by reducing the moment of inertia to I2.
For each section the deflection w(x) is calculated analytically by integration of the following equation:

Taking into account the boundary conditions, the bending line of the three sections is formulated:

Figure 6. Model of the cantilever beam for the analytical survey.
At a discrete location x the flexibility can be determined for a chosen set of a and b:

In the following, the same material and cross section properties as for the
simple beam in the first example are used. By choosing






Figure 7 shows the results for n equal to 0, 2, 4, 6 and 8. Each graph is repre- sented with two vertical ordinates. The left ordinate in blue outlines the flexibi- lity

Figure 7 shows that damage occurring close to the clamped end can be detected and localized by the peak of the relative difference of the flexibility. But if damage moves toward the free end, it can no longer be localized by this local maximum. The closer damage is located to the free end of the beam the lower is its influence on the flexibility. For n > 3, the highest relative change is detected at the free end. But also in these cases localisation is still feasible by simple identi- fication of the starting point of the relative change.
3.2.2. Cantilever Beam―Flexibility Matrix Calculated from Mode Shapes
Alternatively, a finite element model of 20 BEAM3 elements, with the same properties as for the simple supported beam, is examined as for the cantilever beam but here by using ANSYS. The flexibility matrix is calculated based on UMM normalized mode shapes in accordance with Equation (3-4).
Two damage scenarios are investigated again by a 30% reduction of Young’s modulus: first, near the fixed support named B30% and second, near the free end named E30% as presented in Figure 8.
Figure 9(a) shows the contribution of the first 10 pure bending modes to the flexibility, while the sum adds up to 60 modes and is presented by the blue



Figure 7. Analytical examination on the flexibility of the cantilever beam with different damage positions: (a) Damage section 0 to 1; (b) Damage section 2 to 3; (c) Damage section 4 to 5; (d) Damage section 6 to 7; (e) Damage section 8 to 9.
Figure 8. Sketch of the cantilever beam with the two damage states, marked in colour at the beam elements 5 to 6 (green) and 17 to 18 (red).

Figure 9. Diagonal elements of the flexibility matrix according to the modal decomposition for the intact (a) and all damage states (b) for the cantilever beam: (a) Modal decomposition for the intact state; (b) Intact and damage states.
continuous line. Again it is obvious that the contribution of the first bending mode to the flexibility matrix is by far predominant and higher modes have no visual effect and so are more or less negligible. Therefore, only the first two modes are taken into account for flexibility calculation. Figure 9(b) highlights that there are only very small changes due to the damage; the E30% case coincides visually with the curve of the intact state. The diagonal values in Figure 9(b) show a very good correlation regarding the shape and the magnitude compared to the analytical results in Figure 7(b).
The absolute and the relative differences of the diagonal elements of the flexi- bility matrix are shown in Figure 10(a) and Figure 10(b). The relative differ- ence in the case B30% in Figure 10(b) can directly be compared with the green continuous line in Figure 7(b). Both curves show a high similitude with a maximum variation of 7% - 8%. And in case the damage is closer to the free end of the beam (E30%), the relative differences are both about 0.3% at the free end of the beam in Figure 7(e) as well as Figure 10(b). Furthermore in Figure 10(b),
we see in the relative differences a deviation if we include all modes or only two bending modes.
3.3. Continuous Beam
The last theoretical case is investigated for a continuous beam as sketched in Figure 11. Different damage scenarios are marked by different colours and are examined. The damage states are indicated according to the element number. In all cases a 30% reduced elastic modulus is assumed.

Figure 10. Differences of the diagonal elements of the flexibility matrices [F] for the cantilever beam: (a) Absolute differences; (b) Relative differences.
Figure 11. Continuous beam with different damage states.
3.3.1. Damage Assessment Based on Flexibility
In Figure 12(a) it is shown that the first bending mode B1 is again predomi- nantin its contribution to the flexibility matrix. Hence only the first two modes were considered.
Figure 12(b) displays diagonal elements of the flexibility matrices in every state and it indicates the respective locations of damage by vertical dashed col- umns. The absolute and relative differences are compared to the intact state and are presented in Figure 13. Due to the constrained DOFs at the supports the flexibility around the supports tends towards zero. In order to avoid division by zero the values of the relative differences on the supports are not calculated and not shown.
From the two graphs in Figure 13 four types of damage can be distinguished:
・ Damage within the smaller span (EL4): The absolute difference shows a dominant peak at element 4 and another second peak in the middle of the long span (elements 14 - 15). This second peak is considerably lower in the relative difference in Figure 13(b). Hence localisation of damage in element 4 is possible.
・ Damage on the intermediate support (EL8): The absolute difference in Figure 13(a) shows an important peak in the middle of the long span. However, the relative difference in Figure 13bdoes not show a real peak, but reveals two zones with high values in the middle of the long span and close to the end support of the short span, which results from errors due to the division of small absolute values. So damage localisation by peak in this case is not possible, but only the qualitative information that something happened.
・ Damage within the long span (EL11, EL15, EL18): The absolute difference points out accurately the locations of damages. The relative difference shows again false side lobes, especially for (EL11), (EL18).

Figure 12. Diagonal elements of the flexibility matrix for the continuous beam system: (a) Modal decomposition for the intact state; (b) Intact and damage states.

Figure 13. Differences of the diagonal elements of the flexibility matrices for all the damage states compared to the intact state of the continuous beam: (a) Absolute differences; (b) Relative differences.
・ Damage on end supports (EL1, EL20): The absolute difference increases near the end supports, while the relative difference reaches a maximum at node 2 and 20 respectively. Between nodes 8 to 16 there is no visible difference. Therefore, good damage detection is not really feasible taking into account the noise on real measurements.
Summarily, it is stated that the relative difference works well, but may lead to inaccurate interpretations when damage occurs close to the supports.
3.3.2. Damage Assessment Based on Stiffness
In the following the flexibility based results according to Equation (3-4) are compared to the detection based on the stiffness matrix, provided the latter is known from an FE-model. The absolute and relative differences are calculated for the stiffness matrix for every state and are presented in Figure 14. It should be noted that the stiffness close to the supports are set to 0, as the FE-model does not include their entries. Consequently, the relative changes in flexibility on the supports were also not shown.
Of course the stiffness matrix allows a straightforward damage localisation, even for damage close to the intermediate support (EL8).
3.3.3. Discussion
The above illustrations show that damage detection based on the flexibility is feasible, though the localisation may become difficult close to the supports due to the small absolute values. But the presence of damage is still detectable by an increase of flexibility.
For a cantilever beam damage can be localized by the shape of the flexibility variation: the absolute difference starts to deviate from zero at the location of damage then increases monotonously toward the free end. On the other hand, the relative difference shows a peak close to the damage location, if it is close to

Figure 14. Differences of the diagonal elements of the stiffness matrices [K] for the continuous beam, calculated in ANSYS: (a) Absolute differences; (b) Relative differences.
the clamped end. If damage is close to the free end the flexibility curve leaves the zero line at the damaged location and increase towards the free end.
The stiffness matrix would be better in any case; but this is practically not possible by inversion of the experimentally determined dynamic flexibility matrix as explained in section 2.
4. Experimental Tests
In this section, several in-situ tests on real roadway bridges are presented. The reliability and feasibility of flexibility for damage detection is discussed. Furthermore, the influence of environmental effects, namely temperature changes, is also considered.
4.1. The “Useldange” Bridge
It is a small roadway bridge crossing a creek in Useldange, a town in Luxem- bourg. This new bridge is monitored for several years with multiple sensors. Though there was no damage in the test period, considerable differences of measured modal parameters and the deduced flexibility matrices are observed between summer and winter.
Figure 15 shows a photo of the bridge and Figure 16 explains the experimen- tal setup for the forced excitation tests. Only two transducers were installed on the East side to separate bending and torsional modes, which were not included in the damage analysis.
In total six measurements were done, whereof three in summer (August 2012) and three in winter (February 2013). The bridge was always excited with an unbalanced mass exciter system with a swept sine force of constant force amplitude of 2.5 kN, while the frequency was varied from 3 Hz to 10 Hz at a sweep rate of 0.02 Hz/s. The response of 21 accelerometers of type PCB393B04 was captured
Figure 15. Bridge in Useldange in spring 2015.
Figure 16. Experimental setup for the measurements of the bridge in Useldange.
at a sample rate of 2500 Hz. In order to calculate FRFs the signals were processed using a Hanning window on separated time intervals of 100 000 samples with an overlapping of 80%. With this setting a frequency resolution of 0.0125 Hz is achieved. Two measurements were done in winter (named W1 and W2) within a time interval of 20 minutes. Furthermore, measurement W3 was performed 1.5 h later. In summer, the first measurement S1 was followed by two consecutive measurements 3 hours later, referred as S2 and S3. Table 1 shows the tempera- tures of the structure and the air during these measurements. More detailed can be found in [22] .
Additionally output-only modal analysis was performed for a permanent monitoring of this bridge for several years [22] [23] . Figure 17 displays the eigenfrequencies identified for the first bending mode B1 and the first torsional mode T1, which show a high dependency on temperature. An explanation for the high sensitivity to temperature is the thick asphalt layer of 25 cm, whose
Table 1. Air and material temperatures recorded during different days (* retrieved from online data captured at the meteorological station in the Lycéeclassique de Diekirch, meteo.lcd.lu).

Figure 17. Eigenfrequencies identified in winter and summer for the bridge in Useldange [22] : (a) Bending mode B1; (b) Torsional mode T1.
elastic modulus is drastically varying with temperature [24] . Furthermore, this type of a light mixed steel-concrete construction, where two of three supports are fixed by elastomeric bearing pads is sensitive to temperature effects, as can be seen in Figure 17.
As in previously shown examples, the flexibility is calculated based on measured mode shapes and eigenfrequencies and then the diagonal elements are analysed. The modal decomposition of the flexibility matrix is illustrated in Figure 18(a) including the first bending B1 and the first torsional mode T1. They both have high influence on the flexibility matrix.
By comparing the diagonal elements of the flexibility matrices in Figure 18(b) it is visible that the variations during summer are higher than the variations in winter.
Therefore Figure 19 evaluates the relative differences between the individual measurements. Near the supports, where the absolute values of the flexibility are very small, the relative differences were not calculated in order to avoid division by very small values, which has no physical meaning. Hence, there are no values indicated at DOFs 1, 13, 14, 17 and 18.

Figure 18. Diagonal elements of the flexibility matrices for the winter and summer measurements: (a) Modal decomposition for measurement W1; (b) Ensemble of winter and summer measurements.
Figure 19. Relative differences of the diagonal elements of the flexibility matrices for the winter and summer measurements [22] .
Although there was no damage at the bridge, important variations of the measured flexibility can be observed. But the variations obtained in the same season (e.g. W2-W1, S3-S2) are quite low (maximum 10%) compared to the big differences between summer and winter measurements. All summer-winter curves show a constant parallel shift, as the asphalt temperature and hence its stiffness changed constantly over the length of the bridge. Damage would be reflected by local changes of the flexibility, so that the observed global shift is due to changed ambient conditions.
4.2. Bridge Champangshiehl
The bridge Champangshiehl [25] was built from 1965 to 1966 and connected the centre of Luxembourg with district Kirchberg (cf. Figure 20). Before its demoli- tion for reasons of changed urban planning in 2011, the bridge was used as test object and subjected to both static and dynamic tests after introduction of artifi- cial damage in multiple steps.
The prestressed concrete bridge had two spans of 65 m and 37 m as sketched in Figure 21. The superstructure of the bridge was a prestressed box girder with 32 parabolic, 24 upper straight-lined and 20 lower straight-lined subsequently injected tendons. The roadbed had a width of 12.5 m and the dimension of the box girder was 6.5 m × 2.62 m, as illustrated in Figure 22. The bridge was made of concrete B450 with measured elastic modulus of approximately 33,000 N/mm2, compressive strength of 37 N/mm2 and tensile strength of 3.6 N/mm2. Furthermore, the tendons were made of Steel ASTM A416 57T with Young’s


Figure 20. Bridge Champangshiehl: (a) Photo on 08.02.2010; (b) Photo on 25.09.2010.
Figure 21. Experimental setup for dynamic tests, as well the cross-section in the middle of the large span (at 0.5L).
Figure 22. Schematic cross-section presenting all the tendons in the Champangshiehl bridge.
modulus of 194,000 N/mm2 and tensile strength of 1730 N/mm2. They were pre- tensioned with a force of 1177 kN (σ = 1050 N/mm2). The superstructure was supported by two abutments and one intermediate column made of reinforced concrete. The West abutment at the end of the large span was equipped with a roller bearing, whereas the East abutment was fixed. In 1987, 56 external pre- stressed steel cables were added into the box girder of the large span for safety reasons.
The dynamic tests described here were done by an unbalanced mass exciter with a force amplitude of F = 2.5 kN. A swept sine force excitation with a sweep rate of 0.02 Hz/s was applied and the introduced forces were measured by force transducers of type HBM U10M with a range 12.5 kN. The response was re- corded with 20 accelerometers of type PCB 393B04 with a sample rate of 1000 Hz.
The accelerometer positions are shown in Figure 21. Two campaigns of mea- surement were performed with coarse (20 points) and dense grids (100 points) respectively. The present study considers the coarse grid only and the acceler- ometer positions are displayed by blue dots (Figure 21).
Damage was introduced by cutting tendons to create local cracking of the concrete. Different scenarios are shown in Figure 23 and Table 2. Furthermore, the cracks observed within each damage scenario are described in Table 3.
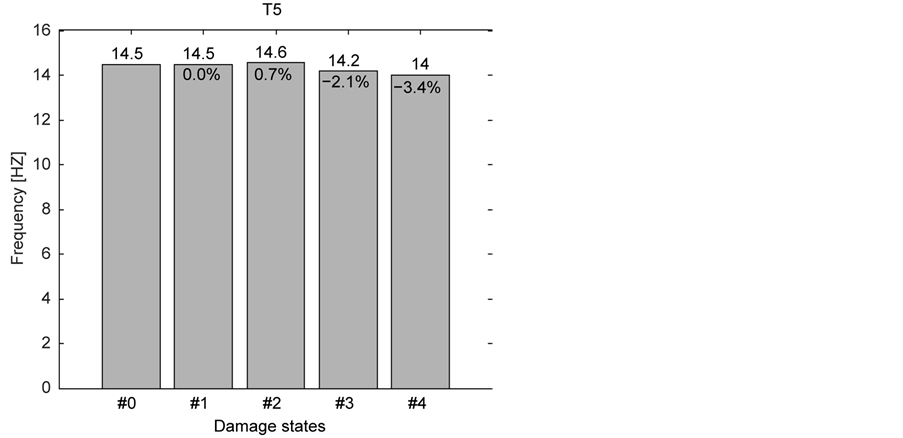
The dominating three bending and four torsional modes were identified for all damage states. The change of the eigenfrequencies is shown in Figure 24.
In the following the changes of flexibility matrix due to the increasing damage are examined. The flexibility-matrix is calculated with the above mentioned 7 modes, whose individual contributions are shown in Figure 26(a). The summed up flexibility matrix is depicted in Figure 25 as 3D and as contour plot for the 20 DOFs measured on two sides of the bridge deck. As shown in Figure 21, DOF 1 to 10 were located on the South side and DOF 11 to 20 on the North side. The bold black lines separate the two South and North sides, whereas the dashed lines pinpoint the intermediate support on the column.
Figure 23. Cross-section for damage scenarios #1 - #4.
Table 2. Description of the damage scenarios according to the cutting sections.
Table 3. Description of cracks according to the damages.
Figure 24. Eigenfrequencies of 7 modes identified for all states of the Champangshiehl bridge, excitation force of 2.5 kN by the unbalanced mass exciter [22] .

Figure 25. Flexibility matrix of the intact state for both sides of the Champangshiehl bridge: (a) 3D-view; (b) Contour plot.
It is obvious that the highest flexibility was found in the largest span, which can be clearly recognized in Figure 25.
The contribution of the first bending mode B1 is predominant in the sum, what is revealed by the modal decomposition in Figure 26(a) for the reference state without damage. The torsion mode T2 adds smaller contribution to the flexibility matrix. The influence of higher modes starting from the bending-mode B3 is clearly smaller.
The computation of the flexibility was done for all the damaged states and the diagonal elements are presented in Figure 26(b). Indeed, until damage scenario #2, no important changes in the flexibility matrix can be noticed. But for damage state #3 and #4, an increase in the middle of the large span becomes evident. The different levels of damage are detected in the correct order, especially within the large span of the bridge.
For a better comparison of the changes, the differences of flexibility matrices are presented in Figure 27 by the diagonal elements. Damage at the cutting line in the middle of the large span is very well localized. On the other hand, the damage directly on the intermediate support (damage scenario #2 and #4 on the DOFs 7 and 17 respectively) are not revealed; they only lead to an important difference of flexibility in the middle of both spans.

Figure 26. Diagonal elements of the flexibility matrices for all the damage states of the Champangshiehl bridge: (a) Modal decomposition in the intact state; (b) All damage states.

Figure 27. Differences between diagonal elements of the flexibility matrices for all the damage states compared to the intact state of the Champangshiehl bridge: (a) Absolute differences; (b) Relative differences.
5. Conclusions
Cracks inside concrete lead to a stiffness reduction in structure. Therefore, damage may be detected and even localized by identifying local reduction of the stiffness matrix or by a local increase of the flexibility.
The stiffness matrix itself would naturally be more efficient for damage local- isation. But an inversion of the flexibility matrix deduced from experimental vi- brational measurements is often impossible. It is usually rank deficient, because the number of identifiable physical modes is in most practical applications lower than the number of measured DOFs. In the last example of the Champangshiehl bridge, totally 7 modes could be clearly identified from the measurements of 20 sensors. But 7 sensor-positions for a bridge of approximately 100 m length does not lead to reasonable resolution in space.
Nevertheless, damage detection based on the flexibility matrix is feasible and its informative value depends on the position of damage relative to the supports. One originality of the paper is that it synthetizes diverse revelations of flexibility change identified from practical measurements. The revelation depends on type of bridge structure (cantilever, continuous beam...) and location of damage (among 2 supports, toward a free end...). Since the behaviour of the flexibility change relates to these conditions, such a synthesis is believed useful for engineers in the damage detection of different bridge structures.
As examined in section 5.1, flexibility measurements of the undamaged bridge in Useldange show important differences between summer and winter, though there is no damage. In summer, the eigenfrequencies of the bridge are much lower than in winter and hence the calculated flexibility is much higher. Additionally, the scatter of the results in summer is higher than in winter, which can be explained by the local temperature variation due to local solar irradiation. As the eigenfrequencies of this bridge depend strongly on temperature, a compensation is necessary prior to the extraction of modal parameters and hence prior to the calculation of the flexibility matrix for condition monitoring. A very simple compensation would be to measure only on cloudy days without solar irradiation in order to keep the temperature constant along the bridge and close to the reference measurements.
For the Champangshiehl Bridge with severe artificial damages, the results are similar to the continuous beam analysed in section 4.3. The first cutting line was located in the middle of the large span and hence well identified with the absolute and the relative differences of flexibility. But the second cutting line above the intermediate pylon was not detected due to the low absolute flexibility or the high stiffness.
The theoretical examples as well as the in-situ tests presented in this paper show that it is possible to detect or even localize damage by interpreting changes to the flexibility calculated from measured modal parameters. But it has to be considered that these changes are often very small, as can be seen for instance in the example of a damage near the free end of the cantilever beam in section 4.2.2. A correct interpretation for damage detection can be complicated in case of measurement noise and in case temperature effects interfere whose impact can be higher than structural damage.
Conflict of Interests
The authors declare that there is no conflict of interest regarding the publication of this paper.
Acknowledgements
The authors acknowledge the high value contribution of Administration des Ponts et Chaussées Luxembourg, specially Mr. Gilles Didier et Gilberto Fernandes.
Cite this paper
Schommer, S., Mahowald, J., Nguyen, V.H., Waldmann, D., Maas, S., Zürbes, A. and De Roeck, G. (2017) Health Monitoring Based on Dynamic Flexibility Matrix: Theoretical Models versus In-Situ Tests. Engineering, 9, 37- 67. https://doi.org/10.4236/eng.2017.92004
References
- 1. Heylen, W., Lammens, S. and Sas, P. (1998) Modal Analysis Theory and Testing. 2nd Edition, Machine Design and Automation, Division of Production Engineering, Department of Mechanical Engineering, Faculty of Engineering, Katholieke Universiteit Leuven, Belgium.
- 2. Maia, N.M.M. and Montalvão e Silva, J.M. (1997) Theoretical and Experimental Modal Analysis. Research Studies Press, Wiley, Taunton, Somerset, England, New York.
- 3. Yan, A.-M. and Golinval, J.-C. (2005) Structural Damage Localization by Combining Flexibility and Stiffness Methods. Engineering Structures, 27, 1752-1761.
https://doi.org/10.1016/j.engstruct.2005.04.017 - 4. Duan, Z., Yan, G., Ou, J. and Spencer, B.F. (2005) Damage Localization in Ambient Vibration by Constructing Proportional Flexibility Matrix. Journal of Sound and Vibration, 284, 455-466.
https://doi.org/10.1016/j.jsv.2004.06.046 - 5. Load, B.D. (2002) Vectors for Damage Localization. Journal of Engineering Mechanics, 128, 7-14.
https://doi.org/10.1061/(ASCE)0733-9399(2002)128:1(7) - 6. Duan, Z., Yan, G., Ou, J. and Spencer, B.F. (2007) Damage Detection in Ambient Vibration Using Proportional Flexibility Matrix with Incomplete Measured DOFs. Structural Control and Health Monitoring, 14, 186-196.
https://doi.org/10.1002/stc.149 - 7. Perera, R., Ruiz, A. and Manzano, C. (2007) An Evolutionary Multiobjective Framework for Structural Damage Localization and Quantification. Engineering Structures, 29, 2540-2550.
https://doi.org/10.1016/j.engstruct.2007.01.003 - 8. Shih, H., Thambiratnam, D. and Chan, T. (2009) Vibration Based Structural Damage Detection in Flexural Members Using Multi-Criteria Approach. Journal of Sound and Vibration, 323, 645-661.
https://doi.org/10.1016/j.jsv.2009.01.019 - 9. Nobahari, M. and Seyedpoor, S.M. (2013) An Efficient Method for Structural Damage Localization Based on the Concepts of Flexibility Matrix and Strain Energy of a Structure. Structural Engineering and Mechanics, 46, 231-244.
https://doi.org/10.12989/sem.2013.46.2.231 - 10. Montazer, M. and Seyedpoor, S.M. (2014) A New Flexibility Based Damage Index for Damage Detection of Truss Structures. Shock and Vibration, 2014, 1-12.
https://doi.org/10.1155/2014/460692 - 11. Reynders, E. and De Roeck, G. (2010) A Local Flexibility Method for Vibration-Based Damage Localization and Quantification. Journal of Sound and Vibration, 329, 2367-2383.
https://doi.org/10.1016/j.jsv.2009.04.026 - 12. Yan, G., Duan, Z. and Ou, J. (2010) Damage Detection for Beam Structures Using an Angle-between-String-and-Horizon Flexibility Matrix. Structural Engineering and Mechanics, 36, 643-667.
https://doi.org/10.12989/sem.2010.36.5.643 - 13. Weng, S., Zhu, H.-P., Xia, Y. and Mao, L. (2013) Damage Detection Using the Eigenparameter Decomposition of Substructural Flexibility Matrix. Mechanical Systems and Signal Processing, 34, 19-38.
https://doi.org/10.1016/j.ymssp.2012.08.001 - 14. Chen, J.-T., Huang, W.-S., Lee, J.-W. and Tu, Y.-C. (2014) A Self-Regularized Approach for Deriving the Free-Free Flexibility and Stiffness Matrices. Computers & Structures, 145, 12-22.
https://doi.org/10.1016/j.compstruc.2014.07.024 - 15. Sung, S.H., Koo, K.Y. and Jung, H.J. (2014) Modal Flexibility-Based Damage Detection of Cantilever Beam-Type Structures Using Baseline Modification. Journal of Sound and Vibration, 333, 4123-4138.
https://doi.org/10.1016/j.jsv.2014.04.056 - 16. Masoumi, M., Jamshidi, E. and Bamdad, M. (2015) Application of Generalized Flexibility Matrix in Damage Identification Using Imperialist Competitive Algorithm. KSCE Journal of Civil Engineering, 19, 994-1001.
https://doi.org/10.1007/s12205-015-0224-4 - 17. Li, J., Wu, B., Zeng, Q.C. and Lim, C.W. (2010) A Generalized Flexibility Matrix Based Approach for Structural Damage Detection. Journal of Sound and Vibration, 329, 4583-4587.
https://doi.org/10.1016/j.jsv.2010.05.024 - 18. Perera, R., Ruiz, A. and Manzano, C. (2009) Performance Assessment of Multicriteria Damage Identification Genetic Algorithms. Computers & Structures, 87, 120-127.
https://doi.org/10.1016/j.compstruc.2008.07.003 - 19. Atashpaz-Gargari, E. and Lucas, C. (2007) Imperialist Competitive Algorithm: An Algorithm for Optimization Inspired by Imperialistic Competition. 2007 IEEE Congress on Evolutionary Computation, Singapore, 25-28 September 2007.
- 20. Stutz, L.T., Tenenbaum, R.A. and Corrêa, R. (2015) The Differential Evolution Method Applied to Continuum Damage Identification via Flexibility Matrix. Journal of Sound and Vibration, 345, 86-102.
https://doi.org/10.1016/j.jsv.2015.01.049 - 21. Wang, T., Zhang, L. and Tee, K.F. (2011) Ext raction of Real Modes and Physical Matrices from Modal Testing. Earthquake Engineering and Engineering Vibration, 10, 219-227.
https://doi.org/10.1007/s11803-011-0060-6 - 22. Mahowald, J. (2013) Evaluation of Dynamic Damage Indicators on Real-Life Civil Engineering Structures: Measurement Uncertainty and Environmental Influences Considered. PhD Dissertation, University of Luxembourg, Shaker, Aachen.
- 23. Pandey, A.K. and Biswas, M. (1995) Experimental Verification of Flexibility Difference Method for Locating Damage in Structures. Journal of Sound and Vibration, 184, 311-328.
https://doi.org/10.1006/jsvi.1995.0319 - 24. Gutermann, M. (2003) Ein Beitrag zur experimentell gestützten Tragsicherheitsbewertung von Massivbrücken. Dissertation, Technische Universität Dresden.
- 25. Scherbaum, F. and Mahowald, J. (2011) Report Bridge Champangshiehl 1+2. University of Luxembourg.
Nomenclature
[M], [C], [K]: Mass, damping and stiffness matrix;


Ω: Angular frequency of the input signal;

[R]: Residua matrix;






a: Scaling factor modal A;
[F]: Flexibility matrix.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact eng@scirp.org