Engineering
Vol.08 No.12(2016), Article ID:72536,6 pages
10.4236/eng.2016.812075
Effect of Nozzle Shaped Triangular Longitudinal Fins on Heat Transfer
Pulijala Shravya
Department of Mechanical Engineering, Birla Institute of Technology and Science (BITS), Hyderabad, India

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 26, 2016; Accepted: December 2, 2016; Published: December 5, 2016
ABSTRACT
Fins are used for enhancement of heat transfer. Triangular fins are arranged in form of nozzle and heat transfer coefficient is calculated. Angle of taper of nozzle is changed i.e. angles of triangles are varied and then heat transfer coefficient is calculated. Total finned area of all fins is almost the same. Number of fins and orientation of fins are different. In this study to calculate heat transfer coefficient of unfinned area open channel is considered where density and pressure are constant. This study shows that heat transfer is enhanced by 213%, 268% and 339% using 30˚, 45˚ and 60˚ fins. Computational results show that heat transfer is enhanced by 108%, 130%, 146% using 30˚, 45˚ and 60˚ fins.
Keywords:
Heat Transfer Enhancement, Fins, Triangular Longitudinal Fins

1. Introduction
Fins are used to enhance heat transfer. Fin is assumed to be long and mL = 5 where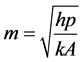 , i.e. efficiency is maximum at that length. I.e., a material of low thermal con-
, i.e. efficiency is maximum at that length. I.e., a material of low thermal con-
ductivity has been chosen. Increase in number of fins increases heat transfer because surface area increases. In this study number of fins and orientation of fins is changed keeping surface area of finned and unfinned area of all specimens constant.
2. Literature Survey
Leonard D. Tijing et al. (2006) studied heat transfer enhancement using straight and twisted internal fin inserts [1] . Li-Min Chang et al. (2009) studied relationship between heat transfer enhancement and absolute vorticity flux along main flow direction in a channel formed by a flat tube bank fin with vortex generators [2] . Andrew J. L. Foong (2009) studied laminar convective heat transfer in a micro channel with internal longitudinal fins [3] . Balaram Kundu (2006) studied performance and optimum design analysis of longitudinal and pin fins with simultaneous heat and mass transfer [4] : Unified and comparative investigations. A.A. Joneidi et al. (2009) studied differential trans- formation method to determine fin efficiency of convective straight fins with temperature dependent thermal conductivity [5] . J. M. Wu et al. (2007) investigated laminar convective heat transfer in fin-and-tube heat exchanger in aligned arrangement with longitudinal vortex generator from the viewpoint of field synergy principle [6] . J. F. Fan et al. (2008) studied a performance evaluation plot of enhancement heat transfer techniques oriented for energy saving [7] . S. C. Haldar et al. (2007) studied laminar free convection about a horizontal cylinder with longitudinal fins of finite thickness [8] .
3. Experimental Setup
In this study a cylinder of diameter 1 m is considered. Triangular fins are arranged in form of nozzle. Thickness of fin is uniform. For 30˚ isosceles triangle sides are 0.5, 0.5, 0.866025403, for 45˚ isosceles triangle sides are fins are 0.7071067, 0.433012 and 0.433012 and for 60˚ isosceles triangle sides are 0.288675, 0.288675 and 0.288675. Altitude of all fins is same. Number of fins that fit the specimen is calculated by equating finned area of all specimens. The number of fins that fit is 3, 4 and 10 respectively for 30˚, 45˚ and 60˚ triangles. After finding number of fins, they are arranged on specimen in form of nozzle. Flow is along surface and velocity at inlet of nozzle shaped channel is 10 m/s.
4. Solution Methodology
After finding finned and unfinned area heat transfer coefficient of specimen is calculated from Nusselt number. Since Gr/Re2 is lesser than one, it is assumed that forced convection occurs.
Equation (1) is used when flow is along the surface and fluid is non bouyant. Eg flow over flat plate. Equation (2) is used when fin is finite and without tip insulation.
For finned region
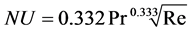 (1)
(1)
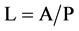
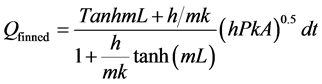 (3)
(3)
For unfinned area average velocity is calculated using continuity equation.
Mass flow is enhanced due to reduction of area. For 30˚, 45˚, 60˚ average velocities are 33 m/s, 55 m/s, 66.5 m/s. Computational results show that average velocity is around 10 m/s. For unfinned area open channel flow is considered. i.e. pressure and density are constant. Average velocity is used in calculation of Nusselt number.
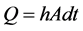
Nusselt number for finned and unfinned area is calculated from Equation (1). From nusselt number heat transfer coefficient is calculated. It is assumed that mL = 5 and efficiency of fin is maximum. It is assumed that buoyant force is negligible and hot air leaves along the surface.
Pressure is constant and kinetic energy is used to overcome friction. Heat flowing out is calculated from Equation (2) for finned area and Equation (3) for unfinned area.
5. Results
Forced convection occurs in all cases. Velocity at each section of unfinned region is calculated by continuity equation. Computational results show that even though the total finned area of three specimens are same the heat transfer coefficient increases with increase in angle of triangles from 30˚ to 60˚. This due to enhancement of flow velocity due to nozzle shaped arrangement. Table 1 shows theoretical results.
In Table 1 heat transferred for single fin and spacing is calculated from Nusselt number. The computational analysis of the three specimens shows that there are no high stress regions due to presence of triangular fins.
Figures 1-3 show the temperature contour of specimens.
The figures show reduced temperature due to heat transfer because of fins.
This study shows that heat transfer is enhanced by 213%, 268% and 339% using 30˚, 45˚ and 60˚ fins. Table 2 shows the calculation. Total heat transferred from both finned area and unfinned area is calculated and divided by heat transferred without using fin. Thus effectiveness of fin is obtained. Computational results show only slight increase in velocity in unfinned area. Heat transfer coefficient in finned area is expected to be higher than calculated value due to rise in velocity.
6. Conclusion
In unfinned region, the passage is in form of nozzle. It is expected that velocity rises
Table 1. Calculation of heat transferred for one fin and corresponding spacing.
Figure 1. 30˚ longitudinal triangular fins.
Figure 2. 45˚ longitudinal fins.
Table 2. Calculation of effectiveness of fins.
Figure 3. 60˚ longitudinal fins.
according to continuity equation. Since it is an open channel there is only slight rise in velocity. In unfinned area, average velocity of 10 m/s is used in calculation of Nusselt number for obtaining computational value of heat transferred. For finned area there is rise in velocity but average value of 10m/s is used in calculation. Actual values are expected to be higher than computational values. Table 1 shows the values.
There is forced convection in all cases. There is change in number and Orientation of fins. Heat transfer is enhanced by increase in mass transfer. Computational study shows that average temperature is lowered in all finned triangle specimens. Dark blue shows that temperature is lowered due to fins and temperature stresses are minimum. This study shows that heat transfer is enhanced by 213%, 268% and 339% using 30˚, 45˚ and 60˚ fins. Computational results show that heat transfer is enhanced by 108%, 130%, 146% using 30˚, 45˚ and 60˚ fins.
Acknowledgements
I thank my guide S. S. Deshmukh for supervising my work.
Cite this paper
Shravya, P. (2016) Effect of Nozzle Shaped Triangular Longitudinal Fins on Heat Transfer. Engineering, 8, 831-836. http://dx.doi.org/10.4236/eng.2016.812075
References
- 1. Tijing, L.D., Pak, B.C., Baek, B.J. and Lee, D.H. (2006) A Study on Heat Transfer Enhancement Using Straight and Twisted Internal Fin Inserts. International Communications in Heat and Mass Transfer, 33, 719-726.
https://doi.org/10.1016/j.icheatmasstransfer.2006.02.006 - 2. Chang, L.-M., Wang, L.-B., Song, K.-W., Sun, D.-L. and Fan, J.-F. (2009) Numerical Study of the Relationship between Heat Transfer Enhancement and Absolute Vorticity Flux along Main Flow Direction in a Channel Formed by a Flat Tube Bank Fin with Vortex Generators. International Journal of Heat and Mass Transfer, 52, 1794-1801.
https://doi.org/10.1016/j.ijheatmasstransfer.2008.09.029 - 3. Foong, A.J.L., Ramesh, N. and Chandratilleke, T.T. (2009) Laminar Convective Heat Transfer in a Micro Channel with Internal Longitudinal Fins. International Journal of Thermal Sciences, 48, 1908-1913.
https://doi.org/10.1016/j.ijthermalsci.2009.02.015 - 4. Kundu, B. (2007) Performance and Optimum Design Analysis of Longitudinal and Pin Fins with Simultaneous Heat and Mass Transfer: Unified and Comparative Investigations. Journal of Applied Thermal Engineering, 27, 976-987.
https://doi.org/10.1016/j.applthermaleng.2006.08.003 - 5. Joneidi, A.A., Ganji, D.D. and Babaelahi, M. (2009) Differential Transformation Method to Determine Fin Efficiency of Convective Straight Fins with Temperature Dependent Thermal Conductivity. Journal of International Communications in Heat and Mass Transfer, 36, 757-762.
- 6. Wu, J.M. and Tao, W.Q. (2007) Investigated Laminar Convective Heat Transfer in Fin-and-Tube Heat Exchanger in Aligned Arrangement with Longitudinal Vortex Generator from the Viewpoint of Field Synergy Principle. Journal of Applied Thermal Engineering, 27, 2609-2617.
- 7. Fan, J.F., Ding, W.K., Zhang, J.F., He, Y.L. and Tao, W.Q. (2008) Study of a Performance Evaluation Plot of Enhancement Heat Transfer Techniques Oriented for Energy Saving. International Journal of Heat and Mass Transfer, 52, 33-44.
https://doi.org/10.1016/j.ijheatmasstransfer.2008.07.006 - 8. Haldar, S.C., Kochhar, G.S. and Manohar, K. (2007) Laminar Free Convection about a Horizontal Cylinder with Longitudinal Fins of Finite Thickness. International Journal of Thermal Science, 46, 692-698.
https://doi.org/10.1016/j.ijthermalsci.2006.10.001





