Engineering
Vol.07 No.11(2015), Article ID:61004,9 pages
10.4236/eng.2015.711064
Computational Study on Effect of Variation of Pitch-Chord on Secondary Losses in Rectilinear Turbine Cascade
Pulijala Shravya
Department of Mechanical Engineering, Birla Institute of Technology and Science, Pilani, India

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 19 September 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT
Losses in turbine cascade are categorized as profile loss, secondary loss, tip clearance loss and annulus loss. Profile loss occurs due to development of boundary layer on surface of blade [1] . Increase in thickness of boundary layer and adverse pressure gradient increases profile loss. Secondary loss occurs due to turning of flow through flow passage which results in blowing of energy from pressure side to suction side. In turbine rotor blade suction surface leads and tip clearance loss occurs due to leakage of air from pressure side to suction side of the blade through tip clearance. Annulus loss occurs due to development of boundary layer on stationary row of blade. It also occurs in moving row of blade but in moving row of blades boundary layer is scraped by flow over the blades. This paper presents effects of variation of pitch-chord ratio on secondary loss.
Keywords:
Turbine Cascade, Pitch-Chord Ratio, Secondary Losses

1. Introduction
Secondary losses occur because of unwanted loss of energy due to formation of vortices and turning of flow [2] . The pressure gradient is not uniform due to formation of boundary layer on the blade surface, tip leakage, formation of boundary layer on end walls, abrupt change in area of curved blade passage, viscous losses etc. Flow is retarded at walls due to viscous losses, as a result pressure increases and velocity is reduced to zero. When the area of curved passage increases, pressure rises and flow is decelerated. This causes increase in thickness of boundary layer at walls.
When area of passage decreases, flow is accelerated and thickness of boundary layer decreases. Since the flow passage is curved, velocity changes due to change in direction of flow. It is assumed that flow follows the blade passage and some energy is lost in changing direction of flow. This results in variation of pressure. The suction surface and pressure surface of blade are not symmetric, so pressure on suction side is different from pressure on pressure side of aerofoil. All these contribute to variation of pressure as flow proceeds through passage. This results in formation of vortices. Loss of energy occurs due to these vortices, resistance to flow and adverse pressure gradient.
2. Literature Survey
Langston et al. (1977), Marchal and Sieverding (1977), Sharma and Buttler (1987), Hodson and Dominy (1987) and Yamamotto (1987) clarified details of three dimensional flow development [3] [4] . Moore and Adhye (1985) and Gregory smith et al. (1988) analyzed loss production mechanisms. Moore et al., Zunino et al., Gregory Smith et al. (1982) and Cleak (1990) determined the effect of turbulence quantities. Yamamoto and Nouse (1988) have shown the influence of incidence angle on the three-dimensional flow inside a linear cascade. Hodson and Dominy have reported on secondary flows downstream of high speed linear cascade under off-design conditions, including incidence angle, pitch-chord ratio, Reynolds number and inlet boundary layer thickness variations. Hodson and Dominy have tested performance of low pressure turbine cascade at pitch chord ratios of 0.46, 0.56, and 0.69.
Experiments carried out at (Centro Nazionale per Ricerche Sulla propulsione e sull’ Energetica, Milano) CNPM laboratory by Antonio Perdichizzi, Marco Savini and Vincenzo Dossena (1999) on secondary flows in turbine cascade at pitch-chord ratios of 0.58, 0.73, and 0.87. The secondary kinetic energy grows considerably as the pitch chord ratio increases. Experiment was performed on transonic wind tunnel [5] .
Young J. Moon et al. (2000) analyzed the effect of end wall fencing for reducing the secondary flow using k-ξ turbulence model. They also justified the optimized positioning of the end wall fencing for reducing the secondary flow losses, because the end wall fencing prevents the merging of pressure side horse shoe vortex with the passage vortex and hence total pressure loss decreases [6] . Saha et al. (2008) analyzed the turbulent flow through a three dimensional non-axisymmetrical blade passage and observed that end wall contouring reduces the pitch wise pressure gradient near the end wall which reduces the chances of flow separation.
Sonoda et al. (2009) used axi-symmetrical end wall contouring method for reducing the secondary losses in high pressure turbine having low aspect ratio. Brear et al. (2002) tried to reduce this pressure surface separation by modifying the leading edge geometry.
They concluded that increasing the blade thickness at the pressure surface decrease the strength of secondary flow by increasing the momentum near the wall. Shih et al. (2003) observed effects of leading-edge airfoil fillet on the flow in a turbine. The increased size of the stagnation zones on the end walls about the airfoil’s leading edge lowers the flow speed and velocity gradients there, which in turns reduces turbulence production. Mahmood et al. (2007) studied the secondary structure in a blade passage with and without leading edge fillet and observed that the size and strength of the passage vortex become smaller with the fillets.
Korakianitis et al. (2010) have proposed a direct design method based on specifying blade surface-curvature distributions so as to minimize the chances of flow separation [7] . Lei et al. (2011) analyzed the effect of leading edge modification on the secondary loss. They used vortex generator for introducing counter rotating vortex which oppose the passage vortex and hence reduce the secondary flow losses. Stream wise end wall fences were employed by Kawai (1994), Moon and Koh (2001), and Govardhan et al. (2006).
Secondary loss predicted in various loss models had significantly different behaviours. It can be found that the secondary losses predicted in the AMDC and K-O models were almost constant with the variation of pitch- chord ratio while the loss predicted in the C-C model rises with increase in pitch-chord ratio. This is because the influence of the pitch-chord variation on the secondary loss is not taken into account in the final secondary loss models of the AMDC and K-O. Ainley/Mathieson and Dunham/Came (AMDC), Kacker/Okapuu (K-O) and Craig/Cox (C-C) were compared by Ning (2000) [8] .
3. Research Question
What is effect of variation of Pitch-chord ratio on seconadary losses in rectilinear stationary turbine cascade?
4. Experimental Setup
A profile 6030 blade is chosen and a cascade is made using Ansys Work bench using two blades forming three similar flow passages. Figure 1 shows profile of profile 6030 turbine blade. Upper and lower wall of cascade near test section resemble pressure surface and suction surface of blade. The side walls are plane. Figure 2 shows cascade geometry. Chord of blade is 50 mm. Stagger angle is 70˚ degrees. Height of blade is 95 mm. Figure 3 shows profile 6030 straight blade. In front of cascade a compressor is placed. At inlet to cascade the pressure is 10 atm and velocity is 102 m/s. At exit of test section flow is assumed to follow flow passage. Exit of cascade is open to atmosphere. Wall of cascade is isothermal and temperature is maintained at 25˚ Celsius. Tip clearance is 5.26% of blade height. Inlet flow angle is 55˚ degrees and outlet angle of blade is 45˚ degrees. Since cascade is stationary it is assumed that flow follows the passage at trailing edge of blade [9] . Fluid used is air.
Pitch of the blade is varied and effect of variation of pitch on secondary losses is studied.
5. Solution Methodology
In turbine flow is accelerated so boundary layer technique cannot be used to solve flow equations. Navier-stokes equations are formed considering viscous forces, pressure forces, body forces and gravitational force. Surface
Figure 1. Profile of blade.
Figure 2. Cascade.
Figure 3. Blade.
tension force is negligible. To introduce turbulent forces or Reynolds stresses Navier stokes equations are time averaged and two equation turbulence model (K-ε model) is introduced into the transport equation. The equations are solved using Runge-Kutta algorithm. Unstructured grid is generated using tetrahedra, pyramids and prisms. Grid refinement technique is used to minimize global and local error.
Since the turbulence level is less than 5% flow is assumed to be steady. The flow passage, leaving the areas very close to the wall in test section, is divided into stream tubes whose inlet and exit areas are equal to 0.004 m × 0.010 m. The variation of velocity in passage is small so stream tubes are assumed to be of equal areas. The control volumes are not chosen since the mass flow across the control surface is not known.
The value of pressure and velocity at leading edge and trailing edge of blade are taken for each stream tube. The values of lift force, drag force, coefficient of lift, and coefficient of drag are calculated. Secondary loss coefficient is calculated using corrected Vavra equation.
6. Corrected Vavra’s Equation by Lakshminarayana and Horlock for Turbine Blades
It is difficult to measure secondary losses experimentally. Non dimensional coefficient obtained from various parameters is used. The constants are obtained from experimental results. Total loss is measured by measuring inlet and exit parameters. Profile losses and other losses are measured experimentally and are subtracted from total loss to obtain secondary losses. Corrected Vavra’s relation is explicit in nature and simple [10] .
 (1)
(1)
 (2)
(2)
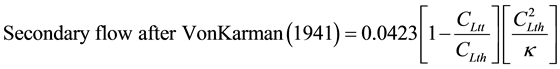 (3)
(3)
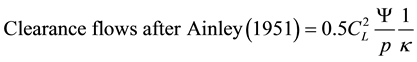 (4)
(4)
CL = Coefficient of lift;
κ = aspect ratio;
P = Pitch of blade;
α = Blade tip clearance height;
Cltt = Coefficient of lift at tip;
Clth = Coefficient of lift at hub.
Equation (2) is non-dimensional quantity which has blade loading, aspect ratio of blade and flow turning angle as parameters. In case of lifting flow blade loading is a function of coefficient of lift.
Equation (3) is non-dimensional correction added to Equation (2). Coefficient of lift is different at different points along span. Ratio of difference of lift coefficient at extreme ends along span to Lift coefficient at hub is multiplied with Equation (2) along with correction for change in exit angle to obtain Equation (3). Value of Lift coefficient is usually high at hub and decreases towards tip.
Equation (4) shows the effect of variation of tip clearance height on secondary losses. Tip leakage losses increase with increase in tip clearance height. If tip clearnce is large secondary losses are reduced due to interaction of tip vortex with passage vortex (Table 1).
7. Effect of Variation of Pitch-Chord Ratio on the Pressure and Velocity at Trailing Edge of Blade
Usually in a stationary turbine cascade there is increase in velocity and decrease in pressure from leading edge to trailing edge of blade. This is not contradictory to results obtained at various pitch-chord ratios except 0.42 and 0.44.
At pitch-chord ratio of 0.42 and 0.44 there is an increase in pressure from leading edge to trailing edge. This is contradictory to usual observation.
At these two values of pitch-chord ratio at leading edge there is formation of expansion shock wave as a result of which there is drop in pressure, increase in velocity and there is large amount of loss in head. The velocity increases and becomes supersonic after expansion shock wave at leading edge of blade. As the supersonic fluid
Table 1. Values of secondary loss coefficients.
passes through blade pressure increases from leading edge to trailing edge. This happens because the pressure of supersonic fluid increases in converging passage.
Average pressure and average velocity at leading edge are nearly same. Average density at leading edge is nearly same. Exit pressure contours and exit velocity contours for various values of pitch are different. The area of flow passage is different for various values of pitch. Flow in narrow passage is more uniform than broader passage. The pressure losses in broader passages are more than narrow passages. This results in variation of pressures at trailing edge with variation of pitch. The variation of area of passage and mass flow results in variation of pressure and velocity at trailing edge with variation of pitch.
8. Variation of Lift Force with Variation of Pitch
Variation of lift force with variation of pitch is shown by Figure 4 excluding the pitch chord ratios of 0.42 and 0.44 since, the value of lift force is high.
The value of lift force increases with increase in pitch. Since the pitch of the blade is varied, area at leading edge is different and the mass flow rate is different. The inlet boundary conditions are same. Lift force depends on pressure gradient from pressure surface to suction surface of blade. As the passage becomes broader the flow becomes more non uniform. As a result greater pressure gradients are developed this results in increase in value of lift force as the pitch of blade is varied.
At pitch chord ratios of 0.42 and 0.44 lift force drastically increases. The direction of lift force is opposite when compared with other values of pitch blades.
9. Variation of Drag Force with Variation of Pitch
Variation of drag force with variation of pitch is shown by Figure 5 excluding the pitch chord ratios of 0.42 and 0.44 since the value of drag force is high. There is a variation in pressure at trailing edge with variation of pitch, which results in variation of pressure drag. There is a variation of velocity at trailing edge for various values of pitch this results in variation of frictional drag. Thus total drag force varies with variation of pitch. At pitch chord ratios of 0.42 and 0.44 drag force drastically increases because at these values of pitch pressure increases from leading edge to trailing edge and the inlet and exit velocities are supersonic. Frictional losses are high due to adverse pressure gradient. There is high pressure at trailing edge which causes high pressure drag. Since the velocities are supersonic there is high frictional drag. Thus the total drag is high. The value of frictional drag increases due to increase in velocity. High frictional losses produce heating effect.
10. Variation of Coefficient of Lift (CL) with Variation of Pitch of Blade
Variation of coefficient of lift with variation of pitch is shown by Figure 6 excluding the pitch chord ratios of 0.42 and 0.44. The losses due to formation of boundary layer on end walls, cross flows, tip clearance effect affect the value of coefficient of lift. Dynamic head varies for various values of pitch due to variation of mean av
Figure 4. Variation of lift force.
erage velocity and density at trailing edge. Value of lift force varies with variation of pitch. Thus the value of coefficient of lift varies.
At pitch chord ratios of 0.42 and 0.44 coefficient of lift is low. At these values of pitch, pressure increases from leading edge to trailing edge as inlet and exit velocities are supersonic. Even though the value of lift force is high, the coefficient of lift is small as dynamic head is high.
11. Variation of Coefficient of Drag (CD) with Variation of Pitch of Blade
Variation of coefficient of drag with variation of pitch is shown by Figure 7 excluding the pitch chord ratios of
Figure 5. Variation of drag force.
Figure 6. Variation of coefficient of lift.
Figure 7. Variation of coefficient of drag.
0.42 and 0.44. Variation of pressure and velocity contours for various values of pitch result in variation of drag force and dynamic head. This results in variation of coefficient of drag.
At pitch chord ratios of 0.42 and 0.44 coefficient of drag is high. At this value of pitch, pressure increases from leading edge to trailing edge of blade and inlet and exit velocities are supersonic. Because of adverse pressure gradient the frictional losses are high and coefficient of drag is high.
12. Variation of Lift Force (L), Drag Force (D), Coefficient of Lift (CL) Coefficient of Drag (CD) along SPAN
Readings are taken for pitch chord ratios of 0.32, 0.34, 0.36, 0.38, 0.4, 0.42, 0.44, 0.46, 0.48, 0.5, 0.52, 0.54, 0.56, 0.6, 0.64, 0.68, 0.7, 0.72, 0.76 and 0.8. Values of lift force and drag force at various points along span is noted for various values of pitch. Coefficient of lift, coefficient of drag at various points along span is calculated for each value of pitch.
Exit pressure contours and exit velocity contours for various values of pitch are different. Variation of lift force and drag force along span is usually high for higher values of pitch, since flow is more non uniform in broader passage.
13. Variation of Secondary Loss Coefficient with Variation of Pitch of Blade
As pitch increases area of passage increases and flow through a broad passage is more non-uniform than flow through narrow passage. The formation of boundary layers at walls, tip leakage effect, viscous losses result in variation of pressure and velocity along span and pitch of blade.
The non uniform pressure gradients indicate secondary losses. Value of lift coefficient indicates pressure side to suction side pressure gradient so it also indicates secondary loss. Variation of pressure along pitch causes lift force.
Variation of pressure along pitch and span causes variation of pressure drag and variation of lift force. Variation of velocity along pitch and span of blade causes variation friction drag. So variation of pressure along span is indicated by variation of lift force and drag force along span. Thus variation of lift force and drag force along span indicates the amount of secondary loss. Variation of secondary losses with variation of pitch is shown by Figure 8 excluding the pitch chord ratios of 0.42 and 0.44.
These pitch-wise and span-wise pressure gradients caused by turning of flow indicate secondary losses. The value of coefficient of lift and variation of lift and drag forces along span are usually high for higher values of pitch due to increased non uniformity of flow. The value of secondary loss coefficient is usually high for higher values of pitch.
Loss of head from inlet of compressor to test section (before leading edge) is negligible.
14. Conclusions
Value of secondary loss is indicated by value of coefficient of lift and variation of lift and drag force along span
Figure 8. Variation of secondary loss coefficient.
which depends upon pitch-wise and span wise pressure gradients. Secondary losses are usually high for higher values of pitch.
Although the secondary losses for rotor are higher than stationary cascade, this analysis helps in setting lower limit for pitch-chord ratio. The lower limit is highest value of pitch-chord ratio at which expansion shock losses occur due to rapid reduction of pressure plus the safety margin. It also helps in choosing an upper limit if remaining losses are also considered.
Since it is computational analysis, it saves money.
Acknowledgements
I am grateful to my guide Mr. V Uma Maheshwar for supervising my work.
Cite this paper
PulijalaShravya, (2015) Computational Study on Effect of Variation of Pitch-Chord on Secondary Losses in Rectilinear Turbine Cascade. Engineering,07,733-741. doi: 10.4236/eng.2015.711064
References
- 1. Hodson, H.P. and Dawes, W.N. (1998) On the Interpretation of Measured Profile Losses in Unsteady Wake-Turbine Blade Interaction Studies. Journal of Turbomachinery, 120, 276-284.
- 2. Yahya, S.M. Turbines, Compressors and Fans. Tata McGraw Hill Education Private Limited, New Delhi.
- 3. Hodson, H.P. and Dominy, R.G. (1987) Three-Dimensional Flow in a Low-Pressure Turbine Cascade at Its Design Condition. Journal of Turbomachinery, 109, 177-185.
http://dx.doi.org/10.1115/1.3262083 - 4. Becz, S., Majewski, M.S. and Langston, L.S. (2003) Leading Edge Modification Effects on Turbine Cascade Endwall Loss. ASME Proc. Turbo Expo, GT-2003-38898.
http://dx.doi.org/10.1115/gt2003-38898 - 5. Luo, J.Q., Xiong, J.T. and Liu, F. and McBean, I. (2010) Secondary Flow Reduction by Blade Redesign and Endwall Contouring Using an Adjoint Optimization Method. Proceedings of ASME Turbo Expo 2010: Power for Land, Sea and Air GT 2010, Glasgow, 14-18 June 2010.
- 6. Mahmood, G.I., Gustafson, R. and Acharya, S. (2005) Experimental Investigation of Flow Structure and Nusselt Number in a Low Speed Linear Blade Passage With and Without Leading Edge Fillets. Journal of Heat Transfer, 127, 499-512.
http://dx.doi.org/10.1115/1.1865218 - 7. Singoria, V.K. and Samsher (2013) The Study of End Losses in a Three Dimensional Rectilinear Turbine Cascade. Journal of Emerging Technology and Advanced Engineering, 3, 782.
- 8. Ning, W.E.I. (2000) Significance of Loss Models in Aerothermodynamic Simulation for Axial Turbines. Doctoral Thesis.
- 9. Cohen, H., Rogers, G.F.C. and Saravanamuttoo, H.I.H. Gas Turbine Theory. 4th Edition, Longman Group Ltd., Essex, 19.
- 10. 10Wood, J.R. (1972) An Investigation of Secondary-Flow Phenomena and Associated Losses in a High-Deflection Turbine Cascade. Naval Postgraduate School, Monterey.










