Engineering
Vol.07 No.10(2015), Article ID:60342,12 pages
10.4236/eng.2015.710054
Turbulent Modulation in Particulate Flow: A Review of Critical Variables
Ammar Saber1,2, T. Staffan Lundström1, J. Gunnar I. Hellström1
1Fluid and Experimental Mechanics Division, Luleå University of Technology, Lulea, Sweden
2Mechanical Engineering Department, University of Mosul, Mosul, Iraq
Email: ammar.hazim@ltu.se, staffan.lundstrom@ltu.se, gunnar.hellstrom@ltu.se
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2015; accepted 13 October 2015; published 16 October 2015
ABSTRACT
A review of the main mechanisms influencing turbulent modulation in the presence of spherical and non-spherical particles is presented. The review demonstrates the need for more numerical and experimental work with higher accuracy than obtained so far and the need to resolve the flow near the surface of particles with the aim to re-evaluate the quantitative effect of different parameters on turbulent modulation. The review reveals that non-spherical particles have more adverse effect on turbulence as compared to spherical ones, for the same ambient conditions.
Keywords:
Two Phase Flow, Turbulent Modulation, Non-Spherical Particle, Stokes Number, Particle Reynolds Number, Length Scale, Density Ratio

1. Introduction
Turbulent flows can be found everywhere in nature and industry, but a unifying theory of turbulence does not exist. When spherical particles are suspended into such a flow, the flow becomes even more intricate and the resulting interactions between the particles and turbulent structures are not fully understood. For non-spherical particles that often appear in fluids in industrial processes, like paper making, iron ore pelletization, pneumatic conveying [1] , cyclone filters [2] [3] , and biomass gasification and combustion, the interactions of the particles and the fluid in turbulent flow are extremely complex while theories exists for creeping flow [4] -[8] . In turbulent flow, the particles will wobble or move chaotic, depending on their size and density [9] . Hence, the carrier phase turbulence alters the dispersed phase translational and rotational motion and the particles influence the detailed and overall flow of the carrier phase.
It is important to study turbulent modulation, or in other words the influence of the dispersed phase on the carrier phase due to its large effect on the behavior and performance of many industrial systems involving solid- gas flow. Already in the middle of the former century, researchers high-lighted that the presence of particles can significantly influence the rate of, for instance, heat transfer and chemical reaction. Such features can be explained with turbulent modulation. The study of turbulent dispersion in two-phase flows has a long history as described for spherical particle motion in [10] and for non-spherical particle motion in [11] while studies on the physics of how the particles effect the fluid turbulence has gained less attention over the last few decades [12] and is still an open topic. To achieve a valuable mathematical description for issues such as turbulent combustion or chemical processes involving solid-gas flow for computational fluid dynamic CFD codes, the knowledge and understanding of the mutual interaction between phases should be improved before additional relationships such as chemical reactions are included.
In two phase two-way coupling flow several mechanisms contribute to the modification of the turbulence like additional dissipation caused by the particles, the transfer of a portion of particle kinetic energy to the carrier phase, turbulence due to vortex shedding behind the particles and increase of dissipation due to no-slip boundary conditions at the surface of the particles. Secondary motion, due to the higher degree of freedom of motion, associated with non-spherical particles can transfer kinetic energy into Turbulent Kinetic Energy TKE in more moods than spheres. The importance of each of these mechanisms for turbulent modulation will now be discussed regarding both rigid spherical and non-spherical particles.
2. Two-Phase Flow Turbulence Modulation
The addition of particles to the carrier phase tends to affect the TKE, dissipation rate, and turbulence intensity. Many researchers have categorized the alterations in turbulence into augmentation and attenuation and suggested correlations that quantitatively describe these phenomena. In general, observations suggest that small particles attenuate the turbulence of the carrier phase and large particles amplify it [13] . It can be argued that a heavy particle sinking in a fluid at rest will transfer its potential energy to the fluid around it and that particles moving in turbulent flow maybe seen in a similar manner where both kinetic and potential energy may be transferred to the surroundings. On the other hand, heavy particle in turbulent flow needs energy if they are to be moved in the direction of flow but it is not obvious how the TKE production and dissipation will be affected. In vertical up-flow, gravity and buoyancy will play major roles and heavy particles attenuate the kinetic energy. A point-particle approach is a sound tactic when the particle diameter dp is smaller than the Kolmogorov length scale η. For a large number of particles fully resolved simulations are, however, not possible to carry out [10] [14] . In the case of non-spherical particles, the shape effect of particles on the solid-liquid turbulence interaction has been investigated for particles with a diameter almost equal to the Taylor micro-scale and with a small relative density,
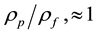 [15] . One result was attenuation in TKE of 3% and 15% for prolate ellipsoidal particles and spherical particles, respectively. A spectral analysis showed that the ellipsoidal particles distributed more TKE to the smaller scales with less energy loss than the spherical particles. Capone [16] injected rod-like particles into a fully developed water jet, which resulted in a significant change in turbulent structure. Mandø [17] investigated turbulence intensity modulation for spheres, discs and prolate ellipsoids. The results indicate that the discs and the prolate spheroids cause more attenuation than the spherical particles. In most of non- spherical particle studies, particles dampen turbulence more than spherical particles and amplify turbulence less than spherical particles. This may partly be related to non-suitable parameters used to compare spherical and non-spherical particles or related to the preferential orientation and rotation of particles that affect the formation of the wake behind the particles. A summary of published results on different types of particles is presented in Table 1.
[15] . One result was attenuation in TKE of 3% and 15% for prolate ellipsoidal particles and spherical particles, respectively. A spectral analysis showed that the ellipsoidal particles distributed more TKE to the smaller scales with less energy loss than the spherical particles. Capone [16] injected rod-like particles into a fully developed water jet, which resulted in a significant change in turbulent structure. Mandø [17] investigated turbulence intensity modulation for spheres, discs and prolate ellipsoids. The results indicate that the discs and the prolate spheroids cause more attenuation than the spherical particles. In most of non- spherical particle studies, particles dampen turbulence more than spherical particles and amplify turbulence less than spherical particles. This may partly be related to non-suitable parameters used to compare spherical and non-spherical particles or related to the preferential orientation and rotation of particles that affect the formation of the wake behind the particles. A summary of published results on different types of particles is presented in Table 1.
3. Scaling of Turbulence Modulation
In the context of turbulence modulation the carrier phase may be characterized and described by its physical properties in addition to the turbulent length and time scales, dissipation and TKE of the flow. The dispersed phase, in its turn, can in addition to particle shape be described by particle density, size, surface and volume/ mass fraction. Hence, a number of relationships can be formed that may be of importance. For qualitative evaluation of turbulence modulation the Stokes number St, the particle Reynolds number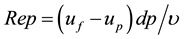 , and the ratio of dp to turbulent length scales are frequently applied. Here also η may play a role. To determine the magnitude of the modulation, the mass loading ratio and volume fraction of particles may be used. Recently,
, and the ratio of dp to turbulent length scales are frequently applied. Here also η may play a role. To determine the magnitude of the modulation, the mass loading ratio and volume fraction of particles may be used. Recently,
Table 1. Previous experimental work.
Tanaka and Eaton [18] introduced a new dimensionless particle momentum number derived from the particle- laden Navier-Stokes Equations. For non-spherical particles additional parameters are introduced to describe new features that come into play like particle shape, aspect ratio and mass distribution.
4. Stokes Number
The Stokes number
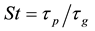 denotes how well the particles are able to follow alterations in the magnitude and direction of the flow where
denotes how well the particles are able to follow alterations in the magnitude and direction of the flow where
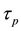 is the time it takes for a particle to accelerate from rest to a velocity being 63% of the ambient flow velocity and
is the time it takes for a particle to accelerate from rest to a velocity being 63% of the ambient flow velocity and
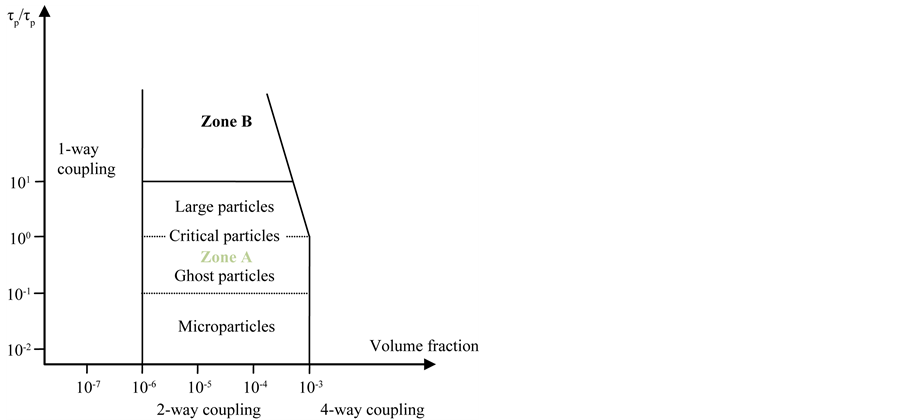
 is the carrier phase time scale. For St less than unity the particles just follow the streamlines while for St larger than one the particles detach from the flow. For particles of St ≈ 1, St can be used to describe the alteration of the carrier phase turbulence. For small particles dp ~ η, observations yield an increases in the rate of TKE dissipation and a corresponding reduction of turbulence for St = O(1) ~ O(10), hence the particles extract the turbulent energy from the flow and dissipate it. Elgobashi et al. [19] used a two-way coupling approach to study the TKE production and dissipation for a system with small spherical particle, Rep ≤ 1 and St based on the Kolmogorov time scale τη ≈ O(10−2) to O(101). The aim was to update previous results, especially regarding small particles, Zone A in Figure 1, and they found that TKE and its dissipation rate ԑ are function of St. Luo Fan et al. [20] studied a two phase solid-gas jet flow by developing a DNS technique with a two-way coupling method at moderate Re and St = 0.01, 1 and 50. They found attenuation in TKE for the cases that were studied.
is the carrier phase time scale. For St less than unity the particles just follow the streamlines while for St larger than one the particles detach from the flow. For particles of St ≈ 1, St can be used to describe the alteration of the carrier phase turbulence. For small particles dp ~ η, observations yield an increases in the rate of TKE dissipation and a corresponding reduction of turbulence for St = O(1) ~ O(10), hence the particles extract the turbulent energy from the flow and dissipate it. Elgobashi et al. [19] used a two-way coupling approach to study the TKE production and dissipation for a system with small spherical particle, Rep ≤ 1 and St based on the Kolmogorov time scale τη ≈ O(10−2) to O(101). The aim was to update previous results, especially regarding small particles, Zone A in Figure 1, and they found that TKE and its dissipation rate ԑ are function of St. Luo Fan et al. [20] studied a two phase solid-gas jet flow by developing a DNS technique with a two-way coupling method at moderate Re and St = 0.01, 1 and 50. They found attenuation in TKE for the cases that were studied.
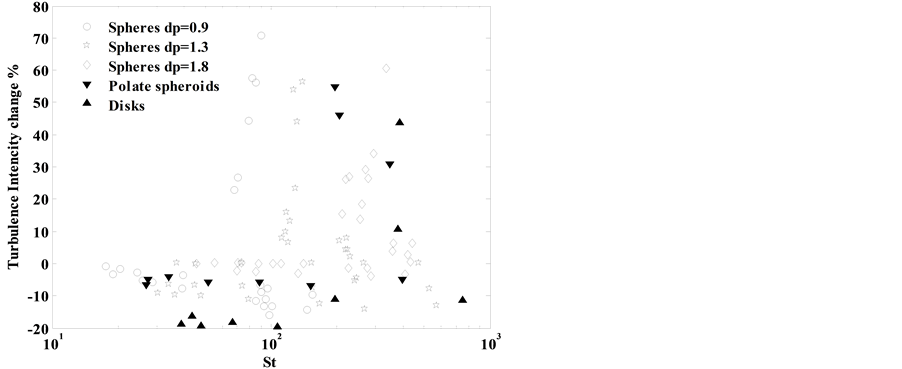
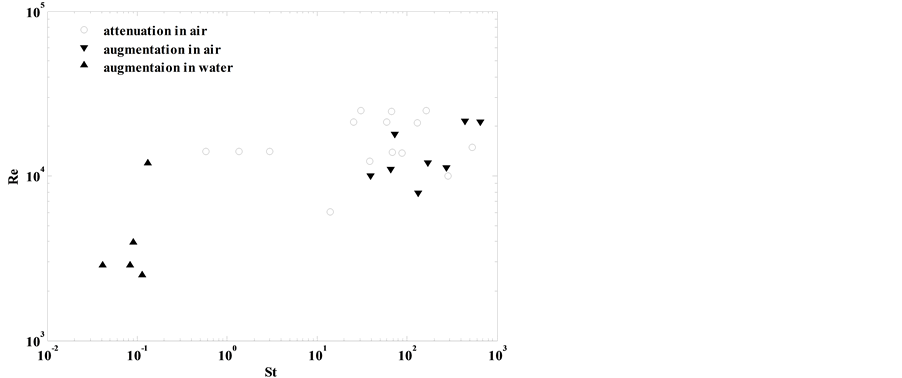
The particles will not be able to follow the motion of smaller eddies perfectly as their size increases and they will follow eddies of larger scale, more frequency [21] . Larger particles lead to increase in TKE, as detected by [22] . The reason to this may be vortex shedding behind the particle. For very high St or particles with diameter around the Taylor length scale, St cannot be used to describe the characteristics of the turbulent modification [23] -[25] . The particle relaxation time definition based on the analytical solution of Stokes equation for creeping flow (for particle falling from rest in stagnant fluid) can be safely applied to small particles of dp ~ η following the Kolmogorov theorem, Reη ~1. For larger particles inertia becomes important and the carrying phase has no obvious influence on the motion of the particles [26] . In this region, where inertia is significant, the assumptions, Reη ~1, for which relaxation time scales have been derived is no longer valid. Mandø [17] investigated particles with St = 10 - 1000. For 10 < St < 60, the turbulent intensity TI is attenuated or stay unchanged as shown in Figure 2. Increasing St over 60 may however result in as well amplification as attenuation of TI and notice that the attenuation can be substantial. Based on a review, Tanaka and Eaton [18] could not find any trend for turbulent modification that is independent on the fluid studied, as shown in Figure 3.
The discussion, so far, on St is based on the assumption of spherical particles. For non-spherical particles additional mechanism with coupled translational and rotational motion should be included. To exemplify, on top of
Figure 1. Classification map for St [19] .
Figure 2. Relation between TI and St for different particles [17] ; Note that particles size are in mm.
Figure 3. Turbulent modulation as function of St and Re for air and water [18] .
the translational relaxation time scale there is a rotational relaxation time scale that is strongly depend on the rotation axis of the particle making it rather difficult to define a single relaxation time [27] .
5. Particle Reynolds Number & Reynolds Number
Reynolds number
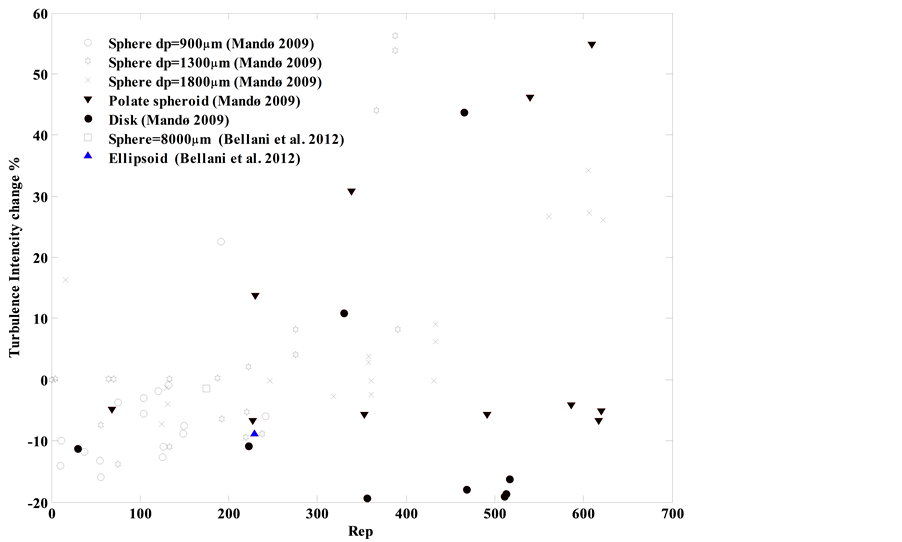
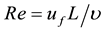 is the ratio of fluid inertia fluid viscosity and Rep can be identified as the ratio of inertia to viscosity in the fluid close to the surface of the particle. Rep decides the nature of the flow around a particle, the type of boundary layer around the particle (laminar or turbulent) and the occurrence of vortex shedding. In general, studies yield turbulent attenuation for low Rep and turbulent amplification for Rep ≥ 400 [28] . The latter may be explained with a transfer of some of the flow kinetic energy into turbulence through vortex shedding. Geiss [28] found significant turbulence production also for Rep less than 400. Mandø [17] measured in most cases a decrease in TI when adding spherical particles of Rep < 200 while for Rep > 400, nearly all measurements on spherical particles gave an amplification in TI, see Figure 4 where the variation in TI is plotted as a function of Rep for spherical and non-spherical particles. Mandø [17] , and the reference therein, argued that wake instability occurs at Rep ≈ 130 and vortex shedding start at Rep ≈ 270, which give the indication that the increase in TI could not be solely because of vortex shedding, otherwise, the lower critical value of vortex shedding formation Rep ≈ 270 would have been the value which distinguishes between increasing and decreasing in
is the ratio of fluid inertia fluid viscosity and Rep can be identified as the ratio of inertia to viscosity in the fluid close to the surface of the particle. Rep decides the nature of the flow around a particle, the type of boundary layer around the particle (laminar or turbulent) and the occurrence of vortex shedding. In general, studies yield turbulent attenuation for low Rep and turbulent amplification for Rep ≥ 400 [28] . The latter may be explained with a transfer of some of the flow kinetic energy into turbulence through vortex shedding. Geiss [28] found significant turbulence production also for Rep less than 400. Mandø [17] measured in most cases a decrease in TI when adding spherical particles of Rep < 200 while for Rep > 400, nearly all measurements on spherical particles gave an amplification in TI, see Figure 4 where the variation in TI is plotted as a function of Rep for spherical and non-spherical particles. Mandø [17] , and the reference therein, argued that wake instability occurs at Rep ≈ 130 and vortex shedding start at Rep ≈ 270, which give the indication that the increase in TI could not be solely because of vortex shedding, otherwise, the lower critical value of vortex shedding formation Rep ≈ 270 would have been the value which distinguishes between increasing and decreasing in
Figure 4. Alteration in TI as function of Rep when adding spherical and non-spherical.
turbulence. Non-spherical Rep is a function of the equivalent particle diameter and sphericity. The magnitude of vortex shedding now also becomes dependent on the rotation and orientation of the particle axis with respect to the mean flow direction.
In turbulent flow, length scales are affected by the turbulent Reynolds number Ret. Tanaka, Eaton [18] found that Reynolds number based on the integral length scale
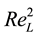 relates to the ratio of dp and η since ReL sets η. Reynolds number and the shape of the particles have a major influence on the secondary motion related to non-spherical particle. The particles may move in different ways like slow motion in orbits, translating with maximum cross-section aligned normal to the flow and large periodic swings around the mean path or chaotic tumbling [11] . All these motions will affect the interaction between the two phases.
relates to the ratio of dp and η since ReL sets η. Reynolds number and the shape of the particles have a major influence on the secondary motion related to non-spherical particle. The particles may move in different ways like slow motion in orbits, translating with maximum cross-section aligned normal to the flow and large periodic swings around the mean path or chaotic tumbling [11] . All these motions will affect the interaction between the two phases.
6. Length Scales
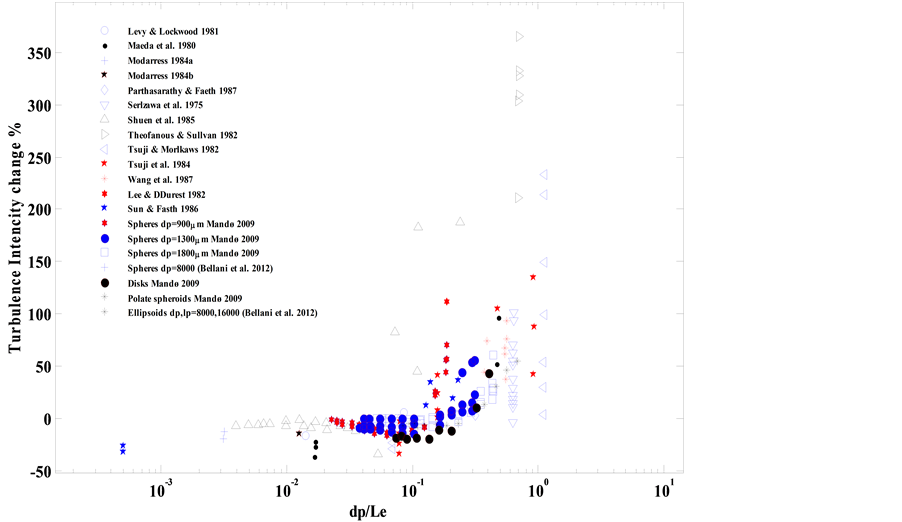
When particles with dp ~ η are added to the flow experiments yield that TKE decreases considerably as compared to a case without particles. This implies that dp/η is an important non-dimensional variable. However, Eaton [29] argued that most experimental works leading to this conclusion have been conducted with velocities in the range of 10 - 50 m/s and with a large length scale in the order of 10 - 50 mm. With the resulting rather narrow Re range it is not clear if it is correct to scale dp with. On the other hand, Eaton concluded that for dp ~ η turbulent eddies may be distorted by individual particles rather than be effected by a cloud of particles. The strong decrease in TKE is thus partly a reflection of local dissipation of turbulence around individual particles. Hwang and Eaton [30] examined isotropic turbulent with no mean flow in a tank with particles where dp ~ η and found attenuation in TKE of as much as 35% - 40%. Mandø [31] and Gore and Crowe [32] reported that it is better to use the ratio of dp to the characteristic length of the most energetic eddy, Le, of the single phase to scale the turbulent modulation. Poelma et al. [33] argued that Le and η have a fixed ratio so these length scales will play the same role. This conclusion was based on experiments with spherical particle in solid-gas, solid-liquid and gas-liquid turbulent upward and downward jet and pipe flow. Gore [32] analyzed about 15 studies in order to categorize the modification of the TI at the central region of the flow with usage of the dp/Le ratio. A critical value of dp/Le ≈ 0.1 was observed, as illustrated in Figure 5, and over this value the relative TI was considerably increased. Gore and Crowe [34] also summarized that with the range of parameters examined there was no large influence of adding particles on Le.
Figure 5. TI as function of dp/Le for spherical and non-spherical particles.
As shown in Figure 5, Mandø [17] found attenuation for dp/Le < 0.1 and only amplification for dp/Le > 0.3 for the range of parameters studied. Mandø [17] and references therein defined 200 μm as the critical diameter above which TI increases for a case with particles compared to one without. Small particles follow the dissipative scale eddies and there is momentum transfer from the carrier phase to the particles increasing energy dissipation and reducing the life time of the eddies In agreement with the results in Figure 4, Figure 5 results in [18] indicate that a variation in dp/Le has a large effect on the carrier-phase flow.
For non-spherical particles different definitions of the equivalent diameter have been presented and each of them will give different values so the application will decide which one is the most appropriate. To exemplify, [17] used the equivalent volume diameter while [35] used the diameter of the sphere that has the same average Stokesian response time as an ensemble of randomly oriented ellipsoids.
7. Particle Volume Fraction and Mass Loading
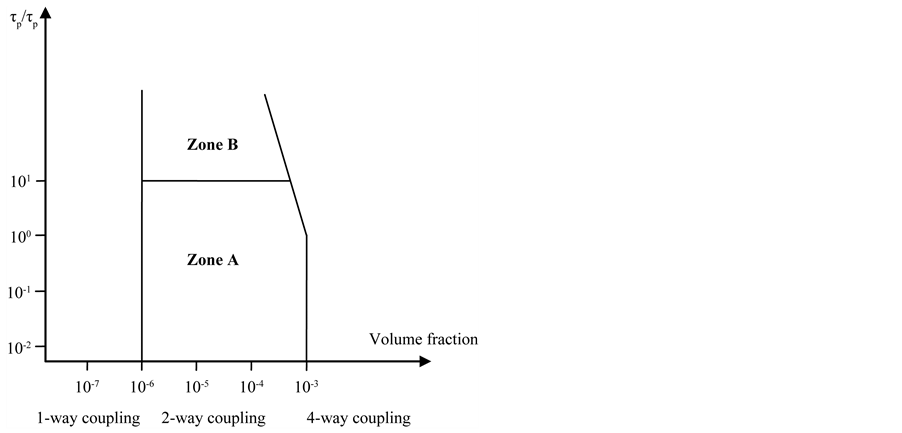
The volume fraction Φv may be defined as the volume occupied by the dispersed phase to the unit volume of the carrier phase in two phase flow, while, the mass loading Φm is defined as the ratio of dispersed to carrier phase mass flow rates. The intermediate volume loading fraction, which is defined by the lower and upper limits for two-way solid-gas interaction, is 10−6 < Φv < 10−3. For cases with Φv > 10−3 the particle-particle interaction will be important and the situation is denoted four way-coupling. If Φv < 10−6 the particles are few and there is a large distance between the particles which is referred to a one way coupling case, as shown in Figure 6. Notice that these limits are restricted to spherical particles and that the limits for respectively coupling is typically lower for non-spherical particles.
Some researchers argued that even with a very low Φv (lower than 10−6) there is change in turbulence of the carrier phase (two-way coupling) [36] [37] . Balachandar, Eaton [10] , Hwang and Eaton [30] and Wu et al. [36] (2006) show that there is generally attenuation of turbulence when adding particles and for small particles dp < η, the attenuation increased with increased Φm. It was concluded that turbulence modulation was observed even for very small Φv and Φm. For very small particles with very small Φv the turbulence is, however, generated almost as for single-phase flow.
Li [38] investigated a fully develop horizontal channel gas-solid flow with dp = 60 and 110 μm for small Φm. By a simultaneous two-phase PIV measurement technique they found a reduction in the relative mean velocity in the core region and increase of it in the near wall region when adding particles. It was also found an overall
Figure 6. Elgobashi et al. [17] classification map.
attenuation of turbulence, in the boundary layer and in the core region. Hence although turbulence is attenuated there is an increase in transport of momentum form the core to the boundaries. Li [39] used the same experimental set-up with simultaneous two-phase PIV high spatial resolution and a small interrogation window to enhance the accuracy. One result was that particle inertia changes the viscous sub-layer of the carrier fluid turbulence another result was a modification in turbulence with a very small Φm.
Tanaka [22] studied the microscopic particle-fluid interaction around particles with a high resolution PIV system. In general, there was attenuation of turbulence for the parameters studied with a maximum reduction of 25%. By using the two-point correlation it was found that the dissipation rate was significantly less altered as compared to the TKE. This finding was explained with two mechanisms. First, as the large scale turbulence attenuate there is less energy to be transferred to the smaller scales and less dissipation can be predicted. On the other hand, the particles were heavy, relative to the gas and owing to this, the particles themselves will produce vortices and amplify the rate of dissipation. Measurements near the particles show that the TKE attenuated because of the large density ratio, ≈ 10−3, so the particles behave like localized dampers for the turbulence, with strong energy dissipation around them. Hence the particles contribute to transport of the momentum as previously discussed.
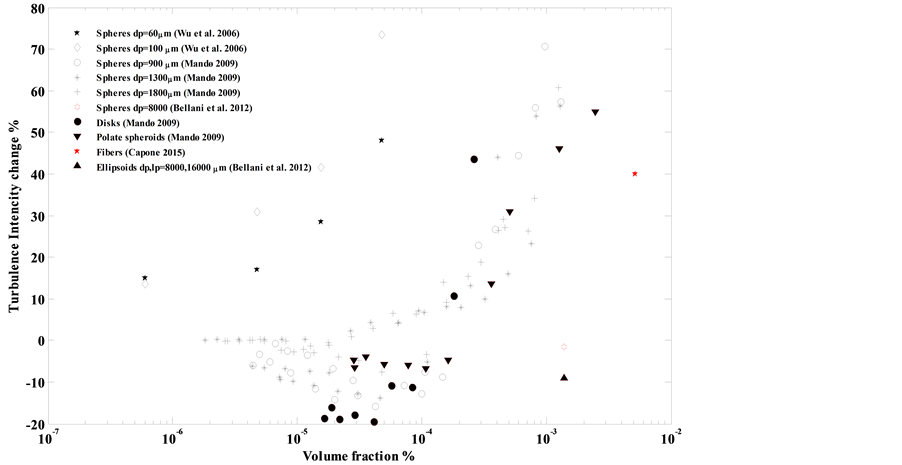
Other studies show small Φv has no influence on the carrier phase turbulence modulation, indicating that a one-way coupling approach is sufficient, [40] . Sad Chemloul [41] studied the effect of glass particles on water pipe flow with LDA and found a reduction in TI as a function of an increase in volume fraction particles. Mandø [17] investigated large particles in the form of spheres, disks, and prolate spheroids, in a vertical jet setup with a standard LDA system. Both attenuation and amplification was found for the St investigated. The author established a clear relation between turbulent modulation and Φv. Only amplification was observed for Φv > 2 × 10−4 while only attenuation was observed for Φv < 2 × 10−5. In agreement with [39] it was confirmed that Φv = 10−6 is a distinguishing limit between one-way and two-way coupling. Li [39] and Mandø [17] found more attenuation in turbulence when moving from spherical to non-spherical shaped particles (actually in conflict with [35] , see Figure 7 showing the relation between TI and volume fraction Φv as derived from the literature with spherical and non-spherical particles. Goswami [42] investigated a two-dimensional fully developed vertical solid-gas turbulent flow (1 m developing section, and length to width ratio = 25). At low Φv they found no significant effect from of the solid phase on the carrier phase.
It has been observed that the fractions Φm and/or Φv of non-spherical particles influence the flow. It has, for instance, been shown that the turbulence intensity increased in regions with increase in fiber volume concentration [16] . In the cases where qualitative effect was found, [31] for instance, it has been argued that this is a result of interactions with the length scale. This may be an evidence of that the mechanism of the carrier phase turbulent modulation takes place near the particle size scale or at least the important part of it.
Figure 7. Relationship between TI and volume fraction Φv.
8. Particle Momentum Number
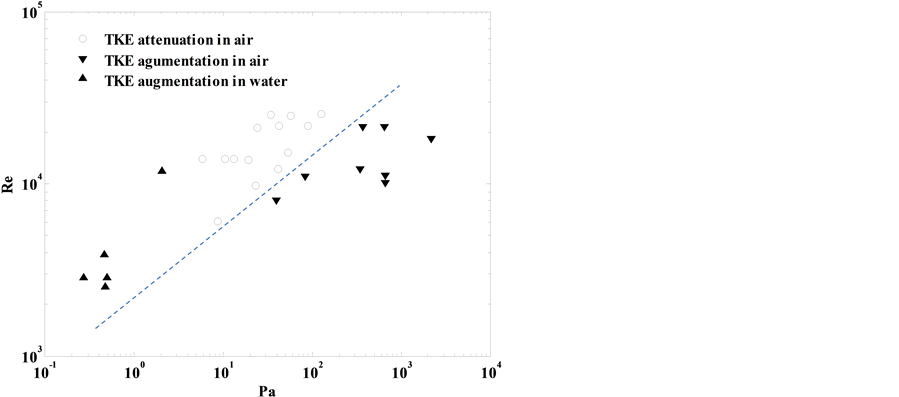
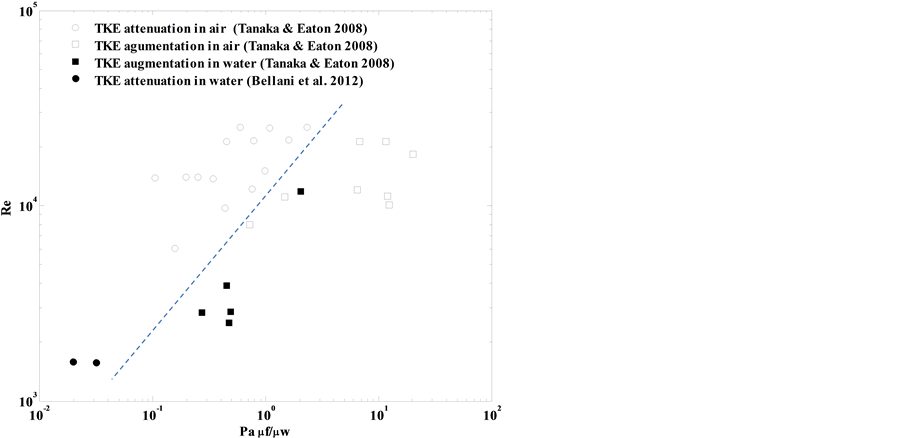
A relatively new dimensionless number, the Particle momentum number Pa, was proposed by [18] for the particle laden Navier-Stokes equation in order to classify results from the literatures into TKE amplification and at-
tenuation respectively. The definition is Pa = St Re2 (η/Le) which is equal to
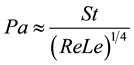 [43] . By plotting
[43] . By plotting
Pa as function of Tanaka and Eaton found that there was augmentation in TKE for Pa < 103 and attenuation for 103 < Pa < 105. Another area of augmentation was found after Pa = 105, as shown in Figure 8. As usually when dealing with St, Tanaka and Eaton derived the particle response time with the assumption of creeping flow which is valid for Re < 1. Lohse [43] had two viewpoints related to the non-monotonic behavior of TKE with Pa and the relation of Pa with St and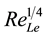
9. Conclusions
A critical review of the most important mechanisms and variables for the classification of turbulent modulation in the presence of spherical and non-spherical particles has been presented. At the moment there is no agreement in the scientific community on a single dimensionless number that can safely describe the influence of particles in turbulent flow. Hence, additional evaluations of turbulent modulation are required to estimate the interaction of several mechanisms at the level of single particles.
For non-spherical particles additional levels of freedom are introduced and the dependence on drag and lift from the orientation of the particles as and a function of Re adds to the complexity. Therefore, for non-spherical particles, the most convenient solution presently is to use length scales. Alternatively, Re and the response time describe phenomenon related to rotation, orientation and shape.
We showed that each of the important dimensionless numbers has their advantages and drawbacks and none of them covers all parameters relevant to turbulent modulation. The particle momentum number seems promising but need more analyzing and data especially for attenuation in water. Table 2 gives a summary for the
Figure 8. Particle momentum number Pa as function of Reynolds number ReLe.
Figure 9. Pa μf/μw as function of Reynolds number ReLe.
Table 2. Non-dimensional parameters range for turbulence modulation.
ranges of the parameters describe qualitatively the turbulent modulation.
Many studies was oriented toward introducing a particle source term based on the Euler/Lagrange approach that can account for the effect of spherical particles on the turbulence equations models regarding both augmentation and attenuation. No such source term has successfully been introduced for non-spherical particles.
The review demonstrates the need for more numerical and experimental work with higher accuracy than presented so far and the need to resolve the flow near the surface of particles with the aim to re-evaluate the quantitative effect of different parameters on turbulent modulation. It is very expensive to use the DNS method to resolve the flow of hundreds of particles and the use of LES with point force coupling is limited for small particles d ≤ η.
An interesting observation overall is that the particles may absorb a lot of turbulent energy at the same time as they themselves transport momentum from areas of high flow rate to areas of low flow rate.
Cite this paper
AmmarSaber,T. StaffanLundström,J. Gunnar I.Hellström, (2015) Turbulent Modulation in Particulate Flow: A Review of Critical Variables. Engineering,07,597-609. doi: 10.4236/eng.2015.710054
References
- 1. Goharzadeh, A., Rodgers, P. and Wang, L. (2013) Experimental Characterization of Slug Flow on Solid Particle Transport in a 1 Deg Upward Inclined Pipeline. Journal of Fluids Engineering, 135, Article ID: 081304.
http://dx.doi.org/10.1115/1.4024272 - 2. Misiulia, D., Andersson, A. and Lundström, T. (2015) Computational Investigation of an Industrial Cyclone Separator with Helical-Roof Inlet. Chemical Engineering & Technology, 38, 1425-1434.
http://onlinelibrary.wiley.com/doi/10.1002/ceat.201500181/epdf - 3. Johansson, S., Westerberg, L. and Lundström, T.S. (2014) Gas and Particle Flow in a Spray Roaster. Journal of Applied Fluid Mechanics, 7, 187-196.
- 4. Högberg, S.M., Akerstedt, H.O. and Holmstedt, E. (2012) Time-Dependent Deposition of Micro-and Nanofibers in Straight Model Airways. Journal of Fluids Engineering, 134, Article ID: 051208.
http://dx.doi.org/10.1115/1.4006698 - 5. Ljung, A., Frishfelds, V. and Lundström, T.S. (2012) Discrete and Continuous Modeling of Heat and Mass Transport in Drying of a Bed of Iron Ore Pellets. Drying Technology, 30, 760-773.
http://dx.doi.org/10.1080/07373937.2012.662567 - 6. Högberg, S. and Lundström, T. (2011) Motion of Dispersed Carbon Nanotubes during Impregnation of Fabrics. Plastics, Rubber and Composites, 40, 70-79.
http://dx.doi.org/10.1179/1743289811Y.0000000005 - 7. Ljung, A., Staffan Lundström, T. and Daniel Marjavaara, B. (2011) Convective Drying of an Individual Iron Ore pellet—Analysis with CFD. International Journal of Heat and Mass Transfer, 54, 3882-3890.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2011.04.040 - 8. Högberg, S.M., Åkerstedt, H.O. and Lundström, T.S. (2010) Respiratory Deposition of Fibers in the Non-Inertial Regime—Development and Application of a Semi-Analytical Model. Aerosol Science and Technology, 44, 847-860.
http://dx.doi.org/10.1080/02786826.2010.498455 - 9. Klett, J.D. (1995) Orientation Model for Particles in Turbulence. Journal of the Atmospheric Sciences, 52, 2276.
http://dx.doi.org/10.1175/1520-0469(1995)052<2276:OMFPIT>2.0.CO;2 - 10. Balachandar, S. and Eaton, J.K. (2010) Turbulent Dispersed Multiphase Flow. Annual Review of Fluid Mechanics, 42, 111-133.
- 11. Mandø, M. and Rosendahl, L. (2010) On the Motion of Non-Spherical Particles at High Reynolds Number. Powder Technology, 202, 1-13.
http://dx.doi.org/10.1016/j.powtec.2010.05.001 - 12. Crowe, C.C.T., Schwarzkopf, J.D. and Sommerfeld, M. (2011) Multiphase Flows with Droplets and Particles. CRC Press, Boca Raton.
http://dx.doi.org/10.1201/b11103 - 13. Patro, P. and Dash, S.K. (2014) Computations of Particle-Laden Turbulent Jet Flows Based on Eulerian Model. Journal of Fluids Engineering, 136, Article ID: 011301.
http://dx.doi.org/10.1115/1.4025364 - 14. Gore, R.A., Crowe, C.T. and Gore, R.A. (1991) Modulation of Turbulence by a Dispersed Phase. Journal of Fluids Engineering, 113, 304-307.
http://dx.doi.org/10.1115/1.2909497 - 15. Bellani, G., Nole, M.A. and Variano, E.A. (2013) Turbulence Modulation by Large Ellipsoidal Particles: Concentration Effects. Acta Mechanica, 224, 2291-2299.
http://dx.doi.org/10.1007/s00707-013-0925-z - 16. Capone, A., Romano, G.P. and Soldati, A. (2015) Experimental Investigation on Interactions among Fluid and Rod-Like Particles in a Turbulent Pipe Jet by Means of Particle Image Velocimetry. Experiments in Fluids, 56, 1-15.
- 17. Mandø, M. (2009) Turbulence Modulation by Non-Spherical Particles. Ph.D. Thesis, Department of Energy Technology, Aalborg University, Aalborg.
- 18. Tanaka, T. and Eaton, J.K. (2008) Classification of Turbulence Modification by Dispersed Spheres Using a Novel Dimensionless Number. Physical Review Letters, 101, Article ID: 114502.
http://dx.doi.org/10.1103/PhysRevLett.101.114502 - 19. Elgobashi, S., Balachandar, S. and Prosperetti, A. (2006) An Updated Classification Map of Particle-Laden Turbulent Flows. IUTAM Symposium on Computational Approaches to Multiphase Flow, 81, 3-10.
http://dx.doi.org/10.1007/1-4020-4977-3_1 - 20. Luo, K., Fan, J. and Cen, K. (2005) Modulations on Turbulent Characteristics by Dispersed Particles in Gas-Solid Jets. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 461, 3279-3295.
http://dx.doi.org/10.1098/rspa.2005.1517 - 21. Owen, P. (1969) Pneumatic Transport. Journal of Fluid Mechanics, 39, 407-432.
http://dx.doi.org/10.1017/S0022112069002242 - 22. Tanaka, T. and Eaton, J.K. (2010) Sub-Kolmogorov Resolution Partical Image Velocimetry Measurements of Particle-Laden Forced Turbulence. Journal of Fluid Mechanics, 643, 177-206.
http://dx.doi.org/10.1017/S0022112009992023 - 23. Semeraro, O., Bellani, G. and Lundell, F. (2012) Analysis of Time-Resolved PIV Measurements of a Confined Turbulent Jet Using POD and Koopman Modes. Experiments in Fluids, 53, 1203-1220.
http://dx.doi.org/10.1007/s00348-012-1354-9 - 24. Lucci, F., Ferrante, A. and Elghobashi, S. (2011) Is Stokes Number an Appropriate Indicator for Turbulence Modulation by Particles of Taylor-Length-Scale Size? Physics of Fluids, 23, Article ID: 025101.
http://dx.doi.org/10.1063/1.3553279 - 25. Hetsroni, G. (1989) Particles-Turbulence Interaction. International Journal of Multiphase Flow, 15, 735-746.
http://dx.doi.org/10.1016/0301-9322(89)90037-2 - 26. Meyer, D.W. (2012) Modelling of Turbulence Modulation in Particle- or Droplet-Laden Flows. Journal of Fluid Mechanics, 706, 251-273.
http://dx.doi.org/10.1017/jfm.2012.251 - 27. Bellani, G., Byron, M.L., Collignon, A.G., Meyer, C.R. and Variano, E.A. (2012) Shape Effects on Turbulent Modulation by Large Nearly Neutrally Buoyant Particles. Journal of Fluid Mechanics, 712, 41-60.
http://dx.doi.org/10.1017/jfm.2012.393 - 28. Geiss, S., Dreizler, A. and Stojanovic, Z. (2004) Investigation of Turbulence Modification in a Non-Reactive Two-Phase Flow. Experiments in Fluids, 36, 344-354.
http://dx.doi.org/10.1007/s00348-003-0729-3 - 29. Eaton, J.K. (2009) Two-Way Coupled Turbulence Simulations of Gas-Particle Flows Using Point-Particle Tracking. International Journal of Multiphase Flow, 35, 792-800.
http://dx.doi.org/10.1016/j.ijmultiphaseflow.2009.02.009 - 30. Hwang, W. and Eaton, J.K. (2006) Homogeneous and Isotropic Turbulence Modulation by Small Heavy (St 50) Particles. Journal of Fluid Mechanics, 564, 361-393.
http://dx.doi.org/10.1017/S0022112006001431 - 31. Mand?, M., Lightstone, M.F., Rosendahl, L., Yin, C. and S?rensen, H. (2009) Turbulence Modulation in Dilute Particle-Laden Flow. International Journal of Heat and Fluid Flow, 30, 331-338.
http://dx.doi.org/10.1016/j.ijheatfluidflow.2008.12.005� - 32. Gore, R.A. and Crowe, C.T. (1989) Effect of Particle Size on Modulating Turbulent Intensity. International Journal of Multiphase Flow, 15, 279-285.
http://dx.doi.org/10.1016/0301-9322(89)90076-1 - 33. Poelma, C., Westerweel, J. and Ooms, G. (2007) Particle-Fluid Interactions in Grid-Generated Turbulence. Journal of Fluid Mechanics, 589, 315-351.
http://dx.doi.org/10.1017/S0022112007007793 - 34. Gore, R.A. and Crowe, C.T. (1991) Modulation of Turbulence by a Dispersed Phase. Journal of Fluids Engineering, 113, 304-307.
http://dx.doi.org/10.1115/1.2909497 - 35. Bellani, G. and Variano, E.A. (2012) Slip Velocity of Large Neutrally Buoyant Particles in Turbulent Flows. New Journal of Physics, 14, Article ID: 125009.
http://dx.doi.org/10.1088/1367-2630/14/12/125009 - 36. Wu, Y., Wang, H.F., Liu, Z.H., Li, J., Zhang, L.Q. and Zheng, C.G. (2006) Experimental Investigation on Turbulence Modification in a Horizontal Channel Flow at Relatively Low Mass Loading. Acta Mechanica Sinica, 22, 99-108.
http://dx.doi.org/10.1007/s10409-006-0103-9 - 37. Guo, F.-S., Wang, H.-F., Liu, Z.-H. and Zheng, C.-G. (2004) Experimental Investigations on Turbulence Modulation in a Horizontal Channel Flow Using PTV. Journal of Engineering Thermophysics, 25, 622-624.
- 38. Li, J., Wang, H.F., Liu, Z.H., Liu, Y.M., Han, H.F. and Zheng, C.G. (2010) Experimental Investigation on Turbulence Modulation in the Boundary Layer of a Horizontal Particle-Laden Channel Flow with Relative Low Mass Loading Ratios. The 6th International Symposium on Multiphase Flow, Heat Mass Transfer and Energy Conversion, 1207, 436-441.
http://dx.doi.org/10.1063/1.3366404 - 39. Li, J., Wang, H.F., Liu, Z.H., Chen, S. and Zheng, C.G. (2012) An Experimental Study on Turbulence Modification in the Near-Wall Boundary Layer of a Dilute Gas-Particle Channel Flow. Experiments in Fluids, 53, 1385-1403.
http://dx.doi.org/10.1007/s00348-012-1364-7 - 40. Graham, D.I. (2000) Turbulence Attenuation by Small Particles in Simple Shear Flows. Journal of Fluids Engineering, 122, 134-137.
http://dx.doi.org/10.1115/1.483235 - 41. Sad Chemloul, N. and Benrabah, O. (2008) Measurement of Velocities in Two-Phase Flow by Laser Velocimetry: Interaction between Solid Particles’ Motion and Turbulence. Journal of Fluids Engineering, 130, Article ID: 071301.
http://dx.doi.org/10.1115/1.2948358 - 42. Goswami, P.S. and Kumaran, V. (2011) Particle Dynamics in the Channel Flow of a Turbulent Particle-Gas Suspension at High Stokes Number. Part 2. Comparison of Fluctuating Force Simulations and Experiments. Journal of Fluid Mechanics, 687, 41-71.
http://dx.doi.org/10.1017/jfm.2011.295 - 43. Lohse, D. (2008) Viewpoint: Particles Go with the Flow. Physics, 1, 18.
- 44. Knowles, P.L. and Kiger, K.T. (2012) Quantification of Dispersed Phase Concentration Using Light Sheet Imaging Methods. Experiments in Fluids, 52, 697-708.
http://dx.doi.org/10.1007/s00348-011-1100-8 - 45. Lu, Y., Glass, D.H. and Easson, W.J. (2009) An Investigation of Particle Behavior in Gas-Solid Horizontal Pipe Flow by an Extended LDA Technique. Fuel, 88, 2520-2531.
http://dx.doi.org/10.1016/j.fuel.2009.02.038 - 46. Zhou, Q. and Cheng, N.-S. (2009) Experimental Investigation of Single Particle Settling in Turbulence Generated by Oscillating Grid. Chemical Engineering Journal, 149, 289-300.
http://dx.doi.org/10.1016/j.cej.2008.11.004 - 47. Mathisen, A., Halvorsen, B. and Melaaen, M. (2008) Experimental Studies of Dilute Vertical Pneumatic Transport. Particulate Science and Technology, 26, 235-246.
http://dx.doi.org/10.1080/02726350802028900 - 48. Zhang, Y., Lim, E.W.C. and Wang, C.H. (2007) Pneumatic Transport of Granular Materials in an Inclined Conveying Pipe: Comparison of Computational Fluid Dynamics-Discrete Element Method (CFD-DEM), Electrical Capacitance Tomography (ECT), and Particle Image Velocimetry (PIV) Results. Industrial & Engineering Chemistry Research, 46, 6066-6083.
http://dx.doi.org/10.1021/ie061304i - 49. Laín, S. and Sommerfeld, M. (2007) A Study of the Pneumatic Conveying of Non-Spherical Particles in a Turbulent Horizontal Channel Flow. Brazilian Journal of Chemical Engineering, 24, 535-546.
http://dx.doi.org/10.1590/S0104-66322007000400007 - 50. Ljus, C., Johansson, B. and Almstedt, A.-E. (2002) Turbulence Modification by Particles in a Horizontal Pipe Flow. International Journal of Multiphase Flow, 28, 1075-1090.
http://dx.doi.org/10.1016/S0301-9322(02)00020-4 - 51. La??n, S., Sommerfeld, M. and Kussin, J. (2002) Experimental Studies and Modelling of Four-Way Coupling in Particle-Laden Horizontal Channel Flow. International Journal of Heat and Fluid Flow, 23, 647-656.
http://dx.doi.org/10.1016/S0142-727X(02)00160-1� - 52. Kiger, K.T. and Pan, C. (2002) Suspension and Turbulence Modification Effects of Solid Particulates on a Horizontal Turbulent Channel Flow. Journal of Turbulence, 3, N19.
http://dx.doi.org/10.1088/1468-5248/3/1/019