Received 8 June 2015; accepted 15 June 2015; published 30 June 2015

ABSTRACT

As part of a research intending to develop steel-concrete hybrid girder using ultra high performance concrete with compressive strength of 80 MPa, this study conducts loading test on this girder to investigate the methods for its composition with a slab using 30 MPa-concrete and the corresponding interfacial behavior. Prior to the loading test, the design formula of the Eurocode for the shear resistance developed in concrete-to-concrete interface is examined for the interface between concrete layers of different strengths. The effect of the surface roughness on the shear resistance is examined using this formula and finite element analysis to verify the applicability of the formula. Based upon the results, loading test is conducted on girder specimens to evaluate the actual behavior with respect to the interfacial surface condition. The test results reveal that the specimen with rough interface could not develop perfectly composite behavior and experienced adhesive failure. In case of simultaneous action of flexure and shear, it appears that conservative design should be applied without consideration of the interfacial condition when determining the arrangement of shear reinforcement.

Keywords:

Shear Resistance, Interface between Concrete Layers, Surface Roughness, Steel-Concrete Hybrid Girder, Ultra High Performance Concrete (UHPC)

1. Introduction

The transfer mechanism of the shear stress developed in a member combining concrete layers with different strengths is very complicated. This mechanism is subordinate to the effect of various parameters like the amount of reinforcing steel traversing the interface, the compressive resistance of the lower strength concrete, the degree of roughness of the interface, and the stress provoked by the vertical load. Research on this mechanism started in 1960s like the works of Hanson [1] , Birkeland and Birkeland [2] , Mattock and Hawkins [3] , Walraven and Reinhardt [4] and, Loov and Patrnaik [5] who conducted diverse research on the shear frictional behavior. Recently, Júlio and Santos [6] [7] established an acknowledged theory explaining the transfer mechanism of the shear stress occurring at the interface between concrete layers. These authors explained that the shear resistance at the concrete-to-concrete interface is developed through the combination of the adhesive bond caused by the separated placing of the layers, the dowel action of the reinforcing steel, and the friction occurring after the initiation of cracks at the interface [1] . The design specification of Eurocode [8] refers to this theory.

This study proposes the hybrid girder shown in Figure 1 composing a casing made of 80 MPa-ultra high performance concrete (UHPC) with the upper flange made of 30 MPa-concrete in order to reduce the depth of the steel composite girder.

The design formula for the shear resistance suggested in Eurocode is applied to determine the amount of shear reinforcement for the composition between the casing and the slab. However, this formula does not consider the strength difference between the concrete layers. Therefore, its applicability is verified by comparing the shear resistance provided by the formula and that obtained through finite element analysis performed considering the interface between concretes of different strengths. Moreover, the amount of steel reinforcement for shear composition is determined using the design formula of Eurocode and adopted to fabricate the girder specimens of which behaviors are compared with respect to the surface roughness of the interface.

2. Verification of Applicability of Eurocode Design Formula by Finite Element Analysis

2.1. Eurocode Design Formula for Shear Resistance

The design formula for the shear resistance at the interface of concretes placed at different times suggested by Eurocode [8] is expressed in Equation (1) using 3 resistance terms.

(1)

where cf_ctd = adhesion resistance between materials at interface that is determined with respect to the design tensile strength of concrete (f_ctd); μσ_n = shear friction resistance caused by the normal stress (σ_n) due to external load and that is determined with respect to the surface roughness (μ); and, ρf_syd (μsinα + cosα) = shear resistance by shear reinforcement that is determined with respect to the reinforcement ratio (ρ), the yield strength of reinforcement (f_syd), and the surface roughness (μ). Here, the values of the factors c and μ related to the interfacial roughness are given in Table 1.

Equation (1) calculates the shear strength at the interface between members of same strength but placed at different times. It is thus necessary to verify its applicability to the case of members with different strengths. Therefore, the results provided by the design formula and finite element analysis are compared.

2.2. Evaluation of Interface Shear Resistance Formula by Finite Element Analysis

Figure 2 presents the model describing the surface roughness by means of indented construction joint. Figure 3 illustrates the finite element model simulating the surface condition at the interface between concrete layers.

Two heights (d) of 6 mm and 10 mm are chosen for the indent, and analysis is also performed for the smooth surface without irregularities (d = 0 mm). Two models are considered: model SC80-NC30 in which the strength of the lower concrete layer is 80 MPa and that of the upper concrete layer is 30 MPa, and model NC30-NC30 applying the same strength of 30 MPa for both upper and lower concrete layers. The vertical load is applied in the form of an uniformly distributed load of 2.5 kN/m. The analysis is conducted through displacement control in which the upper layer moves horizontally and the lower layer is fixed.

Equation (2) expresses the stress-strain relation of concrete adopted in the analysis and is the one proposed by fib Model Code [9] . The characteristics values arranged in Table 2 are applied in Equation (2) to assume the curves plotted in Figure 4.

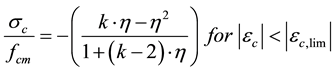(2)

where with ε_cl = strain at maximum compressive stress; and, k = plasticity number = 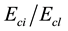with E_cl = secant modulus from the origin to the peak compressive stress.

Figure 5 compares the shear resistance obtained by the analysis and the design formula in Equation (1). In Figure 5(a) comparing the results for smooth surface interface, the analytic result for model NC30-NC30 is seen to be approximately 1.3 times larger than that given by the design formula and, to be about 1.4 times larger for model SC80-NC30. Here, the design value for model SC80-NC30 was calculated assuming concrete strength of 80 MPa for both layers. For the indented surface in Figure 5(b), the variation in the shear resistance obtained analytically remains below 5% according to the indent depth d. If the depth is larger than 5 mm as shown in Figure 2, the shear strength obtained by means of the shape of the indent converges to a definite level. With regard to the model with indented surface, the analytical results are seen to be approximately 1.3 times larger than those calculated by the design formula.

In view of these observations, in case of concrete layers with different strengths, a conservative design value with safety factor of about 1.6 is computed when the shear resistance is calculated by adopting the physical properties of the material with lower strength in the design formula for shear resistance.

3. Loading Test of Girder for Shear Resistance Evaluation with Respect to Interface Condition

Loading test is performed on girder specimens fabricated considering the inter-layer surface condition as variable in order to evaluate the ultimate load and behavior of the composite section with respect to the design method applied for the shear resistance at the interface between concrete layers. As shown in Figure 6, the compressive strength of the concrete casing is 80 MPa and that of the concrete slab is 30 MPa. The composition of the steel girder and concrete casing is realized by means of headed studs, and the composition of the concrete

casing and slab is designed using shear reinforcement. The length of the girder is 8 m and loading is applied at the center of the girder.

Three types of girder specimens are considered according to the design condition between the concrete casing and slab. Table 3 arranges the interface design results per type of specimen. Here, SC1 designates the specimens without surface treatment and for which the arrangement of shear reinforcement has been designed, SC2 stands for the specimens in which the spacing of shear reinforcement is enlarged considering the shear resistance brought by the interlocking effect of the indents with depth of 6 mm, width of 40 mm, and spacing of 40 mm. SC3 indicates the specimens with surface treatment corresponding to the rough condition in Table 1 and in which spacing of shear reinforcement is enlarged considering the interlocking effect. The ultimate load by plastic design is 2273 kN for all the specimens.

Figure 7 plots the load-displacement curves per type of specimen obtained by loading test, and Table 4 lists the measured peak load. In case of SC2 specimen, after the tensile stress in bottom flange of steel girder reached to the yield stress, the specimen abruptly failed by the shear failure in the layer interface. SC3 specimen also failed by the shear failure in the layer interface while it didn’t show the abrupt failure.

For the failure mode, SC1 failed through compression of the slab of its deck, and SC2 and SC3 underwent

^aComposition of steel girder and concrete casing; ^bComposition of concrete casing and slab.

shear failure of the interface between the concrete casing and slab. Particularly, specimen SC2 with surface treatment by means of 6 mm-deep indents experienced sudden failure of the interfacial indents during the loading process.

For the peak load, only specimen SC1 showed a peak load increased by 6% compared to the design load whereas specimens SC2 and SC3 failed at loads lower by 6% to 8% than the design load due to shear failure at the inter-concrete interface.

Figure 8 plots the strain distribution at yield load and peak load inside the central cross-section. For SC1, the strain distribution is linear until the peak load, which indicates that the specimen develops perfectly composite behavior. Whereas, for SC2 and SC3, the strain distribution shows the discontinuity and snapping point at the location of concrete casing and slab (at height of 275 mm), and it means the shear bond failure in the layer interface.

4. Conclusions

This study investigated the applicability of the design formula for shear resistance in concrete-to-concrete interface suggested in Eurocode to the case composing concrete layers with two different compressive strengths of 80 MPa and 30 MPa. To that goal, finite element analysis was performed to examine the effect of the surface condition of concrete on the shear strength. The results showed that, in case of concrete layers with different strengths, a conservative design value with safety factor of about 1.6 compared to the analytical value can be obtained when the shear resistance is calculated by adopting the lower strength in the design formula for shear resistance.

Based on such observation, the interfacial behavior and ultimate load were evaluated on hybrid girder specimens composing members of different strengths and fabricated considering the interface condition as variable. Referring to the specimen with smooth interface, the shear reinforcement for the composition of the specimens was designed so as to reduce the amount of reinforcement through the enlargement of the reinforcement spacing considering the shear resistance provided by the interlocking effect of the rough surface condition and indent condition at the interface. However, the loading test revealed that the actual ultimate load occurred at values lower by approximately 2% to 8% than the interface failure design load and that perfectly composite behavior could not be achieved. This could be explained by the fact that the design formula for shear resistance suggested in the design code is effective under the action of pure shear but fails to provide appropriate value for the interfacial shear resistance under the combined action of flexure and shear. It appears that conservative design shall be conducted by applying partial safety factor.

Acknowledgements

This study was supported financially through the project “Development of SUPER Concrete with compressive strength of 80 - 180 MPa and its application (2nd year)”. The authors express their gratitude for the support.

Cite this paper

Jae YoonKang,Jong SupPark,Woo TaiJung,Moon SeoungKeum, (2015) Connection between Concrete Layers with Different Strengths. Engineering,07,365-372. doi: 10.4236/eng.2015.77032

References

NOTES

^*Corresponding author.