Engineering
Vol.07 No.06(2015), Article ID:57196,9 pages
10.4236/eng.2015.76026
Microwave Heating of Liquid Foods
Vittorio Romano*, Rino Apicella
Dipartimento di Ingegneria Industriale, Università degli Studi di Salerno, Fisciano, Italy
Email: *vromano@unisa.it
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 November 2014; accepted 14 June 2015; published 17 June 2015
ABSTRACT
A mathematical model has been formulated to describe the heat transfer in liquid foods flowing in circular ducts, subjected to microwave irradiations. Three types of liquids with different rheological behavior are considered: skim milk (Newtonian), apple sauce and tomato sauce as non-New- tonian fluids. Each one can flow with different velocities but always in laminar way. The temperature profiles have been obtained solving the transient momentum and heat equations by numerical resolution using the Finite Element Method. The generation term due to the microwave heating has been evaluated according to Lambert’s law. Dielectric properties are considered to be temperature dependent.
Keywords:
Continuous Microwave Heating, Lambert’s Law, Non-Newtonian Fluids, FEM

1. Introduction
Microwave heating has been utilized since the 1940s [1] in different fields such as polymer and ceramics industries [2] [3] and medicine [4] [5] . However, food processing is the largest consumer of microwave energy, that can be employed for cooking, thawing, tempering, drying, freeze drying, pasteurization, sterilization, baking, heating and re-heating. In microwave heating, electromagnetic field polarizes the molecules of dielectric materials and creates dipole moments that cause these molecules to rotate. The resulting molecular friction causes heat generation in the body. Due to intrinsic heat generation capability, microwave heating can provide prompt rise of temperature within the low thermal conductive products, especially in food items. However, this technique is blamed for uneven heating since the food product processed with microwaves shows alternate hot and cold spots. This is primarily caused by the non-uniform distribution of microwave energy in the foodstuff, due to factors such as dielectric loss, penetration depth, thickness, shape and size of the sample.
Microwave heating of solid foods has been largely investigated in the last years. The energy equation is written as a conductive heat transfer with a generation term. The latter has been modeled by many authors, using two different approaches to evaluate the effects of the microwave distribution: by solving the Maxwell’s equations [2] [6] [7] or by applying the Lambert’s law [8] [9] . The Lambert’s law is a simple power formulation that was believed to simulate temperature profiles for Cartesian geometries and for cylindrical geometries with high radius. Ayappa et al. [2] deduced the minimum value of the characteristic sample dimension to successfully apply the law for slabs; Oliveira and Franca [7] found that this value was higher for cylinders than for slabs. Finally, Romano et al. [10] correctly applied Lambert’s law considering the geometry of the sample, thus finding the same field of application for both the shapes and a power concentration along the central axis for a cylindrical domain, according with the experimental observations [9] .
As regards fluids, there are fewer studies and the most are about batch processes [11] [12] . The references in continuous processes instead are represented by Salvi et al. [13] and J. Zhu et al. [15] whose mathematical model considers the generation term according to Maxwell’s equations. In this paper, Lambert’s law has been applied, that is much less expensive in terms of time of calculus. The aim is to verify whether similar results are obtained or not.
2. Mathematical Model
2.1. Physical System
The physical system represented in Figure 1 is a cylindrical horizontal tube with a length L = 0.3 m and a radius R = 0.02 m in which different liquid foods are heated by microwave irradiance in the radial direction.
A laminar flow at various velocities is realized by changing the difference of pressure between the inlet and the outlet sections. Only the axial component of the velocity is different from zero and it is a function of the variable r: vz = vz(r). The temperature, even though the microwave penetration is only radial, is also function of the axial direction z by the effect of the flow field: T = T(r, z).
2.2. Transport Equations
In order to find the temperature profile, the following mathematical model has been constructed.
It consists of the following three differential equations in cylindrical coordinate system with their boundary conditions [14]
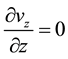 (Equation of continuity)
(Equation of continuity)
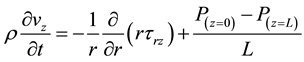 (Equation of motion)
(Equation of motion)
As initial condition, the fluid is stationary.
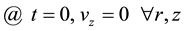 (1)
(1)
As boundary conditions, no slipping at the wall has been assumed
Figure 1. Representation of the cylindrical duct.
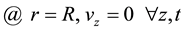 (2)
(2)
and symmetry on the axis has been considered.
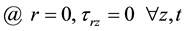 (3)
(3)
 (Energy equation)
(Energy equation)
As initial condition, the temperature of the fluid is assumed to be uniform
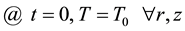 (4)
(4)
As boundary conditions for the radial direction, symmetry respect to the axis and heat convective flux at the wall have been considered.
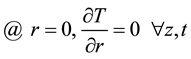 (5)
(5)
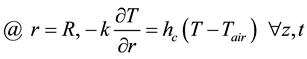 (6)
(6)
while for the z direction uniform temperature in the inlet section and Danckwerts condition in the outlet one have been imposed.
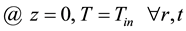 (7)
(7)
 (8)
(8)
Initial temperature T0 and input temperature Tin are both equal to environmental temperature Tair .
Heat generation due to microwaves has been modeled according to the Lambert’s law along the radial direction of a cylindrical sample [10] :
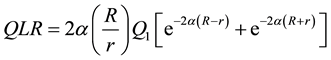
where
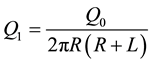

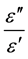 is the loss tangent, tanδ.
is the loss tangent, tanδ.
The attenuation factor for each fluid has been considered as a function of temperature, calculated by interpolation starting from graphic relationships for dielectric constant and loss tangent versus temperature in a range 10˚C - 90˚C [15] .
Such a system, with the equations and boundary conditions written before, results to be axial-symmetric.
3. Materials and Methods
To solve the previous partial differential equations, a Finite Elements Method (FEM) has been used. To practically implement this solution, COMSOL Multiphysics® has been utilized with the following mesh features: 2049 mesh points, 3840 triangular elements, 256 boundary elements and 4 vertex elements.
Figure 2 shows an example of mesh that the software uses to discretize the domain.
Three fluid foods have been considered: skim milk, with a Newtonian behavior (constant viscosity), apple sauce and tomato sauce as non Newtonian fluids, modeled with a power law having different fluid consistency coefficient and flow behavior index. All the physical properties of the three fluids are resumed in Table 1.
As ε' and ε" are temperature functions, average values have been obtained by integrating in the entire domain and in the time (range 0 - 50 s). They are fundamental for microwave heating, because they determine respectively the energy absorbed and the fraction converted in heat power.
4. Results
It is possible to make a qualitative analysis of the results observing the following temperature maps reported in Figures 3-5. They have been obtained with an incident power Q1 = 20,000 W・m−2, for each fluid, for two different velocities (2 mm/s and 4 mm/s) and for two different instants of time (30 s and 50 s). They show the temperature profiles in a rz plane section of the real physical system on the left and in a 3D plot on the right. The higher heating is obtained for longer times and lower velocities. The nature of liquid also have a great influence: skim milk reaches higher temperature with a less uniform profile.
The graphs in Figures 6-8 provide a more significant analysis since they show the temperature profiles along the radial direction, obtained with the same incident power of 20,000 W・m−2 and appointing the outlet section instead of the instant of time. In this way, each fluid element has the residence time due to its velocity, which is related to its position.
Figure 2. Example of a generic mesh.
Table 1. Physical, dielectric and transport properties (Zhu et al., 2007).
Figure 3. Temperature maps for skim milk, with vm = 2 mm/s (on the top) and vm = 4 mm/s (on the bottom).
In these graphs all the fluids show a minimum (cold spot) located at about half the radium. This is the sum of two effects: Lambert’s law that predicts a different heating along the radial direction and the flow field that produces different residence times inside the tube. In particular, near the axis (r = 0) the velocity is higher and so the residence times are lower, but according to the Lambert’s law, the power density is maximum by effect of the term R/r; conversely, near the wall (r = R) the velocity is lower and the times of exposition to the microwaves are higher, but the Lambert’s power density undergoes the effect of the exponential decay. These are opposite effects and their combination produces the previous profiles, with higher temperatures on the axis and on the wall.
The kind of fluid plays an important role, both for the rheological behavior and the dielectric properties, while the physical properties are quite the same for all of them. On one hand, pseudo plastics having a flatter velocity profile than Newtonian fluids, can’t fully balance the effect of Lambert’s law. On the other hand, the dielectric properties, in particular dielectric loss, determinant for the absorbed heat, are different fluid by fluid. Such dielectric properties cause a lower difference in the absorbed heat between axis and wall in the case of tomato sauce, as it can be noticed in Table 2.
As the ε' is quite the same for all the fluids, they absorb about the same quantity of energy from microwaves, but tomato sauce transforms the higher fraction of this energy into heat (Qconverted) by a higher value of ε'' and so it shows a higher average temperature. These results are resumed in Table 3.
Figure 4. Temperature maps for apple sauce, with vm = 2 mm/s (on the top) and vm = 4 mm/s (on the bottom).
5. Conclusions
In this paper, microwave heating of three liquid foods moving in a cylindrical duct with a laminar flow has been analyzed.
The multiphysics mathematical model considers the momentum and energy transport at unsteady state.
The analysis has been achieved with the Finite Element Method solving the mathematical model with Comsol®3.5.
Contrasting effects of Lambert’s law for microwave heating in case of a cylindrical geometry and distribution of residence times of the fluids in the duct have been taken into account.
Different factors play a role in case of microwave heating of a liquid. In particular, rheological and dielectric properties of the fluids have been considered and two different operational conditions have been obtained by varying the average velocity of the fluids.
Results show that absorbed power has always a maximum on the axis, caused by the ratio R/r appearing in the radial contribution to the microwave heat source for a cylindrical geometry; however, near the wall of the tube a high quantity of absorbed heat has been found, in this case due to the long times of residence of the fluid inside the tube.
Figure 5. Temperature maps for tomato sauce, with vm = 2 mm/s (on the top) and vm = 4 mm/s (on the bottom).
Figure 6. Temperature profiles for skim milk, Q1 = 20,000 W/m2.
Figure 7. Temperature profiles for apple sauce, Q1 = 20,000 W/m2.
Figure 8. Temperature profiles for tomato sauce, Q1 = 20,000 W/m2.
Table 2. Power density at axis and wall.
Table 3. Average over space and time of power density and temperature.
The final result is a double pick of absorbed heat on the axis and on the wall; between the two opposite effects the term R/r overcomes the one due to the residence time.
In any case, the absorbed powers are almost equal for the three fluids because the dielectric constants ε' are of the same order of magnitude, whereas the fraction of this energy which is dissipated into heat is different in the three cases as the dielectric losses ε" are different.
The tomato sauce gives the higher average temperature and also the more uniform temperature distribution.
We have compared these results with those obtained studying a cylindrical system with anon-symmetric microwaves exposure [15] in which Maxwell equations are used to evaluate the electromagnetic field. The temperature profiles are analogous even if obtained with different computational times: 50 hours with a 3.0 GHz processor using Maxwell equations, few minutes with a 2.1 GHz processor adopting Lambert’s law.
In both the cases, the temperature is higher on the axis, it decreases until about half the radius and it increases again near the wall. Furthermore, the lower difference between the hot and the cold spot in the temperature profile can be found in the tomato sauce case.
References
- Mermelstein, N.H. (1997) How Food Technology Covered Microwaves over the Years. Food Technology, 51, 82-84.
- Ayappa, K.G., Davis, H.T., Davis, E.A. and Gordon, J. (1991) Analysis of Microwave Heating of Materials with Temperature Dependent Properties. AIChE Journal, 37, 313-322. http://dx.doi.org/10.1002/aic.690370302
- Chatterjee, A., Basak, T. and Ayappa, K.G. (1998) Analysis of Microwave Sintering of Ceramics. AIChE Journal, 44, 10.
- O’Brien, K.T. and Mekkaoui, A.M. (1993) Numerical Simulation of the Thermal Fields Occurring in the Treatment of Malignant Tumors by Local Hyperthermia. Journal of Biomechanical Engineering, 115, 247-253. http://dx.doi.org/10.1115/1.2895482
- Paulsen, K.D., Lynch, D.R. and Strohbehn, J.W. (1998) Three-Dimensional Finite, Boundary, and Hybrid Element Solutions of the Maxwell Equations for Lossy Dielectric Media. IEEE Transactions on Microwave Theory and Techniques, 36, 682-693.
- Ayappa, K.G., Davis, H.T., Davis, E.A. and Gordon, J. (1992) Two Dimensional Finite Elements Analysis of Microwave Heating. AIChE Journal, 38, 1577-1592. http://dx.doi.org/10.1002/aic.690381009
- Oliveira, M.E.C. and Franca, A.S. (2002) Microwave Heating of Foodstuffs. Journal of Food Engineering, 53, 347- 359. http://dx.doi.org/10.1016/S0260-8774(01)00176-5
- Lin, Y.E., Anantheswaran, R.C. and Puri, V.M. (1995) Finite Element Analysis of Microwave Heating of Solid Foods. Journal of Food Engineering, 25, 85-112. http://dx.doi.org/10.1016/0260-8774(94)00008-W
- Zhou, L., Puri, V.M., Anantheswaran, R.C. and Yeh, G. (1995) Finite Element Modeling of Heat and Mass Transfer in Food Materials during Microwave Heating-Model Development and Validation. Journal of Food Engineering, 25, 509-529. http://dx.doi.org/10.1016/0260-8774(94)00032-5
- Romano, V.R., Marra, F. and Tammaro, U. (2005) Modelling of Microwave Heating of Foodstuff: Study on the Influence of Sample Dimensions with a FEM Approach. Journal of Food Engineering, 71, 233-241. http://dx.doi.org/10.1016/j.jfoodeng.2004.11.036
- Ratanadecho, P., Aoki, K. and Akahori, M. (2002) A Numerical and Experimental Investigation of the Modeling of Microwave Heating for Liquid Layers Using a Rectangular Wave Guide (Effects of Natural Convection and Dielectric Properties). Applied Mathematical Modelling, 26, 449-472. http://dx.doi.org/10.1016/S0307-904X(01)00046-4
- Zhang, Q., Jackson, T.H. and Ungan, A. (2000) Numerical Modeling of Microwave Induced Natural Convection. Jour- nal of Heat and Mass Transfer, 43, 2141-2154. http://dx.doi.org/10.1016/S0017-9310(99)00281-1
- Salvi, D., Boldor, D., Aita, G.M. and Sabliov, C.M. (2011) COMSOL Multiphysics Model for Continuous Flow Microwave Heating of Liquids. Journal of Food Engineering, 104, 422-429. http://dx.doi.org/10.1016/j.jfoodeng.2011.01.005
- Bird, R.B., Stewart, W.E. and Lightfoot, E.N. (2002) Transport Phenomena. 2nd Edition, John Wiley and Sons, Inc.
- Zhu, J., Kuznetsov, A.V. and Sandeep, K.P. (2007) Mathematical Modeling of Continuous Flow Microwave Heating of Liquids (Effects of Dielectric Properties and Design Parameters). International Journal of Thermal Sciences, 46, 328-341. http://dx.doi.org/10.1016/j.ijthermalsci.2006.06.005
Nomenclature
NOTES
*Corresponding author.




















