Engineering
Vol.6 No.8(2014), Article
ID:47751,14
pages
DOI:10.4236/eng.2014.68041
Spatio-Temporal Kinematic Decomposition of Movements
Dimitri Volchenkov1,2*, Bettina E. Bläsing1,3,4, Thomas Schack1,3,4
1Cognitive Interaction Technology-Center of Excellence (CITEC), Bielefeld University, Bielefeld, Germany
2Department of Physics, Bielefeld University, Bielefeld, Germany
3Department of Neurocognition and Action Biomechanics, Bielefeld University, Bielefeld, Germany
4Research Institute for Cognition and Robotics (CoR-Lab), Bielefeld University, Bielefeld, Germany
Email: *volchenk@physik.uni-bielefeld.de
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 April 2014; revised 27 May 2014; accepted 8 June 2014
ABSTRACT
We propose the new experimental method for investigating and approximating the organization and structure of movements with given accuracy. The composition of approximating trajectories illuminating the movement traits discloses the level of movement expertise in dancers and golf players. The method allows estimating the level of movement expertise, drawing the detailed structure of movements, and classifying movements into a given repertoire automatically.
Keywords:Kinematic Structure of Movements, Spatio-Temporal Kinematic Decomposition of Movement, Complexity of Movements, Complexity of Shape Changes, Automated Classification of Movements

1. Introduction
The modern technologies of motion tracking provide researchers with a wealth of kinematic data on the fullbody movements of humans, animals, and various robotic platforms. In order to explore the rich data, we have created computationally feasible algorithms for decomposing movements into independent spatio-temporal features directly from the captured kinematic signal. The proposed approach is useful for understanding, interpreting, and modelling complex movements in systems possessing many degrees of freedom, and provides a means for examining the overall structure of a movement.
Movements of markers arranged on a dancer’s body include motion of the skeletal system, motility of skin and tissues relative to the skeletal system, sliding of markers fixed on the clothing relative to the body, etc. In our work, we address questions concerning the interpretation of the captured kinematic data which remain far beyond the scope of usual biomechanical studies focusing on the time course of anatomical joint angles and searching for specific kinematic patterns within human motion: Which scale of movements are we interested in studying? Is it possible to filter out unsolicited scales of motion in a statistically consistent way? Is it possible to figure out the part of a recorded movement which is predefined by the goal and the style of a movement, independently of the subject, and the part that represents the individual movement traits of the subject and is perhaps influenced by his emotional and physical states? In particular we discuss some simple mathematical methods that can be useful for analyzing a wealth of motion capture data. The aims of the study were to find the computationally simple algorithms for eliciting differences in the kinematic signals captured from dancers and golf players of different skill-levels, for finding the detailed structure of motion by analyzing recorded kinematic signals, and for automatic classification of movements from a given repertoire.
In our work devoted to the kinematic analysis of complex full-body movements in classical ballet and a golf swing, we show that a movement tracked by a motion tracking system (MTS) can be understood in terms of a hierarchy of major and minor scales, in which the spatial and temporal components can be separated and studied independently. Based on our Spatio-Temporal Kinematic Decomposition (STKD) method, the major structure of a movement can be assessed. Specifically, the affinity between markers is identified by measuring the distance between them in the largest scale of kinematic signal, and by visualising the results via a dendrogram. This approach reveals the functional relationship between markers by their geometric proximity. The typical character of movement is featured by the few major scales, while the minor scales determine the individual movement traits and can uniquely disclose the individual level of movement expertise, uneven distribution of the fine motor skills, and the emotional character of an individual. The functional separation of scales can explain why we can perceive movements categorically (for example, as the highly stylized figures of classical ballet).
The suggested algorithms have been tested on recorded movements from classical ballet and golf, and they allow us to estimate the level of movement expertise, draw the detailed structures of arbitrary complex movements, and automatically classify them into a given repertoire.
2. Methods and Participants
To track movements, we used a MTS (Vicon Motion Systems, Inc.) based on 12 high-resolution cameras outfitted with IR optical filters and rings of LED strobe lights streaming data at 200 fps; the cameras detected the 3-dimensional spatial positions of passive retro-reflective spherical body markers with millimeter accuracy. Markers were attached to key anatomical locations according to the standard Vicon full-body marker placement protocol (Plug-in Gait) (see Figure 1).
In our study of figures in classical ballet, we have chosen the movement sequences that are considered basic movement vocabulary of classical dance, and are part of the daily routine of professional dancers as well as of the common training session of amateur ballet dancers: petit pas sauté (a small jump on both feet), petit pas jeté (a small jump from one foot to the other), petit pas assemblé (a small jump from one foot to both feet), petit pas echappé (a small jump on both feet to an open position), pas jeté (a jump from one foot to the other) and pirouette en dehors (a sequence of turns on one leg in the direction of the non-supporting leg). These movements were chosen because of their high degree of familiarity among professional and amateur dancers, and because of their ubiquity even in beginners’ classes. Participants were 22 young dancers (18 girls and 4 boys aged 13 - 17 years, which reflects a typical gender ratio for ballet amateurs of this age) studying at the Dance Department of the Essen-Werden Gymnasium which aims at young people of school ages aspiring to a career in professional ballet, and two professional ballet dancers (1 man, 1 woman) from the Staatsballett Berlin and Aalto Ballet Theater Essen. All participants performed repeated trials for each of the six figures of classical ballet which had been consequently recorded in several motion capture sessions and translated on to the digital models of movements (in total, 557 recorded trials were analyzed).
In our study of the movement kinematics of a golf swing in 9 participants (Mage = 32.3, SDage = 10.6, 6 male) of varying skill levels (0 to 50 years of golf experience). Specifically, movement kinematics of a golf swing were captured using a 3-dimensional motion tracking system (Vicon Motion Systems, Inc.) in which markers were placed on the anatomical landmarks of the body consistent with the standard Vicon full-body Plug-in Gait marker placement protocol.
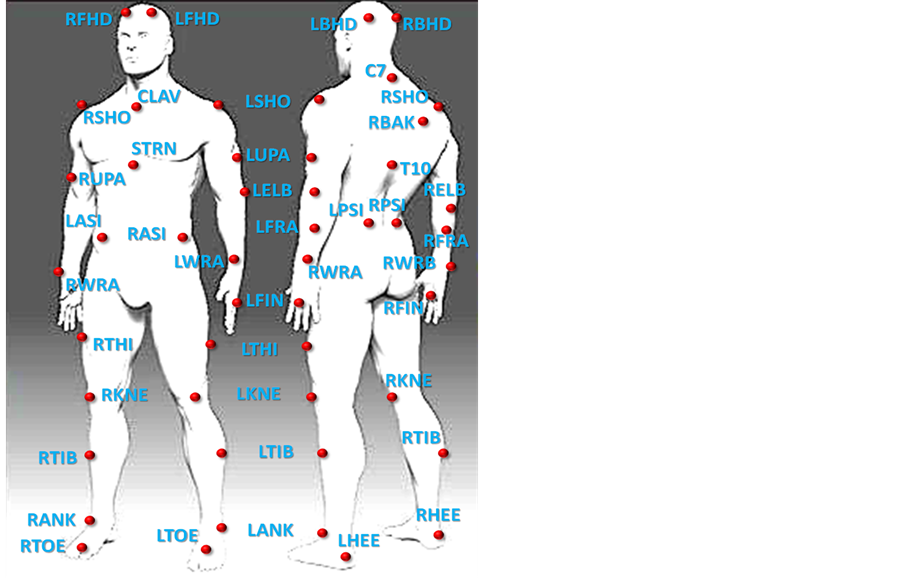
Figure 1. Location of the passive retro-reflective spherical body markers arranged on the dancer’s body in relation to the human skeletal system.
3. Scale Decomposition of Kinematic Data
The MTS delivers positional data for N markers, across T time frames (![]() ) at the rate of 200 fps, in the form of a rectangular 3N × T matrix
) at the rate of 200 fps, in the form of a rectangular 3N × T matrix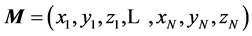 , in which the consequent triples of columns,
, in which the consequent triples of columns,
 ,
,  ,
, 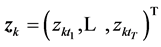 , represent the Cartesian coordinates of the markers k = 1,···,N, at the sequent time frames
, represent the Cartesian coordinates of the markers k = 1,···,N, at the sequent time frames . The T sign indicates transposition. The data matrix M is factorized using the singular value decomposition (SVD),
. The T sign indicates transposition. The data matrix M is factorized using the singular value decomposition (SVD),
 (1)
(1)
where the ⊗ sign stands for the outer product of vectors, U is a 3N × 3N unitary matrix with the columns us representing the left singular vectors of M, V is a T × 3N unitary matrix with the columns vs representing the right singular vectors of M, and Ʃ is a 3N × 3N diagonal matrix of ordered non-negative scale factors (singular values):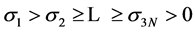 . A number of smallest singular values can be equal to zero if the MTS suffers from optical occlusion. Moreover, a number of left and right singular vectors can belong to the same singular value if the matrix M enjoys an exact spatio-temporal symmetry. However, while processing the actual motion tracking data, we have never encountered multiple singular values. If all singular values of M are non-degenerate and non-zero, then the factorization (1) is unique, up to simultaneous multiplication of the left and right eigenvectors by the same unit phase factor. The left singular vectors form an orthonormal basis for the spatial arrangement of markers,
. A number of smallest singular values can be equal to zero if the MTS suffers from optical occlusion. Moreover, a number of left and right singular vectors can belong to the same singular value if the matrix M enjoys an exact spatio-temporal symmetry. However, while processing the actual motion tracking data, we have never encountered multiple singular values. If all singular values of M are non-degenerate and non-zero, then the factorization (1) is unique, up to simultaneous multiplication of the left and right eigenvectors by the same unit phase factor. The left singular vectors form an orthonormal basis for the spatial arrangement of markers, 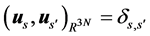 , with respect to the inner product in
, with respect to the inner product in . The right singular vectors are orthonormal with respect to the inner product in
. The right singular vectors are orthonormal with respect to the inner product in ,
, 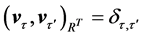 , forming a basis for the temporal sequences of kinematic data. With the use of (1), the kinematic signal M is decomposed into a weighted, ordered sum of separable matrices
, forming a basis for the temporal sequences of kinematic data. With the use of (1), the kinematic signal M is decomposed into a weighted, ordered sum of separable matrices 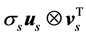 in which the information about the spatial arrangement of markers corresponding to the singular value σs is represented by the vector us separately from the vector vs, giving an account of the temporal evolution. For each non-degenerate singular value, the separable matrix
in which the information about the spatial arrangement of markers corresponding to the singular value σs is represented by the vector us separately from the vector vs, giving an account of the temporal evolution. For each non-degenerate singular value, the separable matrix  is a rank-one 3N × T matrix describing a one-dimensional mapping of spatial locations of markers to the sequent time frames that correspond to the synchronous motion of all markers (although with variable velocity) along straight lines. Namely, the trajectories of markers specified by the consequent triples of columns
is a rank-one 3N × T matrix describing a one-dimensional mapping of spatial locations of markers to the sequent time frames that correspond to the synchronous motion of all markers (although with variable velocity) along straight lines. Namely, the trajectories of markers specified by the consequent triples of columns 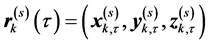 of the matrix
of the matrix  can be described mathematically using a single spatial dimension. Let us denote with
can be described mathematically using a single spatial dimension. Let us denote with ![]() the unit vector, tracing the direction of the linear motion of the kth marker at the scale σk,
the unit vector, tracing the direction of the linear motion of the kth marker at the scale σk,

and the amplitude function of the linear motion common for all markers by
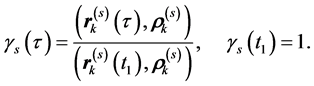
Then, the trajectory  of the kth marker recoded by the MTS can be represented by the ordered sum of linear trajectories,
of the kth marker recoded by the MTS can be represented by the ordered sum of linear trajectories,
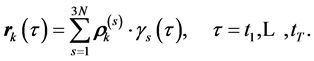 (2)
(2)
The SVD of trajectories into linear components given by (2) is obvious for the motion of a single marker (see Figure 2) along a planar elliptic trajectory segment. In such a simple case, the components ![]() and
and ![]() are nothing but the major and minor axes of the ellipse. It is clear that the amplitude functions for the bigger and smaller scales of motion are
are nothing but the major and minor axes of the ellipse. It is clear that the amplitude functions for the bigger and smaller scales of motion are 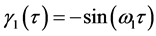 and
and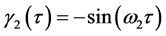 , respectively.
, respectively.
Application of SVD in data analysis is similar to the well-known principal component analysis and Fourier analysis [1] . By setting the small singular values to zero, we obtain the minimal set of independent spatio-temporal features, ordered according to the scales of motion, which then approximate the original data with a maximal precision. Namely, for l < 3N, the 3N × T matrix  renders the best least square approximation to M of the rank—ℓ, with an error smaller than the first neglected eigenvalue σℓ + 1. By neglecting
renders the best least square approximation to M of the rank—ℓ, with an error smaller than the first neglected eigenvalue σℓ + 1. By neglecting
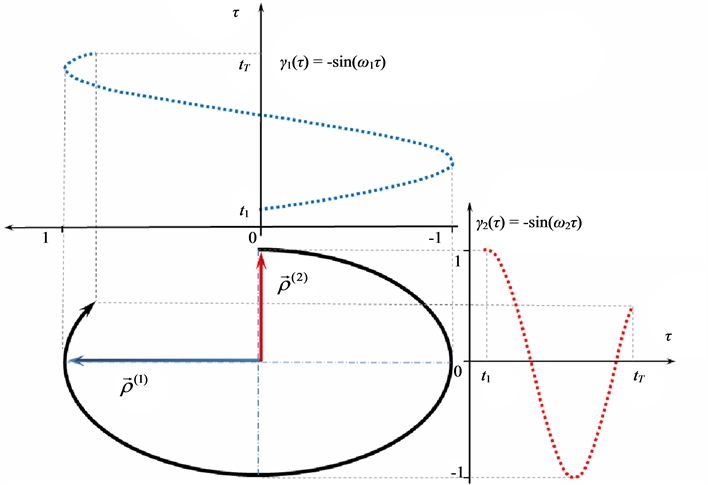
Figure 2. The scale decomposition of a plane elliptic trajectory segment.
the scales σs > ℓ in (1) and consequent recombination of the kinematic signal, we can filter out unsolicited scales of motion (e.g., small scale movements of markers fixed on the clothing instead of the skin, movements of skin and tissues relative to the skeletal system, etc.) Despite certain computational similarity, the method of SVD differs essentially from the latent variable models, such as factor analysis, which use regression modeling techniques to test hypotheses producing error terms. The decomposition (1) does not involve any statistical hypotheses, being a purely descriptive technique.
4. Assessing Complexity of Trajectories
The decomposition of a movement into a number of linear constituents (2) allows for assessing its complexity. Namely, each 3N × T principal matrix 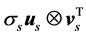 describing the movement scale
describing the movement scale 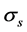 subsumes a portion of recorded movements,
subsumes a portion of recorded movements,
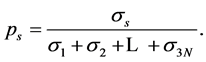 (3)
(3)
In case of a synchronous linear motion of all markers, 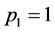 , while
, while , for all
, for all![]() . In general, the value of
. In general, the value of  depends upon the number of mounted markers, the exact anatomical positions of markers, as well as on individual features of subject’s anatomy. Nevertheless, if the motion capture session is conducted in a fixed laboratory setting, and the experimenters regard uniform principles for placing markers on subject’s body, then the major scales of the rank-value distribution function for
depends upon the number of mounted markers, the exact anatomical positions of markers, as well as on individual features of subject’s anatomy. Nevertheless, if the motion capture session is conducted in a fixed laboratory setting, and the experimenters regard uniform principles for placing markers on subject’s body, then the major scales of the rank-value distribution function for  allow easy comparison of different movements. An alternative way of presenting the decrease of singular values is to make a plot of the cumulative distribution function for
allow easy comparison of different movements. An alternative way of presenting the decrease of singular values is to make a plot of the cumulative distribution function for ,
,
 (4)
(4)
which ascertains a portion of a movement contained in the best least square approximation of the recorded data by a matrix of rank s. Such a plot has the advantage that it reduces the noise in the tail of the rank-value distribution for 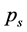 and can reveal the level of subject’s expertise in performing the movement. Skewness of the rankvalue distributions for the
and can reveal the level of subject’s expertise in performing the movement. Skewness of the rankvalue distributions for the 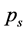 values can be characterized by the entropy-like spectral parameter, which we call the entropy of trajectories,
values can be characterized by the entropy-like spectral parameter, which we call the entropy of trajectories,
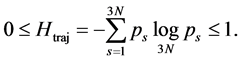 (5)
(5)
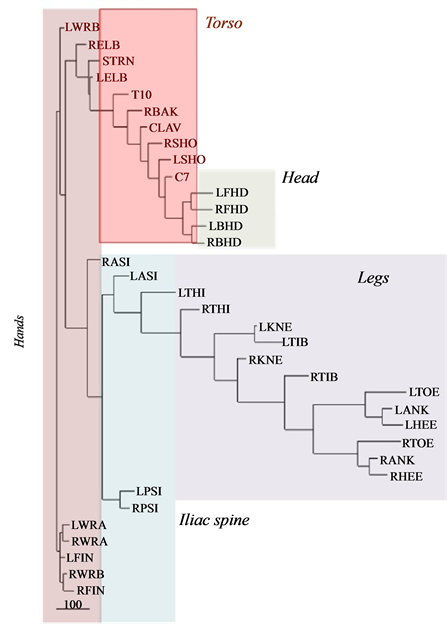
It equals zero for a linear movement, but takes value 1 when temporal and spatial dependence in the movement cannot be separated, i.e. when all singular values are equal. The parameter 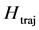 can be used as a quantitative measure of the degree of diversity of the set of linear trajectories required to approximate recorded movements with a maximal precision. Due to the base of logarithm depending on the number of used markers, the entropy of trajectories can be compared for kinematic signals attested with the different numbers of markers.
can be used as a quantitative measure of the degree of diversity of the set of linear trajectories required to approximate recorded movements with a maximal precision. Due to the base of logarithm depending on the number of used markers, the entropy of trajectories can be compared for kinematic signals attested with the different numbers of markers.
5. Analyzing Movement Structures
Scale decomposition of tracked movements can be used as a base for the functional alignment of markers. Spatio-temporal relationships between different body parts in evolving movements can be visualized by a dendrogram representing the relative distance between markers on the largest scale of movement through the horizontal branch length. In accordance with (2), a motion can be understood in terms of a hierarchy of scales evolving by . The lowest level of this hierarchy corresponds to fast, low-scale movements of markers fixed on the clothing relative to the body, whereas the highest levels encode relatively slow, large-scale movements of the skeletal system. Although a detailed analysis of the functions
. The lowest level of this hierarchy corresponds to fast, low-scale movements of markers fixed on the clothing relative to the body, whereas the highest levels encode relatively slow, large-scale movements of the skeletal system. Although a detailed analysis of the functions 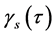 lies beyond the scope of the present paper, it is worth mentioning that they typically constitute strongly anharmonic oscillations, indicating that the relationship between force and displacement at each movement scale is strongly non-linear.
lies beyond the scope of the present paper, it is worth mentioning that they typically constitute strongly anharmonic oscillations, indicating that the relationship between force and displacement at each movement scale is strongly non-linear.
Being primarily concerned with the movement on its largest scale, we note that its structure is determined in (2) by the spatial arrangement of vectors ![]() in association with the markers
in association with the markers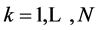 . For each markerthe magnitude of the corresponding vector
. For each markerthe magnitude of the corresponding vector 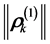 can be considered as a relative measure of its mobility on the movement scale σs, since the total path of the k-marker is proportional to the corresponding magnitude,
can be considered as a relative measure of its mobility on the movement scale σs, since the total path of the k-marker is proportional to the corresponding magnitude,
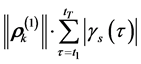 . The degree of affinity between a pair of markers, k1 and k2, can be attested on the largest scale of the movement by means of the Euclidean distance between the related vectors,
. The degree of affinity between a pair of markers, k1 and k2, can be attested on the largest scale of the movement by means of the Euclidean distance between the related vectors,
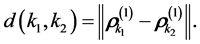 (6)
(6)
It is customary to reproduce the matrices of all-to-all distances in the form of a dendrogram by placing closely-related markers in the same mold. To preserve the structure (6) as much as possible, we use the standard neighbor-joining tree-generating algorithm [2] . We search the matrix (6) for the closest markers, and then connect them into a block. Once the markers are connected, they are removed from the distance matrix and replaced by the block connecting them. The neighbor-joining algorithm continues until all N markers are connected in a tree, and each branch acquires a length, with length being interpreted as the estimated number of substitutions required to resolve the block. The functional contingency between blocks of markers on the largest scale of the movement is disclosed by their geometric proximity in the resulting dendrogram. In spite of all participants sharing roughly the same anatomy and performing the same movements, the structures of calculated dendrograms can be substantially different in terms of individual movement features and level of movement.
6. Analysis of Body Shape Changes in Movements
Proper alignment of postures and turnout of the legs (outward rotation from the hip joints) are vital for both excellent performance and aesthetic perception of ballet figures. Well-composed movements, in which the relative positions of certain body parts hold for a while along the main trajectories, can be ascertained from the analysis of relative kinematics of markers placed on the dancer’s body. In order to track changes in body shape of a dancer during the performance of ballet steps, we have used the Procrustes analysis [3] which is customary in shape matching and shape recognition, as it allows consequent subtraction of all Euclidean transformations (translations, scaling, and rotations) preserving the relative spatial configuration of markers.
We move the origin of the frame of reference into the instantaneous geometrical center  of the trunk calculated with respect to the trunk markers at each time frame
of the trunk calculated with respect to the trunk markers at each time frame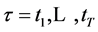 . After a simple transformation removing the translational and scaling components of the movement,
. After a simple transformation removing the translational and scaling components of the movement,
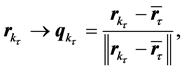 (7)
(7)
any displacement of a marker in physical space is represented by a pure rotation connecting the points on the surface of a unit sphere centered at  Given the instantaneous positions of all markers at two consequent time steps,
Given the instantaneous positions of all markers at two consequent time steps,  and
and 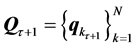 we rotate
we rotate  around the origin seeking for the optimal return rotation
around the origin seeking for the optimal return rotation 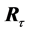 that minimizes the least square distance,
that minimizes the least square distance, 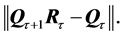 The inverse rotation matrix
The inverse rotation matrix  represents the averaged movement of the whole of markers during the specific interval of time between frames. The final transformation,
represents the averaged movement of the whole of markers during the specific interval of time between frames. The final transformation,
 (8)
(8)
removes those averaged movements from the kinematic signal, consequently for all time frames up to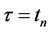 . While the relative positions of markers persist, the transformations defined above do away with the kinematic signal completely. Therefore, the changes in the dancer’s body shape registered at the marker
. While the relative positions of markers persist, the transformations defined above do away with the kinematic signal completely. Therefore, the changes in the dancer’s body shape registered at the marker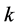 , at the time frame
, at the time frame 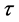 can be evaluated by the shape difference vector,
can be evaluated by the shape difference vector,
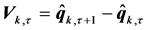 (9)
(9)
where 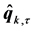 is the transformed kinematic signal.
is the transformed kinematic signal.
7. Assessing Complexity of Body Shape Changes
To assess the complexity of changes in body shape, we implement the method of biorthogonal decomposition (BOD) [4] , as each entry of the matrix ![]() constitutes a vector, so that the standard SVD method cannot be used. We decompose the Hermitian, non-negative definite correlation operators,
constitutes a vector, so that the standard SVD method cannot be used. We decompose the Hermitian, non-negative definite correlation operators,
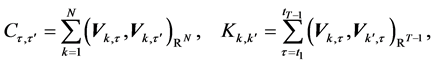 (10)
(10)
into a set of proper orthogonal spatial eigenmodes ![]() and proper orthogonal temporal eigenmodes
and proper orthogonal temporal eigenmodes  which share the same eigenvalues
which share the same eigenvalues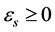 ,
,
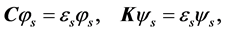 (11)
(11)
eigenvalues 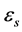 are common to
are common to ![]() and
and 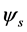 due to the symmetry property of the correlation operators (10) [4] . Each spatial eigenmode
due to the symmetry property of the correlation operators (10) [4] . Each spatial eigenmode ![]() is associated with an instantaneous coherent structure which has a temporal evolution directly given by the corresponding temporal eigenmode
is associated with an instantaneous coherent structure which has a temporal evolution directly given by the corresponding temporal eigenmode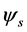 . The global entropy of the signal characterizing its degree of disorder is defined starting from the eigenvalues
. The global entropy of the signal characterizing its degree of disorder is defined starting from the eigenvalues ,
,
 (12)
(12)
We call this spectral parameter the entropy of shape. When changes in shape evolve coherently being simultaneously registered in all markers, 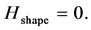 In the opposite case, if the changes appear chaotically,
In the opposite case, if the changes appear chaotically, 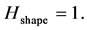 The entropy of shape (12) can be compared for different kinematic signals captured from different motions performed by a subject, as well as from the motion performed by different participants. We have to emphasize that the entropy of shape (12) measuring complexity of the kinematic signal, after subtracting shape preserving Euclidean transformations, is essentially distinct from the entropy of trajectories defined in (5) as a measure of diversity of a set of linear trajectories required for a reliable approximation of recorded movements.
The entropy of shape (12) can be compared for different kinematic signals captured from different motions performed by a subject, as well as from the motion performed by different participants. We have to emphasize that the entropy of shape (12) measuring complexity of the kinematic signal, after subtracting shape preserving Euclidean transformations, is essentially distinct from the entropy of trajectories defined in (5) as a measure of diversity of a set of linear trajectories required for a reliable approximation of recorded movements.
8. Results and Discussion
8.1. The Composition of Approximating Linear Trajectories Features the Movement Traits and Discloses the Level of Movement Expertise in Participants
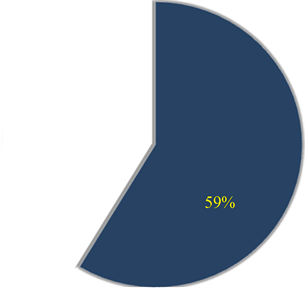
Ranked singular values of the data matrices describing trajectories of markers decrease very fast for all tracked movements, which indicates that the recorded kinematic signals are characterized by a strong hierarchy of scales. The most kinematic information about a movement is held by just a few major scales. In Figure 3, we have presented the sequent recombination of tracked movements for a pirouette en dehors performed by an expert. On the largest scale aggregating 59% of the recorded data, the movements of markers in the pirouette are approximated by straight lines (see Figure 3(a)). Figure 3(b) shows the best approximation of the captured movements by 2-dimensional plane curves (encompassing 68% of the kinematic data). In Figure 3(c), the movements of markers are approximated by space curves described by the three major movement scales representing together 75% of the data. Eventually, in Figure 3(d), we have presented the complete set of trajectories recorded during the performance.
It is worth mentioning that in general the decrease of ranked singular values for the motion data tracked in experts was more gradual than in novices. In Figure 4, we have presented the logarithmic plot opposing the averaged cumulative distributions 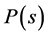 for the pirouette en dehors performed by students (shown by the dashed line) and by experts (shown by the continuous line). The averaged cumulative distribution of
for the pirouette en dehors performed by students (shown by the dashed line) and by experts (shown by the continuous line). The averaged cumulative distribution of 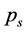 for the data collected from the pirouettes performed by students always dominates indicating that fewer movement scales are required to reproduce the same portion of tracked data in students than in experts. Usually, trajectories recorded during the trials performed by students were simpler than those observed in experts, as being approximated by lower rank matrices, with the same degree of accuracy. Consequently, the entropy of trajectories calculated on the data recorded in experts was typically higher than on the data recorded in students. We do not observe any clear gender difference in kinematic signals recorded from the ballet steps. Despite an individual character of variations in the tails of rank-value distributions for
for the data collected from the pirouettes performed by students always dominates indicating that fewer movement scales are required to reproduce the same portion of tracked data in students than in experts. Usually, trajectories recorded during the trials performed by students were simpler than those observed in experts, as being approximated by lower rank matrices, with the same degree of accuracy. Consequently, the entropy of trajectories calculated on the data recorded in experts was typically higher than on the data recorded in students. We do not observe any clear gender difference in kinematic signals recorded from the ballet steps. Despite an individual character of variations in the tails of rank-value distributions for , the fiber of a movement is featured by the few major
, the fiber of a movement is featured by the few major
 (a)
(a)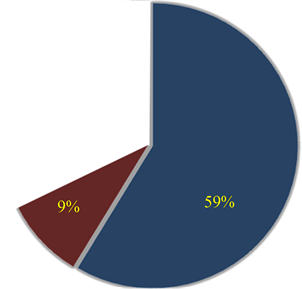 (b)
(b) (c)
(c)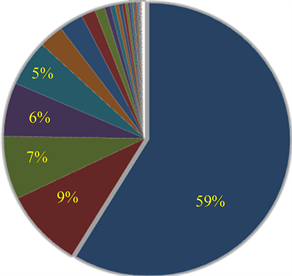 (d)
(d)
Figure 3. The sequent recombination of tracked movements (d) for a pirouette en dehors executed with 5 rotations by an expert. The pie-charts show the portions of the data matrix approximated by (a) the rank-one matrix, straight lines; (b) the rank-two matrix, plane curves; (c) the rank-three matrix, space curves.

Figure 4. The logarithmic plot opposing the averaged cumulative distributions 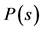 calculated for the pirouette en dehors performed by students (shown by the dashed line) and by experts (shown by the continuous line).
calculated for the pirouette en dehors performed by students (shown by the dashed line) and by experts (shown by the continuous line).
scales that appear utterly alike across all participants (whether experts or students) and all trials (whether successful or not) of the movement. In Figure 5, we juxtapose the values of 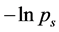 for five major movement scales in the data recorded from the successful trials of petit pas échappé and pirouette en dehors. Both movements show a sufficiently high degree of complexity. In both movements, coordination is important to facilitate the goal of the main functional phase, a jump in the petit pas échappé, and a turn in the pirouette en dehors. There are, however, crucial differences in the biomechanical structure between the two movements that make them worthy of comparison. The systematic differences in the values of entropy of trajectories calculated for the data recorded from different ballet figures attest to substantial disparity in the related rank-value distributions of
for five major movement scales in the data recorded from the successful trials of petit pas échappé and pirouette en dehors. Both movements show a sufficiently high degree of complexity. In both movements, coordination is important to facilitate the goal of the main functional phase, a jump in the petit pas échappé, and a turn in the pirouette en dehors. There are, however, crucial differences in the biomechanical structure between the two movements that make them worthy of comparison. The systematic differences in the values of entropy of trajectories calculated for the data recorded from different ballet figures attest to substantial disparity in the related rank-value distributions of .
.
8.2. Movement Structures in pirouette en dehors and a Golf Swing
In Figure 6 and Figure 7, we have shown the neighbor-joining dendrograms representing the functional alignment of markers in the pirouette en dehors performed by a professional ballet dancer and a novice, respectively. To visualize spatio-temporal relationships between markers on the major scale of recorded movements, we have used the TreeView software, which is freely available on the internet [5] . The pirouette en dehors, a controlled turn away from the supporting leg, is one of the most difficult of all ballet steps that can be executed with single or multiple rotations. The proper turning technique includes a periodic, rapid rotation of the head that serves to fix the dancer’s gaze on a single spot, helping her to maintain control over the body (known as spotting). This rotational movement requires highly-defined coordination and constant adjustment of the body axis in order to be performed with the required stability and accuracy [6] . The rhythmic structure of the pirouette en dehors is described by [7] as four measures in two-four time, the first two measures containing the preparation, and the second two measures containing the turn and conclusion. According to this approach, the pirouette en dehors consists of two parts, the preparation and the actual turning movement. Both of these parts can be dissected again; the preparation can be broken down into two rhythmically-separated sections, whereas the turn segment consists of the actual turning movement and the opening to the front that concludes the turn. The dendrogram shown in Figure 6 discloses the functional structure of the pirouette en dehors on the left leg, executed by an expert. On the largest scale of the movement, the pirouette starts (at the upper right corner of the dendrogram) with the function of body alignment by arranging legs in the proper position: the right foot is placed in front of the left foot, both turned outward. The right foot slides to the side (tendu, or dégagé), which concludes the body alignment phase. The spring tension is built up for the turn during the tension build-up phase, as the right foot
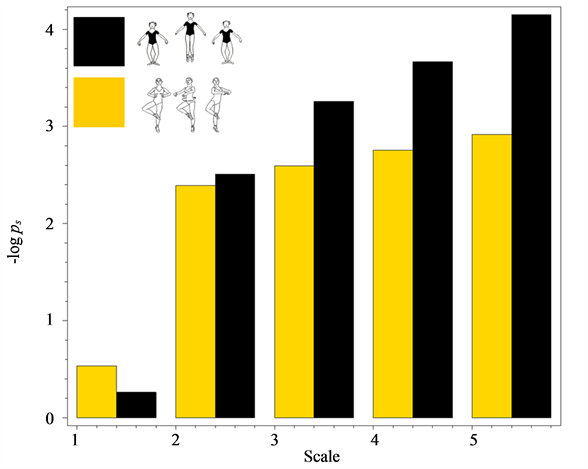
Figure 5. The values of 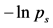 for five major movement scales in the data recoded from the successful trials of petit pas échappé and pirouette en dehors.
for five major movement scales in the data recoded from the successful trials of petit pas échappé and pirouette en dehors.

Figure 6. Functional alignment of markers in pirouette en dehors performed by a professional ballet dancer. The standard Vicon Plug-in Gait marker notations are used.

Figure 7. Functional alignment of markers in pirouette en dehors performed by a student. The standard Vicon Plug-in Gait marker notations are used.
moves back and is placed behind the left one and the knees bend (plié). At the beginning of the turn phase, both legs push into the ground and the left (supporting) leg adopts point or demi-point position (on the toes or on the ball of the foot, respectively), while the right knee is bent and the right foot is pulled up to the knee of the supporting leg. During the turn, the head is rapidly whipping around, which helps the dancer to maintain balance. Eventually, in the landing phase concluding the turn, the right foot is placed behind the left one, and the knees bend and stretch (plié). The arms open, and the arms and torso are used to cease rotation. It is important to mention that each functional phase elicited from the dendrogram shown in Figure 6 can be ascribed directly to the functional phases of the pirouette en dehors as defined in [8] via the Basic Action Concepts (BACs), the key points within the functional structure of the movement which are stored in the long-term memory of a dancer.
In contrast to the movement sequence executed by the professional dancer, the movement of a novice performer inappropriately starts simultaneously in both legs, and turning starts prematurely, while straightening the knees (see Figure 7). In the turning phase, the movements are allocated to the superior iliac spine. The head apparently does not play a role until ceasing the movement. Instead, the vigorous hand movements play a major role in maintaining the body’s rotation, which is a common mistake among beginners.
In Figure 8, we have presented the functional alignment of markers in a golf swing of an amateur (Figure 8(a)) and an expert (Figure 8(b)). It is remarkable that while the dendrogram representing the golf swing performed by the amateur reveals the central role of hands in the structure of movement, connecting the other parts of the body, the structure of movement in expert reveals the natural anatomical structure of human body.
8.3. Analysis of Body Shape Changes in pirouette en dehors
The results of Procrustes analysis applied to the kinematic data tracked from the pirouette en dehors executed by
 (a)
(a) (b)
(b)
Figure 8. Functional alignment of markers in a golf swing of (a) an amateur, (b) an expert. The functional alignment of markers in experts preserves the natural anatomical structure of human body.
a professional dancer is shown in Figure 9. The diagram represents the magnitude of the shape difference vector (3) calculated for each marker ![]() at the time frame
at the time frame  by subtraction of Euclidean transformations preserving the relative positions of markers. The magnitude
by subtraction of Euclidean transformations preserving the relative positions of markers. The magnitude 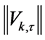 is sampled along the (horizontal) time axis with a time slice of 5 msec. The kinematic signal representing the shape changes in the pirouette en dehors has the form of two vertical bands exhibiting the onset and terminal phases of the movement, separated by the inertial phase, during which the relative positions of most of the markers, except for the head markers, remain unchanged in the chosen frame of reference. The synchronous shape change corresponds rather well to the blocks of markers matching the natural division of the skeletal system, as seen in Figure 9. The strong periodic signal from the four head markers spanning the whole inertial phase arises due to rapid rotation of the head while spotting.
is sampled along the (horizontal) time axis with a time slice of 5 msec. The kinematic signal representing the shape changes in the pirouette en dehors has the form of two vertical bands exhibiting the onset and terminal phases of the movement, separated by the inertial phase, during which the relative positions of most of the markers, except for the head markers, remain unchanged in the chosen frame of reference. The synchronous shape change corresponds rather well to the blocks of markers matching the natural division of the skeletal system, as seen in Figure 9. The strong periodic signal from the four head markers spanning the whole inertial phase arises due to rapid rotation of the head while spotting.
8.4. Automated Classification of Ballet Figures
We have assessed the diversity of trajectories (by the entropy of trajectories ) and complexity of shape changes (by the entropy of shape
) and complexity of shape changes (by the entropy of shape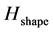 ) for 557 recorded trials of the six figures from the repertoire of classical ballet: petit pas sauté, petit pas jeté, petit pas assemblé, petit pas echappé, pas jeté, and pirouette en dehors, including the very complex pirouettes executed with 5 and 18 turns by professional ballet dancers. Each recorded trial, whether successful or not, has been taken into account, since a reliable motion classification method must be robust to individual variations in performance. The result of our analysis is presented in Figure 10 where all recorded ballet steps are classified in accordance with the entropy of trajectories and the entropy of shape. On the one hand, it is important to mention that the entropy of trajectories alone is vulnerable by individual variations in performance, as seen in extreme variability of its values calculated over the pull of 2-turn pirouettes performed by students. Moreover, the entropy of trajectories is obviously insensitive to recursion in movements: the pirouettes executed with different numbers of turns are characterized by the close values of the entropy of trajectories.
) for 557 recorded trials of the six figures from the repertoire of classical ballet: petit pas sauté, petit pas jeté, petit pas assemblé, petit pas echappé, pas jeté, and pirouette en dehors, including the very complex pirouettes executed with 5 and 18 turns by professional ballet dancers. Each recorded trial, whether successful or not, has been taken into account, since a reliable motion classification method must be robust to individual variations in performance. The result of our analysis is presented in Figure 10 where all recorded ballet steps are classified in accordance with the entropy of trajectories and the entropy of shape. On the one hand, it is important to mention that the entropy of trajectories alone is vulnerable by individual variations in performance, as seen in extreme variability of its values calculated over the pull of 2-turn pirouettes performed by students. Moreover, the entropy of trajectories is obviously insensitive to recursion in movements: the pirouettes executed with different numbers of turns are characterized by the close values of the entropy of trajectories.

Figure 9. The magnitude of the shape difference vector 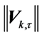 calculated for each marker k at the time frame
calculated for each marker k at the time frame  by subtraction of Euclidean transformations preserving the relative positions of markers.
by subtraction of Euclidean transformations preserving the relative positions of markers.
On the other hand, the entropy of shape alone is incapable of differentiating movements that evolve essentially from the same body shape changes, such as petit pas sauté, petit pas echappé, and petit pas jeté.
9. Conclusion
The STKD method presented in this paper allows for the segmentation of any recorded movement into a minimal number of independent spatial-temporal features. This method has been found to effectively elicit the hierarchically-organized key kinematic elements of a movement in different spatio-temporal scales. We have shown that a movement tracked by a motion tracking system can be understood in terms of a hierarchy of scales in which the spatial and temporal components are separated and can be studied singly. The typical character of individual movements from the classical ballet repertoire is featured by the few major scales, while minor scales determine the individual movement traits and can disclose the individual level of movement expertise. Such a functional separation of scales allows perceiving the movements categorically as the highly stylized figures of classical ballet. A choreographer translates the temporarily ordered sequences of ballet figures into a hierarchical structure of concepts transmuting dance into a kind of a sign language. In our work, we have proposed the quantitative measures for diversity and complexity of recorded human movements that can be used for the detailed
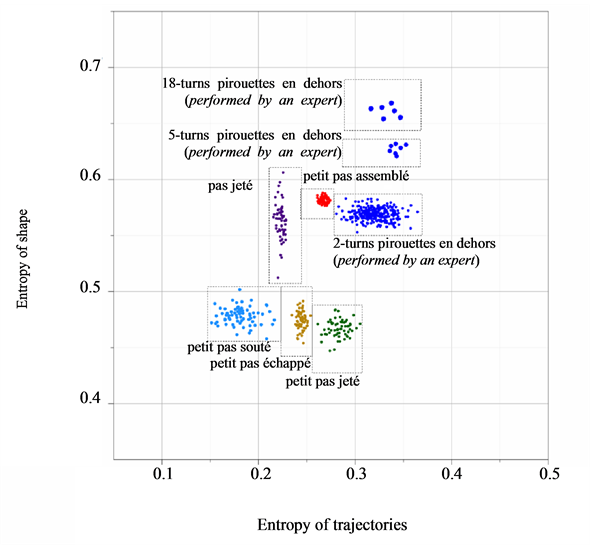
Figure 10. Based on the entropy of trajectories and the entropy of shape calculated for 557 recorded movement trials, we have them properly classified into the figures from the classical ballet repertoire.
analysis and comparison of kinematic signals captured from various movements performed by different participants. By bringing the important concept of entropy to the study of human movements, we have made a significant step toward understanding of how humans can convey—perhaps deliberately, but rather unintentionally— messages rich in content by using their own body as physical transmission medium. Implications of these findings are important for a number of movement related domains, including physical therapy, and sports training.
References
- Jolliffe, I.T. (1986) Principal Component Analysis. Springer, New York. http://dx.doi.org/10.1007/978-1-4757-1904-8
- Felsenstein, J. (2004) Inferring Phylogenies. Sinauer Associates Inc., Sunderland.
- Gower, J.C. and Dijksterhuis, G.B. (2004) Procrustes Problems. Oxford University Press, Oxford. http://dx.doi.org/10.1093/acprof:oso/9780198510581.001.0001
- Aubry, N., Guyonnet, R. and Lima, R. (1991) Spatiotemporal Analysis of Complex Signals: Theory and Applications. Journal of Statistical Physics, 64, 683-739. http://dx.doi.org/10.1007/BF01048312
- Page, R.D.M. (1996) TREEVIEW: An Application to Display Phylogenetic Trees on Personal Computers. Computer Applications in the Biosciences, 12, 357-358.
- Schack, T. (2001) On the Structure of Movement Representations—Theoretical Assumptions and Methodical Approach. Motor Control and Learning (E-Journal). http://www.ejournalbut.de/Journal/index.asp
- Tarassow, N.I. (2005) Klassischer Tanz. Die Schule des Tänzers. Henschel, Berlin.
- Bläsing, B., Tenenbaum, G. and Schack, T. (2009) Cognitive Structures of Complex Movements in Dance. Psychology of Sport and Exercise, 10, 350-360. http://dx.doi.org/10.1016/j.psychsport.2008.10.001
NOTES

*Corresponding author.

