Engineering
Vol. 3 No. 12 (2011) , Article ID: 9213 , 12 pages DOI:10.4236/eng.2011.312142
Probabilistic Simulation Approach to Evaluate the Tooth-Root Strength of Spur Gears with FEM-Based Verification
1Production Engineering and Mechanical Design Department, Faculty of Engineering, Mansoura University, Mansoura, Egypt
2Department of Mechanical Engineering, Stevens Institute of Technology, Hoboken, USA
E-mail: *eaziz@stevens.edu, cchassap@stevens.edu
Received October 13, 2011; revised November 1, 2011; accepted November 15, 2011
Keywords: Gear Design, Design for Uncertainties, Probabilistic Design, Reliability, FEM
ABSTRACT
Dependency on deterministic design techniques without attention to inherent process variations and uncertainties in gear design and manufacturing processes can lead to unreliable results and affect the performance of a gearing system. A better understanding of the impact of uncertainty associated with the system input on the system output can be achieved by including reliability techniques to accomplish a reliable design methodology. This emerged the need to consider the probabilistic behavior of the stress distribution on the gear tooth during the design phase. The present effort reports on the application of the Stress-Strength Interference (SSI) theory within the context of a “Design for Reliability” approach in support a detailed gear design methodology for the evaluation the tooth-root strength with FEM-based verification. The SSI theory is formulated to predict the effect of the root fillet generated by a rack or hob tool with and without protuberance on the gear system reliability. The results obtained from the probabilistic analysis strongly agreed with the FEM’ results across a range of different gear tooth fillet profiles. A quantitative assessment of the investigated gear sets showed the highest tooth-root stress was associated with the lowest tip radius of the generating tool. This approach helps with making the decision by quantifying the impact of stress and strength variations during the gear design stage.
1. Introduction
Traditional deterministic design approaches compensate for uncertainties through the use of empirical safety factors, which do not provide sufficient information to achieve optimal use of available resources in terms of material, manufacturing and operational costs [1]. For example, components resulting from such conventional design methods are either over-safe leading to wastage of resources or unsafe leading to unexpected failures. They fail to provide the necessary understanding of the variability associated with the properties of materials, manufacturing tolerances and in-service loading. To design a product that will perform a function reliably, the reliability must be considered as an important functional requirement all the way through the design process, from the customer’s need to the final product [2]. Addressing these issues comprehensively at an early design stage is necessary to produce competitive product that functions consistently during its intended service life [3]. Indeed, consistent levels of safety and reliability can be achieved based on the probabilistic design methods.
Probabilistic design, such as reliability-based design and robust design, offers tools for making reliable decisions with the consideration of uncertainty associated with design variables/parameters and simulation models [4,5]. It allows the designer to assess the reliability of the mechanical system. This is impossible with the factor of safety approach. One important task of a probabilistic design is uncertainty analysis, through which we understand how much the impact of the uncertainty associated with the system input is on the system output by identifying the probabilistic characteristics of system output. The uncertainty in a design performance is described probabilistically (e.g., Normal Distribution) by its mean (μ), variance (σ2), the probability density function (PDF), or the cumulative distribution function (CDF), etc. By understanding the probability distributions of the design parameters, the designer can design for a specific reliability or quality level by producing designs that are robust to variations. Figure 1 shows the difference between deterministic method and the SSI method as a probabilistic design tool for estimating reliability. The area representing the unreliability is a part of the area of the interference. The unreliability of the mechanical component is determined by the probability that the failure governing stress exceeds the failure governing strength. Once the failure governing stress and strength distributions are available, the unreliability or reliability of the component can be obtained by using the stress-strength distribution interference approach.
The life and reliability of mechanical systems such as the gearboxes depend on the life/reliability characteristics of their components at a certain defined load [6]. Gears, as the most important gearbox components, are relatively complex machine elements and there are many design parameters involved in their design. Their design methodology involves selecting appropriate attributes from a large amount of engineering/standards data available in catalogues and design handbooks [7]. Gears are generally designed based on endurance (fatigue characteristics) design standards. They should be selected and shaped to either endure a “nominal” i.e. rated load condition or unlimited load cycles. Stresses such as the bending stress at the tooth root under the nominal load must be below the endurance limit. The endurance limit values themselves are not “exact”, but “statistical”. For this reason, design standards such as AGMA, ISO, DIN, etc. include a number of factors such as size, surface, life, load, velocity, etc. to adjust the endurance limit “to be on the safe side”. However, the gear tooth strengths are obtained using deterministic models without sufficient knowledge of their statistical distribution. Furthermore, the variation in the gear tooth strength may also be affected by a combination of variations in the metallurgical and fabrication processes involved with its manufacture, dimensional inaccuracy, surface damage, etc., whereas fluctuations in the load imposed upon it may originate from variations in its duty and environment. Therefore, design of gears for specified design reliability may benefit from detailed distribution data of gear tooth strength.
There are two failure modes that are important causes of gear tooth failures. Bending stress (leading to tooth breakage) which is a maximum at the tooth root, and compressive stress (leading to pitting), which reaches a maximum value at the tooth face. Because the tooth loading is cyclic, both of these stress mechanisms impose a fatigue loading condition on this machine component element. Tooth breakage due to the stress concentration and crack initiation at the non-involute portion of gear tooth, when stresses significantly exceeds the maximum allowable stress in gear transmission units can be extremely dangerous in automotive, aerospace, or space industry applications. The non-involute portion of the tooth profile, the fillet, has a direct effect on the motion/force transmission. The detailed geometry of the fillet influences the maximum bending stresses developed at the root of the gear tooth and is determined by the gear cutting manufacturing process and cutting tool dimensions [8]. Hence, it is necessary to have a detailed knowledge of the root fillet geometry and its effect on the tooth bending stresses.
In the following sections, a special attention is given to the analysis of the impact of the gear tooth fillet portion on the maximum bending stress value and its distribution along the fillet portion. The SSI theory as a probabilistic design tool will be used to examine the influence of root fillet contour on the gear tooth strength for four gear sets with different fillet profiles.
2. Investigate the Effect of the Root Fillet Portion on the Gear Tooth Strength
According to the theory of gearing, the procedure for generating the exact geometry of the tooth profile must be modelled to follow the actual generation process which is used in production of real gears [9-11]. The generation of spur gear tooth shape during hobbing process is modelled to be equivalent to pure rolling of the pitch line of rack against the pitch circle of gear blank. The fillet curve of the gear belongs to the trochoid family and it is conjugate to the tip of the generating rack, as shown in Figure 2. The radius of curvature of the trochoid fillet varies along the fillet curve. In the following section, the mathematical model of the trochoid fillet is developed to investigate the effect of the trochoid fillet conditions on the root strength of the gear tooth.
Figure 2 shows an arbitrary position during a cycle of contact in a transverse plane between the generating hob tool and the gear tooth. According to AGMA 930-A05, the center of the rounded corner at the tip of the rack is located on the basic rack by its coordinates 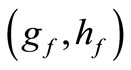

Figure 1. Comparison between deterministic method and the SSI method for estimating reliability. (a) Deterministic design; (b) Stress/strength interference.
relative to the nominal pitch line and the tooth center line. According to the geometric relationship depicted in Figure 2, it is found that:
 (1)
(1)
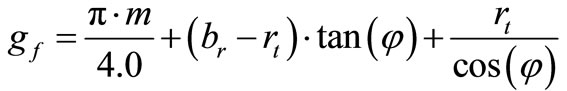 (2)
(2)
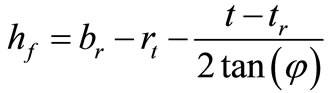 (3)
(3)
Each generated point on the trochoid is associated with a value of the pitch point polar angle . At the start of the trochoid, the pitch polar angle for the trochoid point on the root circle is
. At the start of the trochoid, the pitch polar angle for the trochoid point on the root circle is . At the tangent point with the involute profile, the pitch polar angle is
. At the tangent point with the involute profile, the pitch polar angle is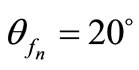 .
. 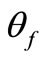 is the design parameter used to determine the trochoid fillet region and limited by
is the design parameter used to determine the trochoid fillet region and limited by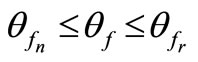 , which can be represented by the following equation:
, which can be represented by the following equation:
 (4)
(4)
where 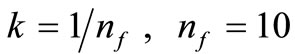
when the generating pitch line of the rack cutter rolls over the pitch circle of gear blank, the generating roll angle from a pitch point at tooth centerline to a pitch point at which (k) trochoid point is generated, as shown in Figure 2, can be defined by:
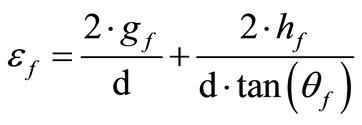 (5)
(5)
The Cartesian coordinates of any point 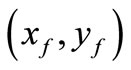 on the root fillet relative to gear tooth centerline can be obtained as follows:
on the root fillet relative to gear tooth centerline can be obtained as follows:
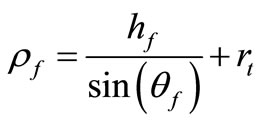 (6)
(6)
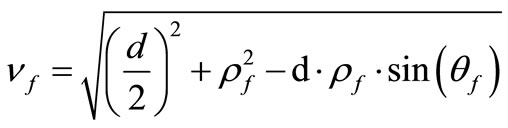 (7)
(7)
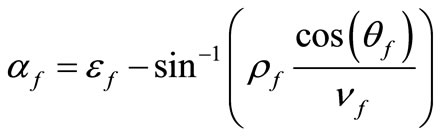 (8)
(8)
 (9)
(9)
Therefore, Equation (9) can be used to calculate the Cartesian coordinates of the envelope of trochoidal root fillets for four different cutter tip radius having 0.0, 0.25, 0.4 and 0.5 times the module. Figure 3 shows the generating hob tool and the trochoidal root fillet in an arbitrary position during a cycle of contact in a transverse plane for a gear with the number of teeth 20 (without undercut), module of 3 mm and pressure angle of 20˚. The center of the rounded corner at the tip traces out a trochoid and then, the rounded tip will envelope another curve defining the root fillet. Based on the numerical calculation results, the tooth profile in the transverse plane is produced and the teeth of the whole gear model are formed to build the complete 3D gear model.
During the meshing of gear pair, large localized stresses [12] occur in the fillets of gear teeth due to the sudden change in the cross-section of the tooth. Therefore, there is a need to examine the effect of these variations on gear tooth root strength. AGMA [13,14] has established an elastic behavior model for the gear tooth, which uses the Lewis parabola to determine the critical section by the tangency point of the parabola and the root trochoid . In Figure 4, it is apparent that the bending load component of the translated critical tooth
. In Figure 4, it is apparent that the bending load component of the translated critical tooth
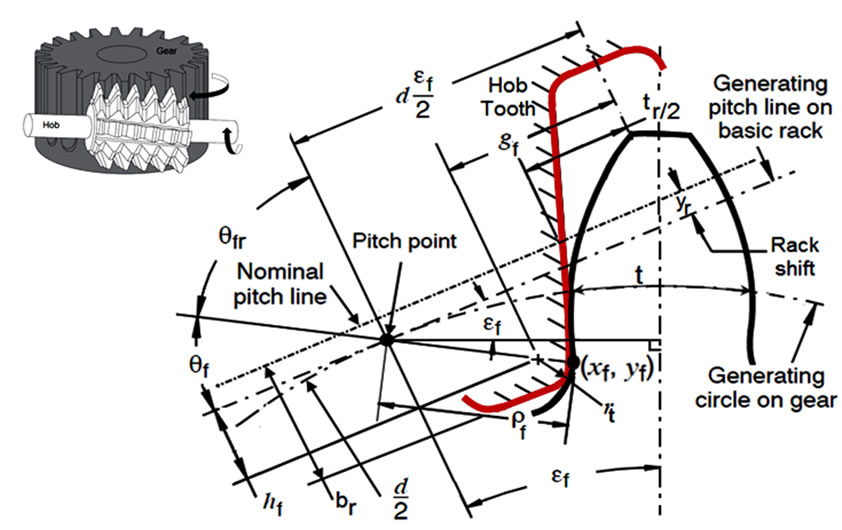
Figure 2. Kinematic relationship between the rack of hobbing cutter and generating gear tooth.
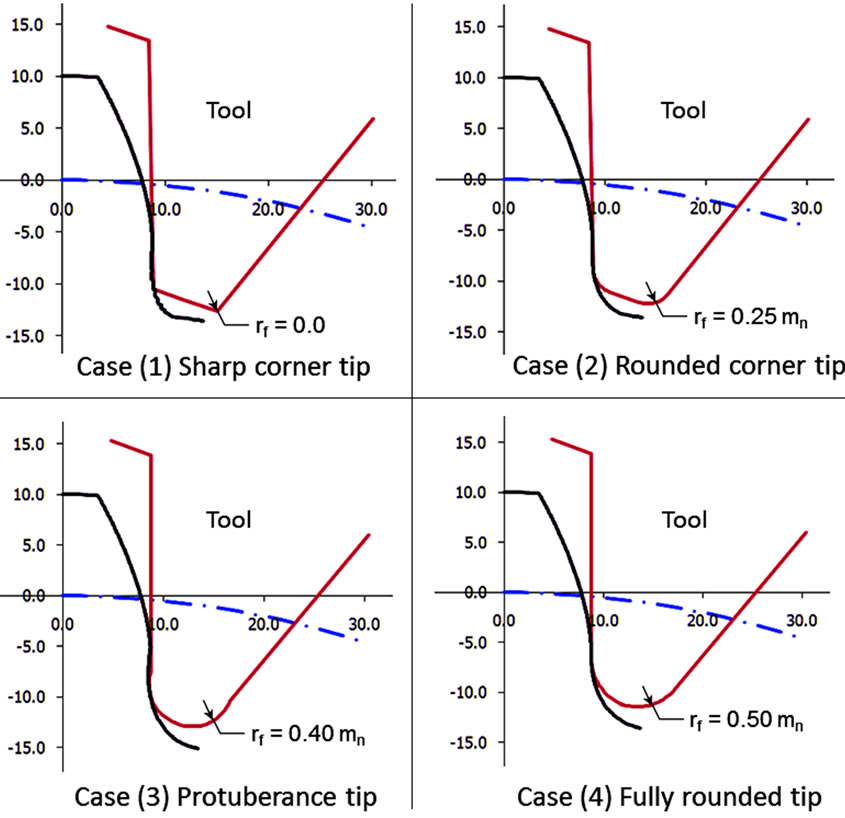
Figure 3. Fillet profile generated by different tip radius.
load 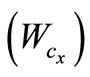 will produce the greatest bending stress at this critical section. The radial component
will produce the greatest bending stress at this critical section. The radial component 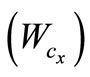 causes a small compressive stress across the root of the gear tooth. This causes the tensile stress to decrease by a small amount, and the compressive stress on the opposite side of the tooth to increase by a slight amount. In most materials, a tensile stress is more damaging than a slightly higher compressive stress. The stresses are analyzed on the tooth side loaded in tension because the first cracks are expected to appear there [15]. The combined tensile stress is the difference between the bending tensile and the compressive stresses, which can be obtained by the following equation:
causes a small compressive stress across the root of the gear tooth. This causes the tensile stress to decrease by a small amount, and the compressive stress on the opposite side of the tooth to increase by a slight amount. In most materials, a tensile stress is more damaging than a slightly higher compressive stress. The stresses are analyzed on the tooth side loaded in tension because the first cracks are expected to appear there [15]. The combined tensile stress is the difference between the bending tensile and the compressive stresses, which can be obtained by the following equation:
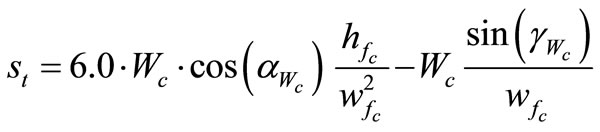 (10)
(10)
The critical tooth root cross section can be determined based either on the force application on the tip or the force application at the single point of action. In Equation (10),  is the height of the translated critical load above the critical section
is the height of the translated critical load above the critical section  in the tooth root, it is calculated from the following equation:
in the tooth root, it is calculated from the following equation:
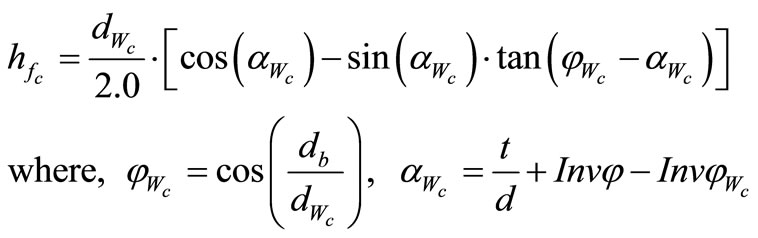 (11)
(11)
Based on the actual tooth form, the tooth form factor ( ) and the stress correction factor (
) and the stress correction factor (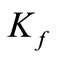 ) are calculated at the critical section in the tooth root area and subsequently the bending strength geometry factor (
) are calculated at the critical section in the tooth root area and subsequently the bending strength geometry factor (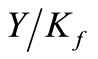 ) is determined. Tooth dimensions are shown in Figure 4 used in the calculation of the tooth form factor (
) is determined. Tooth dimensions are shown in Figure 4 used in the calculation of the tooth form factor ( ). This factor considers the influence of shape of tooth at the critical tooth-root stress. This shape is defined in computational procedure by the parameters of the critical section:
). This factor considers the influence of shape of tooth at the critical tooth-root stress. This shape is defined in computational procedure by the parameters of the critical section:
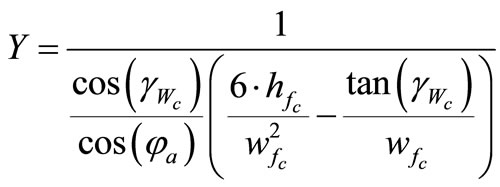 (12)
(12)
where the operating pressure angle 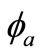 can be found as follows:
can be found as follows:
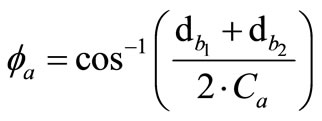 (13)
(13)
The direction angle of the critical tooth force 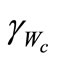 can be found by the following equation:
can be found by the following equation:
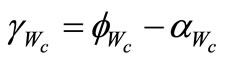 (14)
(14)
The stress correction factor 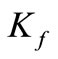 considers the complex stress state at tooth root and stress concentration caused by the fillet. It is calculated based on the work of Dolan and Broghamer [16]. They developed the following stress correction factor curve fit relation:
considers the complex stress state at tooth root and stress concentration caused by the fillet. It is calculated based on the work of Dolan and Broghamer [16]. They developed the following stress correction factor curve fit relation:
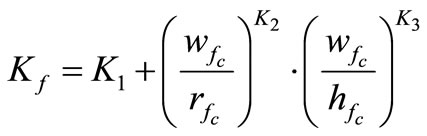 (15)
(15)
From a curve fit of the experimental data of Dolan and Broghamer in their initial photoelastic experiments, AGMA gives the following values for the constants, (K1, K2, K3) in terms of the pitch circle pressure angle,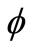 :
:
 (16)
(16)
where 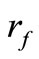 is the fillet radius of curvature, and is given by
is the fillet radius of curvature, and is given by
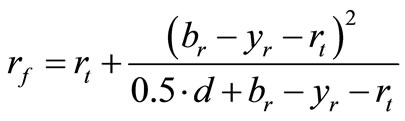 (17)
(17)
The bending strength geometry factor 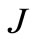 is calculated from the following equation:
is calculated from the following equation:
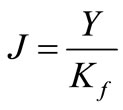 (18)
(18)
This factor reflects the increase in the local stresses due to sharp changes in geometry at the critical section and directly will affect the bending strength under repeated loading. If the cutter parameters are chosen to generate
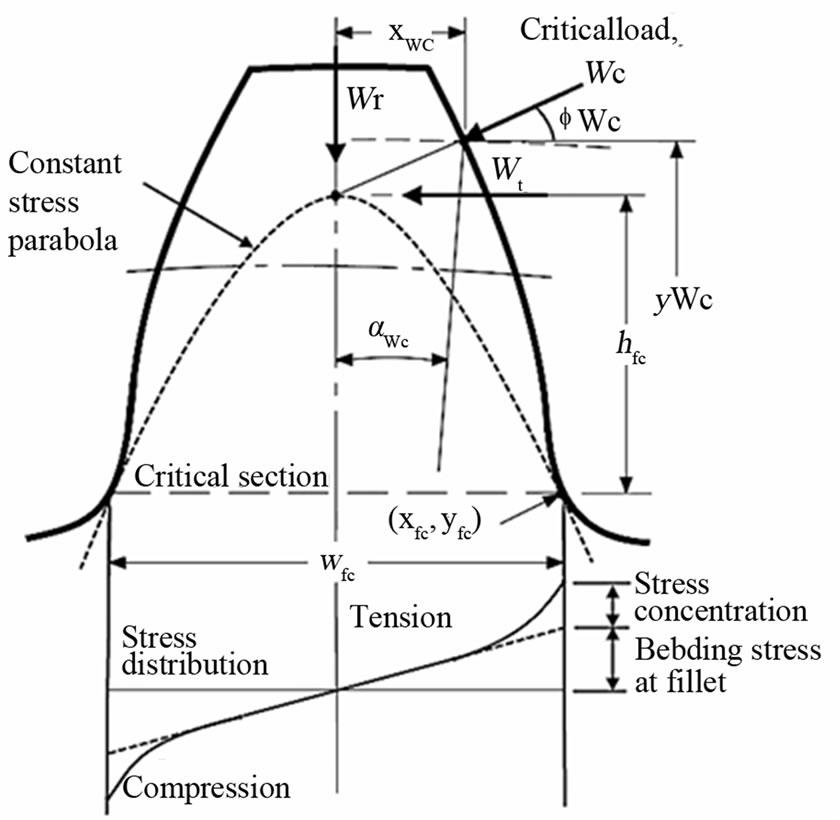
Figure 4. Data for combined tensile stress calculation at the critical fillet section.
the involute flank profile to satisfy certain operation conditions, the fillet profile is an outcome of the cutter motion that will also affect the tooth root strength. Therefore, bending stress reduction achieved by such fillet profile improvement differs and greatly depends on the cutter tip radius or gear tooth parameters. The calculation procedure described above is integrated into the developed gear program [17-19]. It functions as a complete gear design tool according to the relevant standard (AGMA), presenting a comprehensive set of calculations associated with geometry of involute gears and design of the internal and external of the gear sets. It provides a 3D export function used with modules that perform sizing calculations for the gear models. At the touch of a button, it then transfers those calculations to the CAD system and generates a 3D model of sized gears. Then, the strength calculation according to AGMA can be carried out very easily and quickly for comparative calculations. The developed gear program allows for parametric and automatic generation of well-shaped finite element meshes for 2D and 3D gear models with consideration to proper node and element numbering and required tooth fillet profile, as shown in Figure 5.
Consequently, the developed gear program can calculate and provide proper design parameters to establish Probabilistic Design Analysis (PDA) to predict the effect of the trochoid fillet conditions on the reliability of the gear system. With PDA, much more can be done than just predicting reliability after a design is formulated. PDA will allow us to see how variations in material properties, variations in dimensions and variations in the operating environment affect the mean life of the gear pair.

Figure 5. Integrated gear design analysis tools.
3. Development of a Probabilistic Gear Design Approach
The design of the mechanical system requires the assurance of its reliability and quality. Variations and uncertainties in the inputs and properties of the mechanical system (e.g. dimensions, material properties, errors associated with the simulation tools, etc.) may lead to large variations in the performance characteristics of the system and a high chance of failure. Uncertainties in the system characteristics prevent such assurances from being given with absolute certainty. One common approach is to quantify the reliability of performance, or risk of failure, in probabilistic terms [20]. A probabilistic approach, which requires knowledge of the nominal loads and strengths as well as the statistical variations in each, allows the designer to assess the reliability of survival of the mechanical system [21,22].
3.1. Stress-Strength Interference (SSI) Theory
The SSI theory has been used to take into account variations in the operating load and strength of the mechanical system [23] that are distributed about a mean value and which may change with time in service operation owing to degradation. If the probability density function curves for both strength and load are shown to interfere, as shown in Figure 6, then the shaded area where the curves interfere is an indication that the component will fail, because the stress exceeds its strength.
Mathematically, the SSI theory presents the failure probability of the system  as the probability that the stress exceeds the strength.
as the probability that the stress exceeds the strength.
 (19)
(19)
The reliability (R) is the probability that the stress is less than the allowable strength:
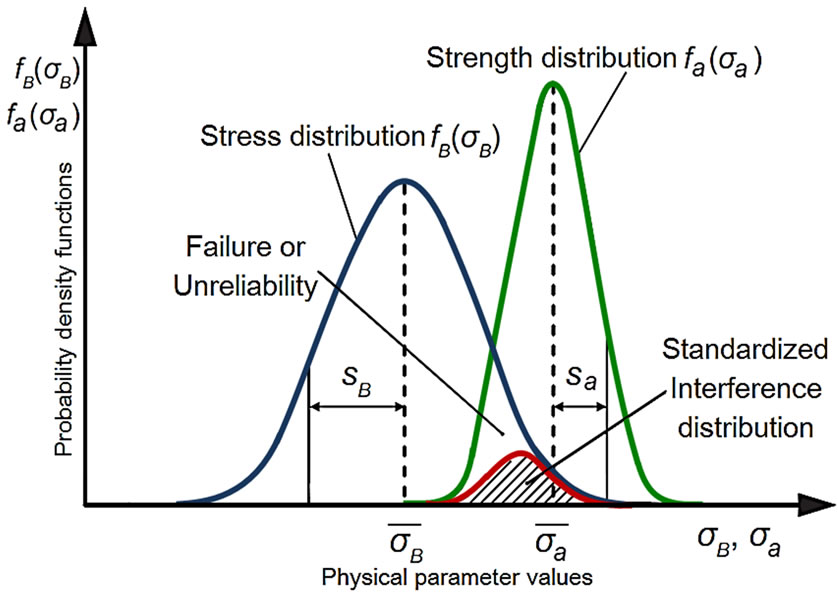
Figure 6. Stress and strength interference theory diagram.
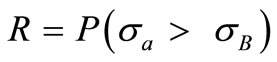 (20)
(20)
Reliability (R) of a component can be calculated, if the density functions for the allowable strength fa(sa) and the actual stress fB(sB) are known. The random variable (U) is a measurement for the distance between the actual stress and the allowable strength:
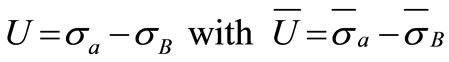 (21)
(21)
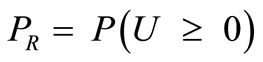 is the probability that: U ≥ 0 the reliability.
is the probability that: U ≥ 0 the reliability.
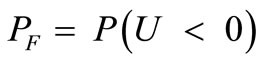 is the probability that U < 0: the failure probability.
is the probability that U < 0: the failure probability.
If the random variables stress 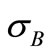 and allowable strength
and allowable strength 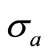 are assumed to be normally distributed due to their numerable random influences, then along with the parameters mean and statistical spread,
are assumed to be normally distributed due to their numerable random influences, then along with the parameters mean and statistical spread,  ,
, 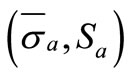 the density function of a normal distributed stress can be determined as follows:
the density function of a normal distributed stress can be determined as follows:
 (22)
(22)
The density function of the allowable strength can be determined in the same way. The random variable (U) is, likewise, normally distributed. The unreliability of failure for the interference area of the two distributions can be calculated using the following equation:
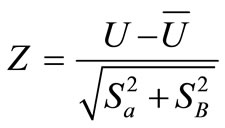 (23)
(23)
Then, the reliability can be simply calculated from the normal distribution function (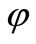 ):
):
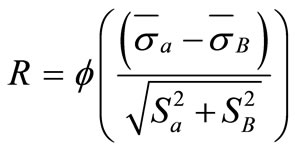 (24)
(24)
3.2. Application of the SSI Theory
In this section, we discuss an application of probabilistic modelling and analysis during the gear design process. Current gear design analysis methods do not directly account for the probabilistic nature of most input parameters. The result of treating parameters such as material properties, geometry, environment, and loads as solely determined (deterministic) values is a design of unknown reliability, or conversely, unknown risk. The minimization of risk of the gear tooth failure has been handled in the design phase by the application of factors of uncertainty and the use of judicious material properties. Probabilistic design analysis can be applied at the various phases of the gear design as long as information is available on the strength (material properties, manufacturing process, etc.) and stress (loads, environments, etc.) parameters.
Figure 7 illustrates this process. The left-hand side shows the input data to determine the applied stress distribution at the critical fillet location that can be found from the applied torque and geometry multiplied by different factors related to the specific application. The result of the gear design is to yield as a tensile bending stress distribution at the critical fillet location, while the other three components in the right-hand side such as material strength, manufacturing process and operations and environment will work together to yield as an adjusting gear material strength distribution. The middle part in the figure shows the output of the process, that being an applied stress and resistive gear strength distribution, with an associated probability of failure. Thus, random design variables affecting both stress and strength are statistically defined. Therefore, the application of this approach allows for calculation of reliability and probability of failure of the gearing system in terms of statistically varying load and strength characteristics, which more nearly model the true situation.
The previous sections indicated that the shape of the tooth fillet is known to be critically important to the tooth bending strength and is the focus of much current gear research. In practice, there are many other parameters that could also affect the bending stress, including gear material properties, applied torque, misalignment, etc. However, these parameters are by nature uncertain due to variability of material properties, tolerances in manufacturing, and the random nature of applied torques. In such case, it is more appropriate to perform uncertainty analysis and evaluate the reliability of gearing system in terms of probability of failure, rather than the maximum value of the bending stress. Among many input parameters that can affect the uncertainty of the tooth bending stress, the shape of the tooth root and the applied
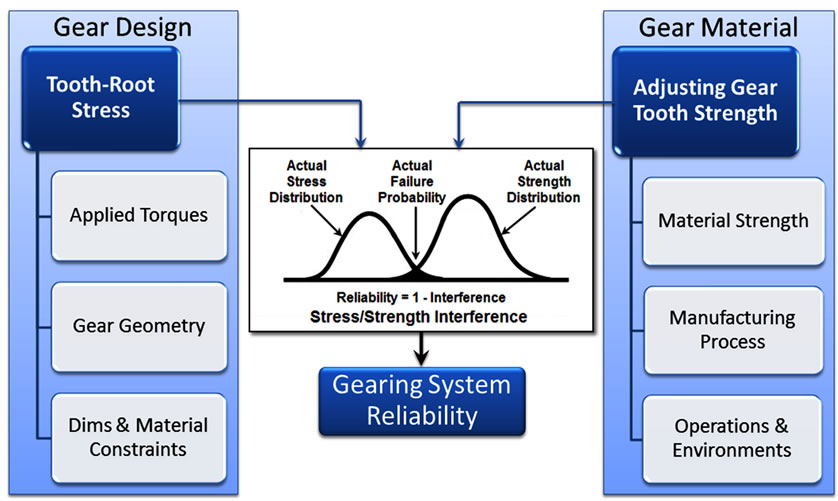
Figure 7. Development of a probabilistic gear design approach.
torque are chosen for the present investigation. As a complementary requirement in the investigation of the uncertainties encountered in the design of gear tooth for bending stress based the SSI theory, the uncertainty of gear material strength is considered. The uncertainty in gear material strength comes from variability in the material structure and machinability. The gear material is chosen to be “Alloy Steel” and a standard deviation based a variation coefficient of ±10% was applied to be able to reflect variability in gear material strength. The capability and simplicity of the normal distribution make it the best choice for representing the variability in gear material strength.
For this proposed analysis, a probabilistic analysis algorithm is developed to interface with the CAD-Integrated analysis tools (see Figure 5) so that the analysis output can be directly fed to the probabilistic program (Minitab Statistical Software [23]) and vice-versa. The main idea is to integrate the probability of applied stress and material strength over the root region where stress exceeds the strength. The result of this integration is to determine the gear reliability and probability of failure, as shown in Figure 8. Thereby, the output distributions will be calculated and the realistic system behaviour can be extracted from these output distributions. To get accurate output distributions, Monte Carlo simulation (MCS) was used to generate a large number of sample points in order to estimate the statistical probability of gear tooth bending stress and strength.
To examine how the tooth-root geometry influences the gear tooth strength, four gear sets with different root geometries (see Figure 3) that are generated by different tip radius of the hobbing cutter have been considered as the test gears. Each test gear has module 3 mm, pressure angle 20 degrees, number of teeth 20 and the same material. The analysis was conducted at a constant gear rotational speed of 1500 rpm and at different applied torque levels ranging between 10 - 35 N-m. Nominal tooth-root stress is produced at the tooth root when the gear pair is loaded by the applied torque. Figure 9 shows the histogram of the distribution density function and the probability occurrence of the tooth bending stress when
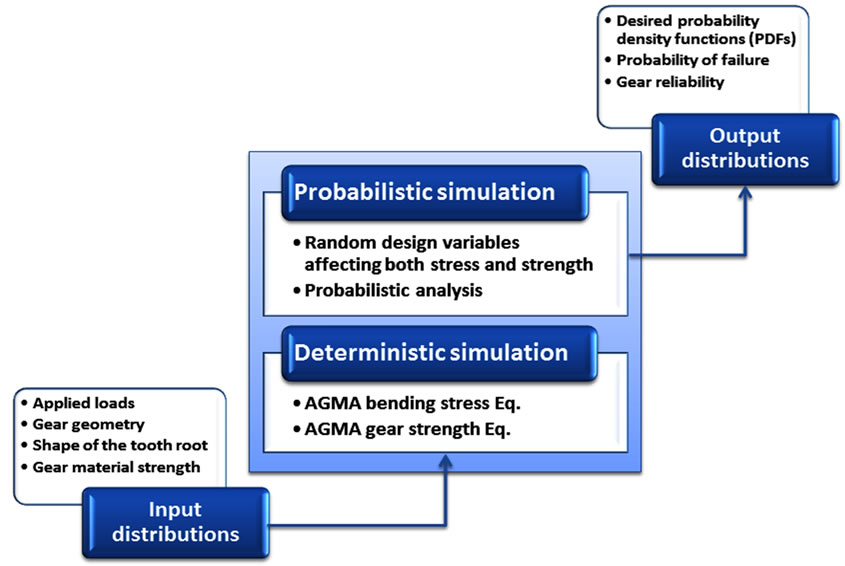
Figure 8. Integrate probabilistic and deterministic gear design analysis.
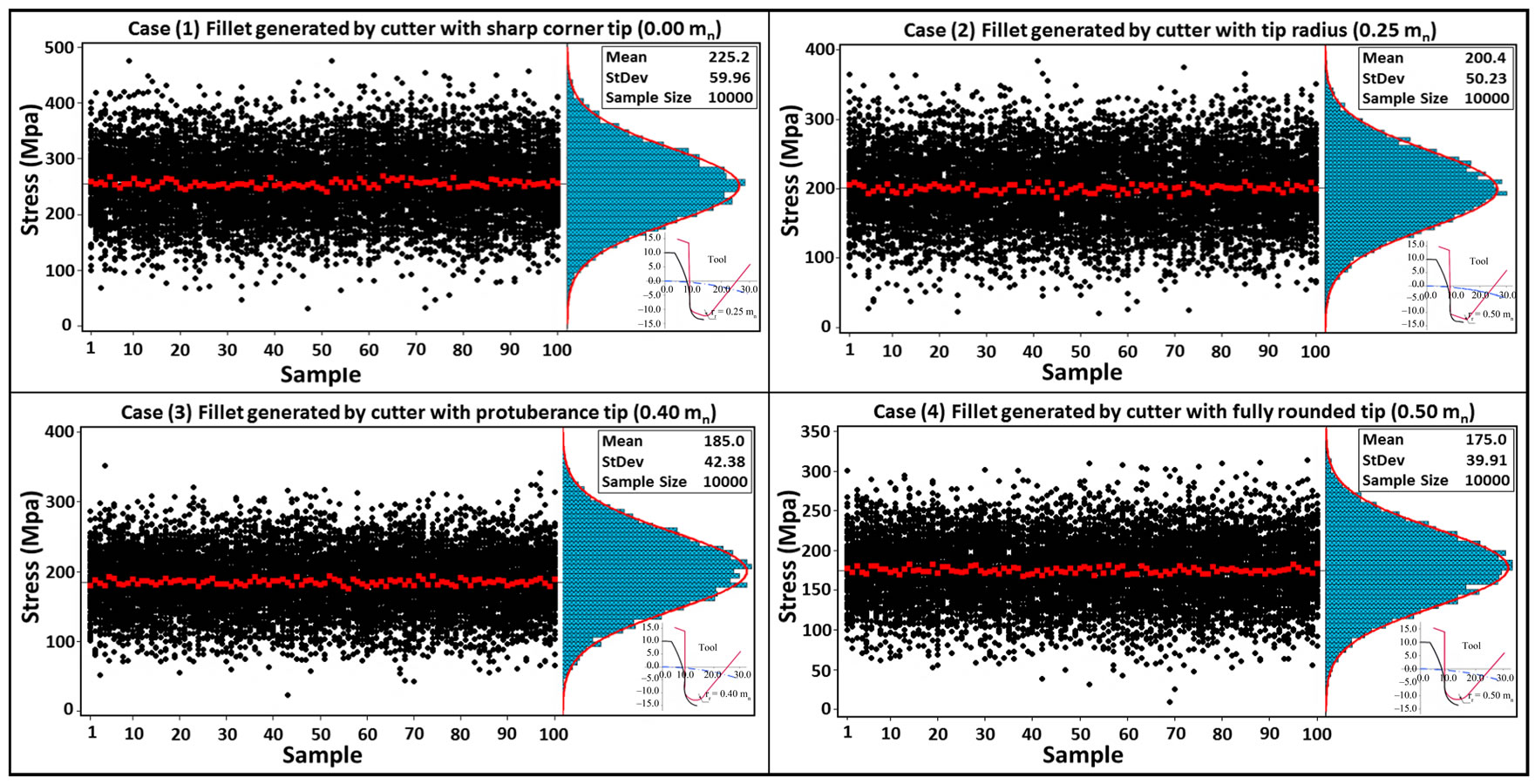
Figure 9. Histograms of the distribution density functions and probability occurrences of the tooth bending stresses for the four case.
generating random values (the sample size is 10,000) of the tooth bending stresses for the four cases, as well as the curve corresponding to the analytical description of the same density function. Case (1) is showing the data of the generated fillet by cutter with the sharp corner tips. It symmetrically distributed with a central tendency about the mean stress of 255 MPa. A normal curve is superimposed over the histogram showing the distribution symmetry and good fit. The dispersion of the histogram data bins are also indicating the variability in stress values experienced at this particular root radius. The run chart on the left side of the graph of case (1) is showing data dispersion of the sample about the mean, it has been noticed that the highest stress values can reach to 480 MPa. In case (2), the mean stress value reduced to 200 MPa and the highest stress value is about 380 MPa. For the tip with protuberance, case (3), an improvement in data clustering about the mean (185 MPa) with high stress around (320 MPa) is noticed compared to the two previous cases. In the fully rounded corner tip radius of the cutter, case (4), the stress results showed less variability about the mean stress (175 MPa) with the highest stress around 300 MPa.
The tooth bending stress distribution for each case is represented graphically against the strength of the gear material distribution based the principal of the SSI theory, as shown in Figure 10. SSI diagram for the stress/strength distributions. According to the interference area between the stress and strength distribution curves, case (1) is showing the highest interference area which indicates more stress points are exceeding the allowable strength distribution, hence reducing reliability and increasing failure probability. The probability of failure in case (1) is found to be about 8.23%. On the other hand, case (4) is showing less interference between the two distributions which enhances the gear reliability and reduces the chances of sudden failing due to high bending stress. The probability of failure in case (4) is found to be about 0.1%.
According to Equation (23), the area of interference between each normally distributed stress case and the normally distributed strength can be calculated to define the unreliability of failure (Z) for each case, as shown in Table 1. Then, the reliability of each case can be determined by subtracting the failure area from the total area under the curve which is 1 (see Equation (24)).
Figure 11 shows the cumulative density functions of the tooth bending stress distributions calculated for the different four cases that described above. From the figure, we see that the probability of getting higher stresses increases as the decreasing in the value of the tip radius of the cutter. The figure also shows the tooth bending stress range for the case (4) is less than the other cases which indicates less stress variability will be experienced at this particular case. According to Figure 11, at 80% sample percentile of the stress occurrence, case (4) provides higher resistance to the bending breakage compared with the rest three cases.
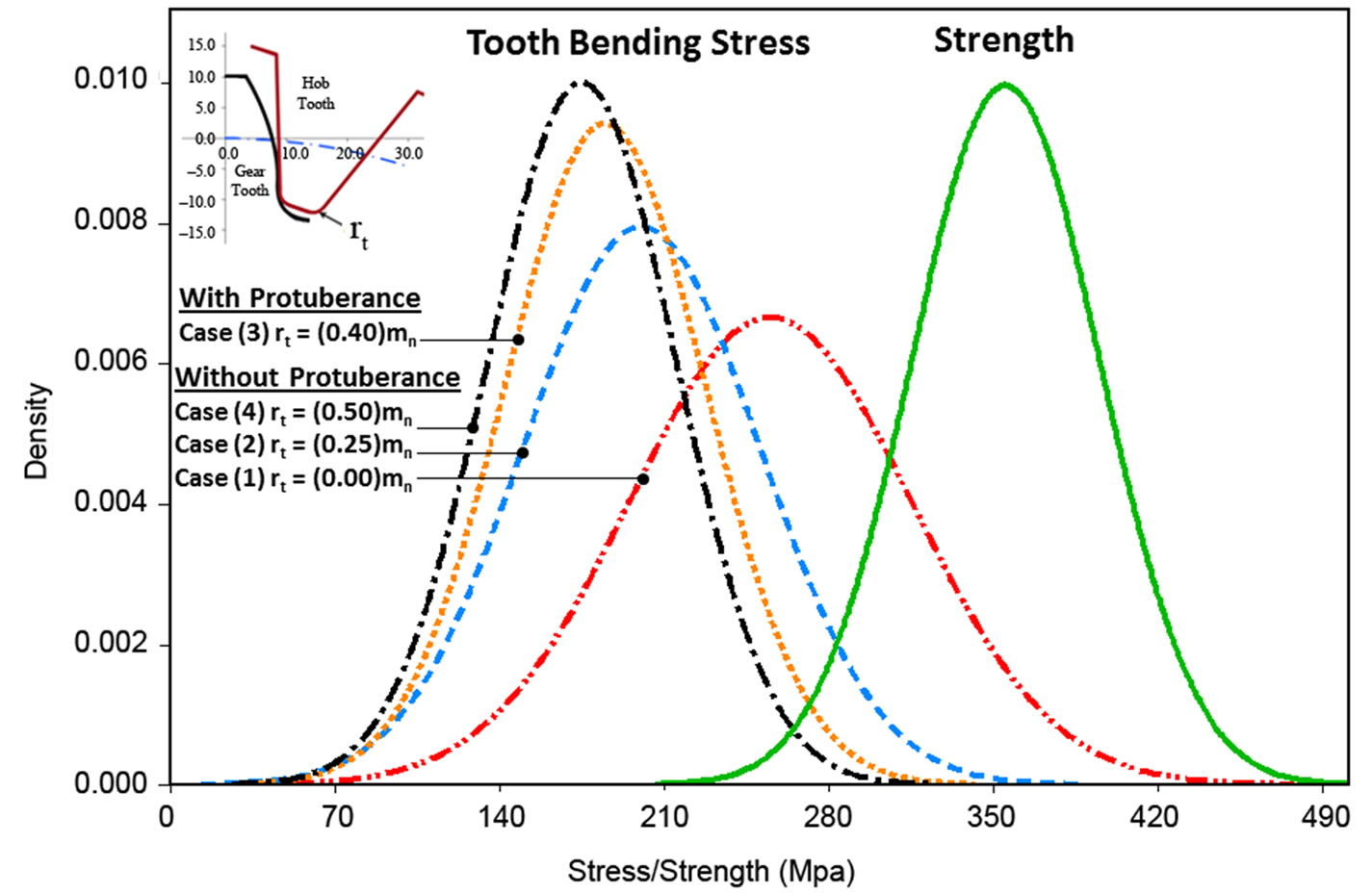
Figure 10. SSI diagram for the stress/strength distributions.
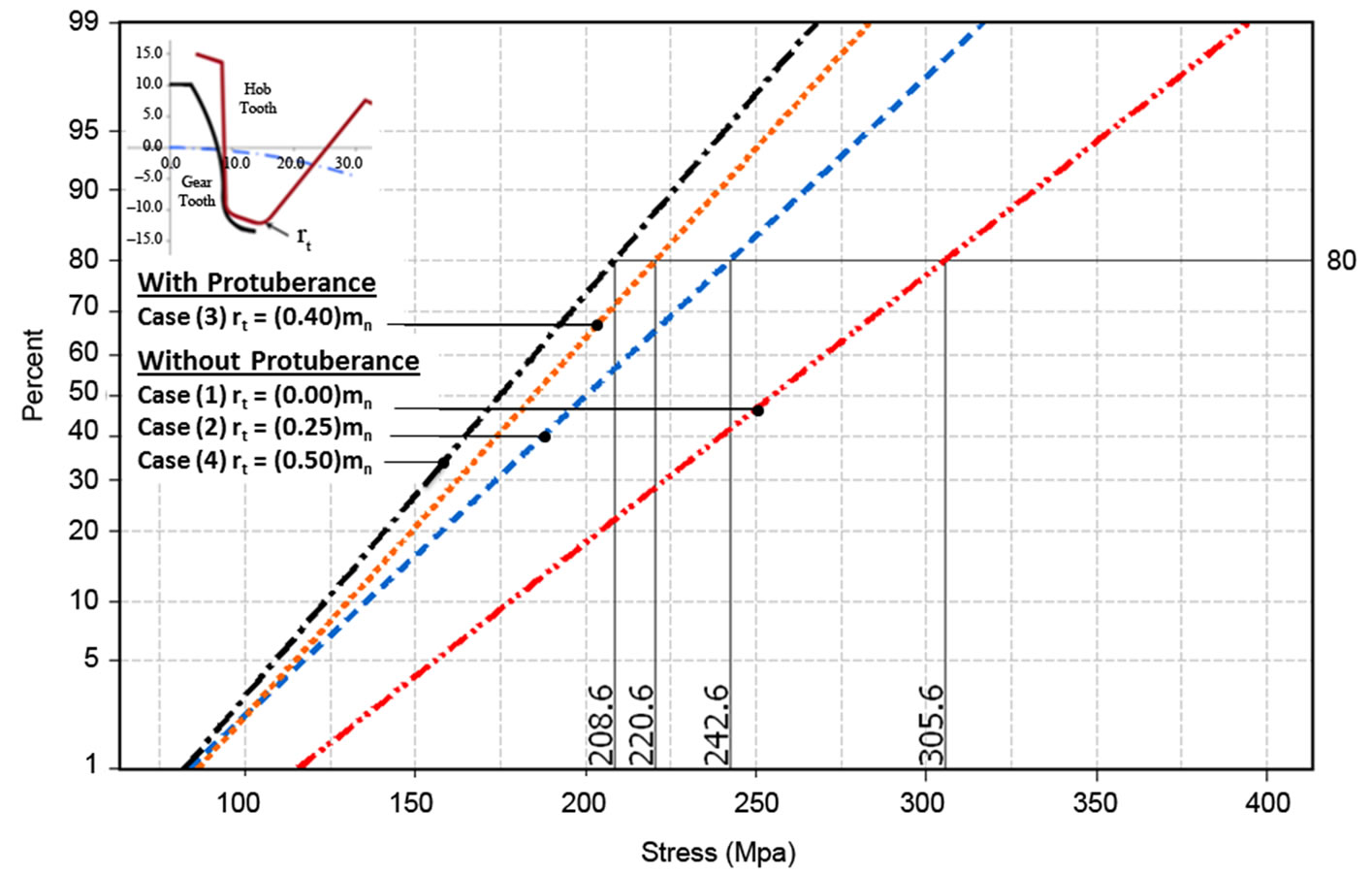
Figure 11. Cumulative density functions of the tooth bending stress dis-tributions.
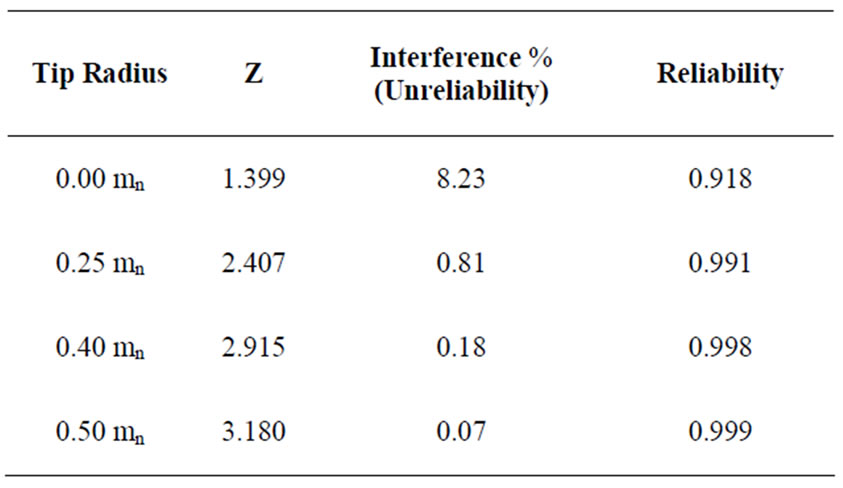
Table 1. Reliability assessment based graphically representtation of statis-tical data for the four cases.
4. FEM-Based Verification Approach
Finite Element Method (FEM) is used to verify the accuracy of the deterministic and probabilistic stress results at the root fillet. The advantage of using FEM is that it can accurately consider the effect of detailed geometry, as well as complex loading conditions. In order to examine precisely the influence of root fillet contour in the gear tooth strength, as shown in Figure 12, the FEM code that was developed for this analysis is split into three functions, each of which serves its own purpose in defining parameters, creating the model, performing analysis, and extracting analysis results.
• The first function defines all variables that are required in constructing the gear geometries, material properties and applied loading conditions. Since all construction processes are parameterized, four different gear sets can be easily constructed by modifying parameters in this function.
• The second function consists of the commands that build a three-dimensional solid model, including only three teeth and generate a finite element mesh by using the automatic mesh generation functionality. Only three teeth are modeled because of periodic symmetry, which will significantly reduce the computational analysis times required to perform finite element analysis of the model. This process is repeated for the pinion and gear to build a gear set assembly. During the real operation, the tip-load condition is not being the worst load because in this condition another pair of teeth will be in contact. Examination of run-in teeth reveals that the heaviest loads occur near the middle of the teeth carrying the full load, that is, at a point where another pair of teeth is on the edge of coming into contact. When a single tooth carries the full load, it has been generally accepted that the maximum tensile bending stress occurs at the highest point of the single-tooth contact (HPSTC). Contact between the gear and pinion is established by defining contact elements on the flank of the gear teeth and target elements on the flank of the pinion teeth. A tangential distributed load is applied uniformly on the pinion surface. Both the gear and pinion are pinned at the center, but is allowed to pinion to rotate and the gear is fixed. The fixed displacement constraint is applied on the boundary surface of the gear and the radial constraint is defined on the boundary surface of the pinion.
• The third function performs postprocessing, which extracts output results such as deformed shapes, normal stresses at the root fillet, and contact pressures. Figure 12 shows the distributions of the effective stresses along the tooth line passing through critical sections in various FEM models of spur gears and along fillet in various transversal sections. To obtain the results of the analysis, maximum principal stresses were searched at every calculation case near the tooth root fillet area to compare with the results calculated by the probabilistic design method.
Figure 13 shows the distribution of the effective stresses along the fillet in various transversal sections corresponding to the four cases discussed in Figure 12. Comparison of these cases indicates that bending stress distribution increases with the root fillet that is generated by small cutter tip radius as in case (1) and the effective stresses for the four cases calculated by FEM are closer
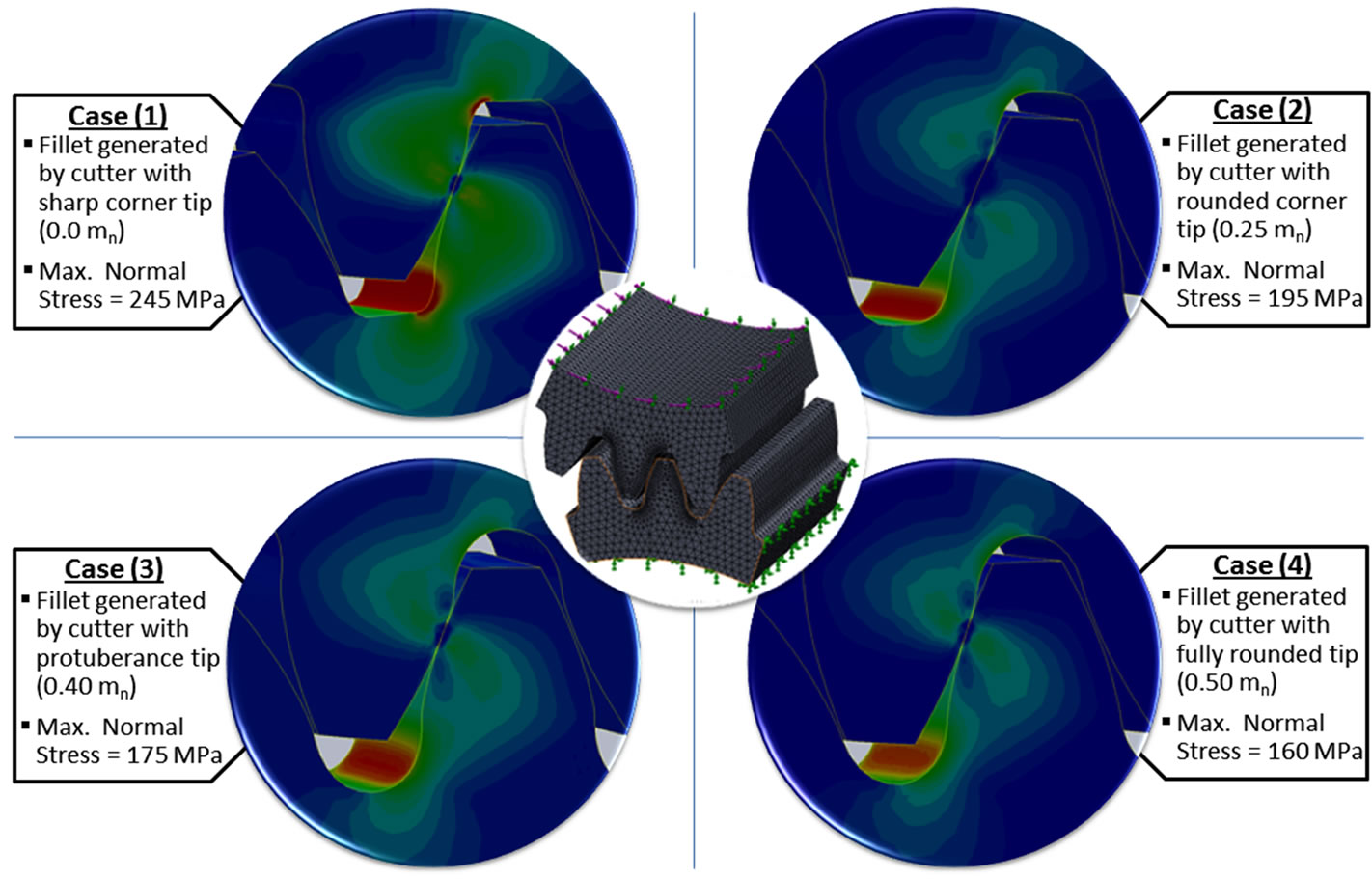
Figure 12. FEM model and tensile bending stress contours for four cases of different fillet profiles.

Figure 13. Comparison of effective normal stress distributions along tooth face width and fillet profiles for four cases (3D and 2D plots).
to those obtained by the probabilistic design method. The 2D chart shows the average of the bending stress distribution along the different fillet profiles for the four cases. The bending stress distribution for the case (4) is much more uniform than the other three cases. Other cases have the significantly greater maximum stresses that are sharply concentrated. The chart also indicates that as the fillet profile changes the position of critical point on the fillet contour for each case is being determined by the maximum tensile bending stress. Generally, this study investigated comparatively larger root fillet within the case (4), which results in notable stress reduction.
5. Conclusions
A reliable approach was developed to evaluate the gear tooth reliability by the bending strength criterion and integrated into the developed gear program as a probabilistic design tool. The SSI theory as a probabilistic design tool was applied to examine the influence of root fillet contour on the gear tooth strength for four gear sets with different fillet profiles. This approach is implemented upfront during the gear design phase to assist the designer in making decisions on the best balanced design with respect to several design criteria.
Thus, uncertainty analysis is performed to estimate the probabilistic distribution of the tooth root stress. Consideration the SSI failure probability calculation for bending breakage, has shown that the shortest portion of the fillet profile in case (1) provided the highest interference area which indicates more stress points are exceeding the allowable strength distribution, hence reducing reliability with about 9% probability of failure. The analysis of the mean nominal bending strength revealed that the fillet profile generated by the fully rounded tip radius in case (4) had the highest strength compared with the rest cases.
FEM of tooth-root strength is performed for each modeled gear set to verify the accuracy of the deterministic and probabilistic stress results at the root fillet. There is strong agreement between the probabilistic analysis and FEM’s results across a range of different fillet profiles; this confirms the fillet generated by the full tip radius in case (4) has the lowest maximum bending stress, which is uniformly distributed along the large portion of the fillet profile. Other fillet profiles have significantly greater maximum stresses that are sharply concentrated.
Understanding the relationship between process variables uncertainties with the gear performance and safety is accomplished. This approach helps making the decision regarding the most reliable design by quantifying the impact of stress and strength variations during the gear design stage.
6. REFERENCES
- A. Vlahinos, S. Kelkar, S. Reh, R. Secaur and S. Pliz, “Reliability Based Optimization within the CAD Environment,” 2002. http://www.aes.nu/publications/2002-ReliabilityBasdOptimiz-bmx-ANSYS.pdf
- G. Cooper and G. Thompson, “Concept Design and Reliability,” Acta Polytechnica, Vol. 42, No. 2, 2002, pp. 3-12.
- O. P. Yadav, S. S. Bhamareb and A. Rathoreb, “Reliability-Based Robust Design Optimization: A Multi-Objective Framework Using Hybrid Quality Loss Function,” Quality and Reliability Engineering International Journal, Vol. 26, No. 1, 2010, pp. 27-41. doi:10.1002/qre.1027
- X. He and S. O. Oyadiji, “A Study of Practical Reliability Estimation Method for a Gear Reduction Unit,” IEEE SMC’99 Conference Proceedings, Vol. 1, 1999, pp. 948- 953.
- X. Du and W. Chen, “Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design,” Journal of Mechanical Design, Vol. 126, No. 2, 2004, pp. 225-233. doi:10.1115/1.1649968
- D. P. Townsend, “Dudley’s Gear Handbook,” McGrawHill, New York, 1992.
- A. Kawalec, J. Wiktor and D. Ceglarek, “Comparative Analysis of Tooth-Root Strength Using ISO and AGMA Standards in Spur and Helical Gears with FEM-Based Verification,” Journal of Mechanical Design, Vol. 128, No. 3, 2006, pp. 1141-1158. doi:10.1115/1.2214735
- A. L. Kapelevich and T. M. McNamara, “Direct Gear Design for Automotive Applications,” SAE World Congress & Exhibition, Detroit, 2005.
- S. Xiaogen and D. R. Houser, “Characteristics of Trochoids and Their Application to Determining Gear Teeth Fillet Shapes,” Journal of Mechanism and Machine Theory, Vol. 35, No. 2, 2000, pp. 291-304. doi:10.1016/S0094-114X(99)00004-X
- V. B. Math and S. Chand, “An Approach to the Determination of Spur Gear Tooth Root Fillet,” Journal of Mechanical Design, Vol. 126, No. 2, 2004, pp. 336-340. doi:10.1115/1.1666891
- J. Brauer, “Analytical Geometry of Straight Conical Involute Gears,” Journal of Mechanism and Machine Theory, Vol. 37, No. 1, 2002, pp. 127-141. doi:10.1016/S0094-114X(01)00062-3
- M. Savage, K. L. Rubadeux and H. H. Coe, “Bending Strength Model for Internal Spur Gear Teeth,” NASA Lewis Research Center, Cleveland, 1995.
- AGMA 930-A05, “Calculated Bending Load Capacity of Powder Metallurgy (P/M) External Spur Gears,” American Gear Manufacturers Association, Alexandria, 2005.
- AGMA Information Sheet 908-B89, “Geometry Factors for Determining the Pitting Resistance and Bending Strength of Spur, Helical and Herringbone Gear Teeth,” American Gear Manufacturers Association, Alexandria, 1989.
- K. Stoker, A. Chaudhuri and N. H. Kim, “Safety of Spur Gear Design under Non-Ideal Conditions with Uncertainty,” Proceedings of the ASME 2010 IDETC/CIE, Montreal, 15-18 August 2010, pp. 1-11.
- T. J. Dolan and E. L. Broghame, “A Photoelastic Study of Stresses in Gear Tooth Fillets,” University of Illinois Engineering Experiment Station Bulletin 335, 1942.
- E. S. Aziz and C. Chassapis, “Knowledge-Based Geometry Generation for Spur and Helical Gears,” Concurrent Engineering: Research & Applications (CERA) Journal, Vol. 10, No. 3, 2002, pp. 251-261.
- E. S. Aziz and C. Chassapis, “An Intelligent Design System for Agile Design and Manufacturing of Mechanical Transmission Systems,” The 9th International ASME Power Transmission and Gearing Conference, Chicago, 2-6 September 2003.
- E. S. Aziz and C. Chassapis, “A Decision-Making Framework Model for Design and Manufacturing of Mechanical Transmission System Development,” Engineering with Computers Journal, Vol. 21, No. 2, 2005, pp. 164- 176. doi:10.1007/s00366-005-0320-z
- B. Bertsche, “Reliability in Automotive and Mechanical Engineering: Determination of Component and System Reliability,” VDI-Buch, Springer-Verlag, Berlin, 2008.
- R. C. Kuczera and Z. P. Mourelatos, “On Estimating the Reliability of Multiple Failure Region Problems Using Approximate Metamodels,” Journal of Mechanical Design, Vol. 131, No. 12, 2009, pp. 1-11. doi:10.1115/1.4000326
- E. G. Haugen, “Probabilistic Mechanical Design,” John Wiley and Sons, New York, 1980.
- P. Martin, “A Review of Mechanical Reliability,” Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, Vol. 212, No. 4, 1998, pp. 281-287. doi:10.1243/0954408981529484

