Engineering
Vol. 4 No. 1 (2012) , Article ID: 17092 , 5 pages DOI:10.4236/eng.2012.41001
Computational Analysis of Flow Field on the Propulsion Nozzle of a Micro-Turbojet Engine
1Engineering Aeronautics CFD Laboratory, School Higher of Engineering Mechanical and Electrical, National Polytechnic Institute, San José Ticoman, México
2Applied Thermal and Hydraulic Engineering Laboratory, SEPI-ESIME-IPN Unidad Profesional “Adolfo Lopez Mateos”, Lindavista, México
Email: mtv49@yahoo.com, jgarrido@ipn.mx
Received June 24, 2011; revised August 30, 2011; accepted September 5, 2011
Keywords: Propulsion Nozzle; Model Transport Equation; Numerical Simulation; Small Micro Turbine
ABSTRACT
The purpose of this paper is to analyze the flow field on the propulsion nozzle of a micro-turbojet engine in function of the velocity. The 2D axisymmetric numerical simulation was made by using commercial software FLUENT®. A microturbojet engine was also employed for this study and it has the following characteristics: 100 N thrust, 130,000 rpm, mass flow rate 0.2650 kg/s, weight 1.2 kg. This engine is operating in Mexico city under the following conditions: P0, 78,000 Pa T0, 300 K, πc, 2.1 and a turbine entry temperature of 1000 K; it is considered that the nozzle is not choked. For this study, the viscous standard k-ε model, a semi-empirical model based on transport model equations for the turbulent kinetic energy (k) and its dissipation rate (e), is used. The transport model equation for k is derived from the exact equation, while the transport model equation for (e) is obtained by using physical reasoning and bears resemblance to its mathematically exact counter-part. The employed grids are structured and the boundary conditions are obtained from a thermodynamic analysis. The results that are obtained show an increment of the velocity of 6.25% to the exit propulsion nozzle.
1. Introduction
Before the 90’s, the airplane modeling made of jet engine with a Ducted Fan, engines that basically ware a piston engine connected to a propeller of several blades as is shown in Figure 1. This engine produced a thrust of about 53 N at 30,000 RPM. The model had a jet engine appearance, however, during operation; the engine sound was like a common piston engine [1-3].
In the early 90’s the first micro turbojet engine designed for airplane modeling purposes called JPX appeared. It was built by a French company. JPX-240 en-

Figure 1. Engine type ducted fan.
gine produced a thrust up to 40 N. The last model was JPX-260P engine that produced a thrust up to 62.3 N with a radial turbine as is depicted in Figure 2. JPX engine represented a great advance for the airplane modeling world because of the technological development. At


Figure 2. Micro-turbojet with turbine radial.
the same time, in the middle of 1994, Jesús Artes, Kurt Schreckling and Thomas Kamps developed the first micro-turbojet engine with an axial turbine, the KJ-66. This engine started giving a thrust of 44.14 N, and these days it produces 92.3 N to 128,000 RPM. Because of these great results other companies like RAM in USA, Simjet in Denmark, Jet-Cat in Germany, adopted this technology and they are also developing their own. Currently the only company that is building micro-jet engines with its own technology is AMT in Holland and USA. At the moment, these engines have higher demands in Europe, Australia, USA and Venezuela just to mention some countries. Nowadays, in Mexico City, Felipe Nieto along with Jesus Artes is manufacturing some components employing some of these high-tech engines.
2. Numerical Formulation
A two-dimensional axisymmetric numerical simulation of the complete steady flow on the propulsion nozzle of a micro-turbojet engine has been carried out. Calculations have been performed with a commercial software FLUENT®. This code uses the finite volume method and the Navier-Stokes equations are solved on a structured grid. The code solves the fully compressible Navier-Stokes equations with implicit formulation.
Turbulence is simulated with the standard k-ε (two equations) model. The pressure-velocity coupling is calculated through the SIMPLE algorithm, second order upwind discretization for the momentum and turbulence kinetic energy [4-7].
2.1. The Standard k-ε Model
The standard k-ε model is a semi-empirical model based on transport model equations for the turbulent kinetic energy (k) and its dissipation rate (e). The transport model equation for k is derived from the exact equation, while the transport model equation for e is obtained by using physical reasoning and bears little resemblance to its mathematically exact counterpart. In the derivation of the k-e model, it was assumed that the flow is fully turbulent.
2.2. Transport Equations for the Standard k-ε Model
The turbulent kinetic energy (k), and its rate of dissipation (e), are obtained from the following transport equation:
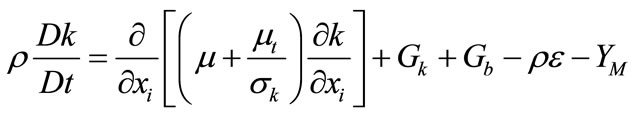 (1)
(1)

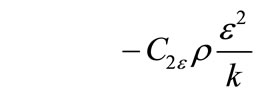 (2)
(2)
In these Equations (1) and (2), 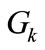 represents the generation of turbulent kinetic energy due to the mean velocity gradients,
represents the generation of turbulent kinetic energy due to the mean velocity gradients, 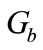 is the generation of the turbulent kinetic energy due to buoyancy,
is the generation of the turbulent kinetic energy due to buoyancy,  represents the contributions of the fluctuating dilatation in compressible turbulence to the overall dissipation rate,
represents the contributions of the fluctuating dilatation in compressible turbulence to the overall dissipation rate, 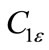 ,
, 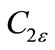 and
and 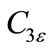 are constants,
are constants,  and
and  are the turbulent Prandtl numbers for
are the turbulent Prandtl numbers for 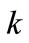 and
and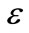 , respectively.
, respectively.
2.3. The Turbulent Viscosity
The “eddy” or turbulent viscosity (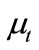 ), is computed by combining
), is computed by combining 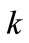 and
and 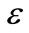 as follows:
as follows:
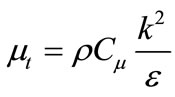 (3)
(3)
where 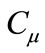 is a constant.
is a constant.
2.4. Model Constants
The model constants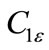 ,
,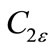 ,
,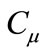 ,
,  and
and 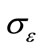 have the following default values [7]:
have the following default values [7]:
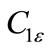 = 1.44,
= 1.44,  =1.92,
=1.92, 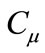 = 0.99,
= 0.99, 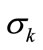 = 1.0,
= 1.0,  = 1.3.
= 1.3.
The degree to which e is affected by the buoyancy is determined by the constant , it is not specified, but it is instead calculated according to the following relation.
, it is not specified, but it is instead calculated according to the following relation.
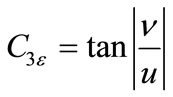 (4)
(4)
where n the component of the flow velocity is parallel to the gravitational vector and u is the component of the flow velocity perpendicular to the gravitational vector. In this way, 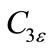 will become 1 for buoyant shear layer for which the main flow direction is aligned with the direction of gravity. For buoyant shear layers that are perpendicular to the gravitational vector,
will become 1 for buoyant shear layer for which the main flow direction is aligned with the direction of gravity. For buoyant shear layers that are perpendicular to the gravitational vector, 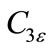 will be zero.
will be zero.
3. Configuration and Grid Generation
Figures 3 and 4 show the geometry and the dimensions of the propulsion nozzle with the external and internal cones.
In this study the boundary conditions are obtained by a thermodynamic analysis, in which the micro-turbojet engine is being operated in Mexico City under the following conditions: P0, 78,000 Pa T0, 300 K, 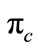 , 2.1 and a turbine entry temperature of 1000 K, it is considered that the nozzle is not choked.
, 2.1 and a turbine entry temperature of 1000 K, it is considered that the nozzle is not choked.
Grid Generation and Boundary Conditions
Figure 5 shows the structured grids (control volume).
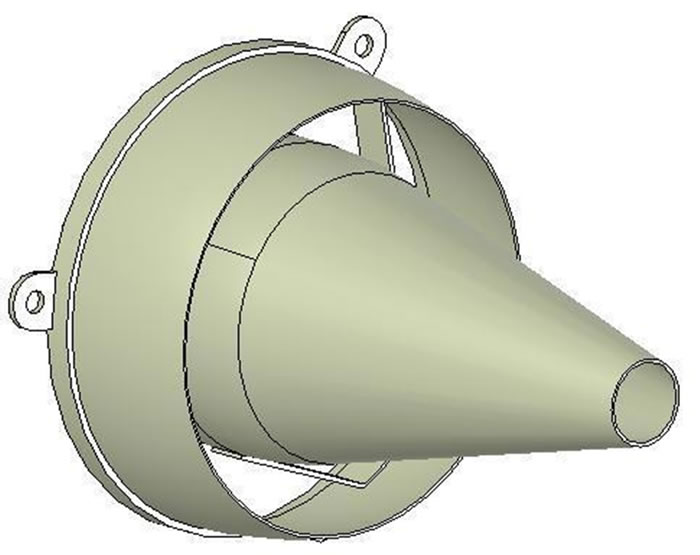
Figure 3. Geometry of the propulsion nozzle 3D.
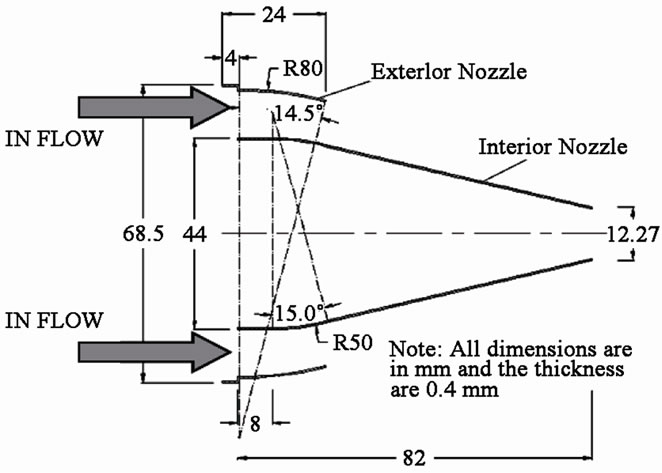
Figure 4. Dimensions of the propulsion nozzle 2D.
For this study, the grids have an ellipse quarter form, their length is 4L and their exterior radio is 3R. Figure 5(a) shows the grid of the original propulsion nozzle and
 (a)
(a)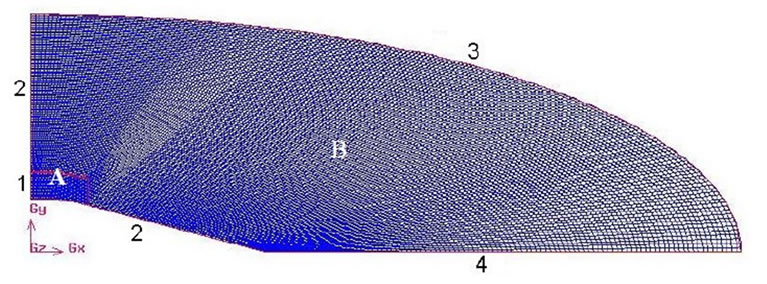 (b)
(b)
Figure 5. Structured grids (a) original propulsion nozzle and (b) modified propulsion nozzle.
it is formed by three structured grid; grid (A) has 1330 quadrilaterals cells, the (B) has 950 and the (C) has 4910 with a total of 7190 quadrilateral cells. Figure 5(b) shows the grid of the modified propulsion nozzle and it is formed by two structure grids; grid (A) has 800 and the grid (B) has 18,100 cells with a total of 18,900 quadrilaterals cells. Table 1 shows the following boundary and initial conditions.
4. Results
The obtained results of the original propulsion nozzle in velocity contours fields form are shown in Figure 6, where it is observed a discontinuity in the flow, mainly in the tail nozzle due to the presence of the adverse velocity gradients and a fall in the momentum of the flow. The velocity in this point is 334.98 m/s. Figure 7 shows a close-up of the velocity field at the exit of the nozzle, where it is observed some vectors columns. In the first one, the adverse velocity vectors appear totally devel-
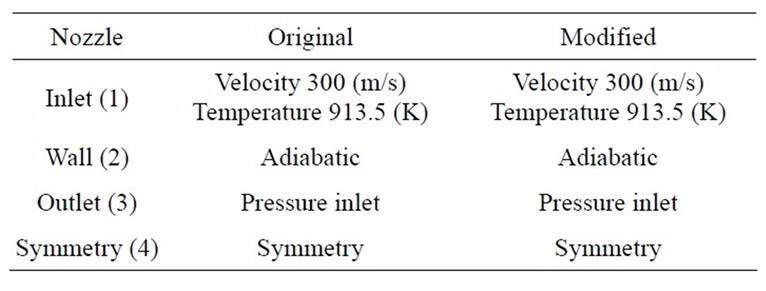
Table 1. Boundary and initial conditions for the nozzles.
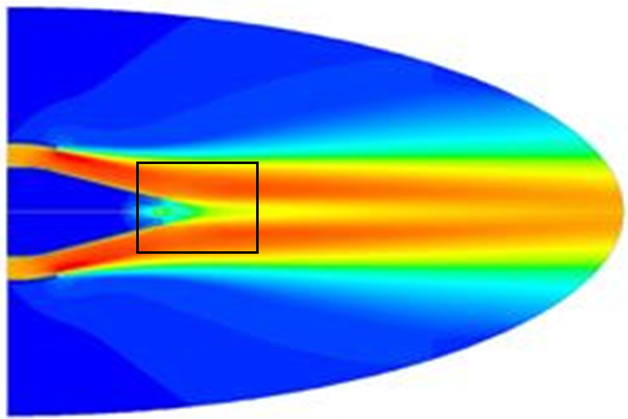
Figure 6. Contours velocity field in original nozzle.

Figure 7. Close-up of adverse velocity gradients.
oped and in the upper and below side it can be seen the formation of the flow eddies. In the second column, the formation adverse velocity vectors begin, and in the next columns it is observed the continuity of the flow with below momentum. Figure 8 shows the modified propulsion nozzle.
Figure 9 shows the obtained results of the modified propulsion nozzle where it is observed the continuity in the flow principally in the tail nozzle and a continuation in the momentum. The velocity at this point is 335.47 m/s. Figure 10 shows a close-up of the velocity vectors field at the exit of the propulsion nozzle, where it is observed the continuity in the momentum of flow.
The Table 2 values were obtained from the grid (A) of
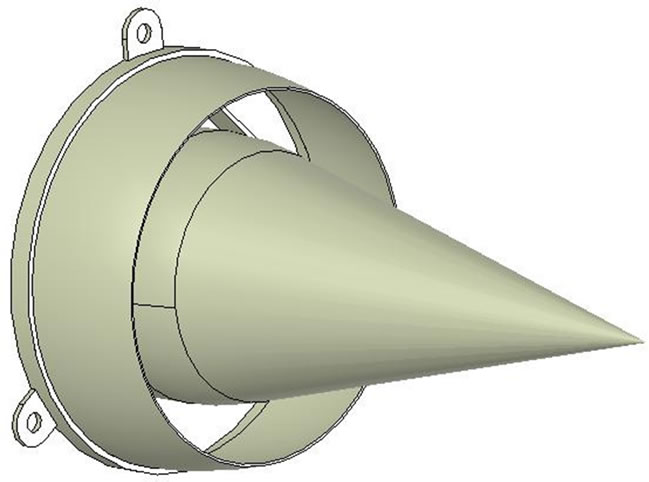
Figure 8. Modified propulsion nozzle.
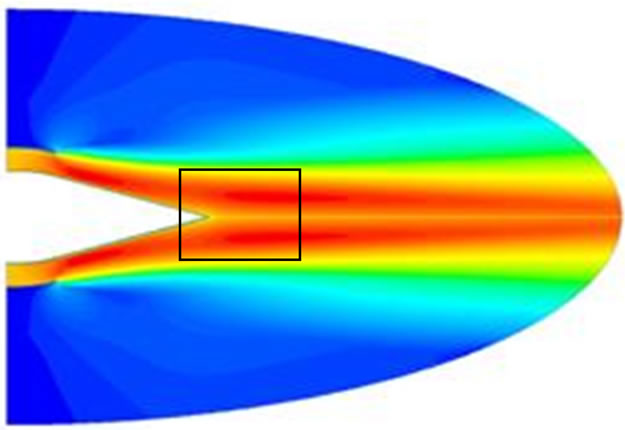
Figure 9. Contours velocity field in modified nozzle.
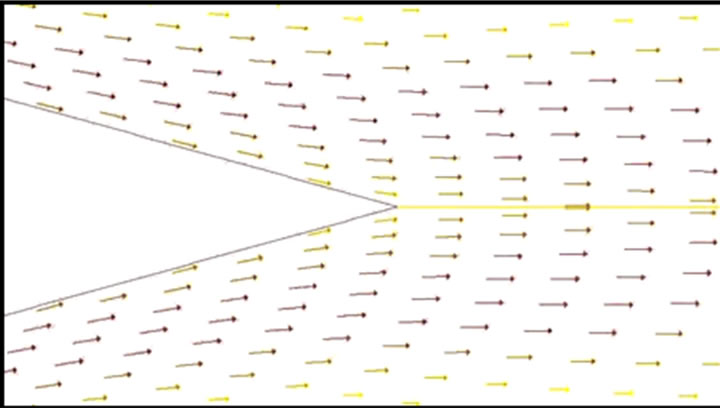
Figure 10. Close-up in the tail modified propulsion nozzle.
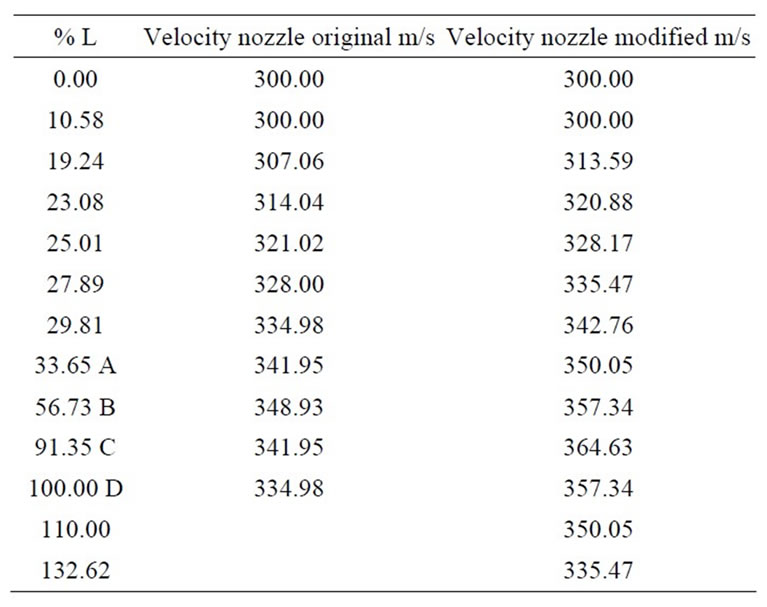
Table 2. Shows the velocity values for the two nozzles in function of the % L.
Figure 5(a), where x takes values from i = 0 to i = 95 and y take values in j = 9. The same procedure is done for Figure 5(b) in the modified propulsion nozzle. Figure 11 shows the values of the velocity increments for each nozzle in function of % L. In this graphic it is observed that in point A there is an increment in the velocity of 2.31%, in point B 2.53%, in point C 6.22% and in point D there is an increment of 6.25%. In the original propulsion nozzle, the maxim value of velocity is reached in point B, and after it falls, due to the presence of adverse velocity gradients in the exit nozzle tail. On the other hand, in the modified propulsion nozzle, the velocity reaches its maxim in D, and after it falls [8-12].
5. Conclusions
The results obtained in this study show the performance of the velocity field in the nozzles that were analyzed. Mainly, in the original propulsion nozzle, the presence of adverse velocity gradients in the exit provokes a decrease in the momentum of the flow, causing a falling in the velocity field. In the modified nozzle, the enlargement of the tail in the internal cone means a total increment of 6.25% in the velocity and continuity in the flow without
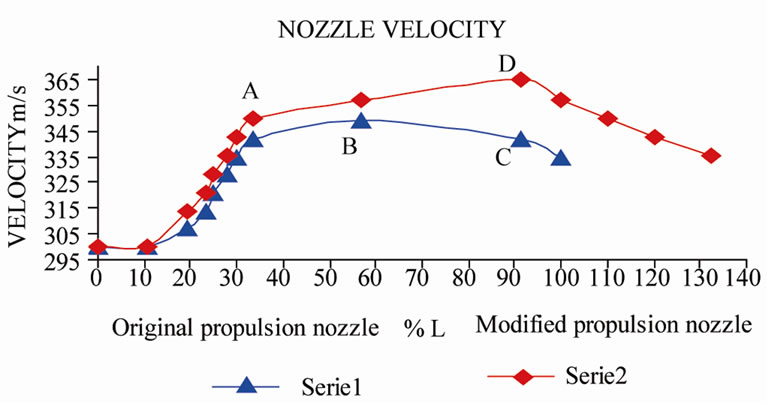
Figure 11. Velocity nozzle vs % L.
the loss of the momentum in the flow.
REFERENCES
- D. J. Mattingly, “Elements of Gas Turbine Propulsion,” McGraw-Hill, Inc., New York, 1996.
- M. P. Boyce, “Gas Turbine Engineering Handbook,” Gulf Publishing Company, Houston, 1982.
- T. J. Chung, “Computational Fluid Dynamics,” Cambridge University Press, Cambridge, 2002.
- J. M. Steven and A. W. Kenrick, “Computational Analyses of Propulsion Aeroacoustics for Mixed Flow Nozzle Pylon Installation at Takeoff,” NASA/C-2001-211056, September 2001. http://aeroelasticity.larc.nasa.gov/wp-content/uploads/2010/08/NASA-CR-2001-211056.pdf
- R. H. Thomas, K. S. Kinzie and S. P. Pao, “Computational Analysis of a Pylon-Chevron Core Nozzle Interaction,” AIAA Paper 2001-2185, 2001.
- D. C. Kenzakowski, J. Shipman and S. M. Dash, “Turbulence Model Study of Laboratory Jets with Mixing Enhancements for Noise Reduction,” AIAA Paper 200- 0219-2002.
- B. E. Launder and D. B. Spalding, “Lectures in Mathematical Models of Turbulence,” Academic Press, London, 1972.
- S. Sarkar and L. Balakrishnan, “Application of a ReynoldsStress Turbulence Model to the Compressible Shear Layer,” ICASE Report 90-18, NASA CR 182002, 1990.
- L. L. Baxter, “Turbulent Transport of Particles,” PhD Thesis, Brigham Young University, Provo, 1989.
- A. Brandt, “Multi-Level Adaptive Computations in Fluid Dynamics,” Technical Report AIAA-79-1455, AIAA, Williamsburg, 1979.
- J. L. Ferzieger and M. Peric, “Computational Methods for Fluid Dynamics,” Springer-Verlag, Heidelberg, 1996.
- B. Stephen, “Pope Turbulent Flows,” Cambridge University Press, Cambridge, 2000.
Nomenclature
C: constant
G: generation of kinetic energy
L: length [m]
P0: stagnation pressure [Pa]
R: radio [m]
T0: stagnation temperature [T]
T: temperature [T]
Y: contribution fluctuating dilatation
 : rate of dissipation [m2/s3]
: rate of dissipation [m2/s3]
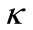 : turbulent kinetic energy [m2/s2]
: turbulent kinetic energy [m2/s2]
 : viscosity [kg/m-s ]
: viscosity [kg/m-s ]
 : compressor pressure ratio
: compressor pressure ratio
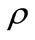 : density [kg/m3]
: density [kg/m3]
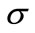 : turbulent Prandtl number
: turbulent Prandtl number
B: buoyancy
M: fluctuating dilatation
T: turbulent

