Engineering
Vol. 3 No. 10 (2011) , Article ID: 8077 , 5 pages DOI:10.4236/eng.2011.310120
A Simplified Procedure for Predicting the Ultimate Strength of Beam-Column Channel Sections
OB Engineering Ltd., 151 Chapalina Mews SE, Calgary, Canada
E-mail: obedair@gmail.com
Received April 11, 2011; revised May 16, 2011; accepted May 30, 2011
Keywords: Channels, Steel Design, Cold Formed Sections
ABSTRACT
A design procedure is presented to estimate the load carrying capacity of beam-column channel sections. A reduced cross-section is used to compensate for the reduction in the post-buckling stiffness. The non-linear stress distribution acting on the entire channel width is replaced by simplified linear distributions. Using this simplified concept, the maximum stress in the post-buckling state, is assumed to be carried entirely by both edges while the central region of the channel remains unstressed. Thus a fraction of the channel section is considered in resisting the applied loading. This approximation enables the structural engineer to deal with a simplified stress distribution to compute the ultimate strength instead of the non-linear one.
1. Introduction
Channel sections are extensively used in steel construction. The design of these members depends upon their industrial application. Channel sections are commonly used in light steel construction, such as false ceilings, catwalks, lighting partitions, curtain walls, cable trays, … etc. In this case excessive deformation is not favourable because the members support structures sensitive to deflection. Therefore, buckling would be the governing limit state. Channel sections are also used in the design of structures subjected to medium loadings, such as purlins, bracings, girts, …etc. This group is suitable for mild post-buckling deflection. Therefore serviceability limit state governs the design. The channel member in this case is braced in the lateral direction at regular intervals in order to reduce the effective length. Channel sections are also used in heavily loaded steel construction. Examples are column studs, primary beams framing, etc. A cost effective procedure is to design these members to accommodate full post-buckling capacity. Therefore, with proper understanding to the structural behaviour, the channel section can be grouped by the fabricators to provide cost-effective products in the marketplace.
The determination of the ultimate strength is a challenging in the design of channel sections. Several investigations were conducted by many researchers to provide understanding to the channel behaviour. Dinis and Camotim [1] presented a numerical study for post-buckling behaviour of simply supported cold-formed lipped channel columns using Finite element Method. Luo [2] presented a study to investigate the stress characteristics of cold-formed thin-walled lipped channels under combined loading. Kolakowski and Kowal-Michalska [3] investigated the influence of the axial extension mode on interactive buckling of thin-walled channel with geometric imperfections subjected to uniform compression. They used simply supported boundary condition. Yao et al. [4] used the finite strip method to study the elastic buckling stress of lipped channel sections. They provided approximate formula for the buckling coefficient using regression analysis procedure. Vraný [5] investigated numerically the loading effect of various restraints on cold-formed C and Z-purlins. Chu, et al. [6] investigated, using the energy method, the influence of cladding restraints on buckling behaviour of purlins. Ren, et al. [7] presented finite element models for analysis of coldformed steel channels subjected to pure bending. Salhab and Wang [8] investigated the behavior of perforated channel studs. The equivalent channel thickness was estimated using FE simulation considering several design variables such as plate depth, thickness, perforation patterns, …etc. A regression equation was proposed to relate the equivalent thickness to these parameters. Yan and Young [9] presented a numerical Finite Element study to investigate buckling of fixed-ended cold-formed steel channel columns with various lip profiles subjected to axial load. Jana and Bhaskar [10] used superposition techniques for buckling analysis of plates under nonuniform compressive stress. Wang, et al. [11] employed the differential quadrature method to compute the buckling load of plates under non-uniform compression. Bedair [12] investigated the influence of the lip and flange sizes on the buckling and post-buckling strength of cold-formed channel section under uniform compression. It was shown that the web buckling stress is largely affected by the sizes of the channel components and is not constant as assumed by the North American steel codes [13-15]. A noticeable increase in the post-buckling stiffness of the web and the flange was attained by accounting for the geometric interaction.
Objective of this paper is to provide simplified design procedure to estimate the load carrying capacity of thin walled beam-column channel sections. The non-linear stress distribution is approximated by a simplified linear distribution. A reduced cross-section is used to compensate for the reduction in the stiffness in the post-buckling range. This simplified procedure enables the structural engineer to compute the ultimate strength of the channel section and avoid the cost and effort that any numerical non-linear analysis may require.
2. Non-Linear Stress Approximation
Consider typical beam-column channel section of length (L), width (b) and thickness (t) as shown in Figure 1. The origin is chosen at the centerline of the channel. A schematic of the typical non-linear stress distribution across the channel width is shown by the colored shaded area. For slender channels the buckling stress (σcr) is less than the yield stress (σY). In the post-buckling state, the longitudinal membrane stresses (σx) shift from the center of the web and concentrate at the longitudinal edges. If the applied load is uniform compression, the maximum edge stresses are equal (σmax1 = σmax2). With increasing load beyond buckling, the longitudinal edges carry, by equal amounts, most of the load compared to the center of the web. If the applied load is not uniform, the stresses at the edges are not equal (i.e. σmax1 ≠ σmax2). Their magnitudes depend on the distribution of the applied load. Therefore, the stress, in the post-buckling range, carried by each edge differs and one anticipates that one edge will yield before the other.
The non-linear stress distribution acting on the entire width of the web can be replaced by equivalent uniform blocks distributed over two reduced effective widths (be1 and be2). By using this simplified concept, the maximum stress in the post-buckling state, is assumed to be carried entirely by the longitudinal strips while the central region of the plate remains unstressed. Thus only a fraction of the channel width is used in the design.
Therefore, the non-uniform stress distribution shown schematically in Figure 1, can be approxi-mated by two strips of width, (be1) and (be2 ), such that
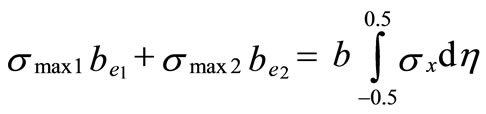 (1)
(1)
where η and ξ are non-dimensional parameters = y/b and x/L, respectively. (σmax1) and (σmax2) are the stresses at η = –0.5 and 0.5 respectively, and (be1) and (be2) are their corresponding effective widths. The right block can be assumed to carry the load from the center line of the channel, η = 0, to the edge η = 0.5, i.e.
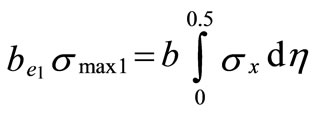 (2)
(2)
Similarly, the left block is assumed to carry the load from η = 0 to the other edge, η = –1/2, i.e.
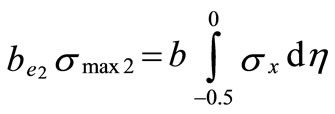 (3)
(3)
Note that (be1) and (be2) should satisfy the following inequality;
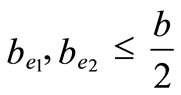 (4)
(4)
In some loading scenarios, the resulting non-linear stress distribution has the profile shown in Figure 2. The maximum stress within –0.5 ≤ η ≤ 0 is not located at the
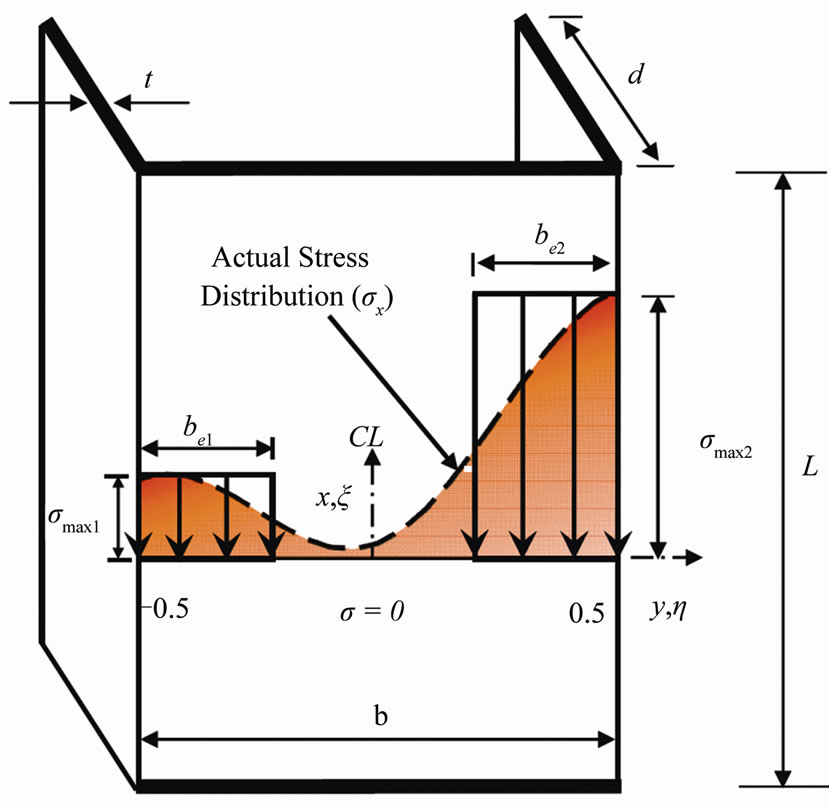
Figure 1. Longitudinal stress approximation.
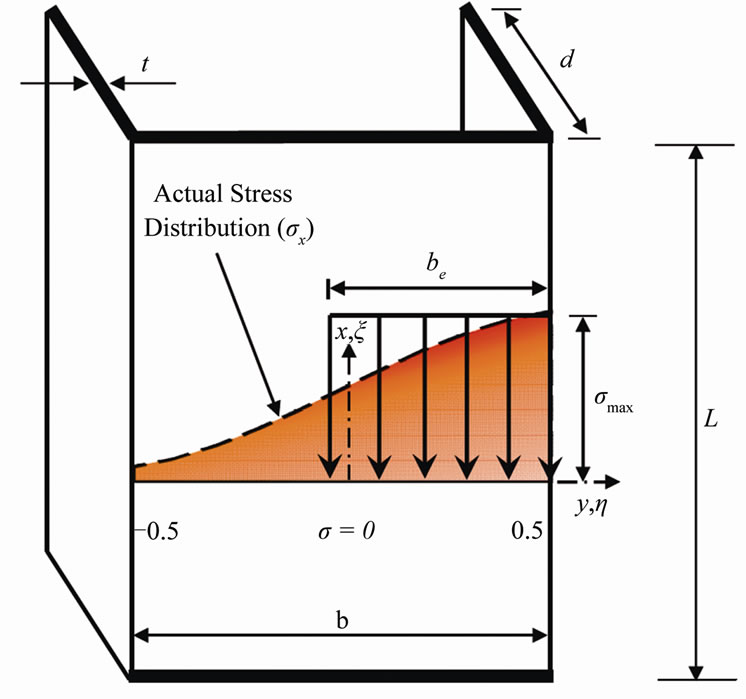
Figure 2. Alternative stress approximation.
left edge of the web, η = –0.5. It is located in the vicinity of the channel center line. A reasonable approximation of (be) in this case, is to assume that the stress is completely carried by the right edge, η = 0.5, as shown in Figure 2. In this case Equation (2) modifies to;
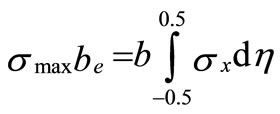 (5)
(5)
The determination of the stress distribution (σx) can then be obtained by solving the following coupled compatibility and equilibrium differential
 (6)
(6)
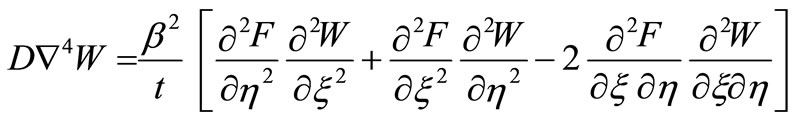 (7)
(7)
where
 (8)
(8)
where β is the plate aspect ratio = L/b, W is the total out of plane deflection, E is Young’s modulus, D is the plate flexural rigidity given by Et3/12(1 − v2) and F is the stress function defined as;
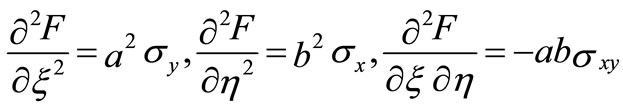 (9)
(9)
3. Approximate Solutions for Beam-Columns
For beam-column channel section subjected to combined compression and major axis bending (clockwise), the applied loading varies linearly in the transverse direction and can be expressed as;
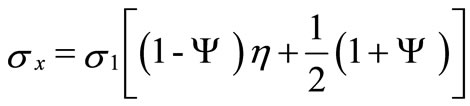 (10)
(10)
where (Ψ) is the stress gradient coefficient that relates the applied stresses at the channel edges. In this case (s1) is the compressive stress at the heavily loaded edge (η = 0.5). The applied stress at the opposite channel edge (η = –0.5) equals (Ψs1). The post-buckling stress distribution is obtained by solving the coupled Equations (6) and (7), and is expressed as;
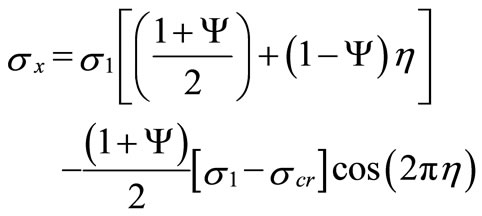 (11)
(11)
By substituting the values [σmax1, σmax2], into Equations (2) and (3) the width of each block [be1, be2] will have the following expressions;
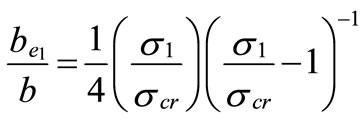 (13)
(13)
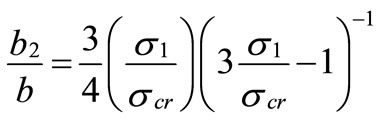 (14)
(14)
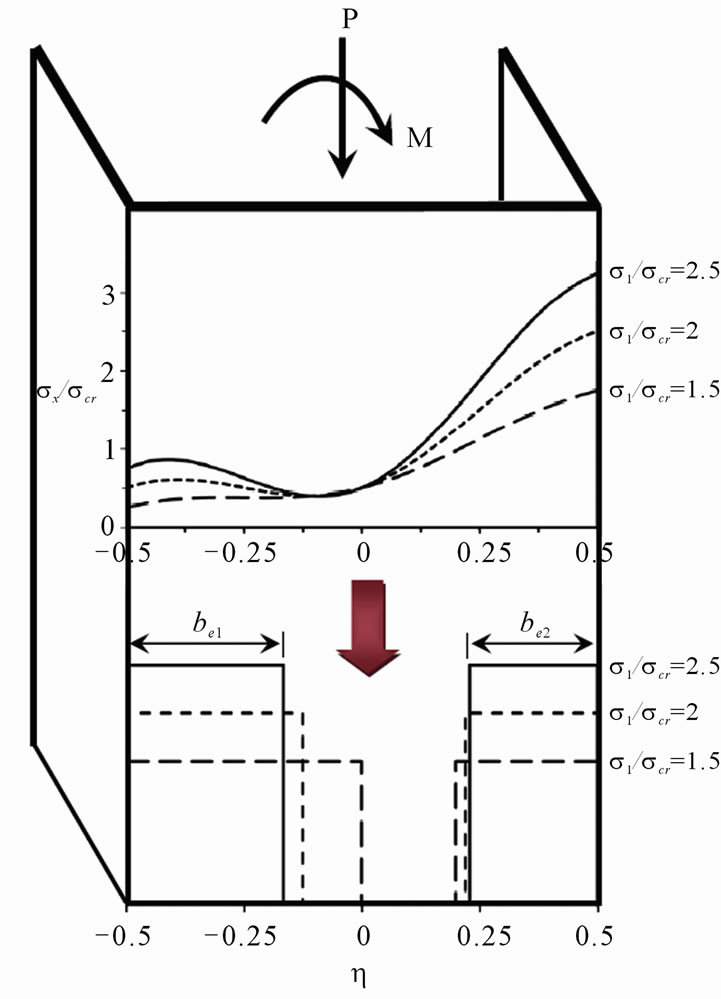
Figure 3. Stress and effective width variation (Ψ = 0).
Figure 3 illustrates the approximation procedure for the channel section subjected to the triangular loading (i.e., Ψ = 0). Top diagram shows the non-linear postbuckling stress distributions and the lower sketch shows the corresponding reduced widths (be1) and (be2). Note that the legends used in both diagrams are identical. For example, the solid curve represents stress ratio 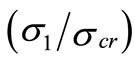 = 2.5. The dashed and long dashed curves represent stress ratios
= 2.5. The dashed and long dashed curves represent stress ratios 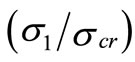 = 2 and 1.5, respectively. It can be observed that by increasing the applied load in the post-buckling state
= 2 and 1.5, respectively. It can be observed that by increasing the applied load in the post-buckling state , the stress shifts from the central part of the channel and concentrates at the edges. The increase of the stresses at the heavily loaded edge is very rapid. The location of the minimum stress for this loading scenario shifts from the center line toward the left edge, η = –0.5 and is located at
, the stress shifts from the central part of the channel and concentrates at the edges. The increase of the stresses at the heavily loaded edge is very rapid. The location of the minimum stress for this loading scenario shifts from the center line toward the left edge, η = –0.5 and is located at
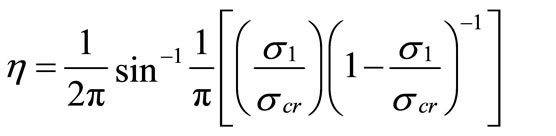 (12)
(12)
It can also be noted that the location of the minimum stress is a function of the post-buckling applied stress ratio, 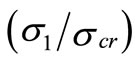 For example when
For example when 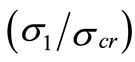 = 2, the minimum stress is located at (η) = –0.1. By increasing this ratio, the minimum stress shifts toward the centerline. By increasing the stress ratio to
= 2, the minimum stress is located at (η) = –0.1. By increasing this ratio, the minimum stress shifts toward the centerline. By increasing the stress ratio to 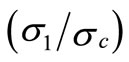 = 3, the location of the minimum stress changes to (η) = –0.08. For
= 3, the location of the minimum stress changes to (η) = –0.08. For 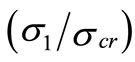 = 4 it further reduces to –0.07, ...etc.
= 4 it further reduces to –0.07, ...etc.
The elastic ultimate strength of the channel can obtained by replacing [σx]max, i.e. [σx]η = 1/2, by the yield stress (σY ) to get;
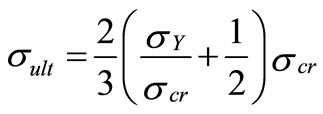 (15)
(15)
Figure 4 shows another example for a channel section with stress gradient ratio (Ψ = 0.4). Top diagram shows the non-linear post-buckling stress distributions and the lower shows the corresponding effective widths. The location of the minimum stress in this case is given by
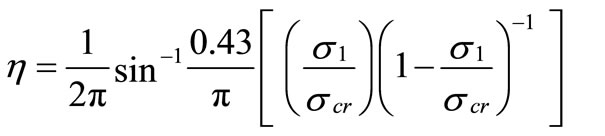 (16)
(16)
The effective width of each block [be1, be2] for this loading condition is given by;
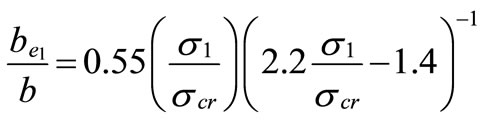 (17)
(17)
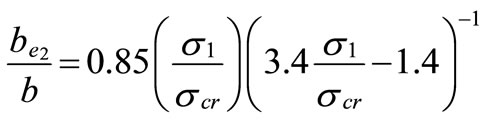 (18)
(18)
The ultimate strength of the channel for this loading condition is given by;
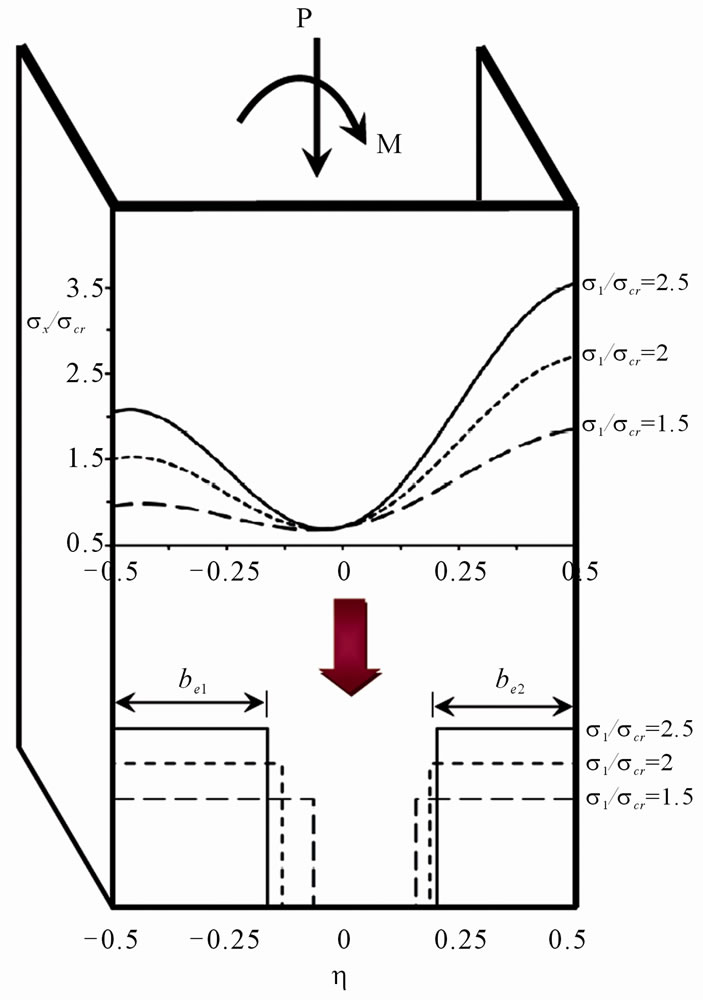
Figure 4. Stress and effective width variation (Ψ = 0.4).
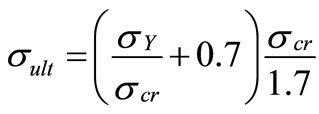 (19)
(19)
The changing mechanisms of the effective widths (be1) and (be2) due to changes in 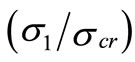 are depicted, in the lower diagram of Figure 4. It can be observed that by increasing
are depicted, in the lower diagram of Figure 4. It can be observed that by increasing 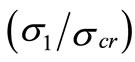 each block gets narrower and higher at almost equal rates until the right block reaches the yield value.
each block gets narrower and higher at almost equal rates until the right block reaches the yield value.
To give examples to the numerical values, by fixing 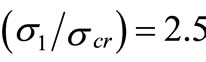 the non-dimensional stress
the non-dimensional stress 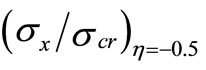 increases from 0.75 at (Ψ) = 0 to 2.05 at (Ψ) = 0.4. By increasing (Ψ) to 0.8,
increases from 0.75 at (Ψ) = 0 to 2.05 at (Ψ) = 0.4. By increasing (Ψ) to 0.8, 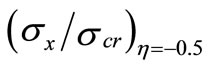 increases to 3.35. When Ψ = 1, the edge stress reaches a value of 4. The non-dimensional stress at the other edge
increases to 3.35. When Ψ = 1, the edge stress reaches a value of 4. The non-dimensional stress at the other edge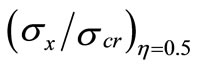 , on the other hand, increases from 3.25 to 3.55 by increasing (Ψ) from 0 to 0.4, then to 3.85 when (Ψ) = 0.8 and reaches 4 when (Ψ) = 1.
, on the other hand, increases from 3.25 to 3.55 by increasing (Ψ) from 0 to 0.4, then to 3.85 when (Ψ) = 0.8 and reaches 4 when (Ψ) = 1.
4. Conclusions
A simplified design procedure is presented to estimate the load carrying capacity of thin walled beam-column channel sections. The non-linear stress distribution acting on the entire channel width was replaced by a simplified linear distribution. A reduced cross-section is then used to compensate for the reduction in the stiffness in the post-buckling range. This approximation enables the structural engineer to deal with a simplified stress distribution to compute the ultimate strength instead of the non-linear one. The sensitivity and mechanics of the reduced channel width to the stress gradient parameter was shown. The resulting analytical expressions have simple forms, suitable for hand-calculation and avoid the cost and effort that any numerical non-linear analysis may require.
5. REFERENCES
- P. B. Dinis and D. Camotim, “Post-Buckling Behaviour and Strength of Cold-Formed Steel Lipped Channel Columns Experiencing Distortional/Global Interaction,” Computers and Structures, Vol. 89, No. 3-4, 2011, pp. 422-434. doi:10.1016/j.compstruc.2010.11.015
- H. Luo, Y. Guo and Y. Xu, “Distortional Buckling of Cold-Formed Thin-Walled Channel Beams in Combined Compression and Minor Axis Bending,” Advanced Materials Research, Vol. 163-167, 2011, pp. 507-510. doi:10.4028/www.scientific.net/AMR.163-167.507
- Z. Kolakowski and K. Kowal-Michalska, “Interactive Buckling Regarding the Axial Extension Mode of a Thin-Walled Channel under Uniform Compression in the First Nonlinear Approximation,” International Journal of Solids and Structures, Vol. 48, No. 1, 2011, pp. 119-125. doi:10.1016/j.ijsolstr.2010.09.010
- X. Yao, Y. Li and Z. Shen, “Load-Carrying Capacity Estimation Methods for Cold-Formed Steel Lipped Channel Member Using Effective Width Method,” Advanced Materials Research, Vol. 163-167, 2011, pp. 90-101. doi:10.4028/www.scientific.net/AMR.163-167.90
- T. Vraný, “Effect of Loading on the Rotational Restraint of Cold-Formed Purlins,” Thin-Walled Structures, Vol. 44, 2006, pp. 1287-1292. doi:10.1016/j.tws.2007.01.004
- X. Chu, J. Rickard and L. Li, “Influence of Lateral Restraint on Lateral-Torsional Buckling of Cold-Formed Steel Purlins,” Thin-Walled Structures, Vol. 43, No. 5, 2005, pp. 800-810. doi:10.1016/j.tws.2004.10.012
- W. Ren, S. Fang and B. Young, “Analysis and Design of Cold-Formed Steel Channels Subjected to Combined Bending and Web Crippling,” Thin-Walled Structures, Vol. 44, No. 3, 2006, pp. 314-320. doi:10.1016/j.tws.2006.03.009
- B. Salhab and Y. Wang, “Equivalent Thickness of ColdFormed Thin-Walled Channel Sections with Perforated Webs under Compression,” Thin-Walled Structures, Vol. 46, No. 7-9, 2008, pp. 823-838. doi:10.1016/j.tws.2008.01.029
- J. Yan and B. Young, “Numerical Investigation of Channel Columns with Complex Stiffeners—Part I: Test Verification” Thin-Walled Structures, Vol. 42, No. 6, 2004, pp. 883-893. doi:10.1016/j.tws.2003.12.002
- P. Jana and K. Bhaskar, “Stability Analysis of Simply-Supported Rectangular Plates under Non-Uniform Uniaxial Compression Using Rigorous and Approximate Plane Stress Solutions,” Thin Walled Structures, Vol. 44, No. 5, 2006, pp. 507-516. doi:10.1016/j.tws.2006.04.009
- X. Wang, X. Wang, and X. Shi, “Differential Quadrature Buckling Analyses of Rectangular Plates Subjected to Non-Uniform Distributed in-Plane Loadings,” Thin Walled Structures, Vol. 44, No. 8, 2006, pp. 837-843. doi:10.1016/j.tws.2006.08.008
- O. Bedair, “A Cost-Effective Design Procedure for ColdFormed Lipped Channels under Uniform Compression,” Thin-Walled Structures, Vol. 47, No. 11, 2009, pp. 1281- 1294. doi:10.1016/j.tws.2009.04.001
- CSA-2001, “Limit State Design of Steel Structures,” Canadian Standard Association CAN/CSA-S16-01, Mississauga, Ontario, 2001.
- CISC-2006, “Handbook of Steel Construction,” Canadian Institute of Steel Construction, Toronto, Ontario, 2006.
- AISC “Steel Construction Manual,” 13th Edition, American Institute of Steel Construction, Chicago, 2005.

