Engineering
Vol. 3 No. 3 (2011) , Article ID: 4139 , 4 pages DOI:10.4236/eng.2011.33023
Mathematical Modelling in Placing of Fresh Concrete
Civil Engineering Department, Niğde University, Niğde, Turkey
E-mail: abilgil@nigde.edu.tr, abilgil@hotmail.com
Received January 18, 2011; revised January 24, 2011; accepted January 29, 2011
Keywords: Fresh Concrete, Flow Concrete, Aggregate Segregation, Mathematical Modelling, Particle Size Distribution
ABSTRACT
The main problem in working with fresh concrete is the aggregate segregation during filling of formwork. The segregation is strongly related to W/C (Water/Cement) ratio. The fresh concrete is usually considered as a Non-Newtonian fluid since it is a mixture of aggregate, cement and water. The flow behavior of the fresh concrete to W/C ratio plays a crucial role in the quality of the high performance concretes by affecting the flow behaviour of the fresh concrete. The aggregates in the fresh concrete usually cause segregation in the final product depending on the flow condition. In this study, the mechanism of segregation in such systems was theoretically investigated. The mould filling of fresh concrete was numerically investigated and aggregates were considered as Lagrangian particles and segregation was identified from trajectories of such particles. It was found that the aggregates were trapped at the dead zones leading to segregation in the system. The particle size and geometry of the mould was found to have significantly affect the segregation in the system.
1. Introduction
Fresh concrete is usually employed to obtain steel reinforced concrete structures. The parameters such as reinforcing steel, mould shape etc. prevent homogenous distribution of aggregates in the structure. Heterogeneous distribution of aggregates also has detrimental effects on the strength of concrete. The excess water in the fresh concrete or higher fluidity is known to be main parameter, leading to segregation, sedimentation and instability of concrete. According to Hoshino [1], due to an interactive action between adjacent solid particles in a dense suspension, segregation of aggregate can lead to sedimentation of unhydrated cement grains and early hydration products in plastic concrete. Khayat and Guizani [2] stated that sedimentation of fines, the segregation of aggregate, and upward migration of bleed water affected surface settlement. Additionally, they stated that bleeding, segregation, and settlement could cause anisotropy in the direction of casting and weaken the interface between the aggregate and cement paste, hence increasing the tendency to develop micro cracking in such regions, resulting a direct implication on permeability, durability, and strength. Soshiroda [3], experimentally determined effects of W/C ratios on the fluidity of the concrete and final segregation and found that segregation significantly increased at higher W/C ratios. Experimental findings of Khayat end Guizani [2] showed that regardless of water-to-cementitious material ratio, slump, casting height, and mode of consolidation, the incorporation of a viscosity-modifying admixture significantly enhanced the resistance to bleeding, settlement, and segregation. Bois et al. [4], investigating segregation from another point of view, have put forwarded that when concerned with aggregate segregation in a structure; in vertical position, coarse aggregate is an important parameter of segregation and for different coarse aggregate-to-cement ratios (Ca/C), aggregate density significantly affects aggregate segregation in fresh concrete. Neville [5] has pointed out that measuring segregation quantitatively is difficult though some tests, prior to the placement of concrete, are an indication of the potential of segregation. According to him, several factors influence the segregation of concrete, such as the grading of the mix, the method of handling of the concrete, and the manner by which the concrete is placed.
The aim of the concrete industry is to obtain a final product with minimal segregation and high strength. To obtain a desired product, fresh concrete is needed to be workable. The workability of fresh concrete depends on a number of parameters such as water content, mixture elements of the concrete, particle size and shape of aggregates etc. Thus, the workability of the fresh concrete is strongly related to its rheological properties. Ferraris [6] defined workability both qualitatively as the ease of placement and quantitatively by rheological parameters. Iwasaki [7] listed some of the major definitions of workability given by professional societies. Tattersall’s [8] interpretation of workability is “the ability of concrete to flow in mould or formwork perhaps through congested reinforcement; the ability to be compacted to a minimum volume, perhaps the ability to perform satisfactorily in some transporting operations or placing processes and may be other requirements as well”. Ritchie [9] emphasized on three features on the whole, in which one of them is stability. The stability is linked to bleeding and segregation. As a result, the segregation that has a reasonable importance in placing fresh concrete can be related and measured with physical factors.
According to Ferraris [6], concrete is really a concentrated suspension of solid particles (aggre-gates) in a viscous liquid (cement paste). It is obvious from the equations used in the literature that, at least two parameters are needed to define the flow of the fresh concrete. In the case of a concentrated suspension such as concrete, it has been shown by Tattersall [8], and Struble and Uang [10] that a yield stress exists. According to Tattersall [8], the most common rheological parameters of the fresh concrete used to qualify workability, are the yield stress and plastic viscosity as defined by the Bingham equation. de Larrard et al. [11], found that in some cases, the Herschel-Bulkley equation suited better to describe the concrete flow. Herschel-Bulkley equation contains three parameters, one of which does not represent a physical entity. It has been shown by de Larrard et al. [11] that in certain concretes, such as self-consolidating concretes, this is the equation that best describes their behaviors. However, the Bingham equation is commonly employed in practice. As shown by Tattersal [8], the flow of real concrete seems to follow this equation fairly well in most cases. Recently, further researches have been conducted both analytically and experimentally by Bilgil et al. [12], Safawi et al. [13], Ng et al. [14], Li, [15], Leeman and Winnefeld [16], Bentz [17], Roussel et al. [18], Patzák and Bittnar [19], Bethmont et al. [20], Chidiac and Mahmoodzadeh [21].
In this paper, placing of fresh concrete and final aggregate segregation were numerically investi-gated. The scenario was that normal performance concretes with different W/C ratios was filled from bottom of formwork at different inlet velocities. A group of particles were introduced at the formwork inlet and segregation was studied through the trajectories of these particles. The particles were allowed to change momentum with continuous phase. The rheological properties of the fresh concrete were obtained from Ferraris and de Larrard [22]. Range of operation parameters taken into consideration are inlet velocity, initial solid fraction and formwork geometry.
2. Problem Considered
The schematic sketch of the test problem, which consists of the formwork-filling systems, is shown Figure 1. A cylindrical formwork geometry which had a uniform cross-section was considered. Wall shear stress and velocity distribution were kept homogenous by formwork section being chosen as circle. Because rectangular or square sections cause difficulties and constraints in calculations since secondary flows, different wall shear stresses, and different velocity distributions occur especially in the corners of the formworks. The fresh concrete in plastic form enters from the bottom of the formwork and progressively rises in the formwork placing a free surface. The radius of the formwork were chosen to be 0.30 m. Fresh concrete which, has a density of 2400 kg/m3, was employed as the plastic form.
3. Formulation
A mathematical representation of the formwork filling process requires solution of the equations governing the conservation of mass, momentum along with constitutive equation representing the slurry behavior and particle dynamics. A group of particles was introduced at the inlet of formwork and the particles were allowed to change momentum with a continuous phase.
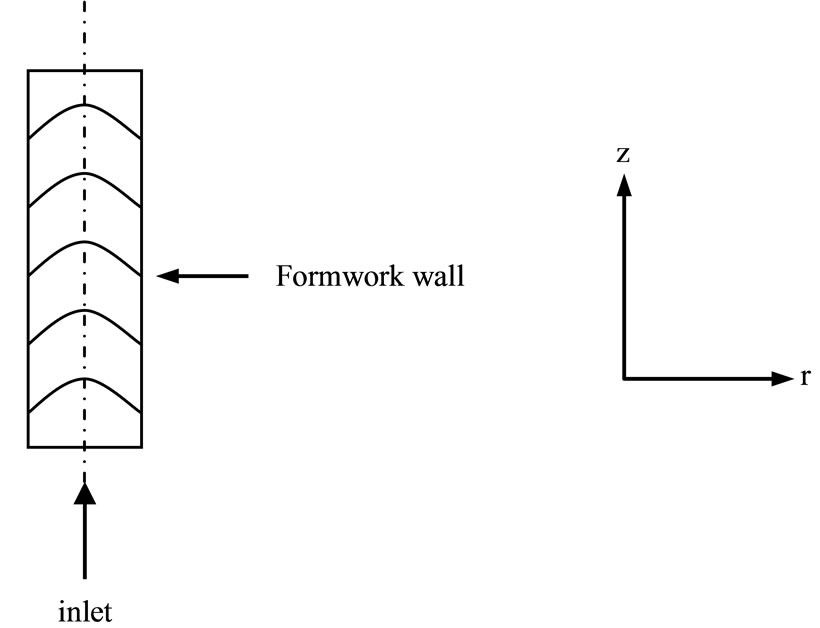
Figure 1. Schematic sketch of test problem considered (cylindrical formwork).
The governing equations for a filling formwork with concrete of plastic form can be expressed in cylindrical co-ordinates as:
Continuity equation
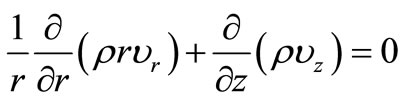 (1)
(1)
Axial momentum
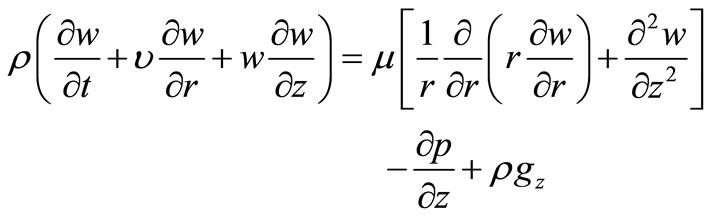 (2)
(2)
Radial momentum
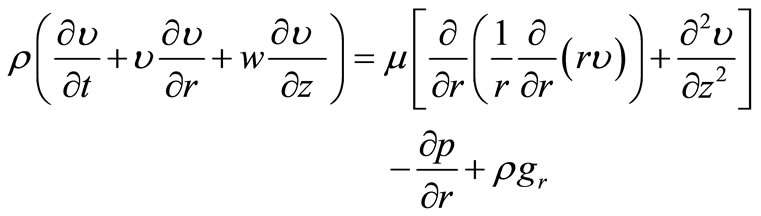 (3)
(3)
where v and w are the radial and axial velocities respectively, p is the static pressure. de Lerrard et al. [11] suggested to employ Herchel-Bulkley equation in order to represent the rheological properties of the fresh concrete due to its non-Newtonian behavior. This relates shear stress to shear strain rate based on a power function;
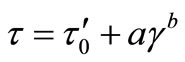 (4)
(4)
where, t is the shear stress, g is the shear strain rate imposed on the sample, 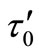 is the yield stress, a and b are new characteristic parameters describing the rheological behavior of concrete. In this case plastic viscosity can not be calculated directly. By Ferraris et al. [23], the yield stress was calculated by means of the HerchelBulkley equation, while the viscosity was calculated using the following equation;
is the yield stress, a and b are new characteristic parameters describing the rheological behavior of concrete. In this case plastic viscosity can not be calculated directly. By Ferraris et al. [23], the yield stress was calculated by means of the HerchelBulkley equation, while the viscosity was calculated using the following equation;
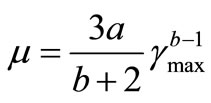 (5)
(5)
where, m is the slope of the straight dotted line, gmax is the maximum shear strain rate achieved in the test, a and b are the parameters as calculated by the Herchel-Bulkley equation. In calculating the viscosity of the fresh concrete, the values in Table 1 were used.
3.1. Particle Physics
The evolution of the particle position Zp was determined from the solution of the following equation proposed by Mat et al. [24];
 (6)
(6)
in which wp is the particle velocity vector, obtained from
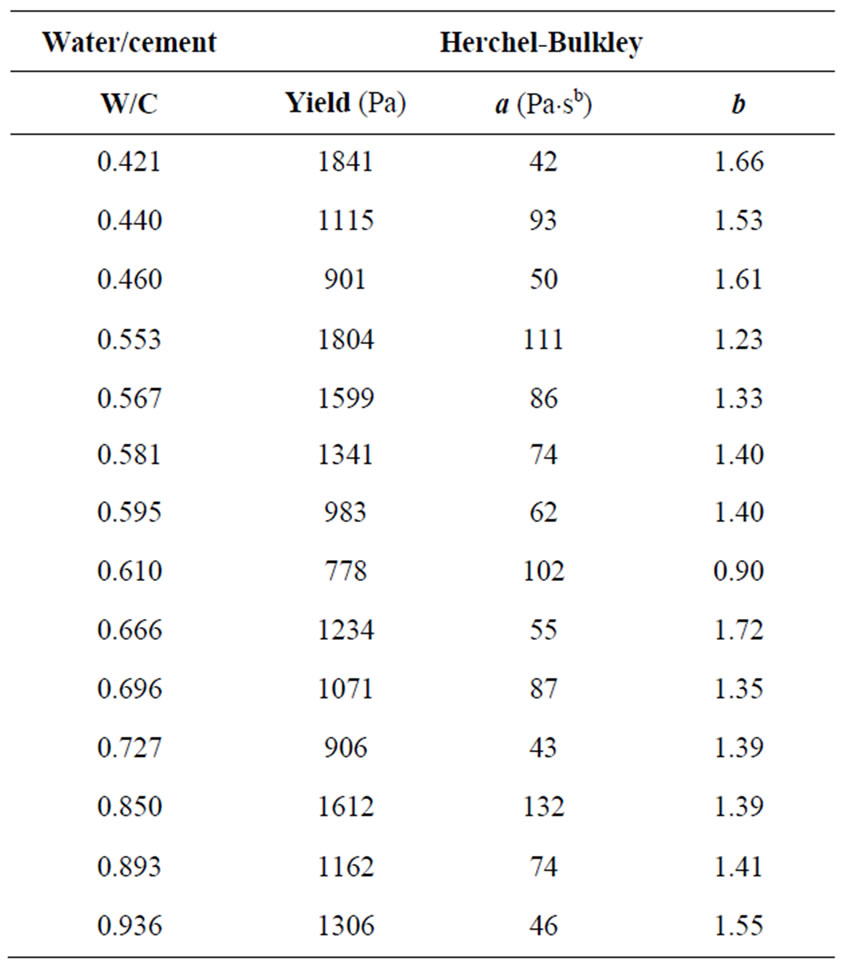
Table 1. The values used in calculating the viscosity of fresh concrete (Ferraris and de Larrard, 1998).
the following particle momentum equation:
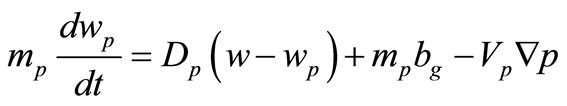 (7)
(7)
where mp is the mass of particle, Dp is the drag function, Vp is the volume of particle, p is the pressure, w is the continuous phase velocity and bf is the buoyancy factor.
Drag function Dp can be expressed as (Fueyo et al., [25]);
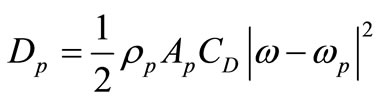 (8)
(8)
where Ap is the particle projected area and CD is the drag coefficient. CD was calculated from a correlation by developed Clift et al. [26]:
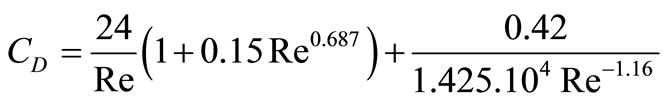 (9)
(9)
where Re is a particle Reynolds number defined as;
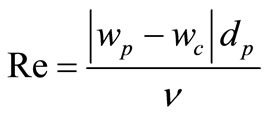 (10)
(10)
where; ν is the kinematics viscosity of the continuous phase and dp is the particle diameter.
The buoyancy factor is given as:
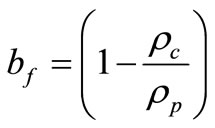 (11)
(11)
3.2. Initial and Boundary Conditions
The formwork was initially assumed to be filled with a quiescent gas (air). The semi-solid slurry was allowed to fill the formwork at t > 0. Only half of the formwork was taken into considered due to the symmetry on the formwork axis. The formwork wall was assumed to be impermeable and a non-slip condition to be valid on the wall. The initial and boundary conditions can be expressed mathematically as
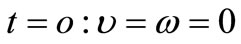 (12)
(12)
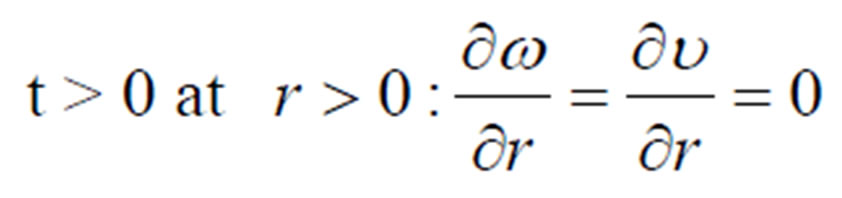 (13)
(13)
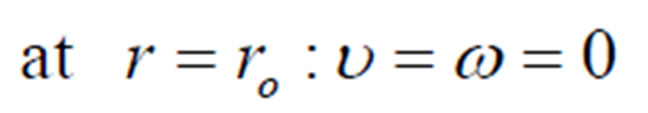 (14)
(14)
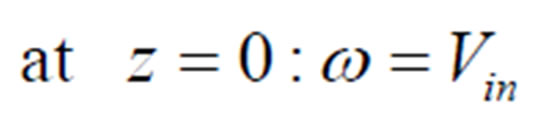 (15)
(15)
4. Numerical Method
The governing equations were solved numerically with a fully implicit, finite domain scheme embodied in the PHOENICS (Rosten and Spalding, [27]) code. PHOENICS is a general purpose CFD software that discritize the Naiver-Stockes equation using a control volume methodology. The code employs a staggered grid arrangement in which velocities are located at the forces of tecontrol volume. The velocity pressure coupling is handled by a simple type algorithma [28]. Since the mold filling operation involves a free surface or the interaction of two distinct media (slurry and air) separated by sharply deformed interfaces, the discretization of the governing equation with a conventional upwind scheme usually results in a false numerical diffusion, thus a van Leer scheme (Van Leer, [29]) was employed to resolve such property interface.
Due to the coupling between the transport equations governing the continuous phase and particles, a threestep solution procedure was employed. In the first step, the continuous-phase equations were solved assuming that there was no particle. The next step followed the integration of particle equations using the current value of continuous phase velocity and calculation of the inter-phase sources. The continuous phase equations were solved again including the particles in the last step. This procedure was repeated until a converged solution was obtained.
A hx30 grid system was employed in all computations. This grid system and a uniform time step of 0.001 s were found to be sufficiently refined for a numerically accurate result. A typical calculation requires approximately 2 hours of CPU time on a personal computer.
5. Result
Several factors could be investigated in a given fresh concrete problem; however only the factors such as formwork geometry, inlet velocity and solid fractions were considered in this study. Seventy-five percent of the inlet area was employed as the nozzle by which the concrete in plastic form entered the formwork in all cases. The cases considered in this study were summarized in Table 2.
The aggregate segregation varies depending on the formwork filling velocity. In this study, the optimum filling velocity of the fresh concrete to the mould was taken as Vin = 0.8 m/s. As can be seen from Bilgil and Yeşilyurt [30] the lower the percentage of segregation the higher the inlet mould velocity is. It can be seen that after Vin = 0.8 m/s inlet formwork velocity the percentage of segregation falls dramatically. On the other hand, the inlet velocity of Vin = 0.8 m/s is appropriate for concrete discharge pump in practice.
Figure 2 shows the evolution of the slurry interface and velocity profiles for the cylindrical formwork at time spans of t = 0.1, 0.5 and 0.9 sec. for all Vin only half of the formwork was illustrated due to the symmetry. It is seen that slurry interface exhibits a jetting characteristics which ingresses as filling progresses. The velocity profile is higher on the axis while lower at the formwork walls.
Trajectories of the representative velocity of aggregate particles in flow concrete were shown in Figure 3. Each line in Figure 3 shows the orbit of one aggregate particle. In Figure 3, the behaviors of the aggregate granules during infilling into the mould with regard to different W/C ratios were given as samples. It is seen that a portion of particles continuously attaches to the wall as the filling progresses. With the concentration of concrete, segregation starts before the mould is filled totally. That phenomenon is partially expected in the practice as well. But in the theoretical study, aggregate segregation was observed to be higher in the low W/C ratios.
In Figure 4, the variation of aggregate segregation compared to the mould height was studied. h represents the height of the mould in this and subsequent figures. The fractionation was quantified from the following relation:
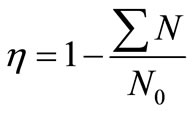 (16)
(16)
where N0 is the total number of particles introduced at the inlet and 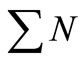 is the predicted sum of the all particles that reached the top of the mould. On the top end of the formwork, the aggregate segregation is at its maximum value. This is the result of tapered mould walls that
is the predicted sum of the all particles that reached the top of the mould. On the top end of the formwork, the aggregate segregation is at its maximum value. This is the result of tapered mould walls that

Table 2. Cases considered (Ferraris and de Larrard, 1998).
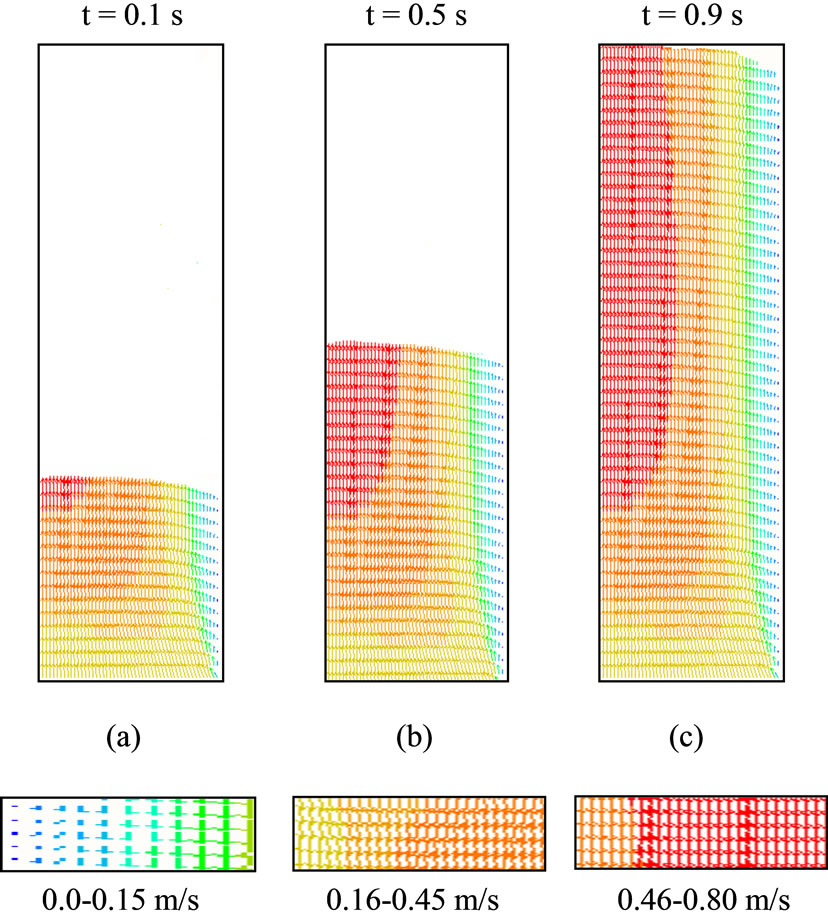
Figure 2. Advance of the slurry interface and corresponding velocity profiles for cylindrical formwork (for W/C = 0.567).
prevent motion of the particles, and recirculation zones that develop near the walls. That result, is the one expected in practice. In Figure 4, only values of maximum and minimum W/C ratios and the ratios at which minimum segregation occurs were given since the table would

Figure 3. Aggregate particle trajectories for cylindrical formwork.
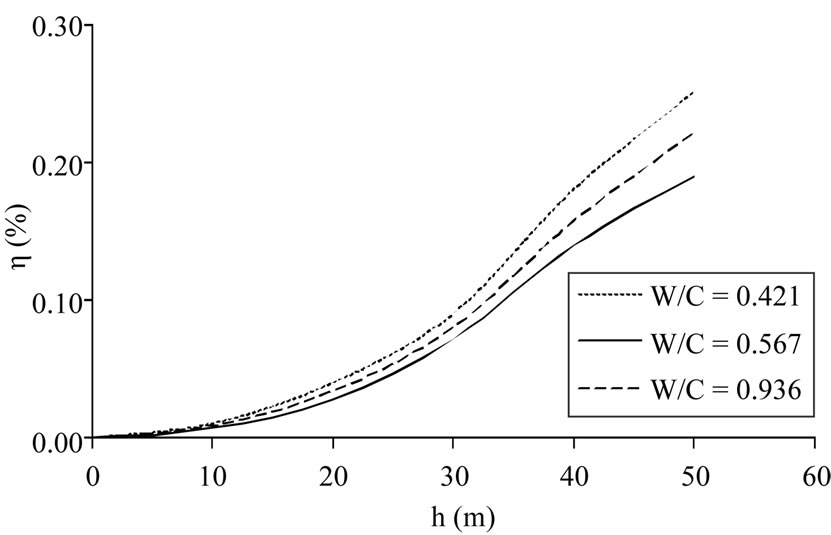
Figure 4. Effects of Water/Cement (W/C) ratios on aggregate segrega-tion.
be too complicated all W/C ratios were shown in case. As seen in Figure 4, aggregate segregation proved to have been parallel along with the height of the formwork. It may be thought that the distribution of particles of the aggregate is denser, as the water will not be uniform in a mixture where the quantity of water more. But in such a mixture segregation came into being lesser than expected. That case can be said to have sourced from the viscosity of the mixture.
In Figure 5, the variation of aggregate segregation of the fresh concrete were presented compared to the different W/C ratios. But in low W/C ratio, segregation started to fall down and at the value of W/C 0.567 minimum segregation is obtained. On higher W/C ratios, segregation started to rise again. Again, on the level of W/C of 0.666, 0.696 and 0.727 aggregate segregation were observed to be at higher levels. It can be told that this case sources from the lack of homogenous distribution of the granules in fresh concrete mixtures, or from the possible experimental mistakes in determining viscosity values. As a result, the case where the segregation is at its minimum in placing the fresh concrete is the one in the mixture where W/C ratio is 0.567.
In Bilgil’s and Yeşilyurt’s [31] studies, fresh concrete having the plastic consistency is relatively easy to be processed. Additionally the most appropriate possible concrete’s W/C ratio was observed to be between 0.50 and 0.65 and it was seen that with this ratio more resistible concrete could be obtained.
In Figure 6, variable viscosity values were given compared to different W/C ratios. It is a known fact that in the vicinity of the formwork walls, higher shear stress would occur. In the parts where the shear stresses are higher the viscosity values will decrease.
According to Murata and Kikukawa [32], the temperature of the mixture and viscosity of the concrete varies in considerably small values, but are linear when compared to the W/C ratio. But in this study, the temperatures of the mixture and medium were neglected.
In Figure 7, the distribution of inlet velocity of the fresh concrete during its filling into the form work was given. As seen in the figure, the flow characteristic of the fresh concrete has non-Newtonian characteristics additionally, when the inlet velocity was analyzed between 0.25 and 0.80, it was observed that velocity distributions exhibited similar characteristics. Since the velocity distribution depends on the viscosity, and results in Figures 6 and 7 supports each other.
6. Conclusions and Discussion
Flow characteristics of fresh concrete exhibits non-Newtonian behavior. The components that compose fresh
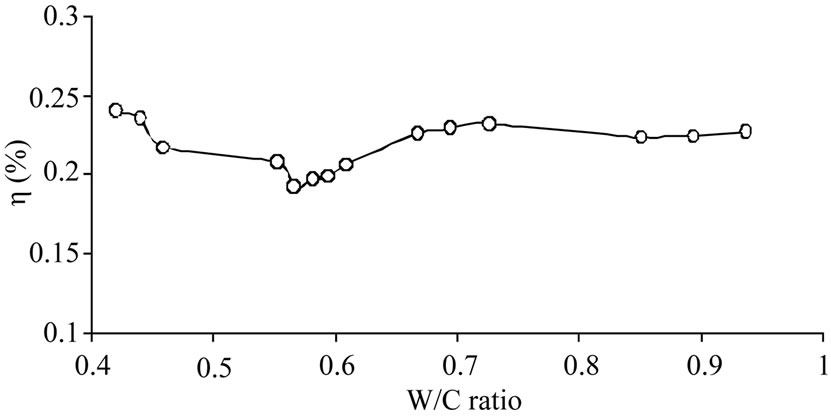
Figure 5. Aggregate segregation in different ratios of W/C.

Figure 6. Viscosity values in different ratios of W/C.
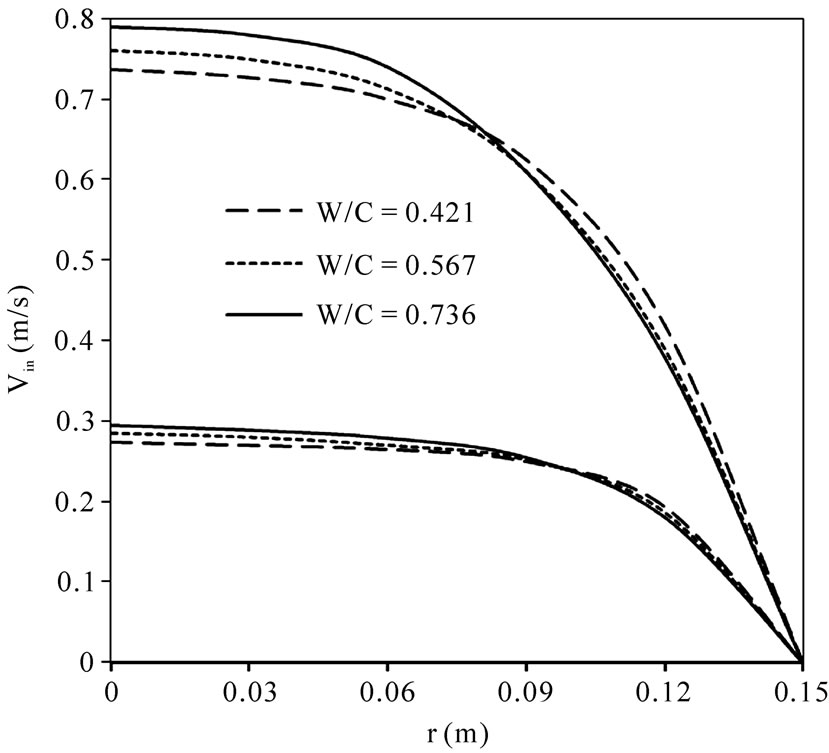
Figure 7. Velocity distribution in different ratios of W/C.
concrete, and rheological characteristics of fresh concrete have significant importance in investigating non-Newtonian behaviors and for workability of concrete. In practice, workability of concrete is controlled by means of slump value. But simply the yield stress can be determined if only the slump value is depended on. However, in today’s advanced concrete technology, besides yield stress, it is frequently proposed that the viscosity should also be taken into consideration in order to obtain high performance concrete. For this reason, all rheological characteristics and mixing parameters of concrete were based on but the segregation of fresh concrete (or workability) was merely investigated from theoretical point of view.
In practice, geometric shape of formworks are commonly rectangular or sequare section. Besides, steel reinforcement exists in formworks when concrete is freely poured from the upper part of the formwork, differing wall shear stresses and steel reinforcement that block the aggregate particles make segregation inevitable. To analyze such a system theoretically is considerably hard since it implicates highly complex relationships. For this reason, formwork geometry was designed to be circular and without reinforcement to minimize uncertainties and to make the system theoretically more analyzable. Meanwhile, though concrete is not injected from bottom of formworks in today’s construction industry, in this study, concrete was supposed to have been filled this way to make the theoretical investigation easy.
The aim of the study is to emphasize the necessity of viscosity for high performance concretes. Because viscosity, namely workability of concrete changes according to varying W/C ratios even if the amounts of components remain the same. It was determined that, for a low W/C ratio of 0.421, and yield stress of 1841 Pa, viscosity would rise and segregation increase; and for a high W/C ratio of 0.936 and yield stress of 1306 Pa, viscosity and segregation would decrease. The minimum aggregate segregation has occurred at the W/C ratio of 0.567 and yield stress of 1599 Pa. In cases where the W/C ratios of the fresh concrete were 0.55 and 0.60, segregation of aggregates was observed to have been lesser.
Yield stress varies dramatically between the ranges of 778-1841 Pa. However, it is difficult to interrelate segregation with this interval and it is assumed to be constant in practice. The most important result achieved by this research is that viscosity should also be considered in evaluating workability of concrete.
In practice, concrete is conveyed to upper elevations by means of pump hoses circular in cross section. With the method proposed in this study, the segregation that may take place in the hose of pump can easily be examined. Furthermore, by applying the studied method in precast production facilities, concretes of high compasity and high performance characteristics can be produced.
7. Acknowledgement
Author would like to thank to Dr. Mahmut MAT of Nigde University for setting up the Problem in PHOENICS and useful advices. They would like to thank also Dr. Ferraris for her valuable comments and her authorization to let us use her data.
8. REFERENCES
- M. Hoshino, “Relationships between Bleeding, Course Aggregate and Specimen Height Concrete,” ACI Materials Journal, Vol. 86 No. 2, 1989, pp. 228-234.
- K. H. Kayahat and Z. Guizani, “Use of Viscosity-Modifying Admixture to Enhance Stability of Fluid Concrete,” ACI Materials Journals, Vol. 94, No. 4, July 1997, pp. 332-340.
- T. Soshiroda, “Segregation Characteristics of Concrete Containing a High-Range Water-Reducing Admixture,” ACI Special Publication, Vol. 68, January 1981, pp. 121- 138.
- K. Bois, A. Benally and R. Zoughi, “Near-Field Microwave Scattering Analysis of Concrete Materials Using Open-Ended Waveguide at sand x-Band,” SPIE Symposium on Nondestructive Evaluation Techniques for Aging Infrastructure Manufacturing, San Antonio, March 1998.
- A. M. Neville, “Properties of Concrete,” 4th Edition, John Wiley & Sons, Hoboken, 1996.
- F. C. Ferraris, “Measurement of Rheological Properties of High Performance Concrete: State of the Art Report,” Journal of Research of the National Institute of Standards and Technology, Vol. 104, No. 5, September-October 1999, pp. 461-478.
- N. Iwasaki., “Estimation of Workability-Why has the Sump Remained Being Used So Long?” Concrete Journal, Vol. 21, No. 10, 1983, pp. 4-12.
- G. H. Tattersall, “The Workability of Concrete,” A Viewpoint Publication, PCA, 1976.
- A. G. B. Ritchie, “The Triaxial Testing of Fresh Concrete,” Magazine of Concrete Research, Vol. 14, 1962, pp. 37-41.
- L. J. Struble and X. J. Uang, “Handbook of Analytical Techniques in Concrete Science and Technology,” Noyes Publications Park Ridge, New Jersey, 2001, pp. 333-367
- F. de Larrard, F. C. Ferraris and T. Sedran, “Fresh Concrete: A Herschel-Bukley Material,” Material and Structures, Vol. 31, No. 7, 1998, pp. 494-498. doi:10.1007/BF02480474
- A. Bilgil, B. Oztürk and H. Bilgil, “A Numerical Approach to Determine Viscosity-Dependent Segregation in Fresh Concrete,” Applied Mathematics and Computation, Vol. 162, No. 1, 2005, pp. 225-241. doi:10.1016/j.amc.2003.12.086
- M. I. Safawi, I. Iwaki and T. Miura, “The Segregation Tendency in the Vibration of High Fluidity Concrete,” Cement and Concrete Research, Vol. 34, No. 2, February 2004, pp. 219-226. doi:10.1016/S0008-8846(03)00249-7
- I. Y. T. Ng, H. H. C. Wong and A. K. H. Kwan, “Passing Ability and Segregation Stability of Self-Consolidating Concrete with Different Aggregate Proportions,” Magazine of Concrete Research, Vol. 58, No. 7, 2006, pp. 447- 457. doi:10.1680/macr.2006.58.7.447
- Z. Li, “State of Workability Design Technology for Fresh Concrete in Japan,” Cement and Concrete Research, Vol. 37, No. 9, September 2007, pp. 1308-1320. doi:10.1016/j.cemconres.2007.05.001
- A. Leeman and F. Winnefeld, “The Effect of Viscosity Modifying Agents on Mortar and Concrete,” Cement and Concrete Composites, Vol. 29, No. 5, May 2007, pp. 341- 349. doi:10.1016/j.cemconcomp.2007.01.004
- D. P. Bentz, “Engineering Concrete Performance,” Concrete International, Vol. 29, No. 11, November 2007, pp. 33-37.
- N. Roussel, M. R. Geiker, F. Dufour, L. N. Thrane and P. Szabo, “Computational Modeling of Concrete Flow: General Overview,” Cement and Concrete Research, Vol. 37, 2007, pp. 1298-1307. doi:10.1016/j.cemconres.2007.06.007
- B. Patzák and Z. Bittnar, “Modeling of Fresh Concrete flow,” Computers and Structures, Vol. 87, 2009, pp. 962- 969. doi:10.1016/j.compstruc.2008.04.015
- S. Bethmont, L. D’Aloia Schwartzentruber, C. Stefani, J. L. Tailhan and P. Rossi, “Contribution of Granular Interactions to Self Compacting Concrete Stability: Development of a New Device,” Cement and Concrete Research, Vol. 39, No. 1, January 2009, pp. 30-35. doi:10.1016/j.cemconres.2008.10.007
- S. E. Chidiac and F. Mahmoodzadeh, “Plastic Viscosity of Fresh Concrete – A Critical Review of Predictions Methods,” Cement and Concrete Composites, Vol. 31, No. 8, September 2009, pp. 535-544. doi:10.1016/j.cemconcomp.2009.02.004
- F. C. Ferraris and F. de Larrard, “Testing and Modelling of Fresh Concrete Rheology,” NISTIR 6094, February 1998.
- F.C. Ferraris, F. de Larrard and N. Martys, “Fresh Concrete Rheology: Recent Developments,” Reprinted from Materials Science of Concrete VI, The American Ceramic Society, 735 Ceramic Place, Westerville, 2001, pp. 215-241.
- M. D. Mat, K. Altınışık, F. Karakoç and Y. Kaplan, “Mathematical Modelling of Fractionation during the Mold Filling of Semi-Solid Metal Slurries,” Turkish Journal of Engineering and Environmental Sciences, 1999, pp. 281-288.
- N. A. Fueyo, I. Hamill and Q. Zhang, “The GENTRA User Guide,” CHAM Limited (UK) Technical Report, TR/211, 1992.
- R. Clift, J. R. Grace and M.E. Weber, “Bubbles, Drops and Particles,” Academic Press, New York, 1978.
- H. Rosten and D.B. Spalding, “PHOENICS Beginner’s Guide and User’s Manual,” CHAM Limited (UK) Technical Report, TR/100, 1986.
- “An Introduction to CHAM, Its Software and Services,” 2011. Internet Available: http://www.cham.co.uk
- B. Van Leer, “Towards the Ultimate Conservative Difference Scheme, IV: A New Approach to Numerical Convection,” Journal of Computational Physics, Vol. 23, No. 3, March 1977, pp. 276-299. doi:10.1016/0021-9991(77)90095-X
- A. Bilgil and E. Yeşilyurt, “Mathematical Modelling of Aggregate Segregation during Concrete Flow,” 2nd International Symposium, European University of Lefke, 2002
- A. Bilgil and E. Yeşilyurt, “Concrete Properties and Tests,” Erciyes University Press, Kayseri, 1999.
- J. Murata and H. Kikukawa, “Viscosity Equation for Fresh Concrete,” ACI Materials Journals, Vol. 89, No. 3, May 1992, pp. 230-237.
Nomenclature
A particle projected area,
a, b parameters in the Herchel-Bulkley equation
CD drag coefficient
d particle diameter
D drag function
H formwork height
m mass
N number of particles
p static pressure
Re Reynolds number
r radial coordinate
ro radius of formwork
t time
v radial velocity
Vin inlet velocity
w axial velocity
z axial coordinate
g shear rate
D deformation tensor
h fractionation
m viscosity
r density
t shear stress

