Engineering
Vol. 3 No. 9 (2011) , Article ID: 7325 , 11 pages DOI:10.4236/eng.2011.39106
The Simple Model for Bolted Connections in Fire
1Civil Engineering Department, K.N.Toosi University of Technology, Tehran, Iran
2Department of Civil Engineering, Islamic Azad University, central Tehran branch, Iran
E-mail: amir_saedi_d@yahoo.com
Received December 27, 2010; revised June 7, 2011; accepted June 20, 2011
Keywords: Bolted Connection, Elevated-Temperature, Fire, Spring-Stiffness Model, Rotation-Temperature Curves, Moment-Rotation Curves
ABSTRACT
Recent structural collapses caused by fire have focused attention on research concerning fire safety in building design. Steel connections are an important component of any structural steel building as they provide links between the principal structural members. Considering the importance of this matter this paper describes a spring-stiffness model developed to predict the behavior of bolted angle connections bare-steel joints at elevated temperature. The joint components are considered as springs with predefined mechanical properties i.e. stiffness and strength. The elevated temperature joint’s response can be predicted by assembling the stiffness of the components which are assumed to degrade with increasing temperature based on the recommendations presented in the design parameters code. Comparison of the results from the model with existing experimental data showed good agreement. The proposed model can be easily modified to describe the elevated temperature behavior of other types of joint as well as joints under large rotat-ions.
1. Introduction
The properties of steel structures such as load-carrying capacity degrade rapidly in fire due to the reduction in both stiffness and strength of the material. Steel-framed buildings may be subjected to a fire and therefore must be constructed to ensure life safety and property protection. In the past 20 years, there has been much interest in understanding the behavior of different structural elements in fire and experiments have been conducted on steel members and joints either in isolation or as part of a sub-frame assembly or even a full-scale structure. All structural members exposed to fire heat up, but the rate of temperature rise in each member is different. Joints in a steel-framed building tend to heat up slower than the material within the span of the beam because of the presence of additional materials (bolts, plates, angles, etc.) and due to their shielded location i.e. usually beneath a composite floor. In conventional analysis and design of steel and composite frames, beam-to-column connections are assumed to behave either as ‘pinned’ or as fully ‘rigid’ joints [1,2]. Although the pinned or rigid assumption significantly simplifies analysis and design procedures, in practice, the actual joint behavior exhibits characteristics from a wide spectrum between these two extremes. The difference between the two simplified joint types is that pin joints have rotational stiffness while rigid joints display flexibility. Designers may choose a more accurate representation of joint behavior for analysis and design, but many adopt simplified economical methods. Although these simplified approaches are sufficient for designs at ambient temperatures, when steel-framed structures are subjected to fire the behavior of the joints within a frame exerts an even greater influence on overall response. If the behavior of these connections is not considered properly, the analysis may misrepresent the performance of a structure. In general, experimental tests provide reliable results that can describe the behavior of the beam-to-column connections. However, in many cases experiments are either not feasible or too expensive to conduct. Although of high importance, they are always limited in terms of the number of geometrical and mechanical parameters studied, which obviously would not provide comprehensive understanding of connection performance. Therefore Various forms of analysis and modeling methods have been suggested including simple curve-fitting techniques, simplified analytical methods and sophisticated finite element models for both bare-steel and composite joints. The European code for the design of steel structures (EC3: Part 1.8) [3] has adopted a simplified analytical procedure for the design of joints at ambient temperature. This method is based on dividing the joint into its basic components of known mechanical properties. By assembling the contributions of individual components which represent the joint as a set of rigid and deformable elements, the entire behavior of the joint may be determined. This method is known as the spring-stiffness or component method. However, there is a few of elevated temperature component models due to the lack of experimental data that describes the joint’s behavior. This paper describes a spring-stiffness model developed in an attempt to use the component method to predict the behavior of bolted angle bare-steel joints at elevated temperature using the mechanical characteristics of the components that are available in the literature. In the model the joint’s components are treated a springs with predefined characteristics such as stiffness and strength. By assembling the characteristics of individual components, the joint’s response can be predicted with increasing temperatures. Only those parameters representing the stiffness and strength of the joint are degraded with increasing temperatures. Comparison of the results from the model with existing test data generated good results.
2. Spring-Stiffness Modeling
The originality of this ‘Component Method’ is to consider any steel beam-to-column joint as a set of individual components. A beam-to-column joint using the bolted angle connection can be divided into four major zones i.e. flexure, tension, and shear and compression zones. Each zone of the joint can be further divided into a number of components, each of which is simply a nonlinear spring, possessing its own strength and stiffness in flexure, tension, compression or shear, and will be reduced with elevation of temperature.
For each component, the initial stiffness and ultimate capacity is determined and assembled to form a spring model, which is adopted to simulate the rotational behavior of the whole joint. An idealized representation of the bolted angle connections bare-steel joint is shown in Figure 1. Connection components are named in Figure 2.
For simplicity, the flexure zone in the flange of column is represented by a separate spring Kcfb and the flexure zone of the top angle and web angle are represented by springs Kta and Kwa. In addition the tension zone of the column web is represented by spring Kcwt. Simi larly the deformation of the components, ΔT, can be represented by the sum of the deformations of column flange, Δcfb, top angle, Δta, web angle, Δwa, tension in bolts, Δbt, pressure in bolts, Δbp, and tension zone of the
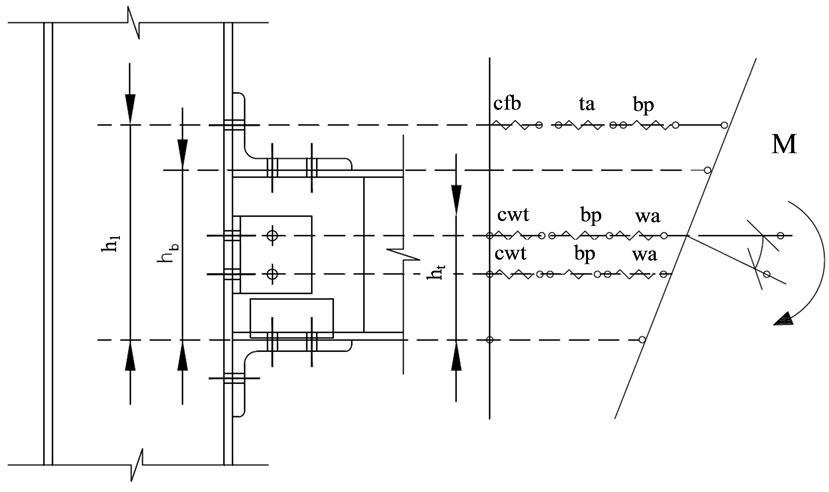
Figure 1. General representation of the proposed model.

Figure 2. Specimen details.
web column, Δcwt, (Equation 1).
At initial elastic stage, small deformation assumption is adopted. The following equations can be obtained:
 (1)
(1)
Considering that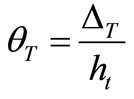 ,
, 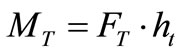 , and The global rotational stiffness of the joint
, and The global rotational stiffness of the joint 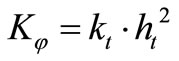 can be determined for any moment at any given temperature based on the assembled stiffness of all components as:
can be determined for any moment at any given temperature based on the assembled stiffness of all components as:
 (2)
(2)
 (3)
(3)
where:
 (4)
(4)
With the spring model, the ultimate moment of the joint can be estimated using the following expression:
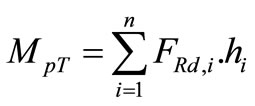 (5)
(5)
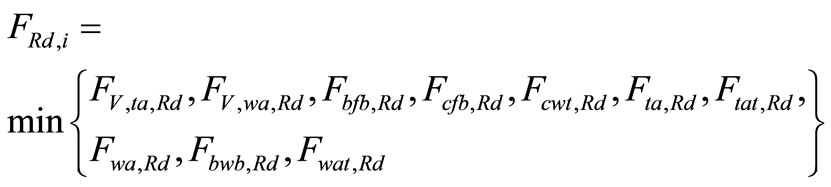 (6)
(6)
After obtaining the stiffness and ultimate load of each component, the moment–rotation relation may be obtained from the following Equation [4]:
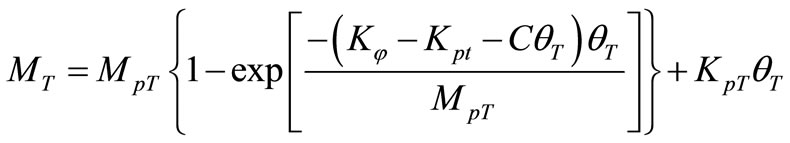 (7)
(7)
where, 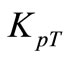 can be expressed as
can be expressed as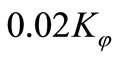 , and a zero value has been recommended for C [4] .Components forces are shown in Figure 3.
, and a zero value has been recommended for C [4] .Components forces are shown in Figure 3.
3. Degradation of the Joint’s Characteristics at Elevated Temperature
When a steel bolted angle connection is subjected to fire, the temperature of the joint will be increased to a high level. At elevated temperature, the elastic modulus and strength of steel will be reduced. The reduction of stiffness and strength of the components was based on the reduction of structural steel at elevated according to EC3: Part 1.2 as shown in Table 1.

Figure 3. Forces in connection components.

Table 1. Properties of structural steel at elevated temperature ( : steel temperature,
: steel temperature, : yield stress,
: yield stress,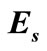 : Young’s modulus).
: Young’s modulus).
However, the reduction of bolt stiffness and capacity is based on recommendations presented by Kirby [5] using Equation (8) to Equation (10).
If
θb ≤ 300˚C then SFR = 1.0 (8)
If
θb < 300˚C ≤ 680˚C then
SFR = 1.0 − (θb − 300) × 2.128 × 10−3 (9)
If
θb < 680˚C ≤ 1000˚C then
SFR = 0.17 − (θb − 680) × 5.13 × 10−4 (10)
where θb is temperature of the bolt and SFR is strength retention factor of the bolt. These reduction factors are suggested by Saedi Daryan et al. via experimental test. [6]
4. Initial Stiffness of Components at Elevated Temperature
In this part, the stiffness of each connection components that is necessary for calculation of Equation (4) is presented [7-10].
4.1. Calculates the Stiffness of Column Flange and Column Web
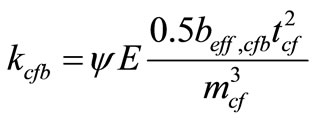 (11)
(11)
where:
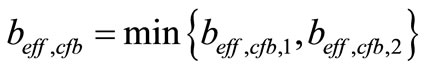 (12)
(12)
 (13)
(13)
c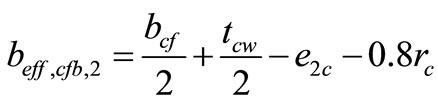 (14)
(14)
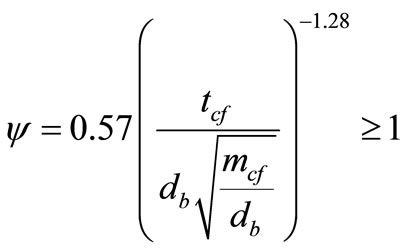 (15)
(15)
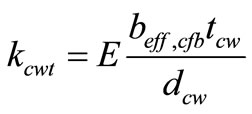 (16)
(16)
4.2. Calculates the Stiffness of Top Angle
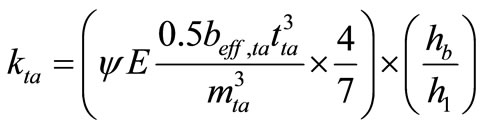 (17)
(17)
where:
 (18)
(18)
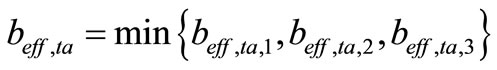 (19)
(19)
 (20)
(20)
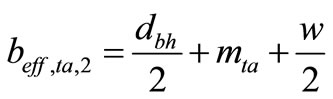 (21)
(21)
 (22)
(22)
 (23)
(23)
4.3. Calculates the Stiffness of Bolt Row
 (24)
(24)
4.4. Calculates the Web Angle Stiffness
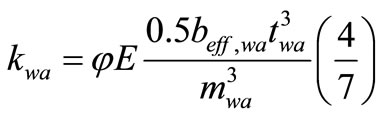 (25)
(25)
where:
 (26)
(26)
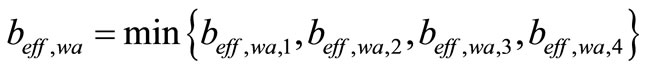 (27)
(27)
 (28)
(28)
 (29)
(29)
 (30)
(30)
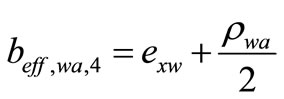 (31)
(31)
5. The Load Capacities of Connection Components
In this part, the Load-caring capacity of each connection components that is necessary for calculation of equation 6 is presented. [11-13]
5.1. Calculate the Shear Force of Bolts in Top Angle and Bolt Force in Beam Flange
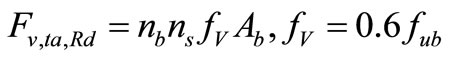 (32)
(32)
 (33)
(33)
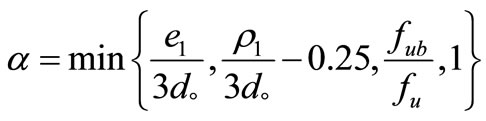 (34)
(34)
5.2. Calculate the Bolt Force in Column Flange
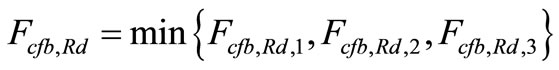 (35)
(35)
 (36)
(36)
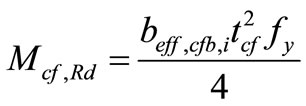 (37)
(37)
 (38)
(38)
 (39)
(39)
 (40)
(40)
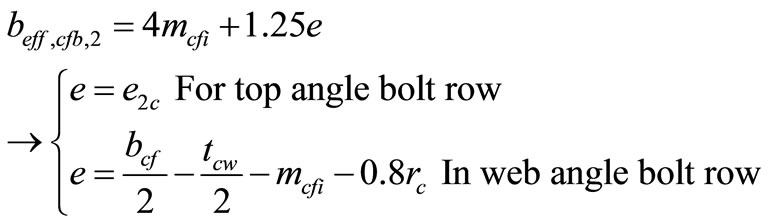 (41)
(41)
 (42)
(42)
 (43)
(43)
 (44)
(44)
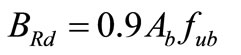 (45)
(45)
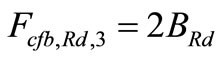 (46)
(46)
5.3. Calculate the Tensile Force in Column Web
 (47)
(47)
 (48)
(48)
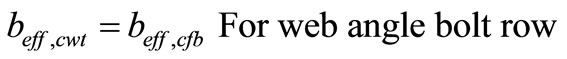 (49)
(49)
5.4. Calculate the Force of Top Angle
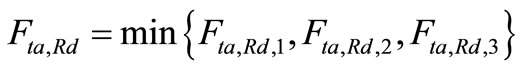 (50)
(50)
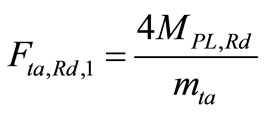 (51)
(51)
 (52)
(52)
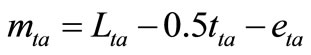 (53)
(53)
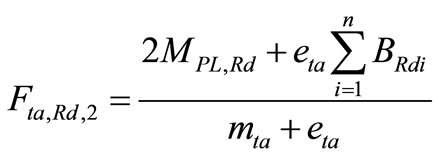 (54)
(54)
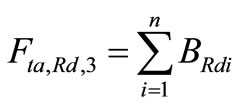 (55)
(55)
 (56)
(56)
5.5. Calculate the Tensile Force in Top Angle and Web Angle Force
 (57)
(57)
 (58)
(58)
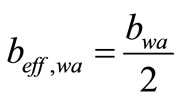 (59)
(59)
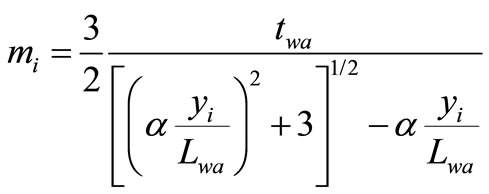 (60)
(60)
 (61)
(61)
 (62)
(62)
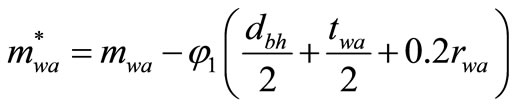 (63)
(63)
 (64)
(64)
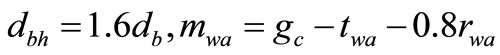 (65)
(65)
5.6. Calculate the Shear Force of Bolts in Web Angle and Beam Web Bending Force and Tensile Force in Web Angle
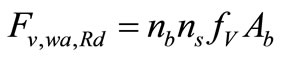 (66)
(66)
 (67)
(67)
 (68)
(68)
 (69)
(69)
6. Accuracy Calibration of the Proposed Model
In order to confirm and evaluate the accuracy of the spring-stiffness model under the fire conditions, four samples of the angle connection with bolts are used by experimental report, presented by Saedi Daryan et al. [6-14]
6.1. Details of Specimens Tested by Saedi Daryan et al.
The specimens were configured in a symmetrical cruciform arrangement that consists of a single 80 cm high column of IPE300 section connected to two 250 cm long cantilever beams of IPE 220 section. The load was applied on a point 2 meters from the end of the beam. All of the bolts in the specimens were tightened to 150 N.m by a torque wrench to ensure consistency. The experimental tests were conducted on two different connection details:
Connection group 1: (SPECIMEN WITHOUT WEB ANGLE) (SOW)
Connection group 2: (SPECIMEN WITH WEB ANGLE) (SWW)
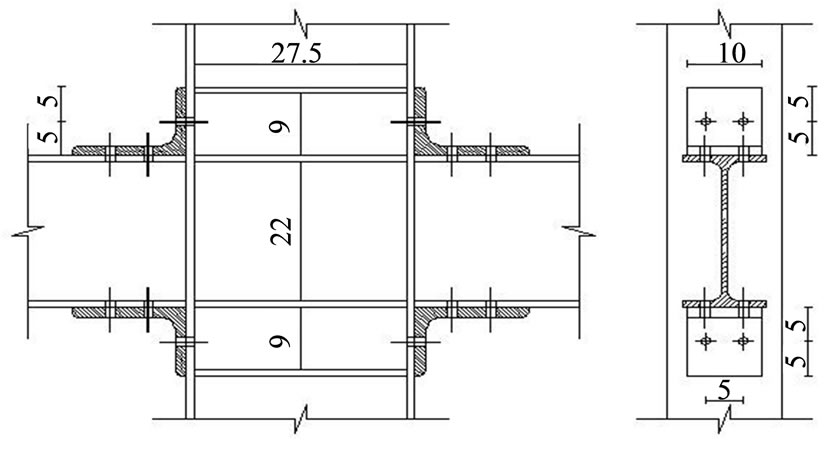
Connection group 1 (SOW) consisted of two angles, one connected to the top flange of the beam and the other connected to the bottom flange. The total system was bolted to the flange of the column. Each angle was bolted to the flange of the beam by six M16 bolts and to the flange of column by two M16 bolts. A detail of this group of connections is shown in Figure 4(a).
The connection group 2 (SWW) had two additional angles compared with connection group 1. These angles were bolted to the web of the beam on one side and to the flange of the column on the other side. Web angles were connected to the web of the beam by two M16 bolts and to the flange of the column by two M16 bolts. Details of this group of connections are shown in Figure 4(b). Details of all specimens are provided in Table 2.
6.1.1. Specimen Loading
The values of applied moment to each specimen in the tests are presented in Table 3. As it can be seen, first the rotation capacity of connection is theoretically calculated and then the applied moment is selected as a coefficient of connection rotation capacity and is applied to the specimens during the test.
The steel material properties of the specimens are presented in Table 4.
The effectiveness of the spring-stiffness model for
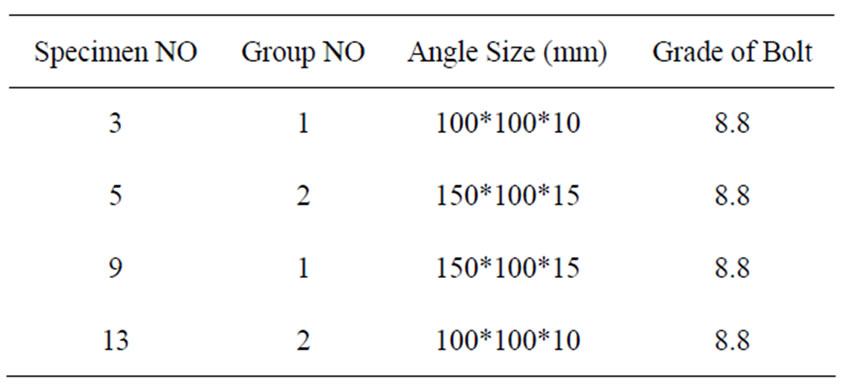
Table 2. Details of specimens tested by Saedi Daryan et al. [6].
 (a)
(a)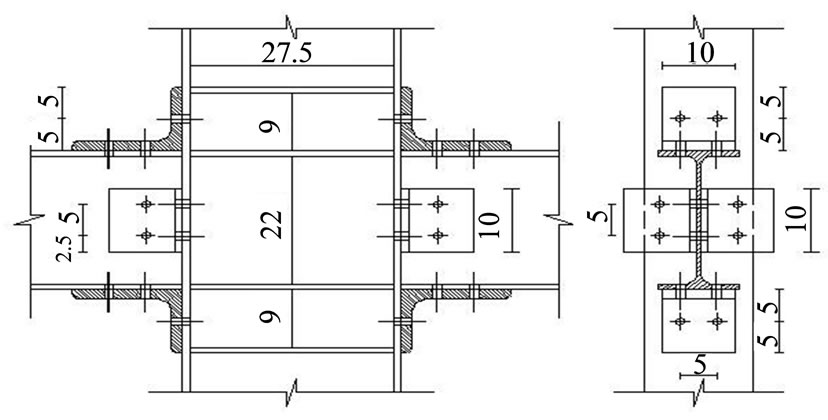 (b)
(b)
Figure 4. Details of the test conducted by Saedi Daryan et al. (a) Connection group 1 (SOW), (b) Connection group 2 (SWW).
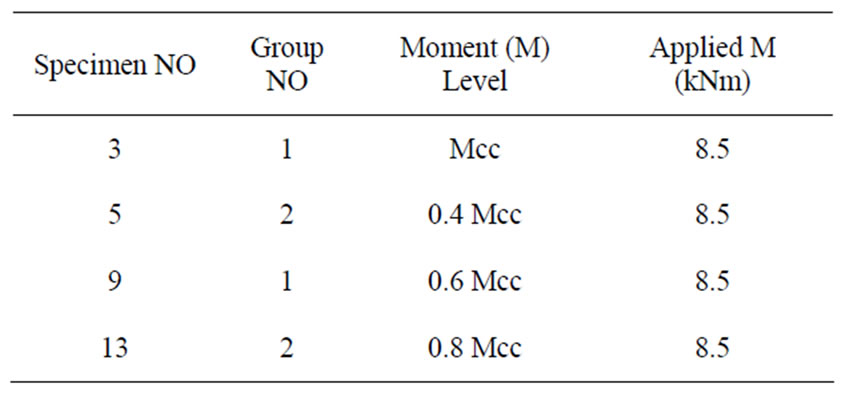
Table 3. The value of applied moment for each specimen in the tests carried out by Saedi Daryan et al.
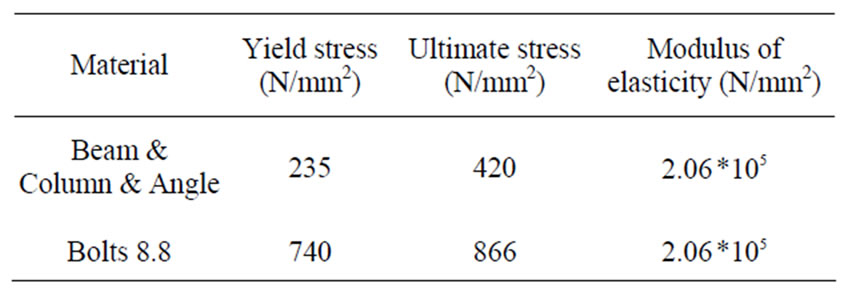
Table 4. Material properties of specimens tested by Saedi Daryan et al.[6].
simulating the behavior of the bolted angle joints subjected to fire may be validated with the experiments. In Figure 5 temperature—rotation carves obtained by experimental tests are compared with the result of spring-stiffness model. In Figure 6, moment—rotation carves presented by Saedi Daryan et al. are compared with the result of spring-stiffness model [15]. It can be seen that the predicted and the measured results of specimens agree with each other quite well. In the case of few specimens, some differences between the results are observed that, these may be due to the different rate of temperature increase. The rate of temperature increase has some influence on the creep strain of steel. So variation of the fire rate may impact on the response of connections. Further study of the influence of creep stain on the behavior of bolted angle joints will be done in the next stage of research. The good agreement of modeling with the test results demonstrates that the spring-stiffness model is a good representation of bolted angle joints. The spring-stiffness model can be used to predict the response of connections as well as of structures with bolted angle joints at elevated temperatures.
7. Conclusions
This research was carried out to simulate the behavior of bolted angle connections in fire with spring-stiffness model. The model is developed according to the specifications of the details and behavior of the connection in elevated temperature. Comparisons of the springstiffness method with experimental results confirm predicted and measured responses both in elastic and plastic zones. This method is capable of predicting the results of the bolted angle connection in elevated temperature with desirable accuracy. However the proposed model requires further development to support following topics which could have an important effect on the connection behavior in high temperature:
• The applicability of the model to predict the joint behavior at higher levels of moment than those presented;
• The model was developed based on isolated joint tests, the effect of axial restrained on the joint behavior needs to be addressed in the model since this can have significant influence on the behavior of the structure in fire as observed from Cardington frame fire tests. Also, the joint behavior during the cooling

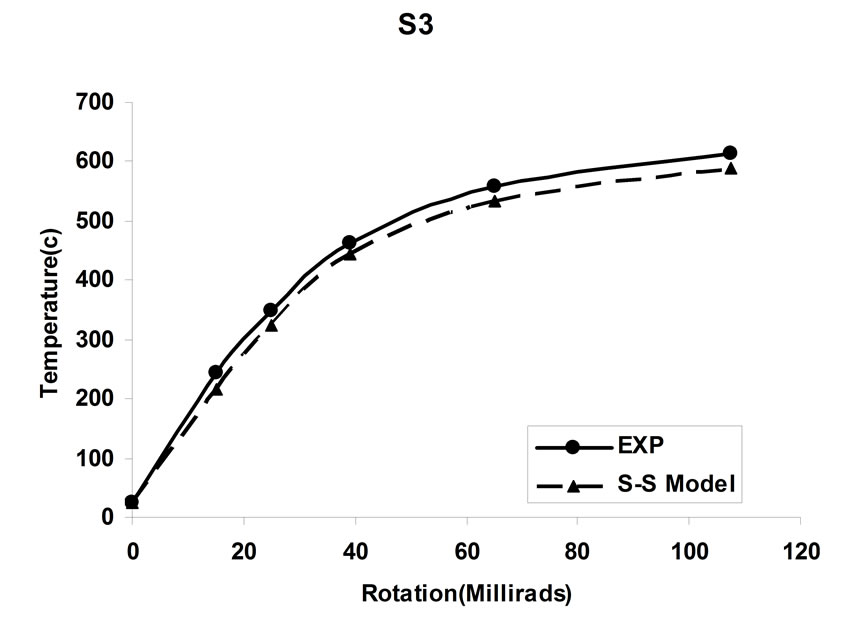

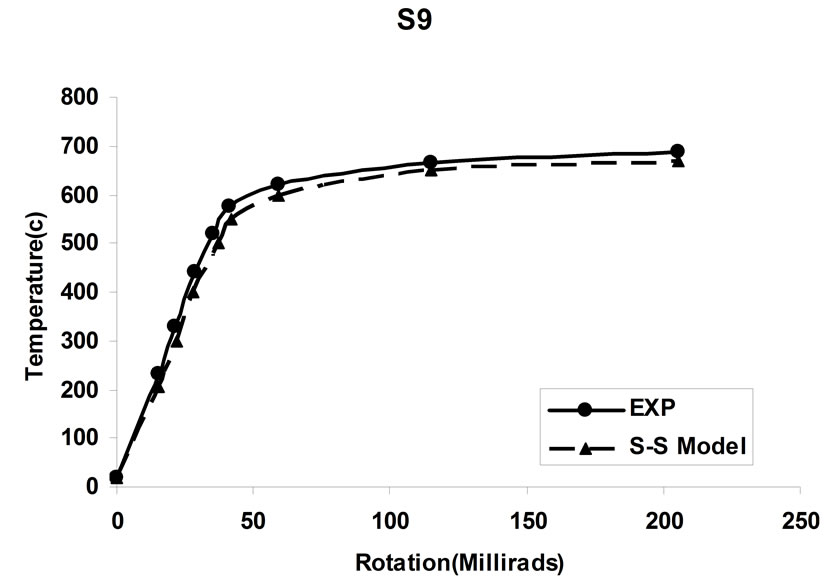
Figure 5. Comparison of temperature—rotation for spring-stiffness model and experimental tests [15].
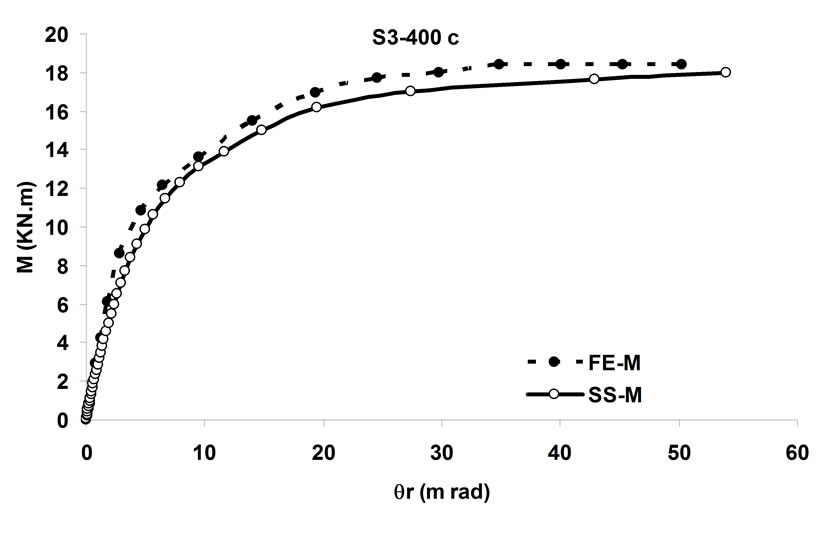
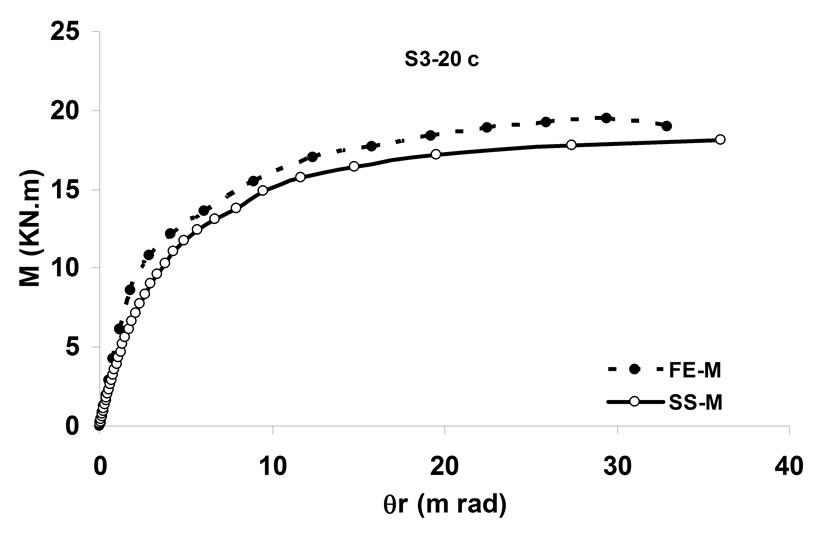
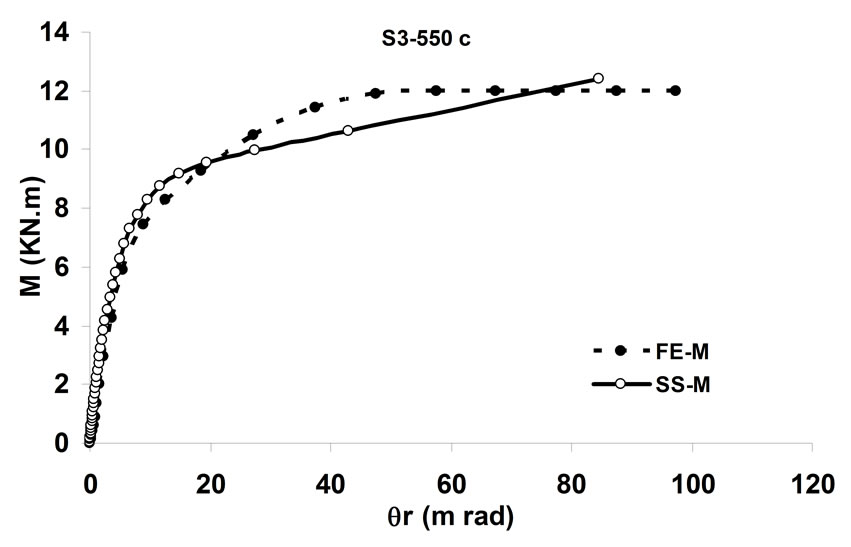
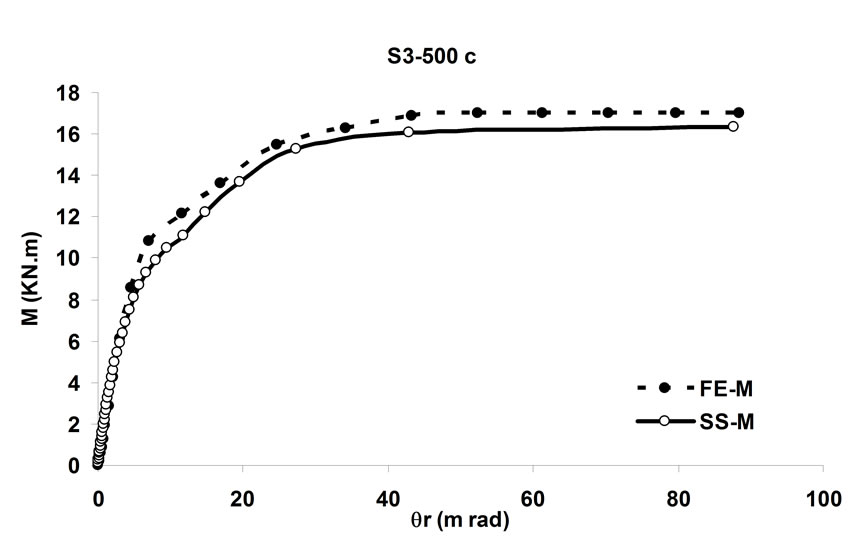

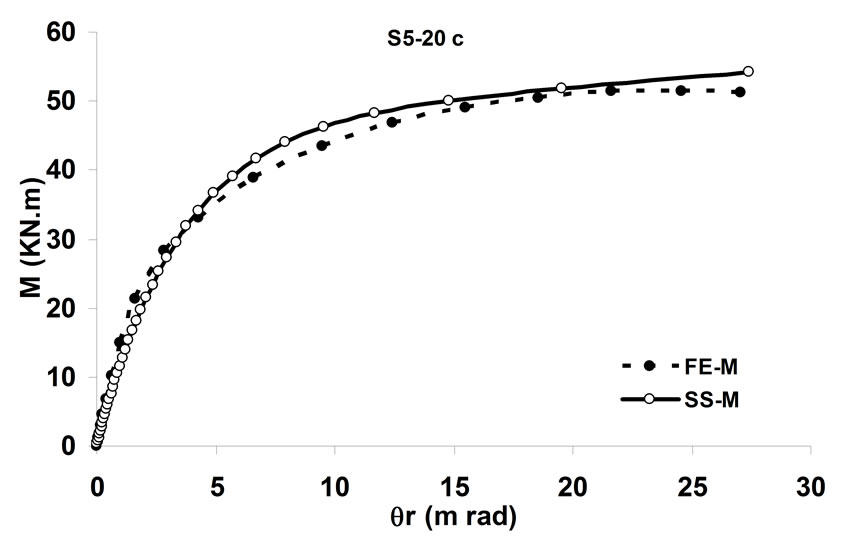

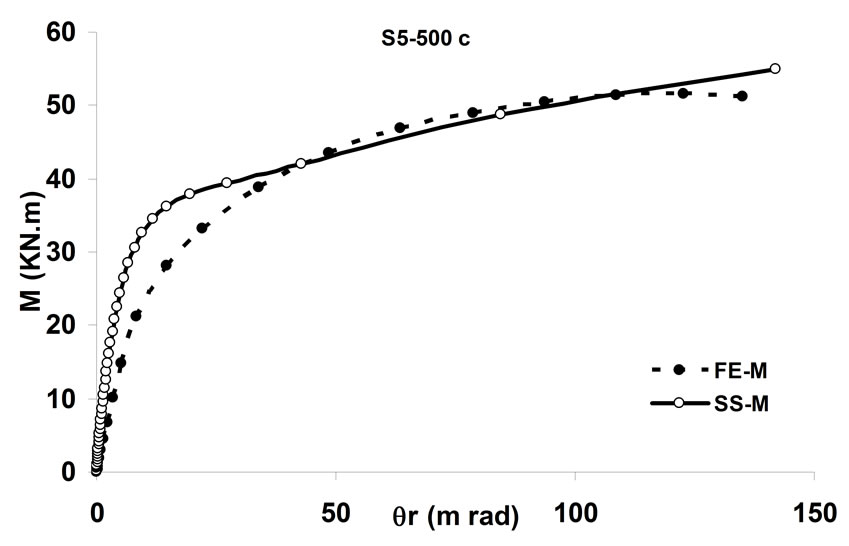
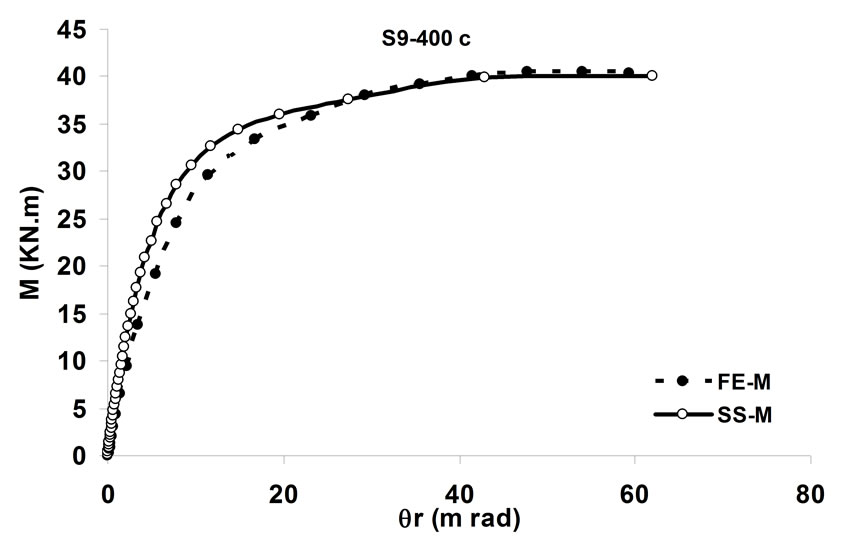
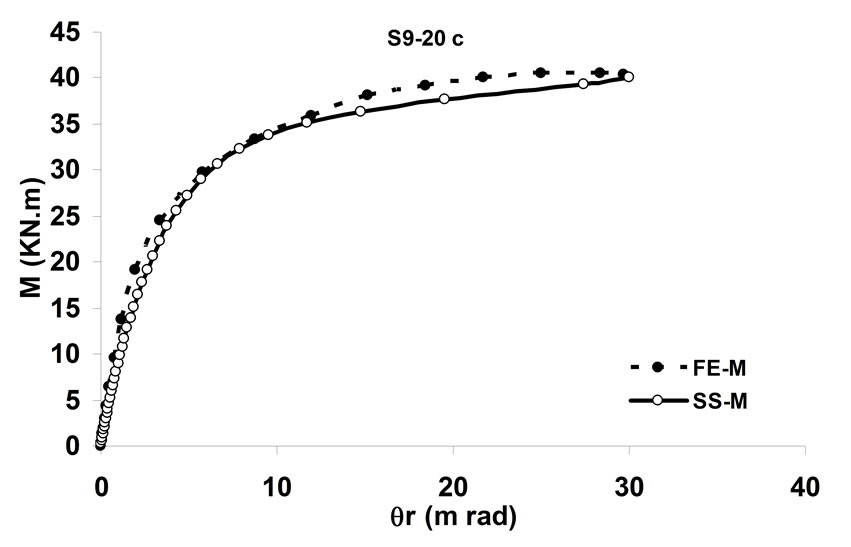

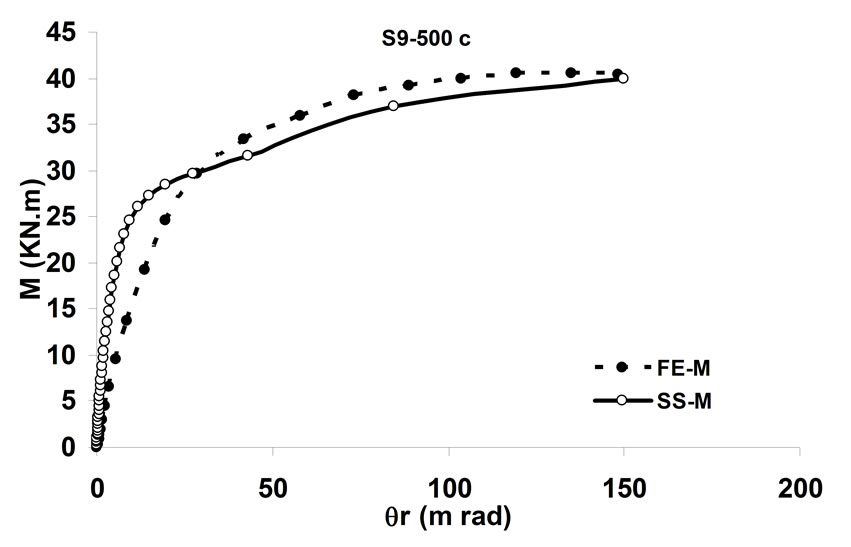
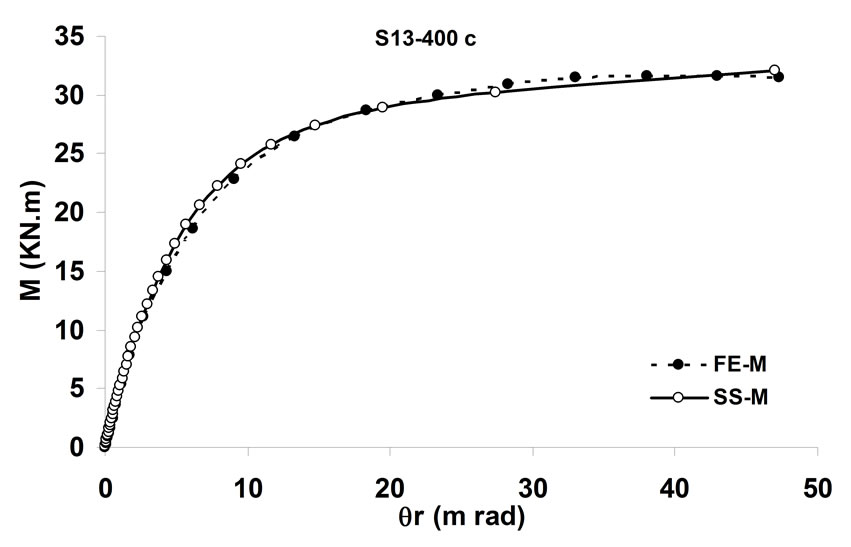
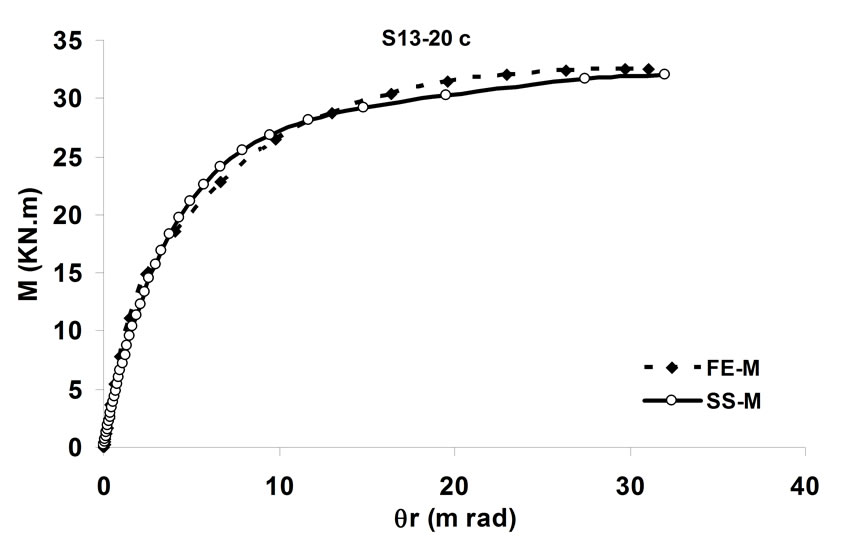

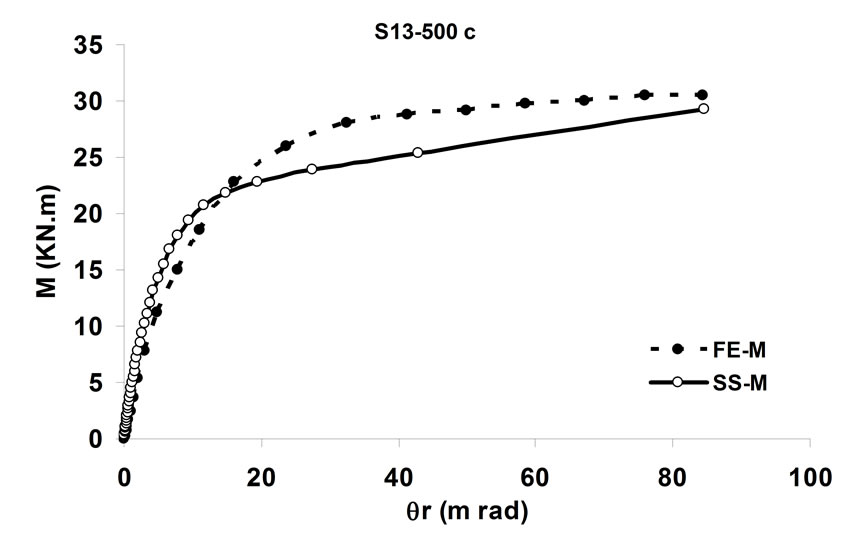
Figure 6. Comparison of moment—rotation for spring-stiffness model and reference [15].
phase needs to be investigated.
8. REFERENCES
- S.W. Jones, P. A. Kirby and D. A. Nethercot, “The Analysis of Frames with Semi Rigid Joints,” Department of Civil and Structural Engineering, University of Sheffield, Sheffield, 1981.
- W.-Y. Wang, G.-Q. Lia and Y.-L. Dong, “Experimental Study and Spring-Component Modelling of Extended End-Plate Joints in Fire,” Journal of Constructional Steel Research, Vol. 63, No. 8, 2007, pp. 1127-1137. doi:10.1016/j.jcsr.2006.10.006
- Euro Code 3, “Design of Steel Structures, Part 1-8: General Rules Design of Joints,” European Committee for Standardization (CEN), 2003.
- K. L. Yee and R. E. Melchers, “Moment–Rotation Curves for Bolted Joints,” American Society of Civil Engineers, Vol. 112, 1986, pp. 615-635.
- B. R. Kirby and R. R. Preston, “High Temperature Properties of Hot Rolled Structural Steels for Use in fire Engineering Design Studies,” Fire Safety Journal, Vol. 13, No. 1, 1988, pp. 27-37. doi:10.1016/0379-7112(88)90030-6
- A. S. Daryan and M. Yahyai, “Behavior of Bolted Top-Seat Angle Connections in Fire,” Journal of Constructional Steel Research, Vol. 65, No. 3, 2009, pp. 531-541. doi:10.1016/j.jcsr.2008.07.021
- A. Azizinamini, J. H. Bradburn and J. Radziminiski, “Initial Stiffness of Semi-Rigid Steel Beam-to-Column Connections,” Journal of Constructional Steel Research, Vol. 8, 1987. doi:10.1016/0143-974X(87)90054-X
- A. Azizinamini and J. Radziminiski, “Static and Cyclic Performance of Semi-Rigid Steel Beam-to-Column Connections,” Journal of Structural Engineering, Vol. 115, No. 12, 1989. doi:10.1061/(ASCE)0733-9445(1989)115:12(2979)
- N., Kishi and W. F. Chen, “Moment-Rotation Relations of Semi-Rigid Connections with Angles,” Journal of Structural Engineering, Vol. 116, No. 7, 1990.
- N. Kishi, W. F. Chen, K. G. Matsuoka and S. G. Nomachi, “Moment-Rotation of Top and Seat Angle with Double Web Angle Connections,” Proceeding of the Workshop on Connections and the Behaviour, Strength and Design of Steel Structures, Elsevier Applied Science, London, 1987a.
- N. Kishi, W. F. Chen, K. G. Matsuoka and S. G. Nomachi, “Moment-Rotation of Sigle-Double Web Angle Connections,” Proceeding of the Workshop on Connections and the Behaviour, Strength and Design of Steel Structures, Elsevier Applied Science, London, 1987b.
- J. Y. R. Liew, D. W. White and W. F. Chen, “Limit State Design of Semi-Rigid Frames Using Advanced Analysis: Part 1: Connection Modeling and Classification,” Journal of Constructional Steel Research, Vol. 26, No. 1, 1993, pp. 29-57. doi:10.1016/0143-974X(93)90066-2
- Y. L. Yee and R. E. Melchers, “Moment-Rotation Curves for Bolted Connections,” Journal of Structural Engineering, Vol. 112, No. 3, 1986, pp. 615-635. doi:10.1061/(ASCE)0733-9445(1986)112:3(615))
- A. S. Daryan, “A Study on Behavior of Connections in Fire,” MS Thesis, K. N. Toosi University, Tehran, 2006.
- A. S. Daryan and M. Yahyai, “Modeling of Bolted Angle Connections in Fire,” Fire Safety Journal, Vol. 44, No. 7, 2009, pp. 976-988. doi:10.1016/j.firesaf.2009.06.005





