Intelligent Control and Automation
Vol.09 No.02(2018), Article ID:84904,19 pages
10.4236/ica.2018.92002
Tensor-Centric Warfare I: Tensor Lanchester Equations
Vladimir Ivancevic1, Peyam Pourbeik2, Darryn Reid1
1Joint and Operations Analysis Division, Defence Science & Technology Group, Adelaide, Australia
2Cyber and Electronic Warfare Division, Defence Science & Technology Group, Adelaide, Australia
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 17, 2018; Accepted: May 27, 2018; Published: May 30, 2018
ABSTRACT
We propose the basis for a rigorous approach to modeling combat, specifically under conditions of complexity and uncertainty. The proposed basis is a tensorial generalization of earlier Lanchester-type equations, inspired by the contemporary debate in defence and military circles around how to best utilize information and communications systems in military operations, including the distributed C4ISR system (Command, Control, Communications, Computing, Intelligence, Surveillance and Reconnaissance). Despite attracting considerable interest and spawning several efforts to develop sound theoretical frameworks for informing force design decision-making, the development of good frameworks for analytically modeling combat remains anything but decided. Using a simple combat scenario, we first develop a tensor generalization of the Lanchester square law, and then extend it to also include the Lanchester linear law, which represents the effect of suppressive fire. We also add on-off control inputs, and discuss the results of a simple simulation of the final model using our small scenario.
Keywords:
Tensor Modeling of Complex Warfighting, Lanchester-Type Combat Equations, C4ISR Military System

1. Introduction
Since at least the time of the Military Enlightenment, military organizations have invested considerable effort into developing theories of war and battle. The purpose of such theories is ultimately to inform decisions: what equipment to acquire, what processes to institute, what training and education to develop, what research to conduct, how to conduct operations, and what operations to conduct in the first place. Perhaps unsurprisingly, many such efforts at the development of theories of war and battle have been oriented around the idea of achieving something like a complete and correct theory by which future outcomes might be predicted and thereby the means of determining the means to guarantee, or at least maximize the chances of, obtaining the outcome one desires. This has remained a dominant theme in military thinking ever since the foundational works of early theorists such as Jomini [1] , through adoptions into military domains other than land battles in the late 19th century and early 20th Century with military educators such as Mahan [2] , into the middle of the 20th Century with increasingly technologically-oriented theorists such as Fuller [3] [4] and Hart [5] , and into modern and even more heavily technologically focussed instantiations such as Network Centric Warfare (NCW) [6] and Effects-Based Operations (EBO) [7] . Classical attempts at mathematically modeling military conflict occurred within this overarching tradition of military thinking, and consequently they manifest the same basic goal of yielding mathematical theories that are numerically predictive with respect to battle outcomes.
Yet as predicted even from the outset by Clausewitz [8] , a programme aimed at developing theories predictive of outcomes is ultimately not possible, because―to use modern mathematical language―the conditions of war and battle are simply not ergodic. That is, the inherent complex nonlinearity of such systems yield strong limitations on what can be predicted about their outcomes; conditions are not static and distributions are not nicely behaved, making it not possible to sample from the unrealized future by collecting data about the past. As a result of his stance, Clausewitz set himself apart from both his contemporary Jomini and from most other military theorists since by shying away from fixed and prescriptive theories―while nonetheless conceding that such ideas are possible within sufficiently narrowly constrained problem domains. It is thus sometimes remarked that Clausewitz’ focus is strategic rather than tactical. More deeply, this point of view gives a basis that more methodologically focused than theory focused: we are here primarily concerned with the means of solving problems that are effectively unique, messy, under-specified, socially complex, evolving and for which there is generally a scarcity of available data. In other words, decision-making in military matters has all the characteristics of what are often now described as “wicked problems” [9] .
Against a broad backdrop where modern military organizations have sought to move away from approaching force development and employment from the point of view of individual platforms as collections of functions, theories such as NCW proved influential because they postulated that the ability of military organizations to collect and disseminate and process data while denying to adversaries the same ability is the crucial determiner of the outcome. The problem, however, is that NCW presented a discredited though intuitively appealing explanation for exactly how this is to occur, with practical consequences that have proven problematic [10] [11] ; its methodological framework held that knowledge is the outcome of collecting and consuming data and that the accuracy of the knowledge is a function of the amount of information and ability to process it. The slightly later EBO notion similarly concludes that information collection, dissemination and processing are crucial, yet arguably overstates the strength and usefulness for prediction of supposed connections between outcomes and ostensible causes. Therefore, instead of the NCW, we are talking about distributed C4ISR system (Command, Control, Communications, Computing, Intelligence, Surveillance and Reconnaissance); for one of its examples, see [12] .
These observations may be seen in terms of the limitations of classical systems engineering achievements in dealing with wicked problems [9] ; the remedy was a methodological shift to essentially the kind of problem-solving approach espoused and exemplified by Clausewitz, but fleshed out later by Popper and subsequent authors [13] [14] . This line of reasoning inspires our approach. As with most approaches to modeling combat, there can little doubt that connectivity is important, that the availability and quality of information matters; our explanation for why this is so departs from earlier methods in this that the networks at the heart of our model permit ideas to be tested more rapidly and more thoroughly. Thus we have in mind the ideas of problem-solving, where the problem choices are primarily of the wicked variety; it is not information per se that matters, but rather the ability to obtain information that reveals unacceptable error in proposed solutions and problem formulation. The goal of our modeling thus shifts from predicting outcomes of combat directly to questions about system control. In this paper and its successor we present a basis for a novel mathematical approach to modeling war and battle under the conditions of complexity and uncertainty as a step towards overcoming the limitations that have been so challenging to most models of combat outcomes proposed in the past.
2. Background
2.1. Lanchester Equations
In defence operation research community it is well known that classical Lanchester-Osipov combat equations (also called Lanchester-style mass action models [15] [16] [17] )1 include two forces, Red/Attacker’s strength: and Blue/Defender’s strength: , with their respective initial sizes and and their corresponding combat-effectiveness coefficients and . Lanchester equations are of the following two basic types:2
1) Lanchester square law for direct-aimed fire:
(2)
where overdot denotes time derivative, and and denote individual combat-rate coefficients for the Red and Blue forces, respectively (e.g., tank versus tank, concentration of fire).
2) Lanchester linear law for area―unaimed fire:
(3)
where and denote mixed combat-rate coefficients for Red and Blue forces (e.g., artillery barraging an area without precise knowledge of target locations).
Although similar Lanchester-type models had been extensively used in the past Century, today they are widely regarded as grossly oversimplified representations of modern warfare, at best. This motivates our effort towards a modeling methodology of much higher complexity, including both continuous and discrete spatiotemporal dynamics, as proposed in the present paper3.
2.2. Brief Review of Recent Military Thinking
For the last two decades, modern defence forces have generally been investing considerable effort in shifting the basis for decision-making for force development, employment and conduct of operations beyond individuation around platforms. Regarding ships, aircraft, armored vehicles and soldiers, for instance, as the base atomic units of military forces that are then packaged hierarchically yields separate Command and Control (C2) channels for different military functions, which are then attached to acicular organizations that necessarily centralism planning and coordination to achieve desired effects. The emergence of modern communications and information technology was consequently broadly seen as offering the potential to dissolve such crystalline arrangements in favor of military forces able to fluidly self-organize in rapidly changing situations to both counter threats and take advantage of opportunities, by enabling collaboration directly between elements formerly widely separated by hierarchy.
Other advances including those the fields of telecommunications, robotics, artificial intelligence and autonomous systems have further opened apparent opportunities for collaborative planning, coordination and rapid response; at its core, modern defence thinking seeks to achieve highly distributed C2 arrangements enabled by communications and information systems in which information can be rapidly disseminated while also being protected from outside interdiction and interference. The extreme instantiation of this lies in the idea that by the provision of such a system, together with the training and procedures to utilize it, “information superiority”―the ability to acquire, transport and process more information than the opposition―will deliver superior ability to apply the effects of military force, and thus at least maximum chances of winning, if not virtually guaranteed complete battlefield domination. The ability for foreseeable battlefield communication systems to provide an infrastructure sufficient to realism the required connectivity, the flawed nature of at least this kind of extreme account has been made manifest by the fact that apparently overwhelming forces, enjoying the full benefits of the best technology has to offer, can and do continue to lose to ostensibly backwards and inferior forces.
While there remains broad agreement that technological developments offer considerable opportunity, the issue of exactly what benefits are implied and how to best utilize the technologies to best effect have remained unsettled. Theories of war and battle intended as explanatory and predictive bases for guiding force development decision-making have been proposed―NCW being an especially prominent example in Western defence departments in the first decade of the 21st Century―but none has proven satisfactory. In the case of NCW, foundational problems with its explanation of methodology with far-reaching practical consequences in the design of systems and over-estimation of the relative benefits of the technology [10] , which have appeared to have been born out in practice, has left the theory much less enthusiastically received than in the heyday of its development. For present purposes, its weaknesses may be seen in terms of its inability to account adequately for command and control under conditions of uncertainty and complexity, now widely recognized in defence and military circles as a defining feature of combat; the theory is predicated on the notion that more information about past and present conditions leads to greater knowledge about future states, which, is known to be false in complex nonlinear systems [11] .
Recent years have seen a growing knowledge about, and interest in, the burgeoning knowledge across the sciences about complexity and uncertainty, among defence and military thinkers. The general emerging view is that defence and military matters feature burgeoning complexity of technological, social, economic, cultural and political varieties. Whether war and battle is really becoming more complex than in the past is highly debatable; what is more certain is that analytical and conceptual frameworks used in its study to inform force design decisions struggle to adequately account for effects that Clausewitz pondered 180 years ago. The objective of the present paper is to take a step in this direction by generalizing and making rigorous the study of information networks using tensor dynamics on battlespace manifolds, and integrating it with Lanchester-type attrition models.
3. System Input
3.1. From the Air Campaign Scenario to the Combat Tensor
To be able to compare our system with McLemore et al. [24] we need to have the same/similar system input and after computations to compare the outputs. In our scaled-down (toy) model we interpret their Table. Scenario forces, as follows. From a collaborative perspective, in their Air Campaign Scenario, the Red forces are given by a Bipartite graph: 15× Fighter aircraft and 15× Sensor aircraft, which in our 9 × 9-case becomes: 4 Fighter aircraft and 5 Sensor aircraft4 (see Figure 1). Also, their Blue forces are given by a Tripartite graph: 10× Fighter aircraft, 10× Sensor aircraft and 10× New aircraft, which in our 9 × 9-case becomes: 3 Fighter aircraft, 3 Sensor aircraft and 3 New aircraft (see Figure 2).
To make our Red and Blue aircraft configurations more realistic, the identity 9-matrices (with the local feedback-loops) have been added to the Red and Blue adjacency matrices as:
(4)
Figure 1. Bipartite graph for the Red force, including 4 Fighter aircraft and 5 Sensor aircraft.
Figure 2. Tripartite graph for the Blue force, including 3 Fighter aircraft, 3 Sensor aircraft and 3 New aircraft.
(5)
The graphs for our Red and Blue forces, defined by adjacency matrices with local self loops, and , respectively, are presented, using default graph embeddings in Mathematica®, in Figure 3 and Figure 4.
3.2. The Combat Tensors for the Red and Blue Forces
As a “soft” introduction to dynamics of vector and tensor fields on battlespace manifolds, we define here the Combat-tensors, as the following matrix products (i.e., tensor contractions):
Figure 3. Bipartite graph with local feedback loops for the Red force, including 4 Fighter aircraft and 5 Sensor aircraft.
Figure 4. Tripartite graph with local feedback loops for the Blue force, including 3 Fighter aircraft, 3 Sensor aircraft and 3 New aircraft.
of the combat adjacency matrices and with the total Power tensors and . Each component of the Power tensors (9 × 9 of them on the battle-manifold M9; see next section) is defined as a sum of the sigmoid spatiotemporal kink functions and .
4. TCW Battlespace
A set of all active and controllable degrees-of-freedom (DOFs) of an arbitrary complex system comprises the configuration manifold for that system (see [25] for more technical details). For example, an nD configuration manifold for a humanoid robot is the set of all its movable joint angles. Following this fundamental manifold prescription, any battlespace (see [26] and the references therein) in TCW can be formally defined as the battle-manifold. In case of a very large battle-manifold Mn, it can be approximated with , where n, the total number of DOFs, can be in millions (using computational framework outlined in the Appendix).
Complex warfighting dynamics on such battle-manifolds is naturally defined as an interplay of spatiotemporal vector and tensor fields flowing on them. For defining tensor expressions, we will use the abstract tensor notation with Einstein’s summation convention upon repeated indices; see [27] - [32] .
On any battle-manifold Mn we can observe a dynamic interplay of various Actors, all defined by various vector and tensor fields, depending on their complexity.
Simpler Actors are formally defined as spatiotemporal vector-fields, , similar to velocities and forces from classical mechanics, or flow-velocities and vortices from fluid mechanics, or Hamiltonian vector-fields from generalized mechanics [28] [29] , or Hopfield-Grossberg vector-fields from neurodynamics [33] .
The main Actors on any battle-manifold Mn are the Red and Blue vector-fields, and , respectively, which represent either the Red-Blue populations, or any other power measure of the Red-Blue forces.
The main supporting Actor is the combat-tensor , defined earlier, which belongs to this category; commutes with any other 2nd-order tensor field of the same covariance on the same battle-manifold Mn (e.g. )―they can be added together as linear machines:
All these tensor fields are spatiotemporal dynamical objects governed by tensor equations, similar to the elastic stress-strain relation: .
5. Tensor Combat Equations
5.1. Basic Tensor Combat Equations
For simplicity, we assume the simple 9D battle-manifold , coordinated by , although all the calculations would equally work for any
manifold dimension (up to millions, using the computational framework outlined in the Appendix). We start the TCW modeling with the tensor Lanchester square law, which is the following vector/tensor generalization of Equation (2):
(6)
where the Red and Blue forces are now defined as vector-fields, and , and their effectiveness coefficients are denoted by k and κ. The tensor fields and represent the sum of their combat-tensors ( and ), their total power (or stress-energy) tensors ( and ), and the Red and Blue swarming matrices, and from McLemore et al. [24] , provided the swarming matrices have dimension of :
For example, on a 9D battle-manifold M9, the basic tensor Lanchester Equation (6) expand as:
Similar expansions (though larger) hold for battle-manifolds of any dimensions and can be derived using the fast tensor package xTensor [34] for Mathematica®.
Assuming, for simplicity, the coordinate independence ( ), both sets of expanded Lanchester equations represent sets of coupled nonlinear ODEs, which can be directly numerically solved, for any given Red and Blue initial conditions: , , using any adaptive Runge-Kutta ODE-solver (e.g. Cash-Karp, Fehlberg and Dormand-Prince integrators), or their corresponding manifold/Lie-group integrators (e.g. Runge-Kutta Munthe-Kaas).
In the general case of explicit coordinate dependence ( ), we would be actually dealing with the set of the first-order nonlinear PDEs, which would all require spatial discretization (e.g., using the Method of Lines, as implemented in Mathematica), after which the above mentioned ODE-solvers can be used again.
The same computational algorithms will apply, in both cases (ODEs and PDEs), also for the extended tensor Lanchester equations, formulated as follows.
5.2. Adding the Lanchester Linear Law
Next, to include the Lanchester linear law Equation (3) into Equation (6), while keeping their covariance (so that each term represents a vector-field), we need to extend them with quadratic terms of the Lanchester unaimed-fire equations (linear law) as:5
(7)
where the fourth-order tensors and represent more complex, strategic, tactical and operational, Red and Blue capabilities, which can be defined either as the outer products of various matrices from [24] , or composed as triple tensor sums:
(8)
The basic Red and Blue tensor combat Equation (7) are implemented in Mathematica as the initial value problem for the following temporal vector-fields:
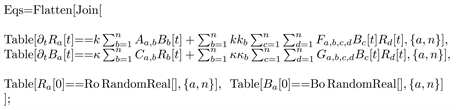
where the 2nd-order Red and Blue combat-tensors and are defined via sparse adjacency matrices (4) and (5) as:
and the 4th-order (strategic + tactical + operational) tensors and are defined as:
A sample simulation of the basic tensor combat Equation (7) is performed in Mathematica (see Figures 5-7) for 10 time units (to match the simulations given in [24] ) and random initial conditions.
5.3. Interpretation of Dynamical Simulations
The focus of our interpretation is the Red-Blue dynamics phase plot in Figure 7. This illustrates nine instances of engagement between the Red and Blue forces, confirming a fully engaged scenario. Figure 5 and Figure 6 are indicators of the outcome of the engagements: Blue is clearly winning in seven instances (note the exponential-like growth seen in Figure 6). On the other hand, Red is only winning in two of the engagements. It should be noted that one of the engagements seems to be border line or not clear, which is indicative of the uncertainty of the outcome of this specific instance of engagement. The warfare uncertainty will be addressed in [25] .
Figure 5. Sample simulation of the basic tensor combat Equation (7) for 10 time units with random initial conditions: monotonic dynamics of Red forces.
Figure 6. Sample simulation of the basic tensor combat Equation (7) for 10 time units with random initial conditions: monotonic dynamics of Blue forces.
Figure 7. Sample simulation of the basic tensor combat Equation (7) for 10 time units with random initial conditions: monotonic Red-Blue phase plots.
In contrast, the output from [24] presented in their Chart 1 (Blue) and Chart 2 (Red) does not show the actual dynamics of the simulation, but rather the statistical inference from that simulation. Their main point is the “kill” of the aircraft, which they plotted along the same time axes (10 units) that we are using for the simulation. The 9 conflict points in our phase plane (Figure 7) are the points of potential “kill”; by relating to the Red and Blue time evolutions (in Figure 5 and Figure 6) we can also infer who was “killed” or “degraded” at that same time point, as compared to their Chart 1 and Chart 2.
Based on this interpretation, we can see that our proposed tensor framework is capable of addressing the similar questions as those addressed by [24] . In the subsequent paper [25] we will extend this tensor Red-Blue dynamics to model warfare uncertainty.
5.4. Adding Bang-Bang Control Actions
For the purpose of recasting the combat-dynamics Equations (7) into a control system, we will add to both Red and Blue forces simple-and-strong bang-bang (on-off) control inputs and of the form:
where is the total simulation time (in our case time units, to match the scenario from [24] ).
In this way, we obtain the controlled tensor Red-Blue equations:
(9)
The basic vector control inputs and are implemented in Mathematica (in the scalar form) as:
Which gives the implementation of the controlled Red-Blue Equations (9) as:
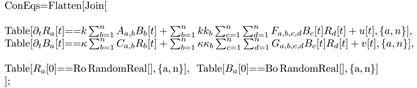
A sample simulation of the bang-bang controlled tensor combat Equation (9) is performed in Mathematica (see Figures 8-10) for 10 time units and random initial conditions.
From Figures 8-10 we can see that adding strong bang-bang control inputs to tensor combat equations completely changes the natural combat-dynamics behavior―control actions have the overall flattening effect. Even if the control inputs have lower amplitudes (e.g., 5 instead of 10) the outcome would be qualitatively similar: both the time-plots and the phase plot would be flattened out. From these computational observations we can infer that adding artificial control inputs to natural Red-Blue combat dynamics does not make real sense, because in reality the Red and Blue forces mutually control each other.
6. Conclusion and Future Work
We have presented the basic development of the tensor-centric warfare (TCW),
Figure 8. Sample simulation of the bang-bang controlled tensor Equation (9) for 10 time units with random initial conditions: dynamics of Red forces.
Figure 9. Sample simulation of the bang-bang controlled tensor Equation (9) for 10 time units with random initial conditions: dynamics of Blue forces.
Figure 10. Sample simulation of the bang-bang controlled tensor Equation (9) for 10 time units with random initial conditions: Red-Blue phase plots.
as a tensor union and generalization of classical Lanchester combat equations and modern intention to orient the conduct of defence and military decision-making around functions that cross traditional hierarchical lines of command. Recognizing both the debates that continue about how best to do this and the limitations and weaknesses in military theories intended to inform and drive these developments, we have picked up the central feature of information and communications systems as a base infrastructure in future force design. The emphasis in our formalization lies in the possibility of better addressing the complexity and uncertainty inherent in war and battle, which, despite having been studied since the Military Enlightenment period, have continued to prove challenging to military thinking. In the sequel to this paper, presented in [25] , we are extending this basic development with entropic modeling of warfare uncertainty and symmetry.
Acknowledgements
The authors are grateful to Dr. Tim McKay and Dr. Brandon Pincombe, Joint and Operations Analysis Division, Defence Science & Technology Group, Australia―for their constructive comments which have improved the quality of this paper.
Cite this paper
Ivancevic, V., Pourbeik, P. and Reid, D. (2018) Tensor-Centric Warfare I: Tensor Lanchester Equations. Intelligent Control and Automation, 9, 11-29. https://doi.org/10.4236/ica.2018.92002
References
- 1. Jomini, A.H. (2007) Baron de: The Art of War (Dover Edition). Dover Publications, New York. (First Published in 1862)
- 2. Mahan, A.T. (2003) The Influence of Sea Power upon History: 1660-1783. Pelican Pub. Co., Gretna. (Original Publication 1890)
- 3. Fuller, J.F.C. (1926) The Foundations of the Science of War. Hutchinson and Company, London. https://archive.org/details/foundationsofsci00jfcf
- 4. Fuller, J.F.C. (1942) Machine Warfare: An Enquiry into the Influence of Mechanics on the Art of War. Hutchinson, London.
- 5. Hart, B.H. (1967) Liddell: Strategy. 2nd Revised Edition, Fredrick A. Praeger Publishers, New York.
- 6. Alberts, D., Garstka, J. and Stein, F. (1999) Network Centric Warfare: Developing and Leveraging Information Superiority. CCRP.
- 7. Davis, P.K. (2002) Effects-Based Operations: A Grand Challenge for the Analytical Community. RAND Corporation, Santa Monica, Arlington, and Pittsburgh.
- 8. von Clausewitz, C. (1989) In: Howard, M. and Paret, P., Eds., On War, Princeton University Press.
- 9. Rittel, H. and Webber, M. (1973) Dilemmas in a General Theory of Planning. Policy Sciences, 4, Elsevier, Amsterdam, 155-169. (Reprinted in Cross, N., Ed. (1984) Developments in Design Methodology, Wiley and Sons, Chirchester.)
- 10. Reid, D.J., Goodman, G., Johnson, W. and Giffin, R.E. (2005) All That Glisters: Is Network-Centric Warfare Really Scientific? Defense and Security Analysis, 21, 335-367. https://doi.org/10.1080/1475179052000345403
- 11. Reid, D.J. (2017) An Autonomy Interrogative. In: Abbass, H.A., Scholz, J. and Reid, D.J., Eds., Foundations of Trusted Autonomy, Springer, New York, 365-391.
- 12. Hui, P.P. (2011) OPAL—A Survivability-Oriented Approach to Management of Tactical Military Networks. IEEE Military Communications Conference. https://doi.org/10.1109/MILCOM.2011.6127450
- 13. Popper, K. (2014) Conjectures and Refutations: The Growth of Scientific Knowledge. Routledge, New York (First Published in 1963).
- 14. Miller, D. (1998) Critical Rationalism: a Restatement and Defence. Open Court.
- 15. Lanchester, F.W. (1916) Aircraft in Warfare: The Dawn of the Fourth Arm. Constable, London.
- 16. Lanchester, F.W. (2000) Mathematics in Warfare. In: Newman, J., Ed., The World of Mathematics, Vol. 4, Simon and Schuster, New York, 2138-2157.
- 17. Osipov, M. (1995) The Influence of the Numerical Strength of Engaged Forces on Their Casualties. In: Helmbold, R.L. and Rehm, A.S., Trans., Warfare Modeling, Military Operations Research Society, John Wiley & Sons, Hoboken, 290-343.
- 18. Chase, J.V. (1902) Sea Fights: A Mathematical Investigation of the Effect of Superiority of Force in Combats upon the Sea. Naval War College Archives, RG 8, Box 109, XTAV.
- 19. Fiske, B.A. (1905) American Naval Policy. U.S. Naval Institute Proceedings.
- 20. Baudry, A. (1912) La Bataille navale: Etudes sur les facteurs tactiques [The Naval Battle: Studies of the Tactical Factors]. Translated by C. F. Atkinson, Hugh Rees, London.
- 21. Peterson, R. (1967) On the Logarithmic Law of Combat and Its Application to Tank Combat. Operations Research, 15, 557-558. https://doi.org/10.1287/opre.15.3.557
- 22. Bracken, J. (1995) Lanchester Models of the Ardennes Campaign. Naval Research Logistics, 42, 559-577. https://doi.org/10.1002/1520-6750(199506)42:4<559::AID-NAV3220420405>3.0.CO;2-R
- 23. Keane, T. (2011) Combat Modelling with Partial Differential Equations. Applied Mathematical Modelling, 35, 2723-2735. https://doi.org/10.1016/j.apm.2010.11.057
- 24. McLemore, C., Gaver, D. and Jacobs, P. (2016) A Model for Geographically Distributed Combat Interactions of Swarming Naval and Air Forces. Naval Research Logistics, 63, 562-576. https://doi.org/10.1002/nav.21720
- 25. Ivancevic, V., Reid, D. and Pourbeik, P. (to appear) Tensor-Centric Warfare II: Entropic Uncertainty Modeling. ICA.
- 26. Wikipedia (2017) Battlespace.
- 27. Penrose, R. (2004) The Road to Reality. Jonathan Cape, London.
- 28. Ivancevic, V. and Ivancevic, T. (2006) Geometrical Dynamics of Complex Systems. Springer, Dordrecht. https://doi.org/10.1007/1-4020-4545-X
- 29. Ivancevic, V. and Ivancevic, T. (2007) Applied Differential Geometry: A Modern Introduction. World Scientific, Singapore. https://doi.org/10.1142/6420
- 30. Ivancevic, V. and Ivancevic, T. (2008) Complex Nonlinearity: Chaos, Phase Transitions, Topology Change and Path Integrals. Springer, Berlin.
- 31. Ivancevic, V. and Reid, D. (2015) Complexity and Control: Towards a Rigorous Behavioral Theory of Complex Dynamical Systems. World Scientific, Singapore.
- 32. Ivancevic, V., Reid, D. and Pilling, M. (2017) Mathematics of Autonomy: Mathematical Methods for Cyber-Physical-Cognitive Systems. World Scientific, New Jersey/Singapore.
- 33. Ivancevic, V. and Ivancevic, T. (2007) Neuro-Fuzzy Associative Machinery for Comprehensive Brain and Cognition Modelling. Springer, Berlin. https://doi.org/10.1007/978-3-540-48396-0
- 34. xTensor (2015) Fast Abstract Tensor Computer Algebra. http://xact.es/xTensor/
- 35. EurekAlert! (12 June 2017) Blue Brain Team Discovers a Multi-Dimensional Universe in Brain Networks.
- 36. Reimann, M., et al. (2017) Cliques of Neurons Bound into Cavities Provide a Missing Link between Structure and Function. Frontiers in Computational Neuroscience, 11, 48. https://doi.org/10.3389/fncom.2017.00048
- 37. Bassett, D. and Sporns, O. (2017) Network Neuroscience. Nature Neuroscience, 20, 353-364. https://doi.org/10.1038/nn.4502
- 38. Bauer, U., Kerber, M., Reininghaus, J. and Wagner, H. (2017) PHAT—Persistent Homology Algorithms Toolbox. Journal of Symbolic Computation, 78, 76-90. https://doi.org/10.1016/j.jsc.2016.03.008
- 39. (2017) AD: Automatic Differentiation. Hackage. https://hackage.haskell.org/package/ad
- 40. DiffSharp (2017) Differentiable Functional Programming. http://diffsharp.github.io/DiffSharp/
Appendix: Computational Framework
A network-computational framework, with networks/tensors of up to millions of nodes, can be developed using the publicly available Matlab® toolbox supporting the cutting-edge topological research of brain cliques and cavities from computational neuroscience (the Blue Brain project [35] [36] [37] ). It is based on the persistent homology algorithms on directed simplices [38] .
All tensor expressions can be derived using the tensor package xTensor [34] for Mathematica. After Mathematica derivation, all tensor expressions can be completely evaluated (for manifolds of any dimension) using quasi-symbolic gradients computed by automatic differentiation, implemented either in C++, or in functional languages like Haskell (AD library) [39] and/or F-sharp (DiffSharp library) [40] .
NOTES
1We remark that before Lanchester and Osipov, similar mass action models in naval applications were proposed by Chase [18] , Fiske [19] and Baudry [20] .
2Frequently used generalization of the classical Lanchester-Osipov models of combat force dynamics [15] [16] [17] ―including two forces, Red/Attacker’s strength: and Blue/Defender’s strength: , with their respective initial sizes and and their corresponding combat-effectiveness coefficients and ―is the LPB model, proposed in 1960s by Peterson [21] and in 1990s by Bracken [22] , which reads:
(1)
where the exponents p and q (such that ) need to be empirically determined. The conserved quantity in the LPB model (1), is obtained by eliminating time t, separating and integrating. The Lanchester aimed-fire (or, square law) model:
corresponds to and thus to ; and the unaimed-fire (or, linear law) model:
corresponds to and thus in the LPB model (1) (for more technical details see, e.g. [23] and the references therein).
3Since we will be using tensor indices (subscripts and superscripts) and Einstein’s summation convention over repeated indices, to avoid confusion, we will focus on Lanchester’s own models (2)-(3), rather than on the LPB model with exponents (1).
4Since we have a simplified 9 × 9-case, we do not have the same number of Fighter and Sensor aircraft, and from the collaborative decision-making perspective sensors are more important than fighters. In recent military operations, there has been anecdotal evidence that access to larger number of sensors has great effect on the outcome.
5The Basic Red and Blue tensor combat Equations (6)-(7) are valid for any linear/flat manifold M9. In case of a strongly nonlinear/curved manifold M9, they would need the additional connection coefficients (i.e., Christoffel symbols)―which can be neglected for our purpose, as an unnecessary over-complication. With this view in mind, in the following sections we will introduce more complex dynamics and nonlinear control concepts into Equations (6)-(7), without introducing any geometric connection (e.g., Levi-Civita connection on Riemannian manifolds)―which can always be added to the battlespace system as additional nonlinear complexity (see [30] ).











