Received 21 April 2016; accepted 11 July 2016; published 14 July 2016

ABSTRACT

This paper proposes the continuous controller design method for quantum Shannon entropy, which can continuously drive the entropy to track a desired trajectory. We also analyzed the controllability of Shannon entropy in very short time interval. Simulations are done on five dimensional quantum system, which can verify the validation of the method.

Keywords:

Quantum Control, Quantum Information, Quantum Entropy

1. Introduction

Quantum control has become an important topic in quantum information [1] [2] , molecular chemistry [3] and atom physics [4] . Several control methods, including optimal control [5] , Lyapunov control [6] , learning control [7] , feedback control [8] and incoherent control [9] [10] , have been used to controller design of quantum systems. Quantum entropy control is one of the twenty open problems in quantum control [11] . In the 2012 “Quantum Characterization, Verification and Validation Workshop” in Bethesda, a group of scientists discussed about some typical questions like how to build a quantum device. The consensus at this workshop is that our common goal should be to somehow master a quantum system’s entropy, thereby enabling smooth sailing towards our final destination of full-scale quantum computers.

For pure state in closed quantum systems, our previous work [12] proposed the discretized controller design method for Shannon entropy. This paper proposes the continuous Shannon entropy controller, which can achieve quite accurate control effect. In control theory, accurate tracking control is a very difficult question. And for quantum systems, if the entropy can be tracked continuously, we can make the control effect more accurate. The discretized controller can be regarded as a simplified version of the continuous controller. The continuous controller can drive a quantum system’s entropy to accurately track a desired trajectory. The controllability of continuous control is hard to explore, and in this paper we briefly introduce the controllability analyzing methods which give the necessary and sufficient conditions of controllability in very short time period. Such analysis can overcome the weakness of previous discretized controller, and provide a new perspective of accurate tracking for both quantum and classical systems.

This paper is organized as follows. Section 2 shows the definition of quantum Shannon entropy, and presents our control goal. Section 3 provides the continuous controller design methods. Section 4 shows the numerical simulation examples. Concluding remarks are given in Section 5.

2. Preliminary

In quantum control, the state of a closed quantum system is represented by a state vector (wave function) 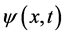in a Hilbert space. Here for the space variable we only consider one dimensional position variable x. The evolution of the state obeys the Schrödinger equation

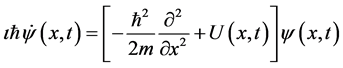(1)

where, and the external potential field 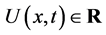is taken as the control term. For an infinite dimensional quantum system, the wave function is the superposition of free Hamiltonian’s eigenstates: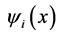

(2)

where both the wave function and the coefficients should be normalized:

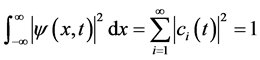(3)

Defining the state of the system as

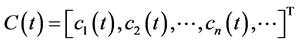(4)

we can get the state space control mode

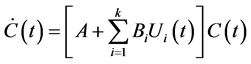(5)

where both A and 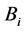are skew-Hermitian matrices. If the case with only one controller can be well solved, it will be easier for multiple-controller cases. So this paper only considers the following case with one controller:

(6)

Assuming a system that consists of n states, in which the probability for the i-th state to happen is, the traditional Shannon entropy in information theory is defined as

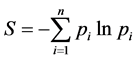(7)

which shows the degree of randomness of the system. For example, when, every state happens in the equal probability, which is a random system. In this situation, the Shannon entropy takes its maximum value. If, the system is completely predictable, i.e., the first state always happens and the entropy takes its minimum value 0. We can also regard the entropy as the superposition of the uncertainties because larger probability leads to smaller uncertainty. Similarly, the quantum Shannon entropy can be defined as

(8)

where is the probability that the superposition state collapses to the i-th eigenstate upon quantum measurement. From definition (8) we know, the entropy satisfies. For n-level quantum systems,

reaches its maximum value when, and reaches its minimum value 0 when

(9)

where k is a given integer. Here is defined as 0, which can be seen from

(10)

Our control goal is to drive the entropy to track a desired trajectory. The control of can be realized by controlling the probability density. In Section 3 we provide the method which can directly drive the entropy to track a desired trajectory.

3. Continuous Controller Design

Here we provide the continuous controller design method which can drive the entropy (8) to track a desired trajectory. Such control task is called “temporal control”, which means not only the destiny should satisfy the requirement, but also the entropy at any instant of the entire process should follow the pre-specified value.

Here we only consider finite-dimensional quantum systems with dimension n. First we can get the time derivative of (8) as

(11)

where

(12)

because the sum of probabilities should always equal 1. So we have

(13)

Here we use and to denote real part and imaginary part, respectively. We can define a row vector

(14)

which leads to

(15)

Here “” denotes the Hadamard product which means the corresponding elements are multiplied:

(16)

Next we define

(17)

which gives

(18)

So we can get the controller

(19)

If the desired trajectory of is known, then at any time we can use (19) to calculate the feedback controller. We can combine (6) and (19) together to solve the controller out without measuring, so such method belongs to open-loop control. When holds, it is always easy to use (19) to make the entropy track the desired trajectory. When, there may not exist proper controller which can drive the entropy along the prescribed trajectory. Such singularity problem can be dealt with by the singularity managing approaches used in quantum tracking control. The singularities can be divided into two types: trivial and nontrivial. A trivial singularity refers to the case that remains zero for a long time; a nontrivial singularity means that is zero only at some isolated points on the tracking trajectory. The singularities can also be classified as removable and intrinsic according to their controllability characteristics. For removable singularities, the track passing through the singular points can still be followed and a finite control field can be determined by appropriate numerical algorithms; for intrinsic singularities, the track can not be exactly followed. Note that the type of removable or intrinsic is irrelevant to triviality. A trivial (or nontrivial) singularity could be a removable or intrinsic type. For trivial but removable singularity which means the system is controllable, the field can be obtained by taking higher order time derivatives of (19) until the singularity is removed. For nontrivial singular points, the field could have the form of either (i) or (ii). For case (i), the field does not have a finite value and the system is uncontrollable at those points (i.e., a nontrivial but intrinsic singularity type). The occurrence of case (i) is most likely due to an overdemanding prescribed track. For case (ii), usually after applying L’Hopital’s rule, the field will have a finite value at the point and the system is still controllable (i.e., a nontrivial but removable singularity type). However, if L’Hopital’s rule needs to be applied many times, or if the field has a very large value, in practice it could be very difficult to perform accurate tracking. For both cases, an attractive alternative would be an alteration of the originally prescribed track in an attempt to circumvent or overcome the singular behavior while still meeting the target goal at the end of the track. We can use an alternative trajectory which can achieve satisfactory result in some particular example. For uncontrollable systems, such algorithm will trigger endless switching to different tracks without achieving good control. In order to avoid too strong control requirement which makes the tracking ill-posed, further study can be done on the controllability issue. Next we provide the necessary and sufficient conditions under which the entropy can only increase (or decrease) in very short time, which can give helpful instruction to the prescribed track’s selection.

When, there is possibility that in very short time, the entropy can only increase or decrease. In order to analyze the controllability when, we first show the following proposition about the derivatives of both and.

Proposition 1. When holds, we have

where

and is defined as

.

Proof. From (18) we can get

where, and can be calculated as follows:

So we have

Hence Proposition 1 has been proved. □

Based on Proposition 1, we can get the conditions under which in very short time the entropy can only increase or decrease, which are shown in Theorem 1. It can be seen that Theorem 1 gives the necessary and sufficient conditions.

Theorem 1. In very short time, the entropy can only increase when

or or

and can only decrease when

or or

Proof. Assuming the sampling period is T, can be descretized as

,

which gives

.

Similarly we can get

.

If remains constant as in the first sampling period T, can be approximated as

Here is a once basic quadratic equation about, and the equation’s discriminant can be calculated as

.

If, we have. So it is always easy to find to make positive or negative, which means in very short time the entropy can both increase and decrease.

If, we can get, which yields. If, we have, which means in very short time the entropy can only increase; similarly if, the entropy can only decrease; if, we have

.

Here is also a once basic quadratic equation about, and the equation’s discriminant can be calculated as

.

When, we have, which means the entropy can both increase and decrease; when, the discussion can be divided into 3 cases:

(a) If, the parabola opens upward, which means the entropy can only increase.

(b) If, the parabola opens downward, which means the entropy can only decrease.

(c) If, we have, which gives and. So when, the entropy can only increase; when, the entropy can only decrease; when, the entropy will remain constant in very short time.

Above all, we can get the conclusion in Theorem 1. □

In quantum mechanics, A is often chosen to be diagonal, thus all the elements in A are pure imaginary since A is skew-Hermitian. Assume, where holds. We can get

(20)

From (18) we can see, which gives So we can get the controller

(21)

When, if the desired trajectory of is known, we can simply use (21) to get the controller. When, the conditions under which in very short time the entropy can only increase or decrease are shown in Theorem 2.

Theorem 2. If A is diagonal, in very short time the entropy can only increase when

and can only decrease when

Proof. From we know. So when, it is always easy to choose to make positive or negative. When, we can get

.

The discussion can be divided into 3 cases:

(a):

We have. If, it is easy to choose to make positive or negative; if, the entropy will remain constant in very short time.

(b):

Here is also a once basic quadratic equation about, and the equation’s discriminant can be calculated as. If, we have, which means the entropy can only increase; if, we have, which means the entropy can both increase and decrease in very short time.

(c):

Similarly we know if, the entropy can only increase; if, the entropy can both increase and decrease in very short time.

Above all, we can get the conclusion in Theorem 2. □

When the entropy has reached the target, it needs to be maintained constant. If A is diagonal, from (21) we know we only need to maintain the entropy constant. If A is non-diagonal, it is difficult to keep the entropy constant especially when there exists disturbance. Then we need the discrete control method in Section 4 to overcome the disturbance.

4. Simulations

We present simulations for continuous controller on a five-level quantum system. For the five-level case in which the discrete controller is difficult to apply, the continuous controller is adopted to achieve good performance, and the controllability result is verified by simulation.

For five-level quantum system

(22)

the discrete controller is difficult to apply, while the continuous controller can be adopted to achieve good performance. For initial state with, we expect that the entropy

changes as follows in seven steps: (a) increases to 1.61; (b) keeps constant; (c) increases to 1.66; (d) keeps constant; (e) decreases to 1.61; (f) increases to 1.66; (g) keeps constant. If, the controller can be calculated by (8) as

(23)

Combining (22) with (23) we can get the simulation results for both and, which are shown in Figure 1.

From Figure 1 we can see that for the five-level case which is difficult to apply the discrete controller, the

continuous method can lead to very accurate tracking. At some instant may be 0, and such derivative discontinuing may prevent precise tracking in the vicinity of the switch point. In practice the most important issue is to keep the tracking process under good control before and after switching. And the simulation shows that the entropy can still be driven to go along the desired trajectory.

Next we verify the controllability result by simulation. For initial state with, since it satisfies and, from Theorem 2 we know the entropy can only increase in very short time. The change of entropy with respect to at time T under different are shown in Figure 2. For larger, T should be smaller to guarantee the accuracy. Here we choose

where is the floor function which denotes the maximum integer which is not more than x. For example, when,

From Figure 2 we can see that no matter how large is, the entropy can only increase at the beginning, which coincides with Theorem 2.

5. Conclusion

This paper proposed the continuous controller design method for quantum Shannon entropy. Different from our previous work on discretized controller, the new method can continuously drive the entropy to track a pre-specified target trajectory. Controllability analysis is also provided. The simulation results verified the validation of the method.

Acknowledgements

This work is supported by the Postdoctoral International Exchanging Program of China.

Cite this paper

Yifan Xing,Wensen Huang,Jinhui Zhao, (2016) Continuous Controller Design for Quantum Shannon Entropy. Intelligent Control and Automation,07,63-72. doi: 10.4236/ica.2016.73007

References

NOTES

^*Corresponding author.