Intelligent Control and Automation
Vol.06 No.04(2015), Article ID:60844,9 pages
10.4236/ica.2015.64020
A Novel Technique for Detection of Time Delay Switch Attack on Load Frequency Control
Arman Sargolzaei1, Kang K. Yen1, Mohamed N. Abdelghani2, Abolfazl Mehbodniya3, Saman Sargolzaei4
1Department of Electrical and Computer Engineering, Florida International University, Miami, FL, USA
2Department of Mathematics and Statistics, University of Alberta, Edmonton, Canada
3Graduate School of Engineering-Sendai, Tohoku University, Sendai, Japan
4Department of Electrical and Computer Engineering, Wentworth Institute of Technology, Boston, MA, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 7 August 2015; accepted 27 October 2015; published 30 October 2015

ABSTRACT
In this paper, we focus on the estimation of time delays caused by adversaries in the sensing loop (SL). Based on the literature review, time delay switch (TDS) attacks could make any control system, in particular a power control system, unstable. Therefore, future smart grids will have to use advanced methods to provide better situational awareness of power grid states keeping smart grids reliable and safe from TDS attacks. Here, we introduce a simple method for preventing time delay switch attack on networked control systems. The method relies on an estimator that will estimate and track time delays introduced by an adversary. Knowing the maximum tolerable time delay of the plant’s optimal controller for which the plant remains stable, a time-delay detector issues an alarm signal when the estimated time delay is larger than the minimum one and directs the system to alarm state. In an alarm state, the plant operates under the control of an emergency controller that is local to the plant and remains in this mode until the networked control system state is restored. This method is an inexpensive and simple way to guarantee that an industrial control system remains stable and secure.
Keywords:
Time Delay Switch Attack, Load Frequency Control, Detection and Estimation, Emergency Controller

1. Introduction
Modern power grids rely on telecommunication technologies for control and monitoring, in a way to improve efficiency and reliability distribution. However, their reliance on computers and multi-purpose networks makes them vulnerable to cyber-attacks [1] -[3] . Recently, the investigation of attack methods on industrial control systems and their countermeasures have been the focus of many academic, industries, and governments. Here, we will investigate one type of attacks on a power control system recently proposed by Sargolzaei et al. [4] -[6] that is time delay switch attack and we provide a simple detection/estimation technique for time delays caused by an adversary. State estimation is one of the pivotal features of future power systems [7] . According to [8] , improving the resiliency and reliability of smart distribution networks could be obtained via deploying renewable resources and demand side management programs. As it has been mentioned in [9] , demand response can ameliorate the load curve by motivating smart customers utilizing smart communication infrastructure and smart meters.
The controller design for systems with time delay is one of the interests of many researchers [10] -[12] but they have not studied that time delay can be injected to the system as an attack. Time delays injected by a hacker in a control system would, in general, destabilize the system or cause inefficiency in performance of the system. This is a new attack in the context of power systems (e.g., load frequency control (LFC)) on networked control systems (NCS) [13] and is named time-delay-switch attack or TDS for short [4] . To avoid possible damage of TDS attacks, systems and controllers must be redesigned in a way to detect and correct for variable time delays.
Time delays exist in power systems, in the sensing and control loops. The traditional controllers of power systems are designed based on current information being available and ignoring time delays even if they present. However, power grids technologies are continuously being improved by introducing new telecommunication technologies for monitoring to improve efficiency, reliability and sustainability of supply and distribution. For example, the introduction of a wide area measurement system (WAMS) provides synchronized near real-time measurements in phase measurement units (PMUs). WAMS which are used for stability analysis of power systems can also be used for designing more robust controllers. Nevertheless, time delays are present in PMUs measurements as a result of natural transmission lines [14] .
Several studies have considered the problem of stability of power systems with time delays [10] [11] . The impact of time delays on the power system controllers was discussed in [15] -[19] . In [20] , authors studied the effects of delays on the small signal stability of power systems. In [15] and [16] , methods to eliminate oscillations that resulted from time-delayed feedback control were proposed. Authors in [21] presented a wide-area control system for damping generator oscillations. Using phasor measurements, but with delays, a controller was proposed in [14] and small signal stability of the power system was considered. A feedback controller designed for power systems with delayed states was proposed in [22] . This controller deals with the combined effects of the instantaneous as well as delayed states using the quadratic Lyapunov function for systems with delays. Additional studies on power systems with delay can be found in [2] [3] [10] -[12] [23] -[25] and the references therein. However, most of these studies considered either the construction of controllers that were robust to time delays or controllers that used offline estimate of time delays. As far as we know, there are no control methods that perform online estimation of dynamic time delays and real time control of power systems. Furthermore, few studies [26] [27] considered control of power systems with time delays introduced by adversary.
In this paper, we will describe a simple yet effective method to address a TDS attack on the observed states of a controlled system. Our method utilizes a time delay estimator, a communication protocol to alarm for time delay switch attack, a buffer to store the history of controller commands and an optimal controller to stabilize or track a reference signal and a local to the plant emergency controller to stabilize the plant if large time delays are detected. For now, we will only deal with LTI systems in state feedback.
2. Method
All control methods developed in the past compensate for time delays either rely on controller robust to a maximum time delay, off-line estimates of time delays or approximation of time delayed signals [26] [27] . Here, we develop an alternative time delay estimator which is simpler and will help with systems under time delay attack. In this paper, we propose a general method for control of systems under TDS attack. We have developed this method for continuous linear time-invariant systems. We have implemented our models and control strategies in MATLAB to demonstrate the performance with simulation.
The proposed method is shown in Figure 1. Its basic elements are: plant model, time delay detector, emergency controller and controller. The controller can either be a PID controller or an optimal feedback controller. The emergency controller’s job is to stabilize the system in case of an attack on the communication lines of the distant controller. The time delay detector estimates the time delay in the communication channel from telemetered data. If the delay is larger than a maximum allowed time delay it sends alarm signals to the controller and emergency controller. If an alarm signal is received by the emergency controller it will begin to operate in a way to stabilize the plant to a desired state while the distant controller stops to operate until the delay is corrected.
Suppose the system we are dealing with is linear time invariant (LTI) or can be approximated in a region of interest by a LTI system,
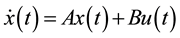 , (1)
, (1)
where x and u are state and control vectors, respectively. Matrices A and B are constant matrices with suitable dimensions.
Then, the solution is given by
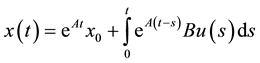 (2)
(2)
with time delay τ, either a time-delay switch attack or a natural delay, the solution of Equation (2) becomes
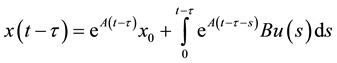 . (3)
. (3)
Let us write the solution 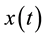 at the time t in terms of the solution with the time delay
at the time t in terms of the solution with the time delay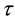 ; we have
; we have
 (4)
(4)
In general, the time delay τ is an unknown variable. Let’s assume that τ is slowly varying, compared to the changes in u and x, and 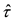 is our estimate of the time delay τ. Then,
is our estimate of the time delay τ. Then, 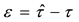 is the estimation error in the time delay. The predicted state
is the estimation error in the time delay. The predicted state 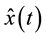 of the system based on the estimate of time delay
of the system based on the estimate of time delay 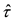 is given by
is given by
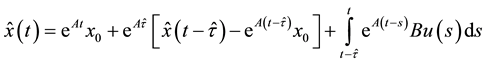 (5)
(5)
where 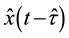 is the estimate of the delayed state given the estimate of the delay
is the estimate of the delayed state given the estimate of the delay  (i.e. a simulated signal).
(i.e. a simulated signal).
It should be noted that, 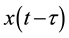 is what we actually measures and deliver to the plant model. So, at every instance of time, the variables
is what we actually measures and deliver to the plant model. So, at every instance of time, the variables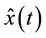 ,
, 






Figure 1. Block diagram of the proposed control system.
The estimation error in states can be described by 

Then the idea is to estimate 


where 


Assuming that, 

Equation (9) is the one we will use to estimate the time delay



After designing the time delay estimator, we turn our attention to the controller and emergency controller. The controller can either be a PID controller or an optimal controller depending on the requirements of the application. Equation (10) is the PID controller and Equation (11) is the optimal controller,


where the error is

Suppose there is a time delay attack on the system with delay


where c is a constant between 0 and 1. In case D = 1 an alarm signal is sent to the controller to shut it down and a negative acknowledgement is sent to the emergency controller to stabilize the plant. The control strategy is shown in Figure 1.
We have implemented this method in MATLAB and verified its performance using the load frequency control (LFC) of a two-area distributed power system. In the next section we present and discuss the simulation results.
3. Result
We focus on the LFC system where the controller’s function is to regulate the states of a networked power plant. The multi interconnect LFC dynamic system description can be found in [4] . Here we focus on two-area power system with the attack model as

The optimal feedback controller is given by

and the new state after the attack can be modeled by

where 

all zero, the system is in its normal operation. An adversary can get access to the communication link and inject a delay attack on the line to direct the system to abnormal operations.
In (13), 


where




nerator, position value of the turbine, tie-line power flow, and control error on the 


where 
In the dynamic model of the two-area LFC (13):



and






and

where i and j can only be values one and two, 








The analysis starts with the design of an optimal controller for the LFC in the normal operation (i.e., with no attack). Consider the system model described by (13) with the performance index described by

where matrix 


Simulation studies have been conducted to evaluate the effects of TDS attacks on the dynamics of the system and detect TDS attacks to direct the controller to emergency state. By solving the Riccati matrix equation we obtain the close loop control law in the form of state feedback. For the simulations we have used discrete linear-quadratic regulator design from continuous cost function called “lqrd” function in MATLAB 2013a. Table 1 shows parameter values used in this process. We also set both 

In our simulation, the total simulation time is 50 second and the sampling time is 0.01 s as its common in industrial applications. To show accuracy of our proposed TDS attack detector/tracker, we didn’t send negative acknowledgment to the local controller for the first simulation to only track the injected time delay to the system. The simulation has been done for three different scenarios: 1) single TDS attack on one power area, 2) Simultaneous TDS attack on both power areas, 3) Complex varied TDS attack on both power areas.
1) Single TDS attack to one power area: Here, we considered that adversary attacks the third state of the first power area at time of 2 second for a delay value of 3 seconds and the time delay is increased to 4.5 seconds at time of 7 seconds. Figure 2 shows that the detector accurately tracked and monitored the TDS attack or any
Table 1. Parameter values for a two-area power system controller design.
natural delay on the system.
2) Simultaneous TDS attack to both power areas: In this scenario, we attack the third state of both power areas. TDS attacks 1 and 2 have been injected to the first and the second power areas respectfully. TDS attack 1 is started at time 2 seconds for value 3 seconds and increased at time 8 seconds to the value of 4.5 seconds. Also TDS attack 2 is started simultaneously with TDS attack 1 for the value of 1.5 seconds and increased to the value of 6 seconds. Figure 3 shows the result.
3) Complex varied TDS attack to both power areas: In the last scenario we injected the TDS attack at different time with different time-delay values. We assume that an adversary injects TDS attack to feedback lines of both power areas. In our simulation, an attacker starts TDS attack to the second power area (third state) at time 1 second for 



For the second part of our simulation we enabled the emergency controller to show the effect of our proposed technique for overcoming the TDS attack. We assume that an adversary injects TDS attack to the feedback lines of both power areas. In the simulation, a TDS attack was applied to the second power area (the third state) at time of 1 second for 




Figure 2. TDS attack detection and tracking for third state of first power area.
Figure 3. TDS attack detection and tracking for simultaneous TDS attack on both power areas.
Figure 4. TDS attack detection and tracking for third state of first power area.
Figure 5. TDS attack detection and tracking for third state of second power area.
Figure 6. Value position of the turbine system under TDS attack for the first power-area control system.
Figure 7. Value position of the turbine system under TDS attack for the second power-area control system.
under attack with traditional optimal controller (TOC) and the proposed control technique (PCT) respectively. As it’s clear on the result, the simulated attack makes the system unstable. With the proposed technique, we could overcome TDS attack on the simulated system.
4. Conclusion
In summary, we have demonstrated a simple method for estimating and detecting time delay switch attack on a networked control system. The method relies on a time delay estimator that estimates and tracks time-delays introduced by an adversary. With knowledge of the maximum time delay of the control system, for which the plant remains stable and secure, the time-delay detector compares the estimated time delay to the maximum allowed time delay and issues an alarm signal when the estimated time delay is larger than this value. It also directs the system to an alarm state. In an alarm state, the plant is under the control of the emergency controller, which is local to the plant. The plant remains in this mode until the networked control system state is restored and time-delay switch is eliminated. We think that this method is simple and an inexpensive way to assure that an industrial control system remains stable and secure.
Acknowledgements
The authors would like to thank the Resilient, Autonomous Networked Control Systems (RANCS) group for support during publishing this paper.
Cite this paper
ArmanSargolzaei,Kang K.Yen,Mohamed N.Abdelghani,AbolfazlMehbodniya,SamanSargolzaei, (2015) A Novel Technique for Detection of Time Delay Switch Attack on Load Frequency Control. Intelligent Control and Automation,06,205-214. doi: 10.4236/ica.2015.64020
References
- 1. Ericsson, G.N. (2010) Cyber Security and Power System Communication—Essential Parts of a Smart Grid Infrastructure. IEEE Transactions on Power Delivery, 25, 1501-1507. http://dx.doi.org/10.1109/TPWRD.2010.2046654
- 2. Zhang, C.-K., Jiang, L., Wu, Q.H., He, Y. and Wu, M. (2013) Delay-Dependent Robust Load Frequency Control for Time Delay Power Systems. IEEE Transactions on Power Systems, 28, 2192-2201.
- 3. Yuan Y.L., Li Z.Y. and Ren, K. (2011) Modeling Load Redistribution Attacks in Power Systems. IEEE Transactions on Smart Grid, 2, 382-390.
- 4. Sargolzaei, A., Yen, K. and Abdelghani, M.N. (2014) Time-Delay Switch Attack on Load Frequency Control in Smart Grid. Journal of Advanced Communication Technologies, 5, 55-64.
- 5. Sargolzaei, A., Yen, K. and Abdelghani, M.N. (2014) Delayed Inputs Attack on Load Frequency Control in Smart Grid. Innovative Smart Grid Technologies Conference (ISGT), 2014 IEEE PES, Washington DC, 19-22 February 2014, 1-5. http://dx.doi.org/10.1109/isgt.2014.6816508
- 6. Sargolzaei, A., Yen, K.K. and Abdelghani, M.N. (2014) Control of Nonlinear Heartbeat Models under Time-Delay-Switched Feedback Using Emotional Learning Control. International Journal on Recent Trends in Engineering & Technology, 10, 2.
- 7. Amini, M.H., Sarwat, A.I., Iyengar, S.S. and Guvenc, I. (2014) Determination of the Minimum-Variance Unbiased Estimator for DC Power-Flow Estimation. 40th IEEE Industrial Electronics Conference (IECON 2014), Dallas, 29 October-1 November 2014, 114-118. http://dx.doi.org/10.1109/IECON.2014.7048486
- 8. Amini, M.H., Nabi, B. and Haghifam, M.-R. (2013) Load Management Using Multi-Agent Systems in Smart Distribution Network. IEEE PES General Meeting 2013, Vancouver, 21-25 July 2013, 1-5. http://dx.doi.org/10.1109/pesmg.2013.6672180
- 9. Kamyab, F., Amini, M. H., Sheykhha, S., Hasanpour, M. and Jalali, M.M. (2015) Demand Response Program in Smart Grid Using Supply Function Bidding Mechanism. IEEE Transactions on Smart Grid, 25 May 2015, 1949-3053. http://dx.doi.org/10.1109/TSG.2015.2430364
- 10. Li, Y., Tong, S.C. and Li, Y.M. (2012) Observer-Based Adaptive Fuzzy Backstepping Control for Strict-Feedback Stochastic Nonlinear Systems with Time Delays. International Journal of Innovative Computing, Information and Control, 8, 8103-8114.
- 11. Benzaouia, A., Ouladsine, M., Naamane, A. and Ananou, B. (2012) Fault Detection for Uncertain Delayed Switching Discrete-Time Systems. International Journal of Innovative Computing, Information and Control, 8, 8049-8062.
- 12. Sargolzaei, A., Yen, K., Noei, S. and Ramezanpour, H. (2013) Assessment of He’s Homotopy Perturbation Method for Optimal Control of Linear Time-Delay Systems. Applied Mathematical Sciences, 7, 349-361.
- 13. Benéitez-Péerez, H., Benéitez-Péerez, A. and Ortega-Arjona, J. (2012) Networked Control Systems Design Considering Scheduling Restrictions and Local Faults. International Journal of Innovative Computing, Information and Control, 8, 8515-8526.
- 14. Dotta, D., Silva, A.S. and Decker, I.C. (2009) Wide-Area Measurements-Based Two-Level Control Design Considering Signal Transmission Delay. IEEE Transactions on Power Systems, 24, 208-216. http://dx.doi.org/10.1109/TPWRS.2008.2004733
- 15. Kamwa, I., Grondin, R. and Hebert, Y. (2001) Wide-Area Measurement Based Stabilizing Control of Large Power Systems—A Decentralized/Hierarchical Approach. IEEE Transactions on Power Systems, 16, 136-153. http://dx.doi.org/10.1109/59.910791
- 16. Wu, H.X., Tsakalis, K.S. and Heydt, G.T. (2004) Evaluation of Time Delay Effects to Wide-Area Power System Stabilizer Design. IEEE Transactions on Power Systems, 19, 1935-1941. http://dx.doi.org/10.1109/TPWRS.2004.836272
- 17. Jiang, Q., Zou, Z. and Cao, Y. (2005) Wide-Area TCSC Controller Design in Consideration of Feedback Signals’ Time Delays. IEEE Power Engineering Society General Meeting, 2, 1676-1680.
- 18. Saad, M.S., Hassouneh, M.A., Abed, E.H. and Edris, A.A. (2005) Delaying Instability and Voltage Collapse in Power Systems Using SVCs with Washout filter-Aided Feedback. American Control Conference, 6, 4357-4362. http://dx.doi.org/10.1109/acc.2005.1470665
- 19. Chaudhuri, B., Majumder, R. and Pal, B. (2005) Wide-Area Measurement Based Stabilizing Control of Power System Considering Signal Transmission Delay. IEEE Power Engineering Society General Meeting, 2, 1447-1450. http://dx.doi.org/10.1109/pes.2005.1489106
- 20. Milano, F. and Anghel, M. (2012) Impact of Time Delays on Power System Stability. IEEE Transactions on Circuits and Systems I: Regular Papers, 59, 889-900. http://dx.doi.org/10.1109/TCSI.2011.2169744
- 21. Ray, S. and Venayagamoorthy, G.K. (2008) Real-Time Implementation of a Measurement-Based Adaptive Wide-Area Control System Considering Communication Delays. IET Generation, Transmission & Distribution, 2, 62-70. http://dx.doi.org/10.1049/iet-gtd:20070027
- 22. Alrifai, M.T., Zribi, M., Rayan, M. and Mahmoud, M.S. (2013) On the Control of Time Delay Power Systems. International Journal of Innovative Computing, Information and Control, 9, 769-792.
- 23. Yang, Q.Y., An, D. and Yu, W. (2013) On Time Desynchronization Attack against IEEE 1588 Protocol in Power Grid Systems. 2013 IEEE Energytech, Cleveland, 21-23 May 2013, 1-5.
- 24. Schenato, L. (2008) Optimal Estimation in Networked Control Systems Subject to Random Delay and Packet Drop. IEEE Transactions on Automatic Control, 53, 1311-1317. http://dx.doi.org/10.1109/TAC.2008.921012
- 25. Mahmoud, M.S. (2000) Robust Control and Filtering for Time-Delay Systems. Marcel Dekker Inc., New York.
- 26. Tan, Y.H. (2004) Time-Varying Time-Delay Estimation for Nonlinear Systems Using Neural Networks. International Journal of Applied Mathematics and Computer Science, 14, 63-68.
- 27. Li, C.M. and Xiao, J. (2006) Adaptive Delay Estimation and Control of Networked Control Systems. International Symposium on Communications and Information Technologies, 2006, ISCIT’06, Bangkok, 18-20 October 2006, 707-710. http://dx.doi.org/10.1109/iscit.2006.339832









