Intelligent Control and Automation
Vol. 4 No. 3 (2013) , Article ID: 35552 , 5 pages DOI:10.4236/ica.2013.43029
A Feedforward Controller to Regulate the Chemical Composition of Molten Steel in a Continuous Casting Tundish
Departamento de Materiales, Universidad Autonoma Metropolitana Azcapotzalco, Mexico City, Mexico
Email: bmma@correo.azc.uam.mx, dyolotzin@correo.azc.uam.mx, ihc@correo.azc.uam.mx
Copyright © 2013 Miguel A. Barron et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 1, 2013; revised July 1, 2013; accepted July 8, 2013
Keywords: Chemical Composition; Continuous Casting; Distributed Parameter System; Feedforward Controller; Molten Steel; Tundish
ABSTRACT
A feedforward controller for the automatic regulation of chemical composition of molten steel in the tundish of a continuous casting machine is proposed in this work. The flow of molten steel inside the tundish is modeled as a distributed parameter system, and the resulting partial differential equation is transformed into a set of ordinary differential equations by means of the finite differences technique. From the above set and using a proper boundary condition, a feedforward control law is synthesized. No experimental tests are reported, however, the dynamic performance of the controller is illustrated by means of numerical simulations.
1. Introduction
Nowadays, the demand for steels with tighter chemical compositional ranges has increased dramatically. This has forced steel producers to improve plant efficiency through the development and installation of advanced control systems. Traditionally, the final composition adjustment is carried out in the ladle in which the molten steel is poured from the furnace. Unfortunately, with the above procedure the percentage of heats out of specification is frequently unacceptable given that the oxygen content of the steel bath decreases the content of those easily oxidizable elements, such as silicon, manganese and chromium. A proposal to carry out the final compositional trimming in the continuous casting tundish is made in [1]. Here, the steel outlet composition is determined by an in-situ continuous laser analyzer, then a proportional-integral-derivative controller compares the outlet composition with a manually-input set point and determines the speed of an alloy-wire feeding equipment.
In the literature, the modeling and control of distributed parameter systems (DPS) have been addressed before [2-4]. Sometimes, partial differential equations (PDE) are transformed into a set of ordinary differential equations (ODE) using some kind of technique such as orthogonal collocation [5-7] or the method of characteristics [8-10]. On the other hand, synthesizing of feedback linearizing control laws from low-order, lumped-parameter models, are reported in [11]. In this work a modelbased control scheme for the automatic regulation of the steel chemical composition in the continuous casting tundish by means of feeding a wire-alloy is proposed (Figure 1). The steel flow is considered as a plug flow one, and therefore it is modeled as a DPS with time and tundish length as independent variables. The resulting PDE is converted into a set of ODE by the finite differences technique, then a feedforward control law to calculate the alloy-wire feeding speed is derived. The dynamic performance of the controller is tested by means of numerical simulations.
2. Mathematical Modelling
Assuming a plug flow of the molten steel in the tundish, the partial differential equation which governs the mass transport of element A is given by [12]:
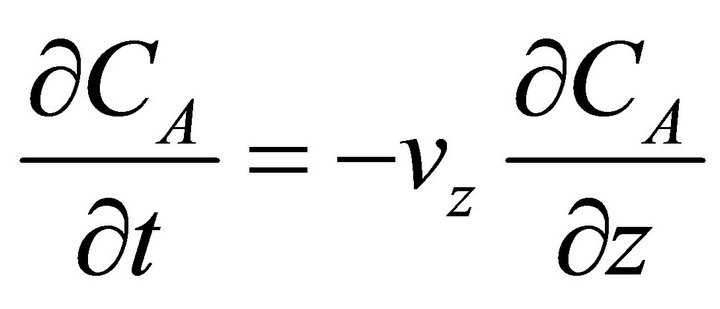 (1)
(1)
where CA is the concentration of element A, t is the time,

Figure 1. The proposed feedforward controller.
vz is the mean velocity of the molten steel in the tundish, and z is the tundish length coordinate. The above equation implies that: 1) the density of the molten steel is constant; 2) there is no diffusivity of A; and 3) the axial component of the velocity is the only significant one. The initial condition is given by:
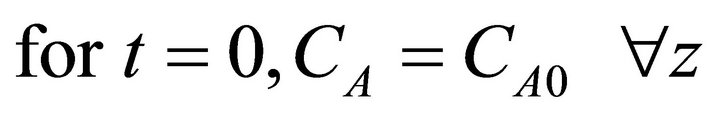 (2)
(2)
which means that initially the whole volume of steel in the tundish has a concentration of element A equal to CA0. The boundary condition is determined from the mass contributions of the inlet steel flow (CA0) and the alloywire feed (CAw) as follows:
 (3)
(3)
where
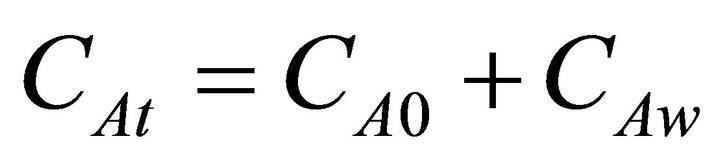 (4)
(4)
and
 (5)
(5)
In the above equations CAt is the concentration of A in the first slice of the tundish, vw is the alloy-wire feeding speed, Aw is the cross sectional area of the alloy wire, rw is the wire density, fAw is the mass fraction of A in the alloy wire, MA is the atomic weight of A, and Qi is the volumetric flow rate of the incoming molten steel.
3. Feedforward Controller: Synthesis and Asymptotic Stability
In order to regulate the concentration of the element A at the tundish exit, the alloy-wire feeding speed is chosen as the control input. The need for a feedforward controller arises from the fact that the effects of the delay in the control action due to the distributed nature of the system must be minimized, so the controller must act beforehand in an anticipatory manner to reject disturbances [13]. Besides, given the absence of chemical reactions, stabilizing the inlet concentration implies the stabilization of the outlet concentration.
In order to get an adequate control law, the partial differential equation given by Equation (1) is transformed into a finite set of coupled ordinary differential equations by means of the backwards finite differences technique [14]:
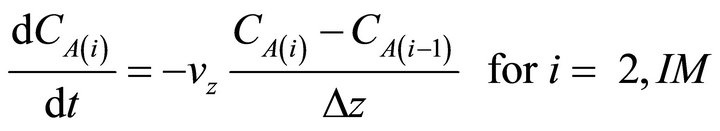 (6)
(6)
where CA(i) is the concentration of A at node i, Dz is the length step and IM is the amount of ODE. The length step is determined in this way:
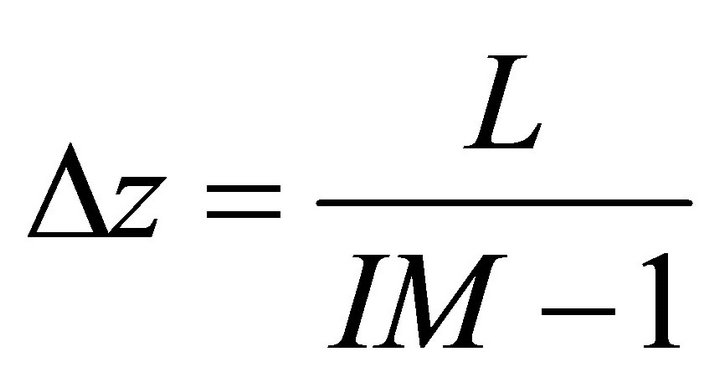 (7)
(7)
where L is tundish length.
Employing a forward finite difference scheme for z = 0 (i.e. i = 1), and considering the boundary condition given by Equation (3) and Equation (5), the following expression is obtained:
 (8)
(8)
In this work, regulation of the outlet concentration is achieved by stabilizing the inlet concentration. This is possible by assuming a lack of chemical reactions inside the tundish. Assuming that CA(1) has an asymptotically stable behavior, the following expression holds:
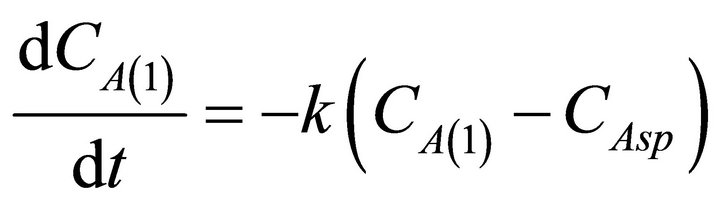 (9)
(9)
then, it is verified that
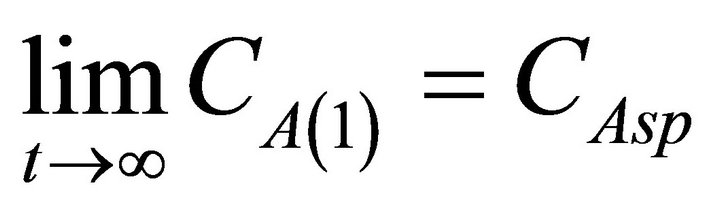 (10)
(10)
where CAsp is the concentration set point. Substituting Equation (9) into Equation (8) yields
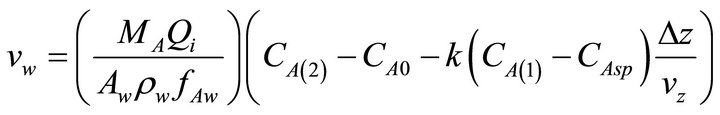 (11)
(11)
Equation (11) can not be employed as control law given that CA(2) is unknown. If Dz is small, then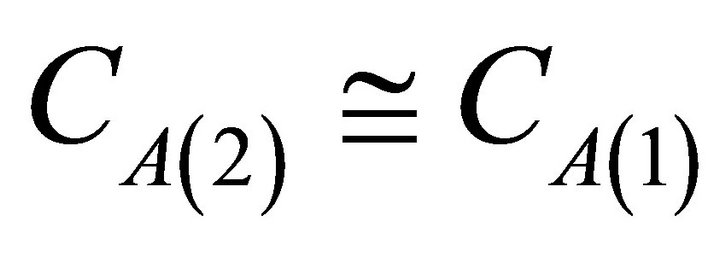 . This is achieved if MI (i.e. the amount of ODE) is large enough. Then, considering the boundary condition of Equation (3), the following feedforward control law is finally obtained:
. This is achieved if MI (i.e. the amount of ODE) is large enough. Then, considering the boundary condition of Equation (3), the following feedforward control law is finally obtained:
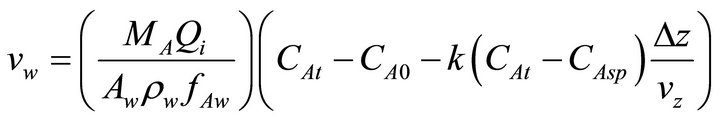 (12)
(12)
Besides, given that the value of Dz can be set in an arbitrary way, if Dz ® 0 (or IM ® ¥), then, in accordance with Equation (11), the control input becomes independent from the control gain:
 (13)
(13)
At steady state CAt = CAsp, therefore the value of the control input associated to the concentration set point is given by:
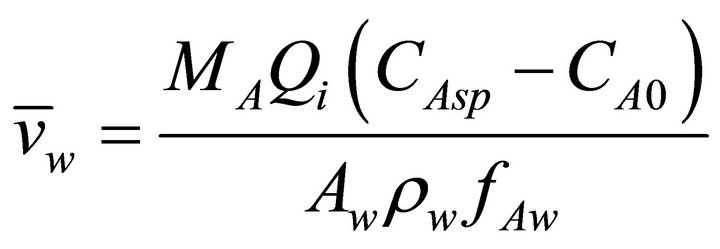 (14)
(14)
4. Numerical Simulations: Results and Discussion
Numerical simulations were carried out in order to test the performance of the controller. An amount of 101 ODE was considered in order to reduce the size of the length step and ensure a right closed-loop behavior of the system. In Table 1 are shown the system parameters. The control objective was to stabilize the outlet concentration of element manganese at CAsp = 0.10 kgmol∙m−3. The manganese concentration in the inlet steel flow from the ladle is assumed CA0 = 0.05 kgmol∙m−3. Figure 2 shows the evolution of the outlet manganese concentration for a value of the control gain k = 1.0 min−1. The response of the control action is delayed until the time elapsed is near

Table 1. Parameter values.
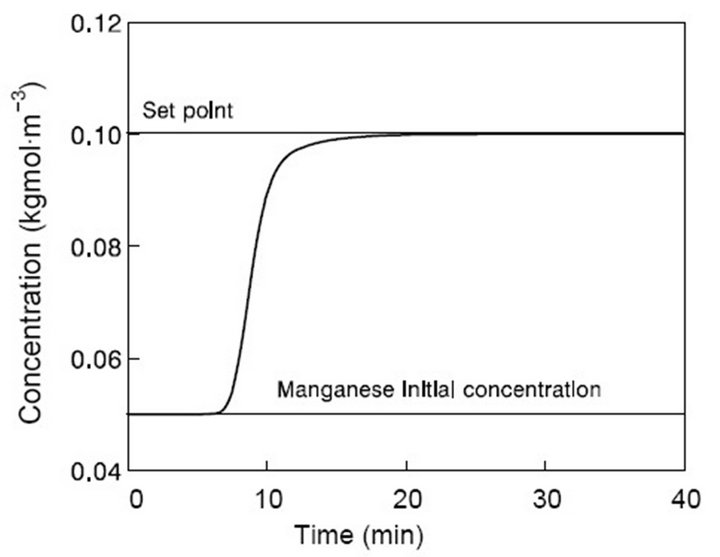
Figure 2. Evolution of outlet manganese concentration.
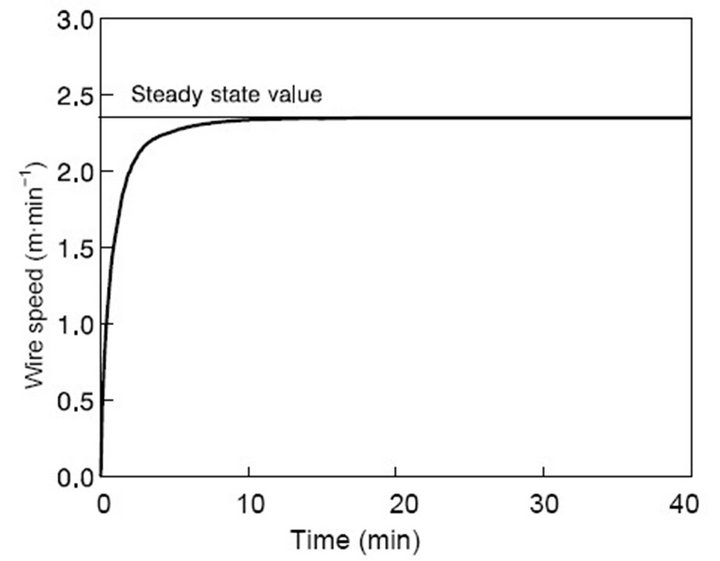
the mean residence time of the tundish (8.18 min). When a time around 14 min has elapsed, the asymptotic convergence to set point of the manganese concentration is achieved. The corresponding evolution of the control input is shown in Figure 3. The wire feeding speed quickly reaches its steady state value of 2.35 m∙min−1, which is given by Equation (14).
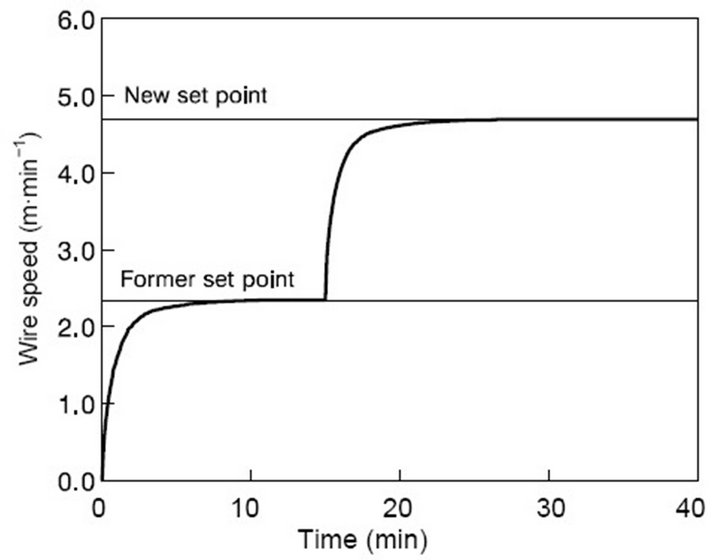
The response of the controller to set point changes is illustrated in Figure 4. The set point changes from 0.10 to 0.15 kgmol∙m−3 when 15 min from start time has elapsed. Manganese concentration continues at the former set point during a period of time similar to the mean residence time, then it decreases until it reaches the new set point. The evolution of the corresponding wire feeding speed is shown in Figure 5. Given that the new set point is above the former one, the controller responds increasing the wire feeding speed from 2.35 to 4.69 m∙min−1.
The response of the controller to disturbances in the incoming volumetric flow can be seen in Figure 6. The flow suffers a sudden change from 0.2347 to 0.1174

Figure 4. Dynamic performance of the controller for a change in set point.
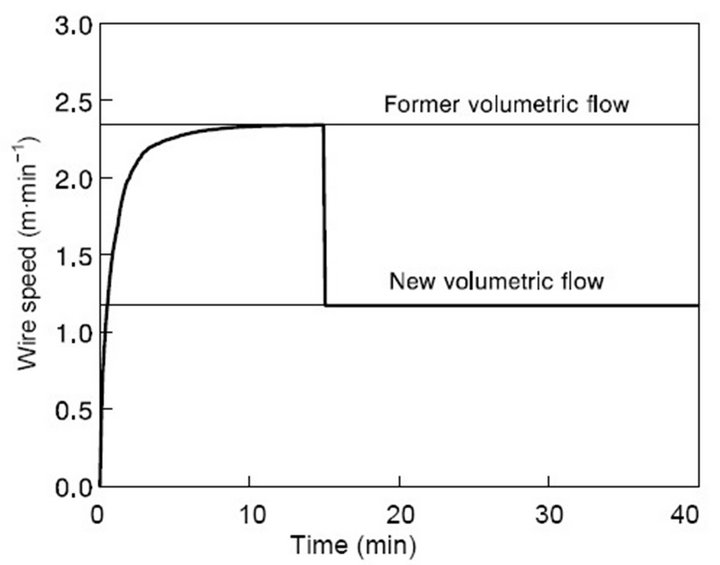
Figure 6. Behavior of the wire feeding speed for a disturbance in volumetric flow.
m3∙min−1 when 15 min from start has elapsed. To take into account the decrease in the volumetric flow of steel, the controller reduces the feeding speed of the alloy-wire from 2.35 to 1.17 m∙min−1.
5. Conclusions
Molten steel flow inside a continuous casting tundish was modeled as a distributed parameter system. Computer runs showed that transforming the resulting partial differential equation into a set of ordinary differential equations by means of finite differences is a right technique to synthesize a feedforward controller in order to regulate automatically the chemical composition of molten steel. Numerical simulations, which corroborate the asymptotic stability of manganese outlet concentration, show a proper dynamic performance of the feedforward controller, particularly for changes in the set point and inlet volumetric flow.
Future work must consider the implementation and evaluation of the dynamic performance of the proposed controller in actual tundishes or water models.
REFERENCES
- R. Widdowson, “Development of Compositional Trimming and Control in the Concast Tundish Based on in Situ Liquid Steel Analysis,” Report EUR 18300 EN, European Commission, 1998.
- M. A. Demetriou, “Synchronization and Consensus Controllers for a Class of Parabolic Distributed Parameter Systems,” Systems & Control Letters, Vol. 62, No. 1, 2013, pp. 70-76. doi:10.1016/j.sysconle.2012.10.010
- M. R. Garcia, C. Vilas, L. O. Santos and A. A. Alonso, “A Robust Multi-Model Predictive Controller for Distributed Parameter Systems,” Journal of Process Control, Vol. 22, No. 1, 2012, pp. 60-71. doi:10.1016/j.jprocont.2011.10.008
- E. Aguilar-Garnica, J. P. Garcia-Sandoval and P. Gonzalez-Alvarez, “PI Controller Design for a Class of Distributed Parameter Systems,” Chemical Engineering Science, Vol. 66, No. 18, 2011, pp. 4009-4019. doi:10.1016/j.ces.2011.05.025
- D. Bonvin, R. G. Rinker and D. A. Mellichamp, “On Controlling an Autothermal Fixed-Bed Reactor at an Unstable Steady State,” Chemical Engineering Science, Vol. 38, No. 2, 1983, pp. 233-244. doi:10.1016/0009-2509(83)85005-2
- H. M. Budman, C. Webb, T. R. Holcomb and M. Morari, “Robust Inferential Control for a Packed-Bed Reactor,” Industrial Engineering & Chemistry Research, Vol. 31, No. 7, 1992, pp. 1665-1679.
- A. Cinar, “Controller Design for a Tubular Catalytic Reactor,” Canadian Journal of Chemical Engineering, Vol. 62, No. 6, 1984, pp. 746-754. doi:10.1002/cjce.5450620604
- E. M. Hanczyc and A. Palazoglu, “Sliding Mode Control of Nonlinear Distributed Parameter Chemical Processes,” Industrial Engineering & Chemistry Research, Vol. 34, No. 2, 1995, pp. 557-566.
- E. M. Hanczyc and A. Palazoglu, “Nonlinear Control of a Distributed Parameter Process: The Case of Multiple Characteristics,” Industrial Engineering & Chemistry Research, Vol. 34, No. 12, 1995, pp. 4406-4412. doi:10.1021/ie00039a032
- H. Sira-Ramírez, “Distributed Sliding Mode Control in Systems Described by Quasilinear Partial Differential Equations,” Systems & Control Letters, Vol. 13, No. 2, 1989, pp. 177-181. doi:10.1016/0167-6911(89)90036-4
- F. J. Doyle III, H. M. Budman and M. Morari, “Linearizing Controller Design for a Packed-Bed Reactor Using a Low-Order Wave Propagation Model,” Industrial Engineering & Chemistry Research, Vol. 35, No. 10, 1996, pp. 3567-3579. doi:10.1021/ie9404083
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, “Transport Phenomena,” 2nd Edition, John Wiley & Sons, New York, 2007.
- G. Stephanopoulos, “Chemical Process Control,” PrenticeHall, Englewood Cliffs, 1984.
- S. Chapra and R. Canale, “Numerical Methods for Engineers,” 6th Edition, McGraw Hill College, Columbus, 2009.
Nomenclature
Aw: cross sectional area of the alloy wire, m2
At: cross sectional area of the tundish, m2
CA: concentration of the element A, kgmol∙m−3
CAt: concentration of A in the first slice of the tundish, kgmol∙m−3
CA0: concentration of A in the incoming steel flow, kgmol∙m−3
CAsp: set point concentration, kgmol∙m−3
fAw: weight fraction of A in the alloy wire, dimensionless IM: amount of ordinary differential equations k: control gain, min−1
L: tundish length, m MA: atomic weight of A, kgmol∙kg−1
Qi: volumetric flow rate of the incoming steel, m3∙min−1
t: time, min vw: alloy wire feeding speed, m∙min−1
vz: mean velocity of the molten steel in the tundish, m∙min−1
z: tundish length coordinate, m rw: alloy wire density, kg∙m−3