ABSTRACT

In this paper, we discuss questions of creating an electronic intellectual analogue of a human being. We introduce a mathematical concept of stimulus generating emotions. We also introduce a definition of logical thinking of robots and a notion of efficiency coefficient to describe their efficiency of rote (mechanical) memorizing. The paper proves theorems describing properties of permanent conflicts between logical and emotional thinking of robots with a nonabsolute rote memory.

1. Introduction

First, it should be noted that the rote or mechanical memory in this paper is the ability of a robot or human to memorize some certain data in every detail but without regard to the meaning content of that information. Modern computers have exactly this kind of memory: they can store in memory a complete collection of symbols without picking and separating the meaning content of a text out of that set of symbols; and, besides, they never “forget” anything. So, modern computers possess an absolute mechanical memory.

As opposed to modern computer systems, in the present paper we consider computers which can forget older information. A good example of a computer with a nonabsolute memory is an infected computer when a virus attack destroys a part of data on a hard disk. Below we investigate only mathematical properties of computersrobots with a mechanical (rote) memory.

In article some aspects of the general mathematical theory of emotions of robots regardless of type of these emotions are considered.

Currently researchers in the USA try to solve a problem of creating an electronic copy (analogue) of human being called an E-creature [1].

Let us try to study this overseas idea in terms of information.

First it should be noted that there is no human being possessing an absolute memory, i.e. he or she always forgets a part of acquired information as this is his\her nature.

Now let us introduce a couple of definitions.

Definition 1. A portion is a quantity (amount) of new data memorized by a human being completely.

Definition 2. A data time step (or an information time step) is an arrival time of a portion into chips of an E-creature.

Before we start, let us note one obvious property of the portion: a number of bits in the portion i is limited i.e. there is such s for which the inequalities

are always valid.

Let us introduce a formula

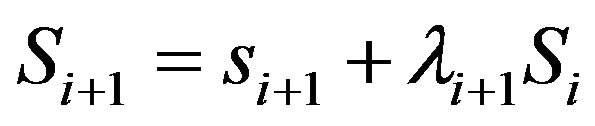, (1)

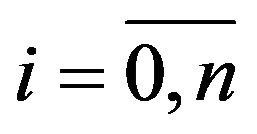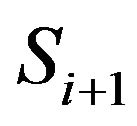where i is the number of the information time step,; is the ^st portion, is the total quantity of information memorized by a human through i + 1 information time steps, is the information memory coefficient which characterizes a part of total memorized information received during previous i data time steps.

Assume that the information memory coefficient corresponding to the end of the data time step satisfies the following conditions:

, (2)

,.

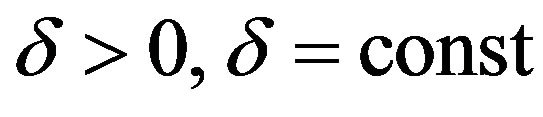By virtue of the information property, 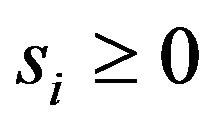holds true, consequently all the accumulated information is greater than or equal to zero.

Suppose we have created an electronic analogue of a human. Let us prove one of the information properties of this analogue.

Theorem 1. Under (2) the total amount of information S which can be memorized by the chip of the analogue is limited.

Proof. From (1) and (2) we can easily obtain the following inequality:

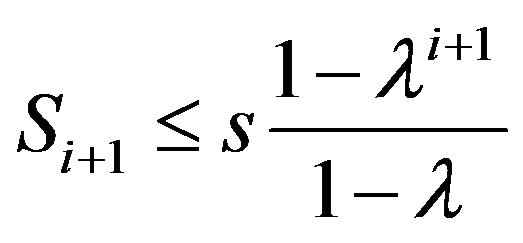. (3)

Proceeding to the limit in InEquation (3) with an infinite increase of time steps (time of existence of an immortal human being) we obtain the chain of relations

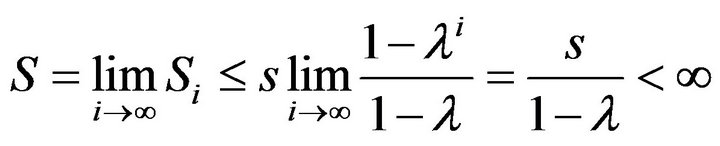
Thus, the theorem is proved.

Corollary. It is impossible to create an E-creature with a nonabsolute memory which would be able to accumulate information infinitely.

Its proof is evident from the formulation of Theorem 1.

So, if we can prove that the human rote memory satisfies Conditions (2), we will be able to conclude that it is impossible to create the only infinitely existing E-creature which would be an evolving analogue of a human being (at least, in terms of information).

An immortal (infinite) electronic creature able to accumulate information infinitely [1] is possible in case if, for instance, it has an absolute information storage (information memory) with the conditions 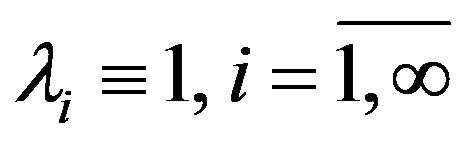satisfied; but that creature would have nothing to do with a human being analogue, forgetful and oblivious; that sort of creature could be called just a robot with an absolute memory.

As for the infinite information evolution of the Ecreature with a nonabsolute memory we can state that it is necessary that the information from a chip of the “ancestor” E-creature with the nonabsolute memory should be downloaded to a chip of the “successor” E-creature (with the nonabsolute memory as well) right when the amount of the accumulated information becomes close to S. For the purpose of further data accumulation by the E-creature (which is a copy of a human being with a nonabsolute memory) it is necessary to re-download all the information from the ancestor’s chip to the chip of the successor on a regular basis, i.e. is supposed to be equal to where k is the number of data (information) time steps performed by the ancestor E-creature in the full course of its existence.

Let us note one property of information memory coefficients varying during the data time step length t with.

Theorem 2..

Proof. let us write down the formula analogous to (1):

. (4)

But at the initial moment of the information time step the relations

(5)

hold true.

Substituting (5) into Relation (4) and solving the obtained equation relative to we get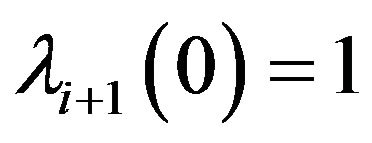, which was to be proved.

Let us define a linear dependence enabling us to describe approximately the change in the information memory coefficient during the information time step.

Obviously,. Consequently,

. (6)

holds true.

Suppose that 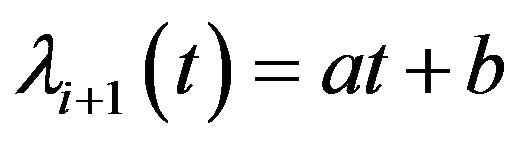is correct.

By Theorem 2 and Formula (6) the system of linear equations

, (7)

(8)

is correct.

Solving this system of Equations (7) and (8) we have

.

Thus we can write down the following formula

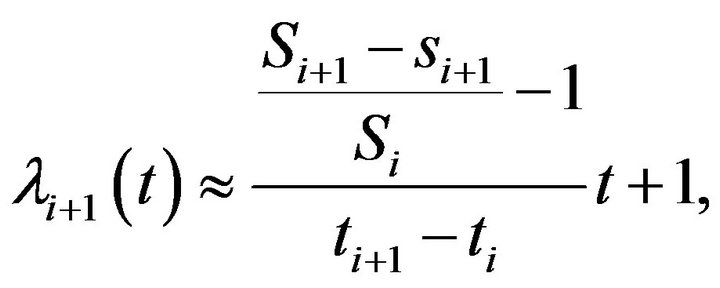
with.

Now let us introduce a couple more definitions.

Definition 3. The function 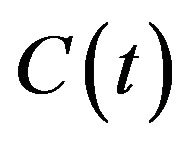is referred as a stimulus if it has the following properties:

1) The function domain of C(t):;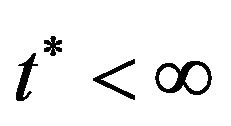

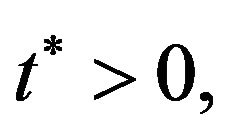
2) C(t) > 0 for any;

3) C(t) is the single-valued continuous function;

4) C(t) is the bounded function.

Definition 4. The function S(t) is referred as a subject if it has the following properties:

1) the function domain of S(t):;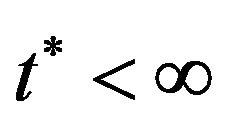

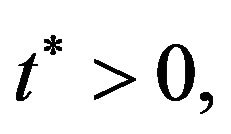
2) S(t) > 0 for any;

3) S(t) is the biunique (one-to-one) function;

4) S(t) is the bounded function.

The following theorem based on the definitions given above is obvious.

Theorem 3. The function 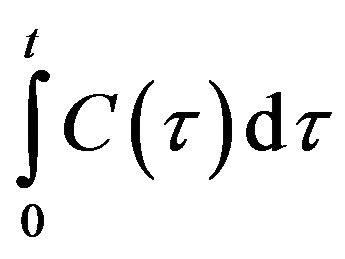is the subject where.

The proof is obvious.

We assume that the relation where

is the stimulus with the domain holds true.

It is easy to prove the following theorem.

Theorem 4. If 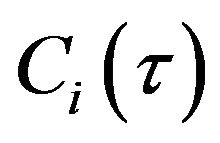is the data transmission rate then is the numerical value of the subject corresponding to the end of the -th information time step.

The proof is obvious.

Definition 5. A logical action of a robot is a process which can be described by an algorithm.

Definition 6. An informational robot is a robot featuring logical actions.

Definition 7. If a process of data memorizing by a robot is described by information memory coefficients satisfying Conditions (2) this robot can be called a robot with a nonabsolute memory (nonabsolute-memory robot).

Assume that our robot has to make a logic decision as a result of the subject effect. Let us introduce a hypothesis that the robot estimates a logic result of its intellectual action on the basis of a sign and a value of the informational education 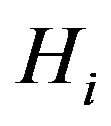generated in its chips by the obtained logic action.

Without loss of generality, we can write down the following relation:

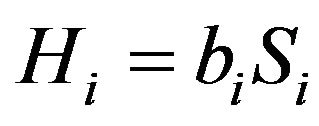with.

Now let us introduce one more hypothesis: the coefficient specifies the sign of an emotional result entailing the education as a result of the robot’s logic action.

Theorem 5. If the sequence of coefficients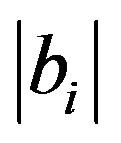, is uniformly bounded and Relations (2) are valid, then the inequalities

,

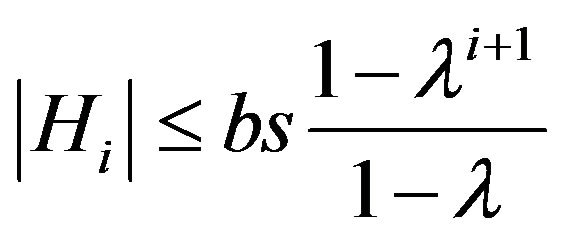with 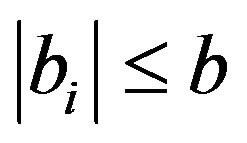also hold true.

Proof. The validity of 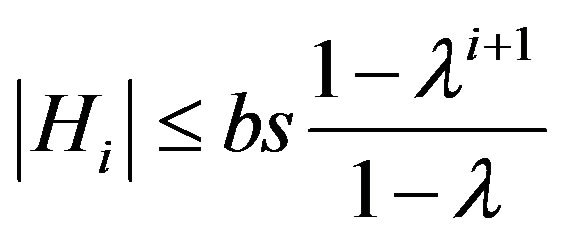obviously follows from (3). The validity of the second inequality follows from the chain of relations

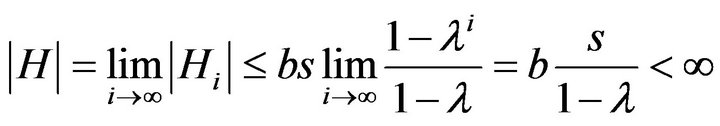which establishes the theorem.

Corollary. Under the hypothesis of Theorem 5 informational educations corresponding to the ends of information time steps are bounded and tend to a constant value under the infinite increase of lifetime of the robot with a nonabsolute memory.

The proof is obvious.

The result of logical thinking of the robot is expressed also in the form of emotions which are defined by the coefficients set by developers of robotic system depending on.

Definition 8. The function f(t), satisfying the relation (where a(s(t),t) is the arbitrary function) is the function of robot’s inner emotional experience.

Let us state that the subject S(t) initiates the robot’s inner emotional experience.

Definition 9. A robot’s inner emotional experience function M(t) is called an emotion if it satisfies the following conditions:

1) The function domain of M(t):;

2) 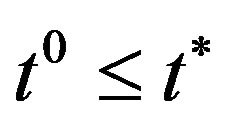(note that this condition is equivalent to emotion termination in case the subject effect is either over or not over yet);

3) M(t) is the single-valued function;

4);

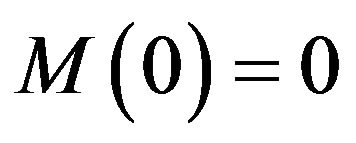5);

6) M(t) is the constant-sign function;

7) There is the derivative 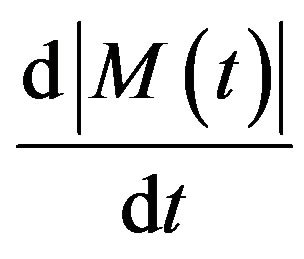within the function domain;

8) There is the only point z within the function domain, such that 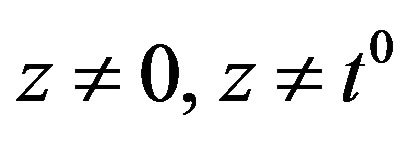and;

9) 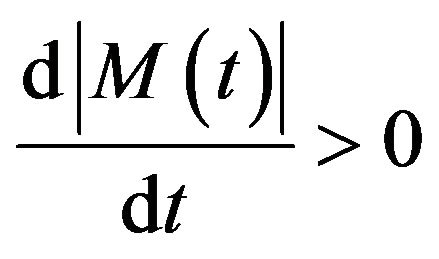with;

10) 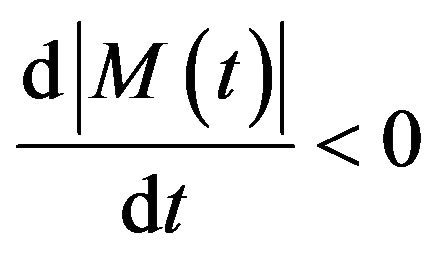with.

Let us assume there is such J > 0 that for any emotions of the robot the condition is valid.

Let us introduce the definition of emotional upbringing (emotional education) of a robot [2] abstracting from the psychological matter of the concept of education/upbringing.

Definition 10. An upbringing or education of a robot is a relatively stable attitude of this robot towards a subject (stimulus).

From Definition 9 it follows that the robot’s emotion M(t) is the continuous function on the segment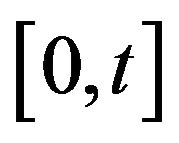, consequently, M(t) is integrable on this segment. Considering that, we can work out the following definition.

Definition 11. The robot’s elementary education r(t) based on subjects S(t) is the following function:

(9)

In virtue of Definition 11, provided that Integrand Function (9) is the emotion, the function r(t) is differentiable with respect to the parameter t, so the relation 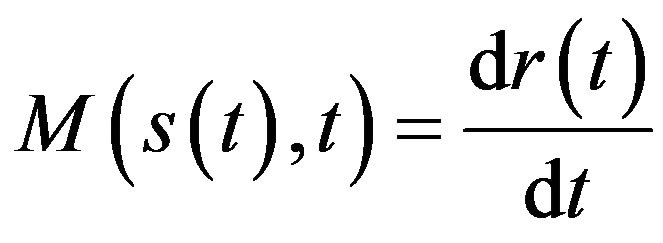is valid.

Let us assume that in the course of time a robot can forget emotions experienced some time ago. Its current education is less and less effected by those older (bygone) emotions. Consequently, its older elementary educations initiated in the past by those emotions become forgotten as well.

Hence, the following definition becomes obvious.

Definition 12. The education R(t) of a robot based on the subjects S(t) is the following function:

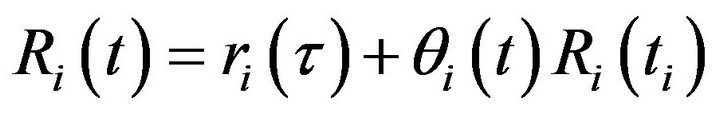, (10)

where t is the current time,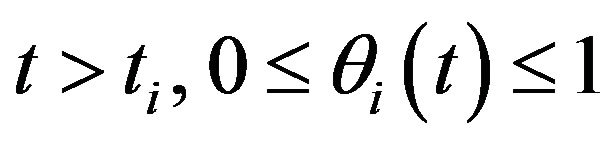. The current time satisfies the relation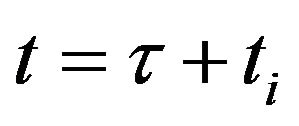, where is the current time of the current emotion effect from the very beginning of its effect, is the total effect time of all the formerly experienced (older) emotions, is the education obtained by the robot within the period of time.

A verbal definition of education is as follows: it is a value determining the stability of the robot’s behavior motivation based on a certain set of subjects.

Definition 13. Coefficients are the memory coefficients of older events (experienced in the past), i.e. coefficients of the robot’s memory.

According to (10) we can write down a relation specifying the education in the beginning of the i + 1^st emotion effect upon the robot:

.

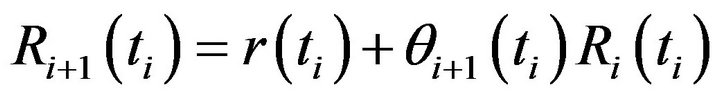It is easy to see that the eqs.

hold true.

Consequently 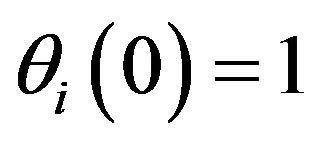is valid.

Definition 14. A time step is an effect time of one emotion.

According to results obtained in psychological researches an emotion cannot last more than 10 seconds. Therefore, let us assume that a time step value of any robot emotion is less or equal to 10 sec.

Hereinafter psychological characteristics of robots corresponding to the current time step are bracketed after the variable, and psychological characteristics corresponding to the ends of time steps are denoted without brackets. For instance, defines a function of education altering for the current time t of the current time step i, and 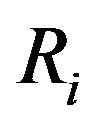defines a value of education in the end of the time step i.

It is easy to see that the robot featuring the older event memory coefficient identical with 1 remembers in detail all its past emotional educations. This robot can be regarded as autistic. But let us suppose that the robot’s memories of the older events are deleted, i.e. the twosided inequality is valid for the forgetful robot at the end of each time step. We are now in position to state a theorem for this kind of robot.

It is easy to see that Relation (10) is equivalent to

. (11)

Equation (11) can take the form

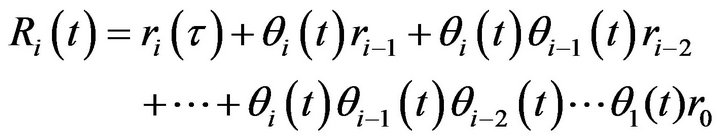(12)

Definition 15. Emotions initiating equal elementary educations at the end of the time step are tantamount.

Definition 16. A uniformly forgetful robot is a forgetful robot whose memory coefficients corresponding to the end points of each emotion effect time are constant and equal to each other.

It is obvious that the education of the uniformly forgetful robot with tantamount emotions can be found by the formula

with:, , the time step order number.

Let us consider the case when the decision obtained in the course of intellectual activity of the robot causes both the emotional education [2] and informational education which is a result of logical action assessment.

In this case we can speak about a stupor (a state of psychological conflict between emotions and logics of a robot) [2], causing the following equality:

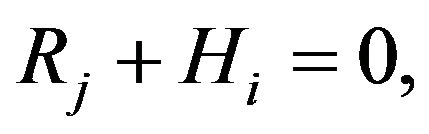(13)

where j is the order number of the emotion time step [2].

Assume that the validity of implies the emotion-based decision of the robot and the validity of 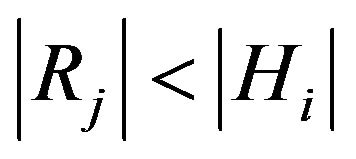implies the logic-based decision.

Now let us introduce several more definitions.

Definition 17. A dummy information time step is an interval equal to the information time step but without any information effect upon the robot.

Definition 18. A uniformly-informational robot is an informational robot with equal portions for any of information time steps.

Definition 19. A tantamountly-forgetful robot is an informational robot with a nonabsolute memory with all its information memory coefficients equal to each other.

We are now in a position to state a theorem for those kinds of robots.

Theorem 6. For a uniformly forgetful robot with tantamount emotions [2] (which is both uniformly-informational and tantamountly-forgetful) the condition of stupor caused by the alternate selection between logical and emotional decisions is defined by the relation

with: j the order number of the emotion time step, i the order number of the information time step,.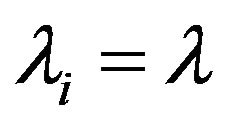

The proof follows from Condition (13), the formula of the education of uniformly forgetful robots with tantamount emotions and the hypotheses of Theorem 6.

It should be noted that according to the theorem of anti-stupor coefficients given in [2], if is valid, there exists the coefficients and for which the condition of stupor will never ensue under any j and i.

An example of such coefficients is 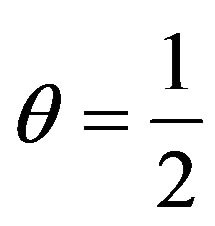and.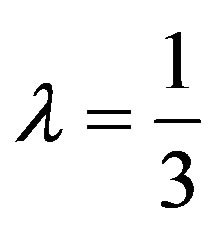

Obviously, when holds, the robot makes an alternate decision in favor of emotions, but when 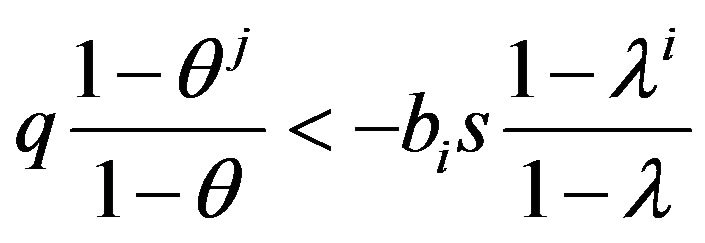holds, the decision is made in favor of logics.

Let us consider the conflict between the uniformly forgetful robot with tantamount emotions and the absolute-memory robot with tantamount emotions.

It is obvious that the condition of that kind of conflict between those two robots has the form:

. (14)

Assume q = –z is valid, then Relation (14) is equivalent to

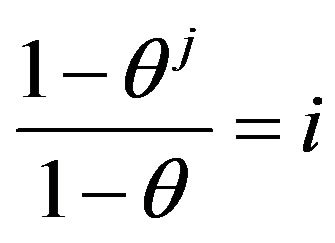. (15)

Let us state and prove the following theorems:

Theorem 7. The conflict between the uniformly forgetful robot with tantamount emotions q and the absolute-memory robot with tantamount emotions –q is possible at the first time step of the education process.

Proof. Obviously, if the equalities 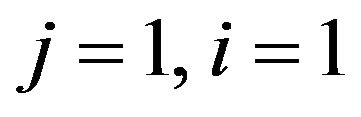are valid, Relation (15) reduces to the identity which proves the theorem.

Theorem 8. There are anti-conflict memory coefficients under which the conflict between the uniformly forgetful robot with tantamount emotions and elementary educations q and the absolute-memory robot with tantamount emotions and elementary educations –q is not possible in case is valid.

Proof. Let us show that under the hypothesis of Theorem 8 there exists the memory coefficient for which Relation (15) never gets reduced to an identity.

Obviously, Relation (15) is equivalent to the formula

. (16)

Assume that the relation holds true. Substituting the latter into Equation (16) we obtain the following equation:

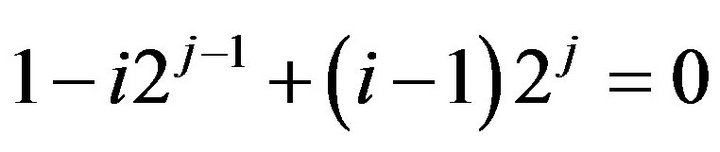, (17)

from which it follows that

. (18)

For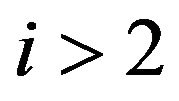, the right-hand member of (18) is negative, and left-hand is positive. It means that Identity

(15) is not possible with.

Let us consider Equation (17) under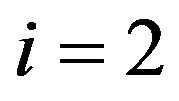. Obviously, in this case (17) has the form of the incorrect numerical identity.

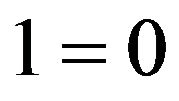So, 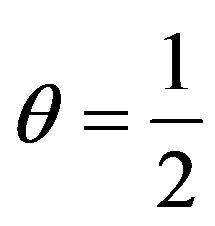is definitely the anti-conflict coefficient.

The theorem is proved.

It is quite easy to see that 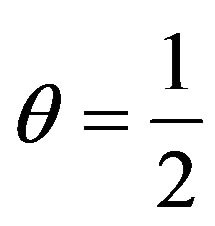becomes the antistupor memory coefficient [2] in case of uncertainty (or co-called ambiguity) of the alternate selection [2] between forgettable tantamount emotions and not forgettable tantamount emotions.

If 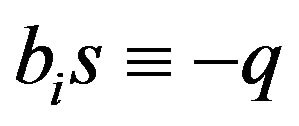is valid, the conflict between the emotional and logical constituents of mental process results of the uniformly-informational uniformly forgetful robot with the absolute logical memory never occurs (with more than 1 information time step) for the memory coefficient satisfying the equality.

Analogously, we can lay down the following: when 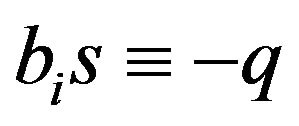is valid, the conflict between the emotional and logical constituents of mental process results of the uniformly-informational uniformly forgetful robot with the absolute emotional memory never occurs (with more than 1 information time step) for the memory coefficient satisfying the equality.

On this basis we can assert that we found the universal anti-stupor and anti-conflict memory coefficient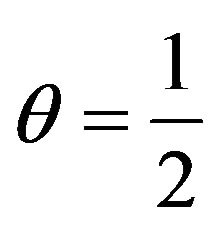

allowing the robot without either logical or emotional absolute memory to avoid stupors and conflicts.

Definition 20. An eternal conflict is a permanent conflict under any i and j.

Obviously, the permanent conflict for forgetful robots with tantamount and uniformly-informational characteristics can be described by the relation

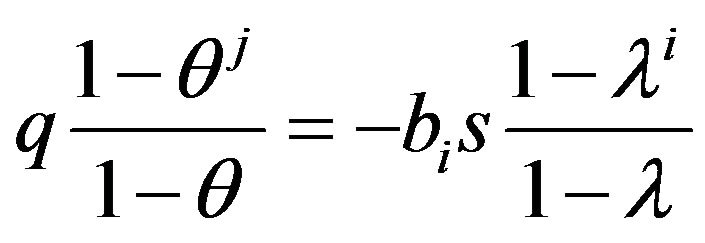
which is equivalent to the relation

. (19)

Let us hold i fixed and introduce the following designation:.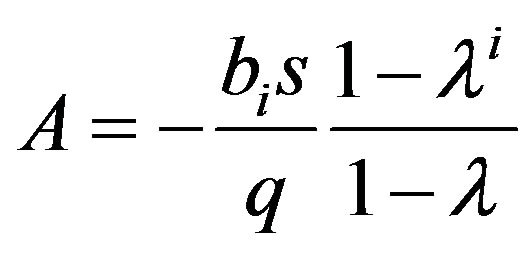

Equation (19) will have the form

. (20)

It is easy to see that (20) implies the relation

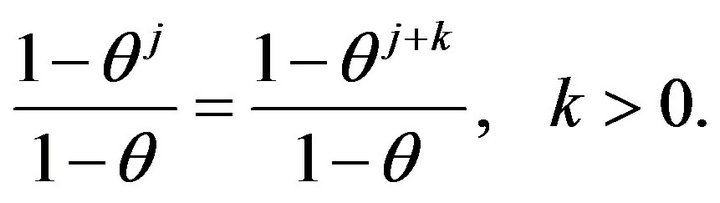(21)

The solution of Equation (21) is.

So, Equation (21) is equivalent to the relation

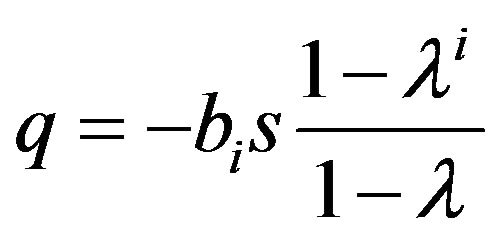at that 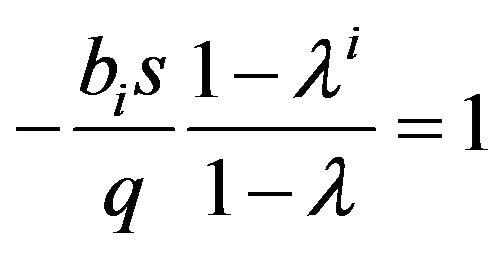is vslid.

Consequently, the necessary condition of eternal conflict is the validity of

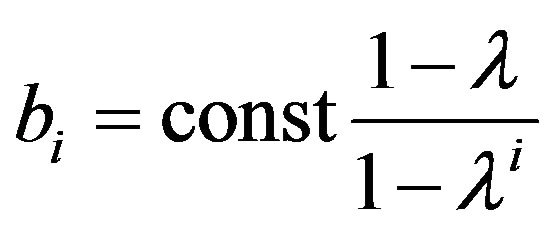. (22)

Let us consider the case when one of the robots has an absolute information memory.

By analogy with the previous mathematical manipulations we can show that in this case the condition of the eternal conflict is the validity of.

So, the necessary condition of the eternal conflict takes the form

. (23)

We can set the values 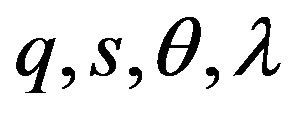and dependencies 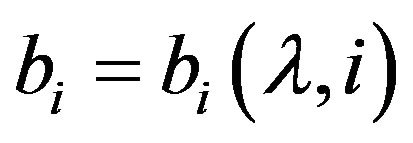for our robots so that to model their behavior while they make alternate decisions.

Note that in the case of eternal conflict the robot remains in the state of undecidable selection while making an alternate decision in favor of emotional or informational education. This makes the robot “feel” vacillating and ambiguous about its action initiated by the alternate selection.

For implementation of rules of Ayzik Azimov, in our opinion, it is necessary to be guided by rules of an emotional choice of the robot which are described in works: [2-5].

Let us study the properties of information accumulateing by the robot.

Obviously, the information already stored in the memory of the robot with the nonabsolute informational memory in the absence of new information satisfies the inequalities

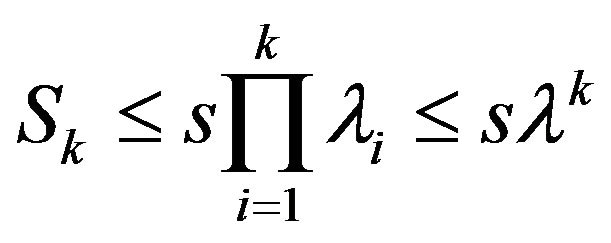where k is the number of dummy information time steps characterizing the time of forgetting data by the robot.

Definition 21. A complete information cycle is a number of information time steps equal to a number of time steps under the effect of new information plus a number of time steps in the absence of new information.

So, the information accumulated and stored by the robot in the course of several information time steps can be described as follows:

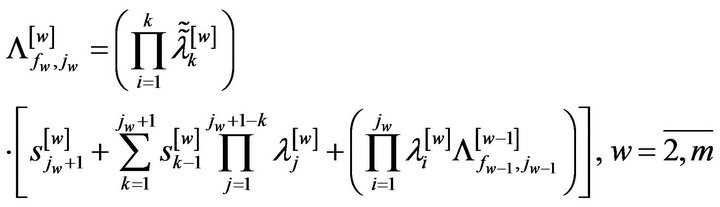
with the variables corresponding to the w-th information cycle, , the information memory coefficients of the w-th cycle for information time steps without emotions, k the information time step number, 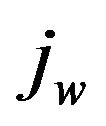the count of w-th information time steps with continuous emotional effect.

Let us introduce the following definition:

Definition 22. An information efficiency coefficient (IEC) 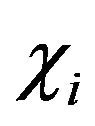is a value satisfying the relation

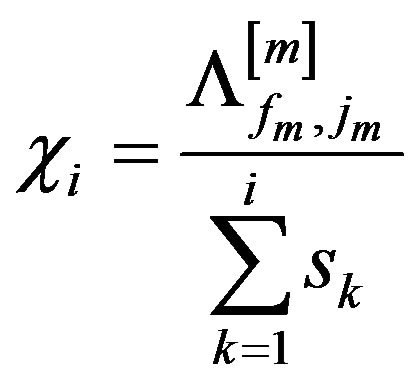with.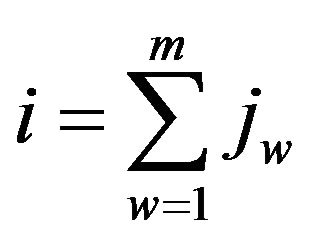

Obviously,.

It is easy to see that the closer 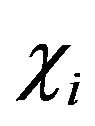to 1, the better our robot memorizes subjects.

Definition 23. A logic efficiency coefficient (LEC) is a value satisfying the relation

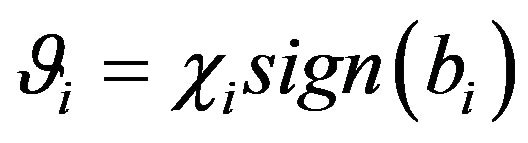
It is easy to see that 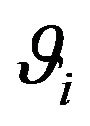satisfies.

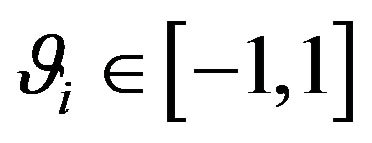When emotional perception of information effect results is positive then the logic efficiency coefficient is greater than zero; when emotional perception is negative then the logic efficiency coefficient is less than zero.

Let us consider IEC properties of the tantamountlyforgetful uniformly-informational robot. It is obvious, that 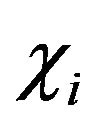for that kind of robot is defined by

(23)

Let us introduce the following theorem:

Theorem 9. The information efficiency coefficient of the uniformly-informational tantamountly-forgetful robot tends to zero under the infinite increase of information time steps.

Proof. Basing on (23), we can develop the chain of relations

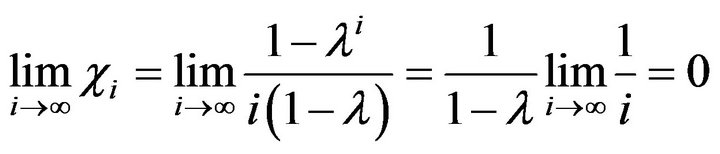
which establishes the theorem.

Now let us formulate and prove several more theorems concerning nonabsolute-information-memory robots.

Theorem 10. If there exists the number g > 0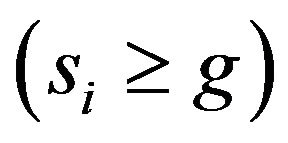, then the IEC of the robot with the nonabsolute information memory tends to zero with an infinite increase in the number of information time steps.

Proof. The chain of relations

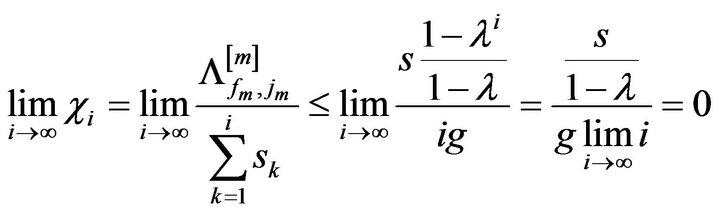
with is obvious, so the theorem is proved.

Theorem 11. If the hypotheses of Theorem 10 are satisfied then the formula is correct for robots with the nonabsolute information memory.

Proof. It is easy to see that

is valid.

According to Theorem 10 is correct, consequently

.

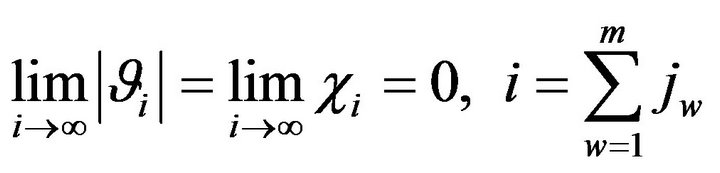The theorem is proved.

Theorems 10 and 11 may be re-phrased as follows: IEC and LEC of the robot with the nonabsolute information memory under some mild conditions in the course of time tend to zero, i.e. effectiveness of information accumulation and logic responses to data received by the robot become negligible in the course of time.

The efficiency coefficient defines first of all ability of the robot with nonabsolute memory to accumulation of information or to emotional education.

So, in this paper we gave mathematical models of robots with the nonabsolute rote memory and studied some of psychological properties of those robots. Under some assumptions of math models the obtained theoretical results enable forecasting the E-creature’s behavior.

As opposed to the existing mathematical methods which try to copy mental and emotional activity of human directly to robots, we develop a simplified model of a human analogue. But from our point of view this model enables discovering common traits of human behavior or behavior of a robot with a nonabsolute rote memory; of course, it does not take into account individual peculiarities of human psychology.

REFERENCES