Intelligent Control and Automation
Vol. 3 No. 1 (2012) , Article ID: 17563 , 15 pages DOI:10.4236/ica.2012.31001
Mathematical Reasoning of Treatment Principle Based on the Stable Logic Analysis Model of Complex Systems
School of Finance and Statistics, East China Normal University, Shanghai, China
Email: ysh_zhang@163.com
Received October 21, 2011; revised November 6, 2011; accepted November 13, 2011
Keywords: Steady Multilateral Systems; Opposite Relations; Capability of Intervention Reaction; Capability of Self-Protection; Side Effects; Medical and Drug Resistance Problem
ABSTRACT
The article reviews the stable logic analysis model of complex systems or steady multilateral systems with two noncompatibility relations. Energy concept in Physics is introduced to the multilateral systems and used to deal with the multilateral system diseases. By using mathematical reasoning, it is demonstrated that the treatment principle: “Virtual disease is to fill his mother but real disease is to rush down his son” and “Strong inhibition of the same time, support the weak” which due to the “Yin Yang Wu Xing” Theory in Traditional Chinese Medicine (TCM).
1. Introduction
The stable logic analysis model of a complex system or a steady multilateral system with two non-compatibility relations has been used in medicine, physical, finance, intelligent control and automation. Its main purpose is to investigate the structure of stable logic analysis corresponding to a general complex system.
Two stable logic analysis models of complex systems have been investigated, the causal model with compatibility relations, the causal model with non-compatibility relations. This article focuses on the causal model with non-compatibility relations.
Zhang’s theories, multilateral matrix theory [1] and multilateral system theory [2], give a new and strong mathematical reasoning method from macro (Global) analysis to micro (Local) analysis. He and his colleagues have made some mathematical models and methods of reasoning [3- 18], which make the mathematical reasoning of Traditional Chinese Science (TCS, or Oriental Science) possible [14] based on “Yin Yang Wu Xing”(阴阳五行) Theory [19]. This paper will use steady multilateral systems to demonstrate the treatment principle of Traditional Chinese Medicine (TCM): “Real disease is to rush down his son but virtual disease is to fill his mother”(实则泻其子, 虚则补其母) and “Strong inhibition of the same time, support the weak”(抑强扶弱).
The article proceeds as follows: Section 2 contains basic concepts and main theorems of steady multilateral systems while both intervention rule and self-protection rule based on the multilateral systems are demonstrated in Section 3. Some discussions are given in Section 4 and conclusions are drawn in Section 5.
2. Basic Concept of Steady Multilateral Systems
In the real world, we are enlightened from some concepts and phenomena such as “biosphere”, “food chain”, “ecological balance” etc. With research and practice, by using the theory of multilateral matrices [1] and analyzing the conditions of symmetry [1,3] and orthogonality [4-6,13,18] what a stable system must satisfy, in particular, with analyzing the basic conditions what a stable working procedure of good product quality must satisfy [12,18], we are inspired and find some rules and methods, then present the logic model of analyzing stability of complex systems [8-11]-steady multilateral systems [14,15]. There are a number of essential reasoning methods based on the stable logic analysis model, such as “transition reasoning”, “atavism reasoning”, “genetic reasoning”, etc.
2.1. Equivalent Relations
Let V be a non-empty set and define its direct product as . A non-empty subset
. A non-empty subset  is called a relation of
is called a relation of . Let
. Let 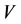 be a nonempty set with a relation
be a nonempty set with a relation . The relation
. The relation 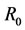 is called an equivalent relation, denoted
is called an equivalent relation, denoted  by
by , if the following three conditions are all true:
, if the following three conditions are all true:
1) Reflexive:  for all
for all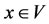 , i.e.,
, i.e.,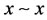 ;
;
2) Symmetric: if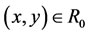 , then
, then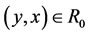 , i.e., if
, i.e., if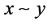 , then
, then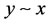 ;
;
3) Conveyable (Transitivity): if , then
, then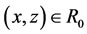 , i.e., if
, i.e., if 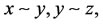 then
then 
Furthermore, the relation is called a compatibility relation if there exists a non-empty subset
is called a compatibility relation if there exists a non-empty subset  such that
such that 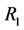 satisfies at least one of the conditions above. And the relation
satisfies at least one of the conditions above. And the relation 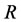 is called a non-compatibility relation if there doesn’t exist any non-empty subset
is called a non-compatibility relation if there doesn’t exist any non-empty subset 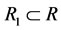 such that
such that 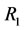 satisfies any one of the conditions above. Any one of compatibility relations can be expanded into an equivalent relation [2].
satisfies any one of the conditions above. Any one of compatibility relations can be expanded into an equivalent relation [2].
Western science only considers the reasoning under one Axiom system such that only compatibility relation reasoning is researched. However there are many Axiom systems in Nature. TCS mainly researches the generalized reasoning among many Axiom systems in Nature. Of course, she also considers the reasoning under one Axiom system but she only expands the reasoning as the equivalent relation reasoning.
2.2. Two Kinds of Opposite Relations
Equivalent relations, even compatibility relations, cannot portray the structure of the complex systems clearly. For example, assume that  and
and  are good friends and they have close relations. So are
are good friends and they have close relations. So are  and
and . However, you cannot get the conclusion that
. However, you cannot get the conclusion that 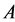 and
and  are good friends.
are good friends.
We denote  as that
as that  and
and 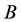 have close relations. Then the example above can be denoted as:
have close relations. Then the example above can be denoted as: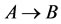 ,
, 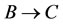 do not imply
do not imply , i.e., the relation
, i.e., the relation 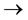 is a non-conveyable (or non-transitivity) relation, of course, a non-equivalent relation. In the following, we consider two non-compatibility relations.
is a non-conveyable (or non-transitivity) relation, of course, a non-equivalent relation. In the following, we consider two non-compatibility relations.
Let  be a nonempty set. There are two kinds of opposite relations: the neighboring relation
be a nonempty set. There are two kinds of opposite relations: the neighboring relation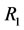 , denoted
, denoted  by
by , and the alternate relation
, and the alternate relation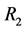 , denoted
, denoted  by
by , having the property:
, having the property:
1) If ,
,  , then
, then ;
;
 if
if ,
, 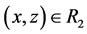 , then
, then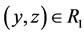 ;
;
 if
if ,
,  , then
, then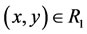 ;
;
2) If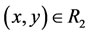 ,
, 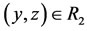 , then
, then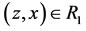 ;
;
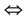 if
if ,
,  , then
, then ;
;
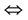 if
if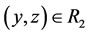 ,
, 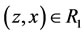 , then
, then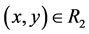 .
.
Two kinds of opposite relations cannot be exist separately. Such reasoning can be expressed in Figure 1. The first triangle reasoning is known as a jumping-transition reasoning, while the second triangle reasoning is known as atavism reasoning. Reasoning method is a triangle on both sides decided to any third side. Both neighboring relations and alternate relations are not compatibility relations, of course, none equivalent relations, called noncompatibility relations.
2.3. Genetic Reasoning
Let 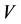 be a nonempty set and
be a nonempty set and  be not equal one
be not equal one

Figure 1. Triangle reasoning.
another. If equivalent relations, neighboring relations, and alternate relations in 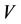 exist at the same time, then a genetic reasoning is defined as follows:
exist at the same time, then a genetic reasoning is defined as follows:
1) if
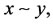 , then
, then ;
;
2) if 
 , then
, then ;
;
3) if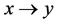 ,
,  , then
, then ;
;
4) if ,
,  , then
, then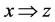 .
.
2.4. Multilateral Systems
For a nonempty set  and its some relations (nonempty sets):
and its some relations (nonempty sets):
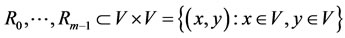
denote that , the form
, the form  (or simply, V) is called a multilateral system [2,14,15], if
(or simply, V) is called a multilateral system [2,14,15], if  satisfies the following properties:
satisfies the following properties:
1) where the notation that
where the notation that 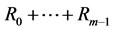 means that
means that  .
.
2) 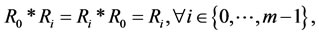
where  there is at least a
there is at least a 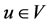 such that
such that 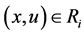 and
and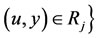 .
.
3) For any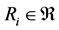 , we have
, we have , where
, where  .
.
4) For any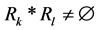 , there exists a relation
, there exists a relation 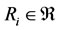 such that
such that .
.
The 4) is called the generalized reasoning, the 1) the uniqueness of reasoning, the 2) the hereditary of reasoning (or genetic reasoning) and the 3) the equivalent property of reasoning of both relations  and
and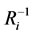 , i.e., the reasoning of
, i.e., the reasoning of  is equivalent to the reasoning of
is equivalent to the reasoning of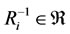 . In this case, the two-relation set
. In this case, the two-relation set 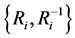 is a lateral relation of
is a lateral relation of . Furthermore, the
. Furthermore, the 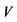 and
and 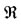 are called the state space and relationship classes considered of
are called the state space and relationship classes considered of , respectively.
, respectively.
A multilateral system  is called complex if there exists at least a non-compatibility relation
is called complex if there exists at least a non-compatibility relation . In this case, the multilateral system
. In this case, the multilateral system 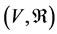 is also called a logic analysis model of complex systems [8-11].
is also called a logic analysis model of complex systems [8-11].
Assume that there exist three relations: an equivalent relation, a neighboring relation, and an alternate relation in system V, which satisfy genetic reasoning. If for any two elements , at least there is one of the three relations between
, at least there is one of the three relations between  and
and , and there are not
, and there are not 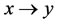 and
and 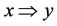 at the same time, then it is easily to prove that V is an unique multilateral system with two noncompatibility relations. The multilateral system V is also called a logic analysis model of complex systems, which is equivalent to the logic architecture of reasoning model of “Yin-Yang”(阴阳) Theory in Ancient China. In this paper, we only consider this multilateral system. There are many reasoning models in TCS which are not “YinYang “model but which are multilateral systems above. The generalized multilateral systems with many noncompatibility relations are given in [2].
at the same time, then it is easily to prove that V is an unique multilateral system with two noncompatibility relations. The multilateral system V is also called a logic analysis model of complex systems, which is equivalent to the logic architecture of reasoning model of “Yin-Yang”(阴阳) Theory in Ancient China. In this paper, we only consider this multilateral system. There are many reasoning models in TCS which are not “YinYang “model but which are multilateral systems above. The generalized multilateral systems with many noncompatibility relations are given in [2].
Theorem 2.1. For a multilateral system V with two non-compatibility relations,  , only one of the following five relations is existent and correct:
, only one of the following five relations is existent and correct:
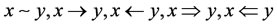 .
.
Theorem 2.2. For a multilateral system V with two non-compatibility relations,  , the following reasoning holds.
, the following reasoning holds.
1) if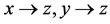 , then
, then ;
;
2) if , then
, then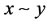 ;
;
3) if , then
, then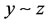 ;
;
4) if , then
, then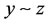 .
.
2.5. Steady Multilateral Systems
A multilateral system V is steady (or, stable) with two non-compatibility relations if there exists at least the chain circle , which satisfy at least one of the two conditions below:
, which satisfy at least one of the two conditions below:
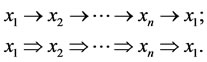 (1)
(1)
Theorem 2.3. For a steady multilateral system V with two non-compatibility relations, there exists five-length chain, and the length of the chain is integer times of 5.
Theorem 2.4. For a steady multilateral system V with two non-compatibility relations, there exists a partition of V as follows:
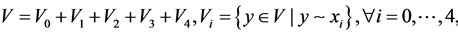
which 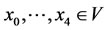 is a chain.
is a chain.
Theorem 2.5. For the decomposition above for the steady multilateral system with two non-compatibility relations, there exist relations in Figure 2.
Theorem 2.6. For each element 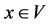 in a steady multilateral system
in a steady multilateral system 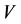 with two non-compatibility relations, there exist five equivalent classes below:
with two non-compatibility relations, there exist five equivalent classes below:

which the five equivalent classes have relations in Figure 3.

Figure 2. Uniquely steady architecture of Wu Xing.

Figure 3. The method of finding Wu Xing.
These theorems can been found in [8-11] and [14,15]. Figures 2 and 3 in Theorems 2.5 and 2.6 are the Figures of “Wu Xing”(五行) Theory in Ancient China. The steady multilateral system  with two non-compatibility relations is equivalent to the logic architecture of reasoning model of “Yin Yang Wu Xing” Theory in ancient China.
with two non-compatibility relations is equivalent to the logic architecture of reasoning model of “Yin Yang Wu Xing” Theory in ancient China.
3. Relationship Analysis of Steady Multilateral Systems
3.1. Energy of a Multilateral System
Energy concept is an important concept in Physics. Now, we introduce this concept to the multilateral systems and use these concepts to deal with the multilateral system diseases.
In mathematics, a multilateral system is said to have energy (or dynamic) if there is a none negative function φ(*) which makes every subsystem meaningful of the multilateral system.
For two subsystems  and
and 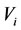 of multilateral system V, denote
of multilateral system V, denote  (or
(or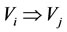 , or
, or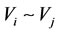 ) means
) means ,
, 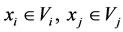 (or
(or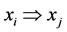 ,
, or
or ,
,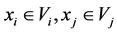 ).
).
For subsystems 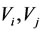 and
and 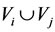 where
where ,
,
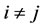 , let
, let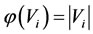 ,
, and
and
 , where
, where 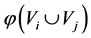 is the total energy of both
is the total energy of both  and
and .
.
For an equivalent relation , if
, if  (the normal state of the energy of
(the normal state of the energy of  ), then the equivalent relation
), then the equivalent relation  is called that
is called that  likes
likes  which means that
which means that 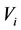 is similar to
is similar to . In this case, the
. In this case, the  is also called the brother of
is also called the brother of  while the
while the 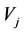 is also called the brother of
is also called the brother of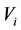 . In the causal model, the
. In the causal model, the  is called the similar family member of
is called the similar family member of 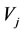 while the
while the 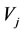 is also called the similar family member of
is also called the similar family member of . There are not any causal relation of non-compatibility considered between
. There are not any causal relation of non-compatibility considered between  and
and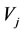 .
.
For a neighboring relation , if
, if 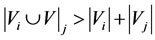 (the normal state of the energy of
(the normal state of the energy of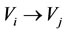 ), then the neighboring relation
), then the neighboring relation  is called that Vi bears (or loves)
is called that Vi bears (or loves)  [or that
[or that  is born (or loved) by Vi] which means that Vi is beneficial on
is born (or loved) by Vi] which means that Vi is beneficial on 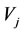 each other. In this case, the Vi is called the mother of
each other. In this case, the Vi is called the mother of  while the
while the  is called the son of Vi. In the causal model, the Vi is called the beneficial cause of
is called the son of Vi. In the causal model, the Vi is called the beneficial cause of  while the
while the 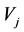 is called the beneficial effect of Vi.
is called the beneficial effect of Vi.
For an alternate relation , if
, if 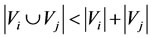 (the normal state of the energy of
(the normal state of the energy of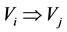 ), then the alternate relation
), then the alternate relation 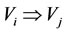 is called as that
is called as that 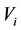 kills
kills  (or that
(or that  is killed by
is killed by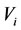 ) which means that
) which means that 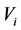 is harmful on
is harmful on 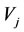 each other. In this case, the
each other. In this case, the  is called the bane of
is called the bane of 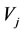 while the
while the 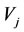 is called the prisoner of
is called the prisoner of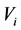 . In the causal model, the
. In the causal model, the 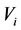 is called the harmful cause of
is called the harmful cause of 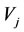 while the
while the 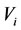 is called the harmful effect of
is called the harmful effect of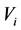 .
.
In the future, unless stated otherwise, any equivalent relation is the liking relation, any neighboring relation is the bearing relation (or the loving relation), and any alternate relation is the killing relation.
Suppose  is a steady multilateral system having energy, then during normal operation, its energy function for any subsystem of the multilateral system has an average (or expected value in Statistics), the state is called normal when the energy function is nearly to the average. Normal state is the better state.
is a steady multilateral system having energy, then during normal operation, its energy function for any subsystem of the multilateral system has an average (or expected value in Statistics), the state is called normal when the energy function is nearly to the average. Normal state is the better state.
A subsystem of a multilateral system is called not running properly (or disease, abnormal), if the energy deviation from the average of the subsystems is too large, the high [real disease (实病)] or the low [virtual disease (虚病)].
In a subsystem of a multilateral system being not running properly, if the energy of this sub-system is increased or decreased by using external forces and returned to its average (or its expected value), this method is called intervention (or making a treatment) to the multilateral system.
The purpose of intervention is to make the multilateral system return to normal state. The method of intervention is to increase or to decrease the energy of a subsystem.
What kind of treatment should follow the principle to treat it? Western science emphasizes direct treatment, but the indirect treatment of TCS is required. In mathematics, which is more reasonable?
Based on this idea, many issues are worth further discussion. For example, if an intervention treatment has been done to a multilateral system, what situation will happen?
3.2. Intervention Rule of a Multilateral System
For a steady multilateral system 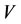 with two non-compatibility relations, suppose that there is an external force (or an intervening force) on the subsystem
with two non-compatibility relations, suppose that there is an external force (or an intervening force) on the subsystem 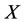 of
of 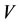 which makes the energy
which makes the energy  of
of  changed by the increment
changed by the increment , then the energies
, then the energies ,
, 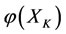 ,
, 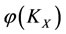 ,
,  of other subsystems
of other subsystems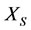 ,
,  ,
, 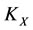 ,
, 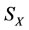 (defined in Theorem 2.6) of
(defined in Theorem 2.6) of 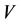 will be changed by the increments
will be changed by the increments ,
,  ,
, 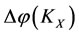 and
and 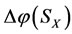 , respectively.
, respectively.
It is said that a multilateral system has the capability of intervention reaction if the multilateral system has capability to response the intervention force.
If a subsystem  of multilateral system
of multilateral system  is intervened, then the energies
is intervened, then the energies 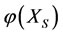 and
and 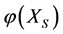 of the subsystems
of the subsystems  and
and  which have neighboring relations to
which have neighboring relations to  will change in the same direction of the force outside on
will change in the same direction of the force outside on . We call them beneficiaries. But the energies
. We call them beneficiaries. But the energies 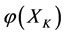 and
and  of the subsystems
of the subsystems 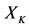 and
and 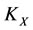 which have alternate relations to
which have alternate relations to 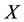 will change in the opposite direction of the force outside on
will change in the opposite direction of the force outside on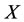 . We call them victims.
. We call them victims.
Furthermore, in general, there is an essential principle of intervention: any one of energies  and
and 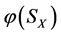 of beneficial subsystems
of beneficial subsystems 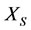 and
and 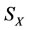 of
of  changes in the same direction of the force outside on
changes in the same direction of the force outside on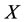 , and any one of energies
, and any one of energies 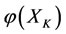 and
and 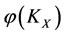 of harmful subsystems XK and
of harmful subsystems XK and 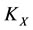 of
of  changes in the opposite direction of the force outside on
changes in the opposite direction of the force outside on . The changed size
. The changed size  (or
(or ) of the energy
) of the energy  (or
(or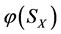 ) is equal to the size
) is equal to the size 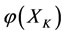 (or
(or ) of
) of 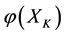 (or
(or ), but the direction opposite.
), but the direction opposite.
Intervention Rule: In the case of virtual disease, the treatment method of intervention is to increase the energy. If the treatment has been done on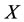 , the energy increment (or, increase degree)
, the energy increment (or, increase degree)  of the son
of the son  of
of  is greater than the energy increment (or, increase degree)
is greater than the energy increment (or, increase degree) 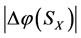 of the mother
of the mother  of
of , i.e., the best benefit is the son
, i.e., the best benefit is the son 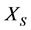 of
of . But the energy decrease degree
. But the energy decrease degree 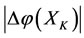 of the prisoner
of the prisoner 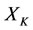 of X is greater than the energy decrease degree
of X is greater than the energy decrease degree 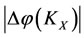 of the bane
of the bane  of X, i.e., the worst victim is the prisoner
of X, i.e., the worst victim is the prisoner 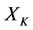 of X.
of X.
In the case of real disease, the treatment method of intervention is to decrease the energy. If the treatment has been done on X, the energy decrease degree 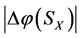 of the mother
of the mother 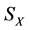 of X is greater than the energy decrease degree
of X is greater than the energy decrease degree  of the son
of the son  of
of  i.e., the best benefit is the mother
i.e., the best benefit is the mother 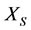 of X. But the energy increment (or, increase degree)
of X. But the energy increment (or, increase degree)  of the bane
of the bane  of X is greater than the energy increment (or, increase degree)
of X is greater than the energy increment (or, increase degree) 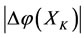 of the prisoner
of the prisoner  of
of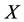 , i.e., the worst victim is the bane
, i.e., the worst victim is the bane  of
of .
.
In mathematics, the changing laws are as follows.
1) If , then
, then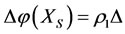 ,
,
 ,
,  ,
,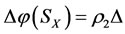 ;
;
2) If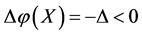 , then
, then ,
,
 ,
, 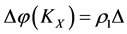 ,
,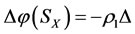 ;
;
where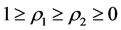 . Both
. Both  and
and  are called intervention reaction coefficients, which are used to represent the capability of intervention reaction. The larger the intervention reaction coefficient
are called intervention reaction coefficients, which are used to represent the capability of intervention reaction. The larger the intervention reaction coefficient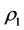 , the better the capability of intervention reaction. The state
, the better the capability of intervention reaction. The state  is the best state but the state
is the best state but the state  is the worst state.
is the worst state.
Medical and drug resistance problem is that such a question, beginning more appropriate medical treatment, but is no longer valid after a period. It is because the capability of intervention reaction is bad, i.e., the intervention reaction coefficients 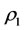 and
and 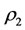 is too small. In the state
is too small. In the state , any medical and drug resistance problem is non-existence but in the state
, any medical and drug resistance problem is non-existence but in the state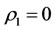 , medical and drug resistance problem is always existence. At this point, the paper advocates the principle of treatment to avoid medical and drug resistance problems.
, medical and drug resistance problem is always existence. At this point, the paper advocates the principle of treatment to avoid medical and drug resistance problems.
This intervention rule is similar to force and reaction in Physics.
3.3. Self-Protection Rule of a Multilateral System
If there is an intervening force on the subsystem  of a steady multilateral system
of a steady multilateral system 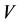 which makes the energy
which makes the energy  changed by increment
changed by increment 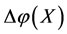 such that the energies
such that the energies 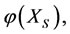
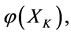

 of other subsystems
of other subsystems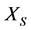 ,
,  ,
,  ,
, 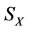 (defined in Theorem 2.6) of
(defined in Theorem 2.6) of  will be changed by the increments
will be changed by the increments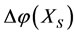 ,
,  ,
,  ,
,  , respectively, then can the multilateral system
, respectively, then can the multilateral system  has capability to protect the worst victim to restore?
has capability to protect the worst victim to restore?
It is said that the steady multilateral system has the capability of self-protection if the multilateral system has capability to protect the worst victim to restore. The capability of self-protection of the steady multilateral system is said to be better if the multilateral system has capability to protect the all victims to restore.
In general, there is an essential principle of self-protection: any harmful subsystem of X should be protected by using the same intervention force but any beneficial subsystem of 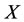 should not.
should not.
Self-protection Rule: In the case of virtual disease, the treatment method of intervention is to increase the energy. If the treatment has been done on , the worst victim is the prisoner
, the worst victim is the prisoner 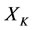 of
of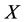 . Thus, the treatment of self-protection is to restore the prisoner
. Thus, the treatment of self-protection is to restore the prisoner 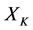 of
of  and the restoring method of self-protection is to increase the energy
and the restoring method of self-protection is to increase the energy  of the prisoner
of the prisoner  of
of 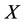 by using the intervention force on
by using the intervention force on  according to the intervention rule.
according to the intervention rule.
In the case of real disease, the treatment method of intervention is to decrease the energy. If the treatment has been done on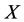 , the worst victim is the bane
, the worst victim is the bane  of
of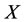 . Thus, the treatment of self-protection is to restore the bane
. Thus, the treatment of self-protection is to restore the bane 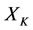 of
of  and the restoring method of self-protection is to decrease the energy
and the restoring method of self-protection is to decrease the energy  of the bane
of the bane  of
of  by using the same intervention force on
by using the same intervention force on 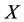 according to the intervention rule.
according to the intervention rule.
In mathematics, the following self-protection laws hold.
1) If , then the energy
, then the energy  of subsystem
of subsystem  will decrease the increment
will decrease the increment , which is the worst victim. So the capability of self-protection increases the energy
, which is the worst victim. So the capability of self-protection increases the energy 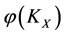 of subsystem
of subsystem  by increment
by increment  in order to restore the worst victim
in order to restore the worst victim 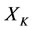 by according to the intervention rule.
by according to the intervention rule.
2) If , then the energy
, then the energy 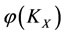 of subsystem
of subsystem  will increase the increment (
will increase the increment (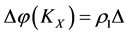 ), which is the worst victim. So the capability of self-protection decreases the energy
), which is the worst victim. So the capability of self-protection decreases the energy 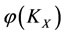 of subsystem
of subsystem , by the same size to
, by the same size to 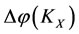 but the direction opposite, i.e., by increment (
but the direction opposite, i.e., by increment (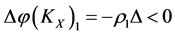 ), in order to restore the worst victim
), in order to restore the worst victim 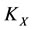 by according to the intervention rule.
by according to the intervention rule.
The self-protection rule can be explained as: the general principle of self-protection subsystem is that the worst victim is protected firstly, the protection method is in the same way to the intervention force but any beneficiary should be not protected.
Theorem 3.1. Suppose that a steady multilateral system  which has energy and capability of self-protection is with intervention reaction coefficients
which has energy and capability of self-protection is with intervention reaction coefficients 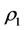 and
and . If the capability of self-protection can make the subsystem
. If the capability of self-protection can make the subsystem  to be restored, then the following statements are true.
to be restored, then the following statements are true.
1) In the case of virtual disease, the treatment method is to increase the energy. If an intervention force on the subsystem 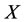 of steady multilateral system
of steady multilateral system 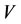 is implemented such that its energy
is implemented such that its energy 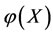 has been changed by increment
has been changed by increment , then all five subsystems will be changed finally by the increments as follows:
, then all five subsystems will be changed finally by the increments as follows:
 (2)
(2)
2) In the case of real disease, the treatment method is to increase the energy. If an intervention force on the subsystem  of steady multilateral system
of steady multilateral system  is implemented such that its energy
is implemented such that its energy 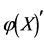 has been changed by increment
has been changed by increment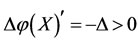 , then all five subsystems will be changed finally by the increments as follows:
, then all five subsystems will be changed finally by the increments as follows:
 (3)
(3)
where the ’s and
’s and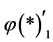 ’s are the increments under the capability of self-protection.
’s are the increments under the capability of self-protection.
Proof. 1) By according to the intervention rule, if  , then all five subsystems will be changed by increments as follows:
, then all five subsystems will be changed by increments as follows:

By according to self-protection rule, the worst victim of the subsystem  can be restored if the energy
can be restored if the energy 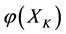 of subsystem
of subsystem  increases by increment
increases by increment . In this case, all five subsystems will be changed by according to the intervention rule as follows:
. In this case, all five subsystems will be changed by according to the intervention rule as follows:

Finally, all five subsystems will be changed by the increments in Equation (2).
2) Similarly, by according to intervention rule, if 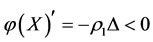 , then all five subsystems will be changed by increments as follows:
, then all five subsystems will be changed by increments as follows:

By according to self-protection rule, the worst victim subsystem  can be restored if the energy
can be restored if the energy  of subsystem
of subsystem 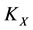 decreases by the same size, i.e., by increment
decreases by the same size, i.e., by increment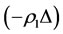 . In this case, all five subsystems will be changed by according to the intervention rule as follows:
. In this case, all five subsystems will be changed by according to the intervention rule as follows:
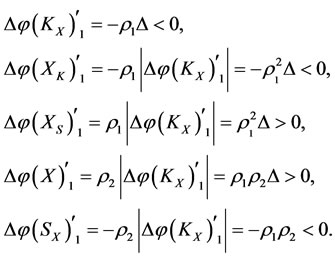
Finally, all five subsystems will be changed by the increments in Equation (3). □
Corollary 3.1. Suppose that a steady multilateral system 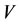 which has energy and capability of self-protection is with intervention reaction coefficients
which has energy and capability of self-protection is with intervention reaction coefficients  and
and . Then the capability of self-protection can make both subsystems
. Then the capability of self-protection can make both subsystems 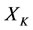 and
and 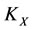 to be restored at the same time, i.e., the capability of self-protection is better, if and only if
to be restored at the same time, i.e., the capability of self-protection is better, if and only if .
.
Proof. It follows from the Theorem 3.1 directly. □
Side effects of medical problems was the question: in the medical process, destroyed the normal balance of a normal system which is not falling-ill system or intervening system. By Theorem 3.1 and Corollary 3.1, it can be seen that a necessary and sufficient condition is 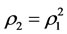 if the capability of self-protection of the steady multilateral system is better, i.e., the multilateral system has capability to protect all victims to restore. At this point, the paper advocates the principle to avoid any side effects of treatment.
if the capability of self-protection of the steady multilateral system is better, i.e., the multilateral system has capability to protect all victims to restore. At this point, the paper advocates the principle to avoid any side effects of treatment.
3.4. Mathematical Reasoning of Treatment Principle by Using the Neighboring Relations of Steady Multilateral Systems
Treatment principle by using the neighboring relations of steady multilateral systems is “Virtual disease is to fill his mother but real disease is to rush down his son”. In order to show the rationality of the treatment principle, it is needed to prove the following theorems.
Theorem 3.2. Suppose that a steady multilateral system  which has energy and capability of self-protection is with intervention reaction coefficients
which has energy and capability of self-protection is with intervention reaction coefficients 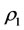 and
and 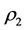 satisfying
satisfying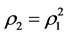 . Then the following statements are true.
. Then the following statements are true.
In the case of virtual disease, if an intervention force on the subsystem  of steady multilateral system
of steady multilateral system 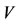 is implemented such that its energy
is implemented such that its energy 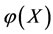 increases the increment
increases the increment , then the subsystems
, then the subsystems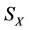 ,
, 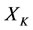 and
and 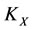 can be restored at the same time, but the subsystems
can be restored at the same time, but the subsystems  and
and 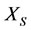 will increase their energies by the increments
will increase their energies by the increments
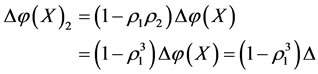
and
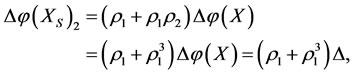
respectively.
On the other hand, in the case of real disease, if an intervention force on the subsystem 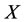 of steady multilateral system
of steady multilateral system 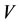 is implemented such that its energy
is implemented such that its energy  decreases, i.e., by the increment
decreases, i.e., by the increment  , the subsystems
, the subsystems ,
, 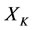 and
and  can also be restored at the same time, and the subsystems
can also be restored at the same time, and the subsystems  and
and  will decrease their energies, i.e., by the increments
will decrease their energies, i.e., by the increments
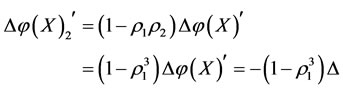
and
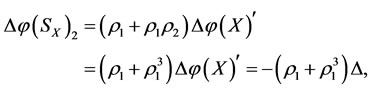
respectively.
Proof. 1) By 1) of Theorem 3.1, if the energy  of subsystem
of subsystem is also restored, then
is also restored, then 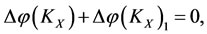 i.e.,
i.e.,  , or,
, or, 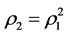 . In this case, the subsystem
. In this case, the subsystem  is also restored since
is also restored since 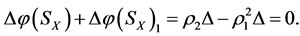
But the final increments of the energies of both subsystems  and
and 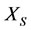 will be changed into increments
will be changed into increments 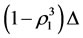 and
and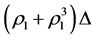 , respectively.
, respectively.
2) Similarly, by 2) of Theorem 3.1, if the energy  of subsystem
of subsystem 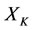 is also restored, then
is also restored, then  i.e.,
i.e.,  , or,
, or,  . In this case, the subsystem
. In this case, the subsystem 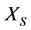 is also restored since
is also restored since 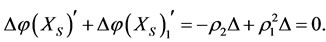
But the final increments of the energies of subsystems  and
and 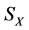 will be changed into
will be changed into 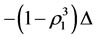 and
and  .#
.#
Theorem 3.3 For a steady multilateral system 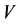 which has energy and capability of self-protection, assume intervention reaction coefficients are
which has energy and capability of self-protection, assume intervention reaction coefficients are  and
and 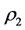 which satisfy
which satisfy 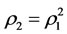 and
and 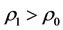 where
where  (the following the same) is the solution of
(the following the same) is the solution of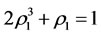 . Then the following statements are true.
. Then the following statements are true.
1) If an intervention force on the subsystem  of steady multilateral system
of steady multilateral system 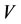 is implemented such that its energy
is implemented such that its energy  has been changed by increment
has been changed by increment  , then the final increment
, then the final increment 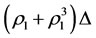 of the energy
of the energy 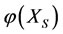 of the subsystem
of the subsystem 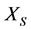 changed is greater than the final increment
changed is greater than the final increment  of the energy
of the energy  of the subsystem X changed based on the capability of self-protection.
of the subsystem X changed based on the capability of self-protection.
2) If an intervention force on the subsystem X of steady multilateral system 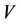 is implemented such that its energy
is implemented such that its energy 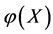 has been changed by increment
has been changed by increment 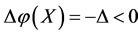 , then the final increment
, then the final increment 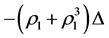 of the energy
of the energy  of the subsystem
of the subsystem  changed is less than the final increment
changed is less than the final increment  of the energy
of the energy 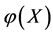 of the subsystem
of the subsystem  changed based on the capability of self-protection.
changed based on the capability of self-protection.
Proof. Let .
.
For , derivation
, derivation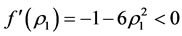 , it can be shown that
, it can be shown that  is a decrease function of
is a decrease function of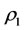 . We use SAS to solve
. We use SAS to solve 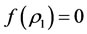 then the solution
then the solution  . So
. So  while
while . Thus
. Thus  and,
and,
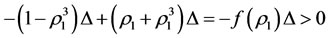 . □
. □
Corollary 3.2. For a steady multilateral system V which has energy and capability of self-protection, intervention reaction coefficients are 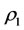 and
and  which satisfy
which satisfy 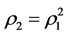 and
and . Then the following statements are true.
. Then the following statements are true.
1) In the case of virtual disease, if an intervention force on the subsystem  of steady multilateral system
of steady multilateral system  is implemented such that its energy
is implemented such that its energy 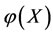 has been changed by increment
has been changed by increment , then the final increment
, then the final increment  of the energy
of the energy  of the subsystem
of the subsystem 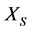 changed is less than the final increment
changed is less than the final increment 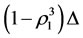 of the energy
of the energy 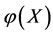 of the subsystem
of the subsystem 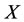 changed based on the capability of self-protection.
changed based on the capability of self-protection.
2) In the case of real disease, if an intervention force on the subsystem  of steady multilateral system V is implemented such that such that its energy
of steady multilateral system V is implemented such that such that its energy  has been changed by increment
has been changed by increment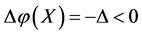 , then the final increment
, then the final increment  of the energy
of the energy 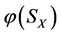 of the subsystem
of the subsystem 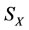 changed is greater than the final increment
changed is greater than the final increment 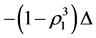 of the energy
of the energy 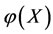 of the subsystem
of the subsystem  changed based on the capability of self-protection.
changed based on the capability of self-protection.
Proof. It follows from the Theorem 3.2 directly.
3.4.1. Treatment Principle If Only One Subsystem of the Steady Multilateral System Falls Ill
Suppose that only one subsystem 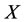 is abnormal (or disease ), i.e., its energy is too high or too low. It can be shown by Theorems 3.1 and 3.2 that if intervention reaction coefficients satisfy
is abnormal (or disease ), i.e., its energy is too high or too low. It can be shown by Theorems 3.1 and 3.2 that if intervention reaction coefficients satisfy  and
and , then it is known that if one wants to restore the abnormal subsystem
, then it is known that if one wants to restore the abnormal subsystem , the one should not intervene subsystem
, the one should not intervene subsystem 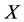 directly. The one should increase the energy of subsystem
directly. The one should increase the energy of subsystem 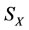 if the energy
if the energy 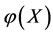 of subsystem
of subsystem  is too low. It means “Virtual disease is to fill his mother”. And one should decrease the energy of subsystem
is too low. It means “Virtual disease is to fill his mother”. And one should decrease the energy of subsystem  if the energy
if the energy  of subsystem
of subsystem 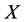 is too high. It means “Real disease is to rush down his son”.
is too high. It means “Real disease is to rush down his son”.
Otherwise, under the law of self-protection, positive incremental intervention subsystem 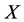 increases the energy of subsystem
increases the energy of subsystem  but the energies of other subsystems do not change; and negative incremental intervention subsystem
but the energies of other subsystems do not change; and negative incremental intervention subsystem 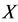 decreases the energy of subsystem
decreases the energy of subsystem 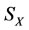 but the energies of other subsystems do not change.
but the energies of other subsystems do not change.
If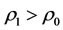 , i.e.,
, i.e.,  , then the capability of intervention reaction of the intervening subsystem is said to be normal since in this case the energy for the intervening subsystem can almost transmit to other subsystems which have neighboring relations or alternate relations with the intervening subsystem.
, then the capability of intervention reaction of the intervening subsystem is said to be normal since in this case the energy for the intervening subsystem can almost transmit to other subsystems which have neighboring relations or alternate relations with the intervening subsystem.
The capability of intervention reaction and the capability of self-protection are different from each other. After intervening, it is said the capability of self-protection of the multilateral system is normal if the final energy does not change rapidly. By using Theorem 3.2, the capability of self-protection can restore the 3 subsystems of all 5 subsystems of  under any intervention reaction coefficients. Therefore the better capability of selfprotection should be true for most multilateral systems. By using Theorems 3.1 and 3.2 and Corollary 3.1, however, the capability of intervention reaction can affect the choice of intervention subsystems of
under any intervention reaction coefficients. Therefore the better capability of selfprotection should be true for most multilateral systems. By using Theorems 3.1 and 3.2 and Corollary 3.1, however, the capability of intervention reaction can affect the choice of intervention subsystems of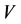 .
.
In fact, by Theorem 3.2, it will be better if we intervene subsystem 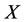 indirectly while
indirectly while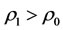 . The intervention method can be to maintain the balance of multilateral systems because only both the disease system and the intervened system are treated by using Theorem 3.2 such that there is not any side effect for all other subsystems. And the intervention method can also be to enhance the capability of intervention reaction because the method of using intervention reaction makes the
. The intervention method can be to maintain the balance of multilateral systems because only both the disease system and the intervened system are treated by using Theorem 3.2 such that there is not any side effect for all other subsystems. And the intervention method can also be to enhance the capability of intervention reaction because the method of using intervention reaction makes the 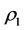 greater and near to 1. The state
greater and near to 1. The state  is the best state of the steady multilateral system. On the way, it almost have not medical and drug resistance problem since any medicine is possible good for some large
is the best state of the steady multilateral system. On the way, it almost have not medical and drug resistance problem since any medicine is possible good for some large .
.
All in all, the steady multilateral system satisfies the intervention rule and the self-protection rule. It is said healthy while the intervention reaction coefficient  satisfies
satisfies . In logic and practice, it’s reasonable
. In logic and practice, it’s reasonable 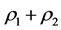 near to 1. In case:
near to 1. In case: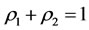 , all the energy for intervening subsystem can transmit to other subsystems which have neighboring relations or other subsystems with the intervening subsystem. The healthy condition
, all the energy for intervening subsystem can transmit to other subsystems which have neighboring relations or other subsystems with the intervening subsystem. The healthy condition  can be satisfied when
can be satisfied when  for a steady multilateral system since
for a steady multilateral system since  implies
implies  . Interestingly, it is the golden number, i.e., in general, the intervention reaction coefficient
. Interestingly, it is the golden number, i.e., in general, the intervention reaction coefficient  is nearly to the golden number 0.618 for a healthy body. If this assumptions is set up, then the treatment principle: “Real disease is to rush down his son and virtual disease is to fill his mother” based on “Yin Yang Wu Xing” Theory in TCM, is quite reasonable.
is nearly to the golden number 0.618 for a healthy body. If this assumptions is set up, then the treatment principle: “Real disease is to rush down his son and virtual disease is to fill his mother” based on “Yin Yang Wu Xing” Theory in TCM, is quite reasonable.
But, by Corollary 3.2, it will even be better if we intervene subsystem 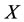 itself directly for a bad body in the case that
itself directly for a bad body in the case that 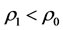 where
where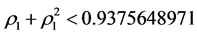 . It can be explained that if a multilateral system which has a poor capability of intervention reaction, then it is better to intervene the subsystem itself directly than indirectly. The intervention method, however, always destroy the balance of multilateral systems because there exists at least one energy of both the mother and the son of the intervened system changed by Theorem 3.2 such that there is at least one side effects: the mother or the son corresponding to real disease or virtual disease, respectively. And the intervention method also have harmful to the capability of intervention reaction because the method which don’t use the capability of intervention reaction makes the
. It can be explained that if a multilateral system which has a poor capability of intervention reaction, then it is better to intervene the subsystem itself directly than indirectly. The intervention method, however, always destroy the balance of multilateral systems because there exists at least one energy of both the mother and the son of the intervened system changed by Theorem 3.2 such that there is at least one side effects: the mother or the son corresponding to real disease or virtual disease, respectively. And the intervention method also have harmful to the capability of intervention reaction because the method which don’t use the capability of intervention reaction makes the 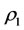 less and near to 0. The state
less and near to 0. The state 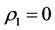 is the worst state of the steady multilateral system. On the way, the medical and drug resistance problem will be occurred since any medicine is possible too little for some small
is the worst state of the steady multilateral system. On the way, the medical and drug resistance problem will be occurred since any medicine is possible too little for some small . Therefore the intervention method directly can be used in case
. Therefore the intervention method directly can be used in case 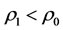 but should be used as little as possible.
but should be used as little as possible.
3.4.2. Treatment Principle if Only Two Subsystems with the Neighboring Relation of the Steady Multilateral System Encounter Sick
Suppose that the subsystems  and
and 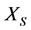 are abnormal (or diseases). In the multilateral system of relations between two non-compatible with the constraints, only two situations may occur:
are abnormal (or diseases). In the multilateral system of relations between two non-compatible with the constraints, only two situations may occur:
1)  encounters virtual disease, and at the same time,
encounters virtual disease, and at the same time, 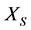 befalls virtual disease, i.e., the energy of
befalls virtual disease, i.e., the energy of 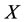 is too low and the energy of
is too low and the energy of 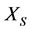 is also too low. It is because
is also too low. It is because  bears
bears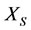 . The disease causal is
. The disease causal is .
.
2)  encounters real disease, and at the same time,
encounters real disease, and at the same time, 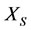 befalls real disease, i.e., the energy of
befalls real disease, i.e., the energy of  is too high and the energy of
is too high and the energy of 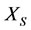 is also too high. It is because
is also too high. It is because 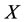 bears
bears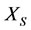 . The disease causal is
. The disease causal is .
.
It can be shown by Theorem 3.2 that if intervention reaction coefficients satisfy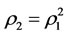 , then the following statements are true.
, then the following statements are true.
1) If one wants to treat the abnormal systems  and
and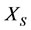 , then for virtual disease, the one should intervene subsystem
, then for virtual disease, the one should intervene subsystem 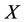 directly by increasing its energy. It means “virtual disease is to fill his mother” because the disease causal is
directly by increasing its energy. It means “virtual disease is to fill his mother” because the disease causal is .
.
2) If one wants to treat the abnormal systems 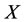 and
and , then for real disease, the one should intervene subsystem
, then for real disease, the one should intervene subsystem 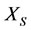 directly by decreasing its energy. It means “Real disease is to rush down his son” because the disease causal is
directly by decreasing its energy. It means “Real disease is to rush down his son” because the disease causal is .
.
The intervention method can be to maintain the balance of multilateral systems because only two disease systems are treated, by using Theorem 3.2, such that there is not any side effect for all other subsystems. And the intervention method can also be to enhance the capability of intervention reaction because the method of using the capability of intervention reaction makes the 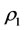 greater and near to 1. The state
greater and near to 1. The state 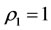 is the best state of the steady multilateral system. On the way, it almost have not medical and drug resistance problem since any medicine is possible good for some large
is the best state of the steady multilateral system. On the way, it almost have not medical and drug resistance problem since any medicine is possible good for some large .
.
In order to use the treatment principle of neighboring relations, similar to TCM, we can assume that real disease and virtual disease have their reasons. Real disease is caused by the born subsystem and virtual disease is caused by the bear subsystem. Although the reason can not be proved easily in mathematics or experiments, the treatment method under the assumption is quite equal to the treatment method in the intervention indirectly.
3.5. Mathematical Reasoning of Treatment Principle by Using the Alternate Relations of Steady Multilateral Systems
Treatment principle by using the alternate relations of steady multilateral systems is “Strong inhibition of the same time, support the weak”. In order to show the rationality of the treatment principle, it needed to prove the following theorem.
Theorem 3.4. Suppose that a steady multilateral system  which has energy and capability of self-protection is with intervention reaction coefficients
which has energy and capability of self-protection is with intervention reaction coefficients  and
and 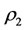 which satisfying
which satisfying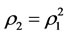 . Assume there are two subsystems
. Assume there are two subsystems 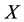 and
and 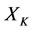 of
of  with an alternate relation such that
with an alternate relation such that 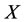 encounters virtual disease, and at the same time,
encounters virtual disease, and at the same time, 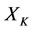 befalls real disease. Then the following statements are true.
befalls real disease. Then the following statements are true.
If an intervention force on the subsystem 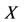 of steady multilateral system
of steady multilateral system 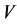 is implemented such that its energy
is implemented such that its energy 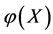 has been changed by increment
has been changed by increment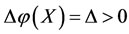 , and at the same time, another intervention force on the subsystem
, and at the same time, another intervention force on the subsystem  of steady multilateral system
of steady multilateral system 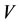 is also implemented such that its energy
is also implemented such that its energy  has been changed by increment
has been changed by increment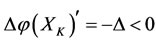 , then all other subsystems:
, then all other subsystems: ,
, 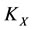 and
and  can be restored at the same time, and the subsystems
can be restored at the same time, and the subsystems  and
and  will increase and decrease their energies by the same size but the direction opposite, i.e., by the increments
will increase and decrease their energies by the same size but the direction opposite, i.e., by the increments

and
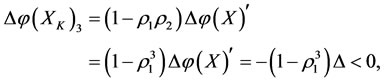
respectively.
Proof. By Theorem 3.1 in 1) and 2), we have

and

Composing these two conclusions, we get
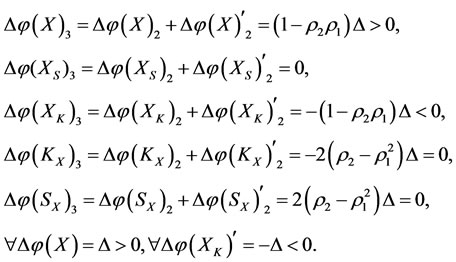
The proof is completed. □
Treatment Principle If Only Two Subsystems with the Alternate Relation of the Steady Multilateral System Encounter Sick
Suppose that the subsystems 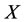 and
and 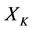 are abnormal (or disease). In the multilateral system of relations between two non-compatible with the constraints, only a situation may occur:
are abnormal (or disease). In the multilateral system of relations between two non-compatible with the constraints, only a situation may occur:  encounters virtual disease, and at the same time,
encounters virtual disease, and at the same time,  befalls real disease, i.e., the energy of
befalls real disease, i.e., the energy of  is too low and the energy of
is too low and the energy of  is too high, because it is normal when
is too high, because it is normal when  kills
kills 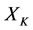 but it is abnormal when
but it is abnormal when 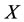 doesn’t kill
doesn’t kill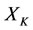 .
.
It can be shown by Theorem 3.4 that if intervention reaction coefficients satisfy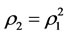 , then one should intervene subsystem
, then one should intervene subsystem 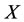 directly by increasing its energy, and at the same time, intervene subsystem
directly by increasing its energy, and at the same time, intervene subsystem  directly by decreasing its energy if the one wants to treat the abnormal systems
directly by decreasing its energy if the one wants to treat the abnormal systems  and
and . It means that “Strong inhibition of the same time, support the weak”.
. It means that “Strong inhibition of the same time, support the weak”.
The intervention method can be to maintain the balance of multilateral systems because only two disease systems are treated, by using Theorem 3.4, such that there is not any side effect for all other subsystems. And the intervention method can also be to enhance the capability of intervention reaction because the method of using the capability of intervention reaction makes that the subsystem  can kill
can kill  such that the
such that the  is greater and near to 1. The state
is greater and near to 1. The state 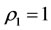 is the best state of the steady multilateral system. On the way, it almost have none medical and drug resistance problem since any medicine is possible good for some large
is the best state of the steady multilateral system. On the way, it almost have none medical and drug resistance problem since any medicine is possible good for some large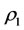 .
.
4. Discussions
The fundamental issues of any complex system are the problems of stability. But for many stable problems, the usual methods in Western science can not be used (see [20]). In this case, however, many methods in TCS can be always done.
For example, it is will known that Western medicine is in the microscopic approach to disease and always make directly medical treatments on disease organs. By Theorems 3.1, 3.2, 3.3 and 3.4 in this paper, it can be found that the method always destroys the original human being’s balance and has none beneficial to human’s immunity. Western medicine can produce pollution to human’s body, having strong side effects. Excessively using medicine can easily paralysis the human’s immunity, which AIDS is a product of Western medicine. Using medicine too little can easily produce the medical and drug resistance problem.
But TCM studies the world in the macro point of view and always makes indirectly medical treatments on disease organs. By Theorems 3.1, 3.2, 3.3 and 3.4 in this paper, it can be found that the method’s target is in order to maintain the original balance of human being and in order to enhance the immunity. TCM believes that each medicine have one-third of drug. She never encourages patients to use medicine in long term. TCM has over 5000-year history. It almost has not side effects or medical and drug resistance problem.
The mainly difference between TCS and Western Science is that Western science only considers Axiom (or Hypothesis) but TCS doesn’t. The key to intelligent control and automation should be to study the issues of nonAxiom (or non-Hypothesis). This paper’s drawbacks are just in order to solve these problems. The ideas are due to TCS.
Problems, Results and Comparisons
1) What is “Stable”? Western Science defined it as “A price or rate which changes only slowly, opposite of volatile.” But in TCS, it is specifically defined as that there is at least a causal chain (defined in (1) of Section 2.5) in a system such that the system can be survival. The definition given in TCS, for a relatively stable complex system, is most essential. If there is not the chain or circle, then will be some elements without causes or some elements without results in the system. Thus, this system is to be in the state of finding its results or causes, and there is not any stability to say.
Liao, et al. [20] has proved that for the problems of stability, many methods in Western Science can not work. Such as analysis of variance (ANOVA), regression analysis, non-five index method, etc. But a lot of methods due to TCS can be used to solve the stable center of any high-dimensional function. Such as, the global sensitivity analysis based on ANOVA [21], the Global-Local algorithm [12] and the procedure of searching zero effects [22], etc. The works were received the prestigious Science Advance First-Degree Prize of China Army in 2006.
2) What is “complex system”? Western Science defined it as “Consisting of many diverse and autonomous but interrelated and interdependent components or parts linked through many (dense) interconnections. Complex systems cannot be described by a single rule and their characteristics are not reducible to one level of descripon. They exhibit properties that emerge from the interaction of their parts and which cannot be predicted from the properties of the parts”. But in TCS, it is specifically defined as a system which has at least one non-compatibility relation in a logic analysis model of a system— multilateral system [2,15] (Defined in Section 2.4).
It is will known that the body of human is a complex system. But in Western Medicine, the existence of both side effects or medical and drug resistance problems proves it non-reasonable to some extent. But in TCM, there exist a lot of good methods to solve the problems of human body, such as theories of “Wu Yun Liu Qi”(五运六气, environment of energy), “Jing Luo”(经络, meridian/ hannel system),” “Zang Xiang”(藏象 or 脏腑, Zang Fu organ), etc. We [7-12,14-17] want to study the complex system by using these methods in TCS instead of the ones in Western science, such as “emergence”, “control”, “model”, “distribution”, and so on. It is because the methods in Western science only involved the compatibility relations under one Axiom system, and only concern how to attain the energy of complex system through study or observations at the position of standing on our own but do not show how to afford the energy for the complex system through logic or practice.
3) What is “Science”? Western science defined it as “knowledge attained through study or practice” but TCS only considers it specifically and carefully as “knowledge about energy attained and afford”. Only to know how to attain energy at the position of standing on our own but not to know how to afford energy is not a complete “Science”. What can kill the “Science” is need to know and need to protect it as more as possible. One can do by logic or practice but only by observations.
For example [14], Western Medicine is different from TCM because the TCM has a concept of Chi (or Qi, 气) as a form of energy. It is believed that this energy exists in all things (living and non-living) including air, water, food and sunlight. Chi is said to be the unseen vital force that nourishes one’s body and sustains one’s life. It is also believed that an individual is born with an original amount of Chi at the beginning of one’s life and as one grows and lives, one acquires Chi from eating and drinking, from breathing the surrounding air and also from living in one’s environment. And the one also affords Chi for the human body’s Meridian/hannel system and Zang Fu organ which form a parasitic system of human, called the second physiological system of human. The second system of human controls the first physiological system (anatomy system) of human. An individual would become ill or dies if one’s Chi in the body is imbalanced or exhausted. The concept is summarized as the energy theory of multilateral systems (Defined in Section 3.1). But there do not exist these concepts in Western science.
4) What is “Axiom”? Western Science considers it as “Hypothesis” but TCS considers it specifically and carefully as “Tao(Yin and Yang)”(道(阴和阳)), anything can be decomposed into two parts which have two kinds of opposite relations), or “You Sheng Yu Wu”(有生于无, anything is born by nothing), or “Bu Yan Shi Jiao”(不言施教, teaching cannot be made by suppose).
Lao Tzu, was one of the earliest philosopher in the Chinese history, who describes the marvel of Tao as an evolving force that operates throughout the universe. Tao is the first cause of the universe. Lao Tzu said that Tao is ‘the way’ and he emphasized this in the first verse of his Tao Teh Ching [23] that: “道可道, 非常道, 名可名, 非常名, 无名天地之始, 有名万物之母 (老子道德经, 第一章)”.
Translated as:
“The Tao that can be said is not the everlasting Tao.
If a name can be named, it is not the everlasting name.
That which has no name is the origin of heaven and earth;
That which has a name is the mother of all things”.
(Lao Tzu’s Tao Teh Ching, Verse.1) [24].
Therefore Tao is always without a name and that it is the origin of heaven and earth. Tao can also be said to be the “Absolute” that it can be said to be the movement and a stillness without a beginning, Yin and Yang (also known as Tai Chi in Figure 4) are things that can be said to be without a beginning.
The Tai Chi (Ultimate Principle of Existence) involved “The two dynamic powers” (the white space represents the Yang and the black space represents the Yin) exists in equilibrium and from which a coordinated and vigorous force is produced. This classic symbol for Yin and Yang appears like a pair of fish swimming in a circle around

Figure 4. Tai chi diagram.
each other; the tail of one is formed from the head of the other. Here, we can see that Yin-Yang are born out of each other and are transformed into each other. Each of the Yin-Yang contains the seed of the other; there is a tiny seed circle of dark Yin contained in the white part of Yang, as there is a seed circle of white Yang contained in the darkness of Yin. Tao is the force, which flows through all lives. Each person is to nurture the breathing or what is also known as the integral life force (“Chi” or “Qi”) that has been given to him/her. Unlike Western thinking, time is not linear but cyclical. And overall, each and every Taoism believer’s goal is to align him(her)self, by having a balance (the perfect sense of balance is embodied in the idea of Yin Yang) or being harmonious with the Tao.
In the universe, there should always be a balance of nature. Yin (female) and Yang (male) are always at work, and there should be a good balance between them; and hence the avoidance of extremes. This is indeed what the concept of TCS, which is anchored in Taoism roots, is summarized as the multilateral systems (Defined in Section 2.4) (see [2,14]).
5) What is “reasoning”? Western Science considers it as the reasoning under one Axiom system such that only compatibility relation reasoning researched on. But TCS mainly researches the reasoning among many Axiom systems in nature (or do not consider any Axiom system or see it nothing, or “You Sheng Yu Wu”(有生于无), anything is born by nothing) and mainly considers the noncompatibility relations between different Axioms. The noncompatibility relations are more important than compatibility relations if they are considered at same time. Lao Tzu reputed the condition of reasoning to be “Bu Zi Sheng”(不自生, not their own definition, then their reasoning and research ).
We have seen simple example of reasoning. If we know: Robins are birds. All birds have wings (Axiom). Then if we ask: Do robins have wings? “Yes”. Some reasoning (albeit very simple) has to go on answer the question. But, in TCS, one believes that Robins which are birds may be not to have wings. The one believes that the Axiom system may be not true because the Axiom is our Hypothesis or observations and there may be other Axiom system in which birds have not wings. The one mainly considers the relationship between the birds and its energies.
In general, any multilateral system (defined in Section 2.4) is a reasoning model in TCS because it is defined by a set, which is independent of the reasoning procedure, and not defined by the reasoning itself. But in Western science, almost all reasoning is defined by itself, for example, by one Axiom system obtained by observations. In other words, it is born by itself.
6) What is “causal model”? Western science defined it as “Estimating approach based on the assumption that future-value of a variable is a mathematical function of the values of other variable(s). Used where sufficient his torical data is available, and the relationship (correlation) between the dependent variable to be forecasted and associated independent variable(s) is well known”. But TCS mainly researches the causal model among many Axiom systems in Nature and mainly considers the causal model of non-compatibility relations which is more important than ones of compatibility relations if they are considered at same time. In other words, TCS mainly considers the causal among three relations, such as “Yang” relation: the neighboring relations, as beneficial, harmony, obedient, loving, etc.; “Yin” relation: alternate relations, as harmful, conflict, ruinous, killing, etc.; as well as a general equivalent category, “Tong Lei”(同类): the compatibility relation but seeing it as an equivalent relation, as similarly, family, brother, under the same Axiom system, etc.
Zhang, et al. [2,8-11] first consider the stable structure of the logic model with causal effects between two noncompatibility relations which is similar to the theory of “Yin Yang Wu Xing” in TCS. The concept of causal model has been further explained and extended to construct the generalized causal model—multilateral system (Defined in Section 2.4) in this paper. There exists none the idea in Western science.
7) What is “symmetry”? The outstanding mathematician Hermann Weil highly evaluated the role of symmetry in modern science: “Symmetry, as though is wide or narrow we did not perceive this word, there is the idea, with the help of which a man attempted to explain and to create the order, beauty and perfection”. But in TCS, it is simply defined as the neighboring relations (Defined in Section 2.2).
Global sensitivity analysis in symmetry has been first considered in [1]. Any high-dimensional function can be decomposed into a sum of some symmetrical functions based on the systems of orthogonal idempotents [3] such that these symmetrical functions are orthogonal one another [21]. The methods due to TCS can be also used to solve the causal problems of the neighboring relations (Defined in Section 2.2), such as global sensitivity analysis in symmetry based on ANOVA [1,21], Global-Local Algorithm in symmetry [1,12] and procedure of searching zero effects in symmetry [22], and so on. But there exists none the idea in Western science.
8) What is “orthogonal”? Western science defined it as “In geometry, orthogonal means ‘involving right angles’ (from Greek ortho, meaning right, and gon meaning angled). The term has been extended to general use, meaning the characteristic of being independent (relative to something else). It also can mean: non-redundant, nonoverlapping, or irrelevant. In computer terminology, something—such as a programming language or a data object—is orthogonal if it can be used without consideration as to how its use will affect something else”. But in TCS, it is simply defined as the alternate relations (Defined in Section 2.2).
Global sensitivity analysis in orthogonality has been also first considered in [1]. Any function with high-dimensional variable can be decomposed into a sum of functions with low-dimensional variable such that these functions are orthogonal one another. The methods due to TCS can be used to solve the causal problems of the alternate relations, such as Global sensitivity analysis in orthogonality based on ANOVA [1,21], Global-Local algorithm in orthogonality [1,12] and procedure of searching zero effects in orthogonality [22], and so on.
Western science studied the global sensitivity analysis in orthogonality by using the methods of Monte Carlo and quasi-Monte Carlo algorithms. Wang et al. [18] have proved that the method of using orthogonal arrays is more optimal than those in Western science. The procedure in [18] is due to the theories of the “Yi Jing”(《易经》), the “Ming Xiang”(命相) and the “Fend Shui”(风水) of China.
Construction of orthogonal arrays in Western science is always to use the theory of group. But in TCS, the images concept of Lao Tzu is considered as the origin or beginning of anything. Similarly to the images of Tao, many new concepts have been found, such as, matrix images [4], generalized difference matrices [25] and generalized orthogonal arrays [26] (orthogonal balance block design [1], or balance block orthogonal arrays [27]), and so on. Many new constructing methods of orthogonal arrays have been obtained, such as add, subtract, multiply, divide and replace. They are composed of five classes [4-6,12,13] by the idea of “Wu Xing”. We believe they are all ones because by Theorem 2.5 all complex system can be decomposed into five classes with non-compatibility relations. The works were received the prestigious Innovative Teaching and Technology First-Degree Prize of China in 2010.
9) What is “Intelligent”? Western science defined it as “Intelligence is the system’s level of performance in reaching its objectives”. But in TCS, it is simply defined as the system’s level of performance in order to know the laws or images of the Tao.
In TCS, the intelligent knowledge mainly is due to the Tao Teh Ching and the “Yi Jing”. The Tao Teh Ching is a logic model and the “Yi Jing” is a reasoning model. Zhang [1] first studies the mathematical logic reasoning structure of Tao Teh Ching, called theory of multilateral systems [2] (Defined in Section 2.4) and the mathematical algorithm reasoning structure of “Yi Jing”, called theory of multilateral matrices [1]. Based on these, many new procedures which are due to TCS have been obtained, such as, the global sensitivity analysis based on ANOVA [21], Global-Local algorithm [12] and procedure of searching zero effects [22], and so on. Both the multilateral matrices and the multilateral systems are the foundation for studying the intelligent knowledge in TCS.
10) What is “Control”? Western science defined it as “Management process in which the (1) actual performance is compared with planned performance, (2) difference between the two is measured, (3) causes contributing to the difference are identified, and (4) corrective action is taken to eliminate or minimize the difference”. But in TCS, it is simply defined as the intervention (making a treatment) on a complex system (Defined in Section 3.2).
In Chinese, the control concept is mainly due to the theory of “Yin Yang Wu Xing”, which doesn’t consider the function model to control but control by using five indexes:
Wood (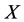 ), fire
), fire , earth
, earth , metal
, metal  and water
and water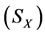 , where there exist two kinds of opposite non-compatibility relations among the five subsets. Zhang, et al. [7] have studied the statistical estimating methods of the five indexes and Zhang [12] has given the proofs of the theory and obtained a lot of algorithms from Global to Local controlling by using the five indexes, called GL algorithm. Luo et al. [28] has further explained its applications in the turning point analysis of finance time series. Treatment principle of intervention (Defined in Section 3) in this paper is the foundation for controlling.
, where there exist two kinds of opposite non-compatibility relations among the five subsets. Zhang, et al. [7] have studied the statistical estimating methods of the five indexes and Zhang [12] has given the proofs of the theory and obtained a lot of algorithms from Global to Local controlling by using the five indexes, called GL algorithm. Luo et al. [28] has further explained its applications in the turning point analysis of finance time series. Treatment principle of intervention (Defined in Section 3) in this paper is the foundation for controlling.
11) What is “Automation”? The dictionary defines automation as “the technique of making an apparatus, a process, or a system operate automatically.” But in TCS, it is specifically and carefully defined that one can establish a system such that it can run naturally only by using the capability of self-protection of the system (Defined in Section 3.3), i.e., it is wu wei er wu bu wei (无为而无不为)-by doing nothing, everything is done.
In Chinese, the automation concept is mainly due to the Taoism believer’s idea. The idea is to set a causal circle (circle of Tao) on a system, i.e.wood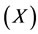 )
)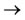 fire
fire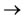
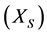 earth
earth
 metal
metal
 water
water
 wood
wood
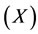 ···where there exist two kinds of opposite non-compatibility relations among the five subsets. Any nature system of objects has its energy and its capability of self-protection. If one wants to obtain the system’s energy, the system’s capability of self-protection will work. If the one can establish a causal circle above on the system such that it can run naturally only by using the nature force of a causal circle or the capability of self-protection, the one may be doing nothing but everything is done. The method is called “Tao Fa Zi Ran”(道法自然, imitation of Nature).
···where there exist two kinds of opposite non-compatibility relations among the five subsets. Any nature system of objects has its energy and its capability of self-protection. If one wants to obtain the system’s energy, the system’s capability of self-protection will work. If the one can establish a causal circle above on the system such that it can run naturally only by using the nature force of a causal circle or the capability of self-protection, the one may be doing nothing but everything is done. The method is called “Tao Fa Zi Ran”(道法自然, imitation of Nature).
In order to implement above idea, we must test first the structure of computer’s language whether it satisfies the circle’s conditions or not and make a causal circle above. Zhang et al. [29] have studied the structure of SAS language and found it satisfying the circle’s conditions to some extent. A lot of computer automated program templates have given in [29], such as automated modeling (zero component search), automated simulation, GL algorithm, automated prediction, automatic calculation, etc. The intervention rule and self-protection rule in this paper are the foundation of these methods.
5. Conclusions
This work shows how to treat the diseases of a steady multilateral system and three methods are presented.
If only one subsystem falls ill, mainly the treatment method should be to intervene it indirectly for case: the capability coefficient 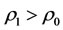 of intervention reaction, according to the treatment principle of “Real disease is to rush down his son but virtual disease is to fill his mother”. The intervention method directly can be used in case
of intervention reaction, according to the treatment principle of “Real disease is to rush down his son but virtual disease is to fill his mother”. The intervention method directly can be used in case 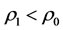 but should be used as little as possible.
but should be used as little as possible.
If two subsystems with the neighboring relation encounter sick, the treatment method should be intervene them directly also according to the treatment principle of “Real disease is to rush down his son but virtual disease is to fill his mother”.
If two subsystems with the alternate relation encounter sick, the treatment method should be intervene them directly also according to the treatment principle of “Strong inhibition of the same time, support the weak”.
Other properties of steady multilateral systems, such as balanced, orderly nature, and so on, will be discussed in the next articles.
6. Acknowledgements
This article has been repeatedly invited as reports, such as People’s University of China in medical meetings, Shanxi University, Xuchang College, and so on. The work was supported by Specialized Research Fund for the Doctoral Program of Higher Education of Ministry of Education of China (Grant No.44k55050).
REFERENCES
- Y. S. Zhang, “Multilateral Matrix Theory,” Chinese Stat. Press, 1993. http://www.mlmatrix.com
- Y. S. Zhang, “Theory of Multilateral Systems,” 2007. http://www.mlmatrix.com
- Y. S. Zhang, S. Q. Pang, Z. M. Jiao and W. Z. Zhao, “Group Partition and Systems of Orthogonal Idempotents,” Linear Algebra and Its Applications, Vol. 278, No. 1-3, 1998, pp. 249-262.
- Y. S. Zhang, Y. Q. Lu and S. Q. Pang, “Orthogonal Arrays Obtained by Orthogonal Decomposition of Projection Matrices,” Statistica Sinica, Vol. 9, No. 2, 1999, pp. 595-604.
- Y. S. Zhang, S. Q. Pang and Y. P. Wang, “Orthogonal Arrays Obtained by Generalized Hadamard Product,” Discrete Mathematics, Vol. 238, No. 1-3, 2001, pp. 151- 170. doi:10.1016/S0012-365X(00)00421-0
- Y. S. Zhang, L. Duan, Y. Q. Lu and Z. G. Zheng, “Construction of Generalized Hadamard Matrices D(rm(r + 1), rm(r + 1); p),” Journal of Statistical Planning and Inference, Vol. 104, No. 2, 2002, pp. 239-258. doi:10.1016/S0378-3758(01)00249-X
- Y. S. Zhang and S. S. Mao, “The Origin and Development Philosophy Theory of Statistics,” Statistical Research, Vol. 12, 2004, pp. 52-59.
- Y. S. Zhang, S. S. Mao, C. Z. Zhan and Z. G. Zheng, “Stable Structure of the Logic Model with Two Causal Effects,” Applied Probability and Statistics, Vol. 21, No. 4, 2005, pp. 366-374.
- N. Q. Feng, Y. H. Qiu, F. Wang, Y. S. Zhang and S. Q. Yin, “A Logic Analysis Model about Complex System’s Stability: Enlightenment from Nature,” Lecture Notes in Computer Science, Vol. 3644, 2005, pp. 828-838. doi:10.1007/11538059_86
- N. Q. Feng, Y. H. Qiu, Y. S. Zhang, F. Wang and Y. He, “A Intelligent Inference Model about Complex System’s Stability: Inspiration from Nature,” International Journal of Intelligent Technology, Vol. 1, 2005, pp. 1-6.
- N. Q. Feng, Y. H. Qiu, Y. S. Zhang, C. Z. Zhan and Z. G. Zheng, “A Logic Analysis Model of Stability of Complex System Based on Ecology,” Computer Science, Vol. 33, No. 7, 2006, pp. 213-216.
- Y. S. Zhang, “Data Analysis and Construction of Orthogonal Arrays,” East China Normal University, Shanghai, 2006.
- Y. S. Zhang, “Orthogonal Arrays Obtained by RepeatingColumn Difference Matrices,” Discrete Mathematics, Vol. 307, No. 2, 2007, pp. 246-261. doi:10.1016/j.disc.2006.06.029
- C. Y. Pan, X. P. Chen, Y. S. Zhang and S. S. Mao, “Logical Model of Five-Element Theory in Chinese Traditional Medicine,” Journal of Chinese Modern Traditional Chinese Medicine, Vol. 4, No. 3, 2008, pp. 193-196.
- X. P. Chen, W. J. Zhu, C. Y. Pan and Y. S. Zhang, “Multilateral System,” Chinese Journal of System Science, Vol. 17, No. 1, 2009, pp. 55-57.
- C. Luo and Y. S. Zhang, “Framework Definition and Partition Theorems Dealing with Complex Systems: One of the Series of New Thinking,” Journal of Shanghai Instituie of Thennolegy (Natural Science), Vol. 10, No. 2, 2010, pp. 109-114.
- C. Luo and Y. S. Zhang, “Framework and Orthogonal Arrays: The New Thinking of Dealing with Complex Systems Series Two,” Journal of Shanghai Institute of Technology (Natural Science), Vol. 10, No. 3, 2010, pp. 159- 163.
- X. D. Wang, Y. C. Tang, X. P. Chen and Y. S. Zhang, “Design of Experiment in Global Sensitivity Analysis Based on ANOVA High-Dimensional Model Representation,” Communications in Statistics: Simulation and Computation, Vol. 39, No. 6, 2010, pp. 1183-1195. doi:10.1080/03610918.2010.484122
- Research Center for Chinese and Foreign Celebrities and Developing Center of Chinese Culture Resources, “Chinese Philosophy Encyclopedia,” Shanghai People Press, Shanghai, 1994.
- J. Y. Liao, J. J. Zhang and Y. S. Zhang ,”Robust Parameter Design on Launching an Object to Goal,” Mathematics in Practice and Theory, Vol. 40, No. 24, 2010, pp 126-132
- C. Y. Pan; H. N. Ma; X. P. Chen and Y. S. Zhang, “Proof Procedure of Some Theories in Statistical Analysis of Global Symmetry,” Journal of East China Normal University (Natural Science), Vol. 142, No. 5, 2009, pp. 127- 137.
- X. Q. Zhang, Y. S. Zhang and S. S. Mao, “Statistical Analysis of 2-Level Orthogonal Satursted Designs: The Procedure of Searching Zero Effects,” Journal of East China Normal University (Natural Science), Vol. 24, No. 1, 2007, pp. 51-59.
- M.-J. Cheng, “Lao-Tzu, My Words Are Very Easy to Understand: Lectures on the Tao Teh Ching,” North Atlantic Books, Richmond, 1981.
- Lao-tzu, “Tao Te Ching,” 2010. http://acc6.its.brooklyn.cuny.edu
- Y. S. Zhang, W. G. Li, S. S. Mao and Z. G. Zheng, “Orthogonal Arrays Obtained by Generalized Difference Matrices with g Levels,” Science China Mathematics, Vol. 54, No. 1, 2011, pp. 133-143. doi:10.1007/s11425-010-4144-y
- J. T. Tian, Y. S. Zhang, Z. Q. Zhang, C. Y. Pan and Y. Y. Gan, “The Comparison and Application of Balanced Block Orthogonal Arrays and Orthogonal Arrays,” Journal of Mathematics in Practice and Theory, Vol. 39, No. 22, 2009, pp 59-67.
- C. Luo and C. Y. Pan, “Method of Exhaustion to Search Orthogonal Balanced Block Designs,” Chinese Journal of Applied Probability and Statistics, Vol. 27, No. 1, 2011, pp. 1-13.
- C. Luo, X. P. Chen and Y. S. Zhang, “The Turning Point Analysis of Finance Time Series,” Chinese Journal of Applied Probability and Statistics, Vol. 26, No. 4, 2010, pp. 437-442
- Y. S. Zhang, X. Q. Zhang and S. Y. Li “SAS Language Guide and Application,” Shanxi People’s Press, Shanxi, 2011.

