Journal of Information Security
Vol.5 No.3(2014), Article
ID:47297,10
pages
DOI:10.4236/jis.2014.53008
Encrypted CDMA Audio Network
Alfredo A. Ortega1, Víctor A. Bettachini1, Pablo I. Fierens1,2, José Ignacio Alvarez-Hamelin1,2
1ITBA (Instituto Tecnológico de Buenos Aires), Buenos Aires, Argentina
2CONICET (Consejo Nacional de Investigaciones Científicas y Técnicas), Buenos Aires, Argentina
Email: aortega@itba.edu.ar, vbettachini@itba.edu.ar, pfieren@itba.edu.ar, ihameli@itba.edu.ar
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 April 2014; revised 25 May 2014; accepted 20 June 2014
ABSTRACT
We present a secure LAN using sound as the physical layer for low speed applications. In particular, we show a real implementation of a point-to-point or point-to-multipoint secure acoustic network, having a short range, consuming a negligible amount of power, and requiring no specific hardware on mobile clients. The present acoustic network provides VPN-like private channels to multiple users sharing the same medium. It is based on Time-hopping CDMA, and makes use of an encrypted Bloom filter. An asymmetrical error-correction is used to supply data integrity, even in the presence of strong interference. Simulations and real experiments show its feasibility. We also provide some theoretical analysis on the principle of operation.
Keywords:Non-Audible Communication, Ad-Hoc Network, Security

1. Introduction
Information sharing and data synchronization among devices, such as mobile phones and computers, are frequently conducted through self-configurable ad-hoc wireless networks. For instance, networks based on IEEE 802.11 (Wi-Fi) or Bluetooth standards became ubiquitous due to, among other factors, their ease of use autonomous nature and independence of fixed structure. However, they are prone to security risks such as eavesdropping [1] -[3] or malicious manipulation of data [4] , as their RF traffic can be easily monitored from nearby locations.
In security-minded organizations, such as military, homeland security, R&D or even banks and other financial institutions, where it is imperative to restrict the flow of sensitive information to specific areas, it has become a necessity to find an alternative to RF communication for establishing ad-hoc networks. Non-RF wireless communication solutions resilient to out-of-room monitoring comprise free-space optical and acoustical links. A number of them are reviewed in [5] .
The main drawback of optical links is the requirement of a clear line of sight between devices, a condition that cannot be guaranteed in some working environments. Moreover, they require the installation of additional light sensing hardware on devices not equipped with cameras, or even infra-red transceivers.
Acoustical communications, however, can operate using standard hardware microphones and speakers, ubiquitous on information devices [6] . Furthermore, line of sight is not required to establish links among nodes which can be placed up to a meter apart, emitting low volume audio.
A similar technology addressing these user cases is RF based Near Field Communications (NFC) [7] , a wireless protocol which requires specialized hardware not currently present in most mobile devices. Unlike other technologies, e.g., optical fiber communications, the broadcast nature of sound waves makes privacy safeguards an essential requirement. Several audio communication systems have been proposed [8] . Acoustical communication is an excellent alternative to RF NFC [9] due to current availability of microphones and speakers. Additionally, inaudible ultrasonic or near ultrasonic communications assure that no disturbance is presented to people nearby the connecting nodes placed several meters apart [6] . Finally, there have been presented underwater acoustic protocols with ranges of more than 50 km are possible [10] .
But to the best of our knowledge, the question of privacy has been addressed only in the application layer using security protocols. We present a physical layer approach to secure acoustical communications based on time-hopping CDMA, similar to those presented in references [11] [12] . In this work, we present a pointto-point or point-to-multipoint secure acoustic network which has a short range and consumes a negligible amount of power, requiring no additional hardware on mobile clients.
Establishing a private link among previously un-paired mobile devices based on software privacy schemes requires some degree of user interaction that is usually neglected [5] . Since our proposal deals with privacy at the physical layer, user intervention is minimized.
An envisioned application scenario for this technology is the validation of small financial transactions such as PoS (Point of Sale) or ATMs using an unmodified mobile device (e.g. a smart phone).
2. Building a Secure Acoustical Network
The main advantage of the proposed system is its simplicity, just a sound emitter (speaker), a receiver (microphone) and a sound media channel are needed; and those are already available in computers, tablets and cellphones (Figure 1). Based on Secure Time-hopping CDMA, it provides unidirectional channels for point-topoint and multicast communications. Bi-directional communications can be established using two separates channels (i.e., two different CDMA codes in the same media), or by employing the same channel in half-duplex. The later proposition needs further developing work and falls beyond the scope of this paper. We provide further details in the following subsections.
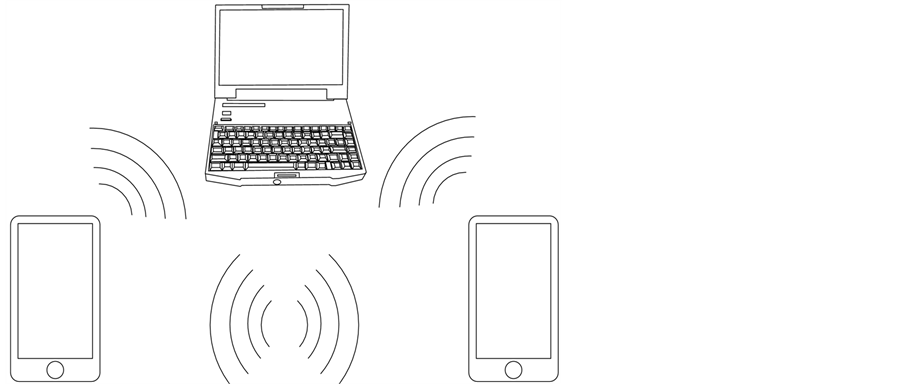
Figure 1. Proposed acoustic network may have heterogeneous nodes like cell-phones and personal computers.
2.1. Secure Time-Hopping CDMA
Code Division Multiple Access (CDMA) is usually implemented either as frequency hopping or direct-sequence spread-spectrum. However, we chose a time-hopping scheme because it enables a simple way of implementing a secure transmission and also to deal with broadcast media. Indeed, security is achieved, for each user communication, by selecting a time-slot to transmit each message bit, according to a cryptographically-secure pseudo-random number generator (CS-PRNG) [13] . Only the receivers having the appropriate CS-PRNG key can decrypt the transmission, thus allowing point-to-point and multicast communications. This is equivalent to a pre-shared key symmetrical encryption scheme, where credentials must be previously shared via a separate secure channel (as in all pre-shared key schemes). Being sound an inherently local-area physical media, keys can be shared verbally, in the same way Bluetooth (a similar protocol using radio-waves) PIN security works. It is important to remark that the security of the communication stack depends completely on the CS-PRNG algorithm and key length, and it is as strong as the algorithm selected for this component. Although no particular algorithm is specified for the implementation, but our simulations and implementation were done using ARC4 [14] for the CS-PRNG.
Communication channels are structured into frames with a certain number of slots/bits, where each user transmits data according to the CS-PRNG [13] . The seed of the CS-PRNG serves as a key shared by the sender and the receiver. Since pseudo-random sequences are non-orthogonal, collisions will occur between different channels (or users). Thus the system requires heavy use of Forward Error Correction (FEC, see [15] and references therein) to provide a required Bit Error Rates (BER) according to the capacity of the system. In this paper, we show that the use of FEC allows attaining a peak medium utilization of approximately 35%, close to that of the slotted-aloha protocol, a similar but non-secure transmission scheme [16] . A higher figure can be obtained using the same scheme with orthogonal codes, e.g., Gold codes instead of ARC4 for the CS-PRNG. However, the acoustic network would become insecure due to the predictability of such codes.
The size of the frame is proportional to the number of simultaneous users that the system supports. Increasing the frame size will cause the total bandwidth to be shared among more users, but transmission delay will also increase because the whole frame must be received to start decoding the data. Ideally frame size must be minimized.
2.2. Asymmetric Error Correction
Whenever On-Off Keying (OOK) modulation is used (see Section 2.4), the sound media can be modeled as a Z-channel [17] , i.e., a binary asymmetric channel in which the probability of erroneously decoding a transmitted 1 as a 0 is nil. This fact allows correcting errors using Bloom filters [18] . In its simplest form, each user transmits K copies of each data bit. Since the position of each copy in the frame is determined by the local CS-PRNG, communication is encrypted. In a Z-channel, transmitted 0 s can only be overridden by collisions with 1 s transmitted by other users; so even in the presence of a collision, redundancy reduces the probability of error. That is, if at least one 0 is detected among the K copies, then there is certainty that a 0 was transmitted. Decoding becomes a simple task which only involves the binary-AND of the K received bits1 (see Figure 2). The complete error correction scheme follows a standard inner-outer code architecture. While for the inner code we use a Bloom filter, the outer code is a regular Reed-Solomon 223/255 code.

Figure 2. Symbol insertion into the Bloom filter, considering symbols with two 1 s and length or redundancy of 3. Arrows indicate assigned slot by the CS-PRNG.
2.3. Hamming Weight Equalization
As an enhancement of the Bloom filter stage, Hamming weight equalization can be implemented as follows. Each user parses its output stream in groups of n bits and maps them to words of m bits with exactly m1 1 s. Notice that encoding has multiple 0 s, and due to the Z-channel property, they do not interfere with other users transmissions in the physical media. Such proposed mapping is possible if the combinatorial number of subsets of m1 elements taken out of a set of size m is at least 2n, i.e.
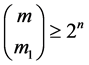 , (1)
, (1)
notice that there is space for error detection in the case of a strict inequality. Furthermore, the reduction of Hamming weight from an average of n/2 to a fixed m1/m has two effects:
1) Optimization of the Bloom filter algorithm, as low Hamming weight symbols lead to a reduced collision rate;
2) Since all symbols have the same Hamming weight, no information can be extracted from the statistical analysis of the number of 1 s and 0 s.
The encoding/decoding process can be accomplished by using a simple lookup table, so it has O(1) time complexity, but O(m2) space complexity. A frame encoded using words of weight m1 will have W1 = m1 ´ N ´ K bits in the 1 state, where N is the number of clients/encrypted channels and K is the Bloom Filter repetition parameter (see Figure 2). It is clear that the frame length M has to be at least W1 long. As M increases, the probability of collision and, hence, the probability of error decreases. However, spectral efficiency also decreases, so the final users’ channel capacity.
2.4. Modulation and Synchronization
On-off keying modulation of sound waves, following the Z-channel interface model described in Section 2.2., encode transmitted bits as pulses. Carrier frequency can vary from 10 kHz to 16 kHz. Good results can be obtained with a rate of 1000 bps at frame level. In experiments, delay (the time for a bit to traverse the network) was very high, due to Reed-Solomon 223/255 coding, a frame to support up to 16 users and the low capacity of the physical media. A more sensible choice of FEC algorithm (like BCH [15] ) could drastically reduce data delay. Simple pulse shaping is realized using a pass-band filter at the output of the modulation and also at the input of the demodulator. This filter also helps reject unwanted interference.
As it follows from the description of the communication channel, synchronization between transmitter and receiver is essential for the correct decoding of information. For this purpose, an initial synchronization pattern is sent, so the receiver can adjust parameters like phase and decision level (see Figure 3). An enhanced detection was observed in our experiments when a duty cycle of 50% was used for data bit transmission. Clock drift and jitter are not significant at this low transmission speed and so no correction is required, making the software modem implementation very simple. Decision level is dynamic, i.e., it is constantly re-calculated from averaged input data. Receiver symbol phase is also corrected using the input data as reference. Notice that this simple synchronization method allows detecting the frame start as well as the bit slot; both are needed at every communication. Moreover, once the data began to be transmitted, the communication becomes indecipherable thanks to the CS-PRNG.

Figure 3. (a) The synchronization pattern is a OOK (ASK) modulation of a 1-0-1-0 sound pattern. It is shown here before pulse shaping; (b) Once synchronization is done, the actual data bits are transmitted with the same modulation but with a duty cycle of 50%.
3. Probability of Collision for a Z-Channel
In this section, we present an analytical estimate of the upper bound of the bit error probability, taking into account only the interference from other users in the network. Moreover, we will not consider the correction capability of the Reed-Solomon code.
As explained in Section 2.3, let us assume that each user groups information bits into packets of length n. Each packet is coded using exactly m1 ones and m0 zeroes (m1 + m0 = m). Each of the resulting m binary digits is repeated K (Bloom filter length) times at randomly chosen places in a frame of length M. Repetitions of a binary digit may collide with other repetitions of the same digit or with those corresponding to another digit. Let N be the number of active users.
In order to roughly estimate the bit error rate, we shall make the following simplifying assumptions:
We shall assume that frames from different users are synchronized and, thus, each frame contains (counting collisions) W0 = N ´ K ´ m0 zeroes and W1 = N ´ K ´ m1 ones.
We shall not include in the analysis the possibility of error correction due to the fact that, in general,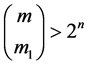 .
.
More specifically, whenever an erroneous sequence of m binary digits with more than m1 1 s is received, it is mapped to a randomly selected bit string of length n. Therefore, the expected number of errors will be n/2.
Under these assumptions, the bit error rate for a given user is given by
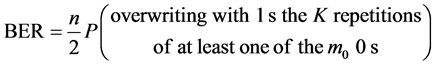 , (2)
, (2)
By the union bound,
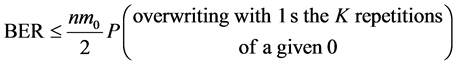 , (3)
, (3)
Thus, let us fix our attention on one of the m0 zeroes. If the transmitted (by all users) W1 ones occupy s slots and the K repetitions of the given 0 use r (≤ K) slots, then a necessary condition for error is that s ≥ r. So let us assume that there are s 1 s in a frame of M bits. Given r (fixed) places in the frame, the probability that the 1 s occupy those r positions is given by
 (4)
(4)
where we have assumed that M, s >> r.
If M >> K, it is not difficult to see that the K repetitions of a given 0 occupy µR ≈ K slots in average. It can also be shown that the average number of slots occupied by the W1 1 s transmitted by all users is
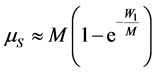 , (5)
, (5)
if M and W1 are large (see Appendix).
From these equations, a rough estimate of the bit error rate for a given user is
 . (6)
. (6)
Figure 4 shows an upper bound of BER as a function of K for M = 256, m0 = 22, m1 = 2 and n = 8 for N = 8 simultaneous clients. It is interesting to note that there is an optimal value of the repetition rate K which minimizes the bit error rate. This result, is of relevance in the design of a given communication system. In particular, this last equation is very simple and may aid network design. Notice that the lowest BER attained allows Reed-Solomon algorithm to make further corrections, yielding to a channel with a BER around of 10−4 (e.g., Figure 6), sufficient for applications targeted in this work.

Figure 4. BER estimate vs. Bloom filter repetition rate. ReedSolomon coding is not taken into account. The theoretical calculations are an upper bound for the BER. At K = 11 the lowest bound is found. Not only its shape is quite similar to the BER found through numerical simulations, but also the actual minimum BER is found for K = 10, very close to that indicated by the theoretical calculation. Results shown are for a frame of M = 256 assuming 8 simultaneous clients.
4. Numerical Simulations
In order to study the behavior of our protocol, we developed a piece of software implementing the present proposal. We detail firstly, the software architecture, and secondly the results of the performed simulations.
4.1. Simulation Software
In order to match the communication stack accurately, we adopted a modular software architecture where the modules are chained via POSIX standard input/outputs. This structure allows to modify each stage separately and to reuse some of the simulations’ modules at the final implementation without modification. The high-level structure can be seen at Figure 5. All modules of the software simulator are available under an open GPL license [11] .
Each simulation run begins when a binary data block (random bit sequence) is fed to the first module, that is, the Reed-Solomon encoder. The output of this encoder is fed to the next block, an interleaver. In this way, the original data is transformed at each stage and successively passes through all modules until it is converted into audio. At the receiver stage the demodulator generates the binary data blocks that go in reverse order through the same modules of the modulator stage, until the receiver Reed-Solomon decoder is reached. At this stage, the system compares the original input with the output, and calculates and reports the BER.
In the numerical simulations, no noise was added to the audio channel, but speaker and microphone hardware limitations were simulated using bandpass filters at the carrier frequency with a 4 kHz bandwidth. Filters were implemented using the Sound eXchange (SoX) Unix utility.
Normally over 106 bits need to be simulated for each client under this configuration. Computational resources needed for simulation are considerable, so the software provides a client-server model in which calculations can be shared among multiple nodes.
4.2. Simulation Results
Simulations show a peak medium utilization of 35% (consistent with a slotted-aloha type network [16] ) when the maximum of 12 encrypted channels are in use. This maximum amount of channels correspond to a system with frame length M = 256, Bloom filter length K = 9, symbol length is n = 8 bits and Hamming weight of all transmission symbols set at m1 = 2. Note that with a fixed Hamming weight of 2, random input symbols of 8-bit length are converted to input symbols of length m = 24. The amount of data transferred to measure each data point was 1 M bit.
It is important to note that only a client-to-client interference was simulated with no ambient noise. The OOK modulation is more sensitive to noise than other more efficient modulation schemes, but the flexibility of the
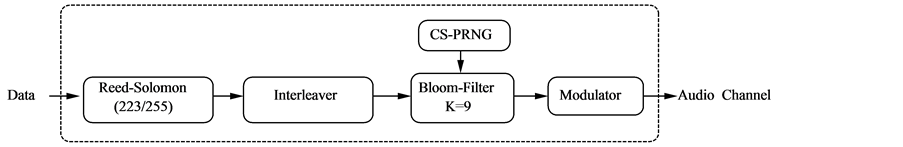
Figure 5. Software stack of the modulator stage.
error correction architecture adapts to situations of high ambient noise by simply reducing the amount of available encrypted channels, as we will discuss in the next section.
Simulation results tracked closely that of experiments with the physical implementation of the scheme (see Figure 6). Very low BER values were not detected because not enough data was collected in the simulation, just 1 Mbit of data per user.
5. Experimental Results
We present here the results of real world scenarios, testing our protocol in two computers Lenovo T420 and Lenovo X60, and one cell-phone HTC Status. We developed a version working on GNU/Linux and another on Android.
All measurements were conducted at a rate of 1000 bps at the physical media, with a 16 kHz carrier signal, while maintaining the other parameters in the same values that were used in the simulations, including the bandpass filter centered at 16 kHz with a 4 kHz width. The transmitted data was 4096 bits per user, with M = 256. This M, lower than the simulated cases, was used due it reduces the delay before the end user starts to receive information, which is introduced by the error correction. Indeed the implemented Reed-Solomon needs 256 bytes blocks to perform corrections. Sound output volume was set at the maximum possible for each device, while the sound input amplification was optimized for each measurement.
Figure 6 shows the comparison between simulations and experimental results in a real scenario between two laptops separated 25 cm. It can be observed that even for a high number of concurrent clients (e.g., up to 10 simultaneous users) the system does not exhibit a high error rate; the BER is less than 10−4, for both, simulated and real systems. As the proposed system is designed for low capacity, this BER is acceptable.
We also performed an experiment to test the BER as a function of distance, using a cell-phone as a transmitter and the computer as a receptor. Figure 7 shows that the system works in distances below 1 m (notice that it will need an additional error correction between 50 cm and 1 m). Below 50 cm there is no detectable error in our measurements.
We performed experiments with the system operating at different carrier frequencies; we discuss them in the following paragraphs.
Communications using a 12 kHz tone carrier were extremely susceptible to ambient noise. Indeed, a 50 cm link between a laptop Lenovo T420 and a HTC Status phone suffered an excess of 15% BER with slight noise interference (like little bumps on a nearby table). This observation motivated the use of the highest attainable frequency. A 16 kHz carrier provided the widest range of compatibility among tested devices, because some of them could not emit at higher frequencies.
Tests were also done at the highest frequencies attainable for each device. For instance, laptop speakers in Lenovo T420 and Lenovo ×60 laptops proved capable of establishing a link at 19.2 kHz, but only for very short distances (20 cm). Nevertheless, this carrier frequency allowed a faster link (2000 bps) with the same BER.
The modulated sound signal can represent a nuisance to nearby persons and animals. Several different carrier frequencies were tested as a way to evaluate the level of discomfort. The 19.2 kHz carrier signal was perceived as almost non-audible, with 16 kHz being clearly audible for most people and the link at 12 kHz being the most uncomfortable. It should be noticed that loudness and hence discomfort increase with the number of simultaneous users.
6. Conclusions
We presented a wireless secure communication protocol that uses sound waves as the transmission physical media. It can be used as a point-to-point or point-to-multipoint protocol as digital data can be transmitted using dif-

Figure 6. Link between two laptops (Lenovo T420 and Lenovo ×60) simulating multiple client nodes. No errors were measured for 10 to 14 clients when transmitting 4096 bits.

Figure 7. Link between Laptop (Lenovo T420) and Mobile Phone (HTC Status) presents errors only over 60 cm. At a 50 cm separation, and below, no errors were recorded with 4096 transmitted bits.
ferent carrier frequencies. More importantly, the protocol can use transducers and sensors like speakers and microphones already present in billions of devices like desktops, laptops and other mobile computers.
Security is built-in into the system, guaranteed by Time-Hopping CDMA with a CS-PRNG. Design problems, like the delay before communication starts and limited available bandwidth in standard audio channels, can be easily corrected by adjustments to system parameters. For instance, a mechanism for dynamic utilization and assignation of the channels as a function of the present users (i.e., noise), can be implemented to improve the capacity of the system. Although in the present test channel the mentioned delay was excessive (66 s) for some applications requiring short response times (e.g. banking transactions), this can be reduced by decreasing the maximum number of simultaneous users supported by the system, and implementing both a lower-delay interleaver and an outer error correction algorithm like BCH.
We validate our proposition by simulations, theoretical analysis and experiments in real scenarios. Our protocol may provide an economical alternative to NFC, RFID, two-factor authentication, ATM-banking or any other application requiring cryptographically secure network access at short distances.
Acknowledgements
This work was supported by PICT-497/2006 of the Agencia Nacional de Promoción Científica y Tecnológica (ANPCyT), Argentina.
References
- Zhang, F., He, W., Liu, X. and Bridges, P.G. (2011) Inferring Users’ Online Activities through Traffic Analysis. WiSec’11—Proceedings of the 4th ACM Conference on Wireless Network Security, Hamburg, 15-17 June 2011, 59-69. http://dx.doi.org/10.1145/1998412.1998425
- Mathur, S., Trappe, W., Mandayam, N., Ye, C. and Reznik, A. (2008) Radio-Telepathy: Extracting a Secret Key from an Unauthenticated Wireless Channel. MobiCom 2008—Proceedings of the 14th ACM International Conference on Mobile Computing and Networking, San Francisco, 14-19 September 2008, 128-139. http://dx.doi.org/10.1145/1409944.1409960
- Jakobsson, M. and Wetzel, S. (2001) Security Weaknesses in Bluetooth. In: Naccache, D., Ed., Topis in Cryptology— CT-RSA 2001, Springer, Berlin Heidelberg, 176-191. http://dx.doi.org/10.1007/3-540-45353-9_14
- Radosavac, S., Cárdenas, A.A., Baras, J.S. and Moustakides, G.V. (2007) Detecting IEEE 802.11 MAC Layer Misbehavior in Ad Hoc Networks: Robust Strategies against Individual and Colluding Attackers. Journal of Computer Security, 15, 103-128.
- Kumar, A., Saxena, N., Tsudik, G. and Uzun, E. (2009) A Comparative Study of Secure Device Pairing Methods. Pervasive and Mobile Computing, 5, 734-749. http://dx.doi.org/10.1016/j.pmcj.2009.07.008
- Hanspach, M. and Goetz, M. (2013) On Covert Acoustical Mesh Networks in Air. Journal of Communications, 8, 758-767. http://dx.doi.org/10.12720/jcm.8.11.758-767
- ECMA International (2005) Near Field Communication—White Paper. http://www.ecma-international.org/activities/Communications/tc32-tg19-2005-012.pdf
- August, K.G., Sizer II, T. and Wright, G.A. (2000) Apparatus and Method for Initiating a Transaction Having Acoustic Data Receiver That Filters Human Voice. US Patent No. 6125172.
- Nandakumar, R., Chintalapudi, K.K., Padmanabhan, V. and Venkatesan, R. (2013) Dhwani: Secure Peer-to-Peer Acoustic NFC. ACM SIGCOMM 2013—Proceedings of the Conference of the ACM Special Interest Group on Data Communication, Hong Kong, 12-16 August 2013, 63-74. http://dx.doi.org/10.1145/2486001.2486037
- Leus, G., Van Walree, P., Boschma, J., Fanciullacci, C., Gerritsen, H. and Tusoni, P. (2008) Covert Underwater Communications with Multiband OFDM. OCEANS 2008, Oceans, Poles and Climate: Technological Challenges, Quebec, 15-18 September 2008, 1-8. http://dx.doi.org/10.1109/OCEANS.2008.5151860
- Ortega, A.A., Bettachini, V.A., Grosz, D.F. and Alvarez-Hamelin, J.I. (2011) Point-to-Point and Point-to-Multipoint CDMA Access Network with Enhanced Security. Advanced Photonics, OSA Technical Digest (CD), Toronto, 12-14 June 2011, Paper ATuB6. http://dx.doi.org:10.1364/ANIC.2011.ATuB6
- Ortega, A.A., Bettachini, V.A., Grosz, D.F. and Alvarez-Hamelin, J.I. (2012) Hamming-Weight Minimisation Coding for CDMA Optical Access Networks with Enhanced Security. International Conference on Future Generation Communication Technology (FGCT), London, 12-14 December 2012, 185-189. http://dx.doi.org/10.1109/FGCT.2012.6476559
- Menezes, A.J., van Oorschot, P.C. and Vanstone, S.A. (1996) Handbook of Applied Cryptography. CRC Press, Boca Raton. http://dx.doi.org/10.1201/9781439821916
- Harris, B. (2006) Improved Arcfour Modes for the Secure Shell (SSH) Transport Layer Protocol. http://www.rfc-base.org/rfc-4345.html
- Moon, T.K. (2005) Error Correction Coding: Mathematical Methods and Algorithms. John Wiley & Sons, New York. http://dx.doi.org/10.1002/0471739219
- Roberts, L.G. (1975) ALOHA Packet System with and without Slots and Capture. Computer Communication Review, 5, 28-42. http://dx.doi.org/10.1145/1024916.1024920
- Tallini, L.G., Al-Bassam, S. and Bose, B. (2002) On the Capacity and Codes for the z-Channel. Proceedings of the IEEE International Symposium on Information Theory (ISIT’02), Lausanne, 30 June-5 July 2002, 422. http://dx.doi.org/10.1109/ISIT.2002.1023694
- Bloom, B.H. (1970) Space/Time Trade-Offs in Hash Coding with Allowable Errors. Communications of the ACM, 13, 422-426. http://dx.doi.org/10.1145/362686.362692
Appendix: Proof of the Results in Section 3
Let us fix our attention on one of the m0 0 s sent by a user. The probability that exactly r of the M slots in the frame are used by the K repetitions of that 0 is given by
 . (7)
. (7)
If M and K are large, we get
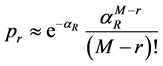 , (8)
, (8)
where , i.e., the distribution of the number of slots which are not occupied by the repetitions of a given 0 is approximately Poisson with mean
, i.e., the distribution of the number of slots which are not occupied by the repetitions of a given 0 is approximately Poisson with mean . If M >> K, then the average of such number of unoccupied slots is,
. If M >> K, then the average of such number of unoccupied slots is, . Thus, the number of slots occupied by the K repetitions of a given 0 is
. Thus, the number of slots occupied by the K repetitions of a given 0 is .
.
In a similar manner, the probability that exactly s of the M slots in the frame are occupied by the W1 1 s (sent by all users) is given by
 . (9)
. (9)
If M and K are large, we get
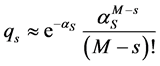 , (10)
, (10)
where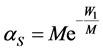 , i.e., the distribution of the number of slots which are not occupied by the repetitions of all 1 s of all users is approximately Poisson with mean
, i.e., the distribution of the number of slots which are not occupied by the repetitions of all 1 s of all users is approximately Poisson with mean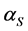 . Then the average of the number of occupied slots is
. Then the average of the number of occupied slots is
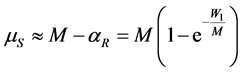 . (11)
. (11)
NOTES

1More efficient soft-decoding is also possible.

