Journal of Information Security
Vol.5 No.1(2014), Article ID:41815,11 pages DOI:10.4236/jis.2014.51001
Investigating Approaches of Data Integrity Preservation for Secure Data Aggregation in Wireless Sensor Networks
1Department of Computer Engineering, C. K. Pithawalla College of Engineering and Technology, Surat, India
2S. V. National Institute of Technology, Ichchanath, Surat, India
3Department of Electronics and Information Technology, Ministry of Communications and Information Technology, India
Email: vivakshajariwala@gmail.com
Received November 21, 2013; revised December 18, 2013; accepted December 26, 2013
ABSTRACT
Wireless Sensor Networks (WSNs) typically use in-network processing to reduce the communication overhead. Due to the fusion of data items sourced at different nodes into a single one during in-network processing, the sanctity of the aggregated data needs to be ensured. Especially, the data integrity of the aggregated result is critical as any malicious update to it can jeopardize not one, but many sensor readings. In this paper, we analyse three different approaches to providing integrity support for SDA in WSNs. The first one is traditional MAC, in which each leaf node and intermediate node share a key with parent (symmetric key). The second is aggregate MAC (AMAC), in which a base station shares a unique key with all the other sensor nodes. The third is homomorphic MAC (Homo MAC) that is purely symmetric key-based approach. These approaches exhibit diverse trade-off in resource consumption and security assumptions. Adding together to that, we also propose a probabilistic and improved variant of homomorphic MAC that improves the security strength for secure data aggregation in WSNs. We carry out simulations in TinyOS environment to experimentally evaluate the impact of each of these on the resource consumption in WSNs.
Keywords:In-Network Processing; Integrity; Message Authentication Code; Secure Data Aggregation; Wireless Sensor Networks
1. Introduction
Wireless sensor networks (WSNs) have gained significant attention in recent years. Sensor networks are used in a variety of applications such as environmental monitoring, military applications, surveillance, healthcare, home automation, control system in industry [1] etc. WSNs are composed of a collection of resource restricted tiny sensor nodes with limited battery power, storage, communication and computational capabilities [1]. As a general architecture, sensor nodes sense the specified physical parameter and route the data value sensed to a base station for further analysis. Often the sensed information contains correlated and redundant data. Hence, it is inefficient for all nodes of network to transmit sensed data to the base station. By the fact that sensor nodes have limited computation power that consumes less energy than radio operations, there is scope for in-network data processing. In in-network processing of data, each sensor node senses the required measurements and sends the data value to another node up in the hierarchy called the aggregator node [2]. The aggregator node collects measurements from different sensor nodes using which it generates a single representational aggregated value by applying an aggregate function. Subsequently, instead of sending all the messages towards the base station, the aggregator transmits only one aggregated result towards the base station [3].
However, with such a paradigm, any malicious update to the aggregated value can render numerous other sensor readings from various nodes also invalid. Even otherwise, the WSNs being deployed in hostile environments, various kinds of attacks are possible including attacks from outsider adversaries and compromised and previously legitimate nodes [4]. Thus, protocols for WSNs should be designed to prevent malicious inside nodes from damaging the whole network’s functionality or at least constrain their impacts on a reasonable level.
Amongst various security attributes in WSNs, we focus this discussion on data integrity. The approaches to providing data integrity can be either cryptography-based or non-cryptography-based. Our focus here is only on cryptographic approaches. As per our literature survey, we categorize the techniques for supporting data integrity in Secure Data Aggregation into three classes viz. Signature based, Hash function based and Message Authentication Code (MAC) based [5]. The digital signature based approach yields non-repudiation property, however, entails higher overhead as compared to other approaches. To counter the overhead due to the digital signature, our focus here is on the message authentication code based integrity support for secure data aggregation in WSNs.
In this paper, we analyze three cryptographic based approaches to supporting integrity. Our first approach is based on traditional MAC based integrity. In this approach, each leaf node shares its secret key with its parent node. Each leaf node generates MAC of the message with key shared with its parent and sends it to its immediate parent. After receiving message and MAC from the child, the parent checks for the sanctity of the MAC.
Our second approach is based on aggregate message authentication code (AMAC) [6]. The scheme with aggregate MAC allows the base station to share a distinct key with every other node in the WSNs. In this scheme, each node generates a tag of MAC and transmits it to its immediate parent node. The parent node receives tag from all the child nodes, computes aggregate tag on that and transmits it to the Base Station (BS). Finally, the base station verifies the integrity of all the nodes of the network.
Our third approach is based on homomorphic MAC (Homo MAC). Homo MAC [7] is a purely symmetric approach, and is the most computationand communication-efficient, but requires all data collecting nodes to share one global key with the base station. The security of Homo MAC scheme is based on a pseudo random generator. Thus, one of the obvious limitation of the basic Homo MAC is that if the cryptosystem encounters the same random number (as was used in a previous run), to generate two different tags, the adversary can know the key and generate a false tag. To improve intrinsic strength of Homo MAC, we also propose a solution that uses the set membership data structure viz. bloom filter to avoid repetition of a random number used in generation of tag of Homo MAC. The only argument against the usage of the proposed variant could be that if at all we have a strong random number generator that ensures nonrepetition, is it necessary to employ this variant? However, in that case, Homo MAC remains dependent on the implementation to be secure—the algorithm lacks intrinsic security strength. Hence, our proposal is justified in enhancing the intrinsic security strength of the homo MAC without assuming any guarantees from the underlying implementation. Our results clearly show that our variant of Homo MAC is suitable for any application demanding integrity support including secure data aggregation in resource constrained environment of WSNs.
The rest of the paper is as follows. In Section 2, we describe related work. In Section 3, we discuss Security Prerequisite and Network Environment. In Section 4, we present our proposed MAC based integrity support for SDA. In Section 5, we discuss AMAC based integrity support for SDA. Homo MAC based integrity support and our variant of Homo MAC are there in Section 6. Section 7 contains implementation details and simulation results. In Section 8, we present concluding remarks followed by references.
2. Related Work
Hu L. & D. Evans [8] proposed protocol named secure aggregation for wireless networks. It was based on the concept of delayed verification. At each round r, each leaf node of the tree sends its measurement reading and a message authentication code using the round key using μTesla. Round key is derived with the secret key shared with the base station. Data is aggregated as it propagates towards the base station. After receiving all final aggregation results, the base station starts the verification process. It reveals nodes’ keys to the entire network. This revelation of keys enables each node to verify data integrity and authenticity of the data. Authors in [9] extended the scheme of [8] by all two nodes in the two-hop communication range sharing pair-wise keys and then the scheme eliminates the usage of μTESLA, the fact that both schemes are only capable of preventing a single inside malicious node at an appreciable communication cost makes them impractical.
Yang, Y. et al. [10] came up with protocol named SDAP. Probability based grouping is done for tree nodes and in this group leader for node is selected. Default leader will be the base station. Leaf node sends data to the parent with the MAC. The intermediate node saves data received from the child and generates new aggregate value and signature. A signature is generated to represent the commitment hash tree. The group leader node sends final aggregate to the base station. It uses commitment hash that is similar to merkle hash tree for integrity check. Merkle tree is binary tree but schema used in this paper allows any number of child nodes. Verification uses Grubbs’ test to select a branch for integrity check.
Rodhe, I. et al. [11] came up with protocol named n-LDA. Aggregation tree is divided into layers. The layer closest to the base station is layer 1. Nodes near to layer 1 are layer 2 and so on. Each layer i have key Ki shared by all node in that layer. Key Ki is also known to (i − n)th layer. The base station knows all Ki where I <= n. Nodes have also shared a key with the next hop on route towards the base station. Encryption is done by adding the layer key and the hop-by-hop key. Each node also sends a list L of size n − 1 that shows number of nodes contributed in aggregation from n − 1 layer and next to it. Decryption is done by subtracting hop-by-hop key and subtracting all keys from nth layer next to the node. Hence, it is layered encryption. n-layer of encryption protects the data in intermediate transmission after n-hop is traversed. After initial n-layers are travelled by the data, one layer of encryption is removed and one new layer of encryption is added.
Przydatek, Song, and Perrig [12] proposed secure information aggregation (SIA) to identify forged aggregation values from malicious nodes. In the SIA scheme, a special node named aggregator computes an aggregation result over raw data together with a commitment to the data based on a Merkle-hash tree and sends them back to a remote user, which later challenges the aggregator to verify the aggregation.
Bagaa M. et al. in [13] introduced a new protocol named SEDAN. This protocol overcomes the scalability issue of [8]. The limitation is defeated by introducing new types of key that is shared between one-hop and two-hop neighbours. This eliminates the need of broadcasting of round keys for all nodes. This protocol removes delayed verification and integrity of data can be checked immediately with pre-shared keys. Thus, all aggregation results arriving at the base station are correct and can be committed immediately. This eliminates explicit verification phase that notably reduces the data transmission.
In this paper, we investigate approaches (MAC based, aggregate MAC based and homormophic MAC based) for preserving integrity for secure data aggregation in WSNs. In addition to that, we also propose our own variant of homomorphic MAC for preserving integrity for secure data aggregation in WSNs.
3. Security Prerequisite and Network Environment
For our research, we selected wireless sensor network that consists of N number of sensor nodes that are sensitive of energy consumption, having less memory and less computational resources [1]. Base station is concerned about results generated from the network. Consequently, we assume data aggregation mechanism is there in wireless sensor network.
There are basically three types of nodes in sensor network.
a) Leaf node that collects data from surrounding environment, generates messages, and transfers those messages to the higher-level node.
b) Aggregator node that collects the messages generated by the leaf node, then applies aggregation function on messages. Aggregator nodes may add their own data to the aggregation function.
c) Base station that receives the final aggregate value of the whole network, also verifies the integrity of the received messages. Aggregator node can also verify the integrity of message if application demands hop-by-hop verification of the messages.
The data are aggregated through the wireless sensor networks and base station retrieves aggregated results. To produce average of the data, base station will retrieve the sum of all messages of the network and the total number of nodes involve in aggregation. For the sake of ease, we assume that our WSNs are organized in a tree topology rooted at the base station. However, our proposed schemes fit into any kind of architecture including cluster. The basic objective of our proposals is to provide the message integrity for secure data aggregation in a cryptographic way; hence, a tag generated from any authentication function shall append to a message. However, we can easily incorporate privacy and confidentiality to our proposed approach of integrity using any benchmarked algorithms of [14] to make secure data aggregation versatile. In this paper, we are not focusing on the issues of key management and aggregation tree construction.
4. Message Authentication Code Based Integrity Support for Secure Data Aggregation
In this section, we discuss MAC based hop-by-hop integrity support for secure data aggregation in WSNs. In hop-by-hop integrity, if malicious adversary has inserted any false data in the networks that will be detected immediately at next hop. Therefore, that malicious data do not travel towards the base station. In contrast to that, in end-to-end integrity, false data will be detected only at the end i.e. at the base station, wasting energy and lifetime of sensor networks. Thus, our proposed approach of hop-by-hop integrity in secure data aggregation can save bandwidth of the sensor networks and increase the lifetime as well as security of sensor nodes.
In our approach of hop-by-hop MAC based integrity, each leaf node shares secret key with parent and each leaf node generates MAC using SHA-1 on the outgoing message with the help of the shared key. Similarly, after receiving the message and computed MAC from child, aggregator node or Base station will again compute MAC with the key shared with child and verify the integrity of the message. For example, in our approach, node 3 generates MAC on data of node 3 so M3 (MAC 3) is generated that is received by node 1. Similarly node 4 generate MAC on data of node 4 so M4 (MAC 4) is generated that is also received by node 1. Now node 1 have M3 (MAC 3) and M4 (MAC 4), so node 1 verify M3 and M4. If it is verified, then only node 1 will accept message from node 3 and 4 and apply aggregation function on it and generate m1. Otherwise, node 1 will not accept the messages from node 3 and node 4 and simply discard the messages. If node 1 has accepted messages from node 3 and node 4 and generated aggregated message, node 1 apply MAC on aggregated message and generate M1 (MAC 1). Same way node 0 (Base station) accept messages from node 1 and node 2 only if M1 (MAC 1) and M2 (MAC 2) is verified.
In our proposed approach of secure data aggregation algorithm 1 is to be implemented on the leaf node. In this, each sensor node computes Mi on the outgoing message mi.
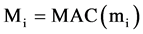
Parent of sensor node receives Mi and mi and parent compute Mi on received mi. If received Mi is same as computed Mi, parents accept the message and apply aggregation on message. After aggregation, parents compute MAC on aggregated message and send it further. (Figure 1).
Leaf Node
// Each leaf node will computes following MAC Generation: Each sensor computes Mi= MAC(mi)
Append this Mi to message and send it to parent node
Algorithm 2: Aggregator Node and Base Station
// Aggregator Node and Base station will computes following Verification of MAC:
Aggregator or Base station received Mi and mi
Compute Mi= MAC(mi)
Verify Computed Mi = received Mi
Base station can get m = ∑ mi
Algorithm 2 is to be implemented on the aggregator node and base station. Aggregator node or Base station will receive aggregated message and MAC of sensor nodes. Aggregator node or Base station again compute MAC of the received message and verify that weather received MAC is same as computed MAC or not. Thus, our approach ensures hop-by-hop integrity through MAC.
5. Aggregate Message Authentication Code (AMAC) Based Integrity Support for Secure Data Aggregation
Aggregate MAC (AMAC) [6] takes multiple MAC tags generated by different leaf nodes, aggregate those different MAC tags and generate single tag. This generated single tag can be verified either by aggregator nodes or by the base station. Aggregate MAC is provably secure [6] and can be constructed from any standard message authentication code like CBC-MAC [15], HMAC [16], block cipher mode of operations [17] or any hash functions. Let ki be the symmetric key shared by node i and the base station. MAC be a standard deterministic MAC. To authenticate a message mi, node i generates a tag: ti = MACki (mi). Any aggregator can aggregate j tags by simply computing the XOR of all the tag values:
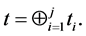
Then the base station uses the aggregate tag t to verify the authenticity of all raw messages by checking whether 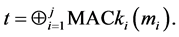
An aggregate message authentication code is a tuple of probabilistic polynomial-time algorithms (MAC, Agg, Vrfy) such that [6]:
1) Authentication algorithm MAC: upon input a key k Є {0,1}n and a message m Є {0,1}n, algorithm MAC outputs a tag tag. We denote this procedure by tag = MACk(m).
2) Aggregation algorithm Agg: upon input two sets of message/identifier pairs 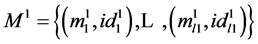 ,
, 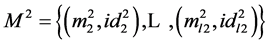 and associated tags
and associated tags
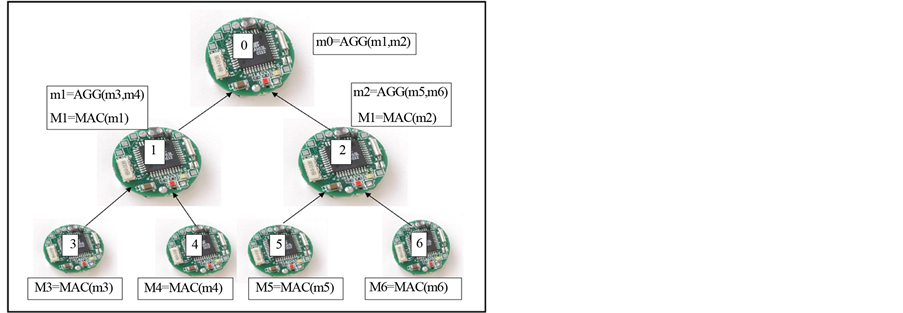
Figure 1. MAC based hop-by-hop integrity support.
tag1, tag2 algorithm Agg outputs a new tag. This algorithm is unkeyed.
3) Verification algorithm Vrfy: upon receiving a set of key/identifier pairs {(k1,id1), ×××, (kt; idt)}, a set of message/identifier pairs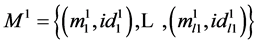 and a tag tag, algorithm Vrfy outputs a single bit, with “1” denoting acceptance and “0” denoting rejection. We denote this procedure by Vrfy(k1,id1), ×××, (kn;idt)(M,tag).
and a tag tag, algorithm Vrfy outputs a single bit, with “1” denoting acceptance and “0” denoting rejection. We denote this procedure by Vrfy(k1,id1), ×××, (kn;idt)(M,tag).
In this integrity preserving approach of secure data aggregation, algorithm 1 is to be implemented on the leaf node. In this, each sensor node computes tagi on the outgoing message mi.

Parent of sensor node receives tagi from ith leaf node and tagj from jth leaf node. Aggregator node then compute tag on received Mi and Mj as tag = tagi ⊕ tagj and transmit this tag to the base station.
Algorithm 1: Leaf Node
// Each leaf node will computes following tag Generation: Each sensor computes tagi= MACki(mi)
Append this tagi to message and send it to parent node
Algorithm 2: Aggregator Node
// Aggregator Node will computes following Aggregate tag generation:
Aggregator Node receives tagi and tagj from ith and jth leaf node Compute tag = tagi⊕tagj
Transmit tag to Base Station Algorithm 2 is to be implemented on the aggregator node. Aggregator node will receive tag generated by each leaf nodes. Aggregator node then applies ⊕ operation on all the received tag, generates combined tag and sends this combined tag to the base station.
Algorithm 3: Base Station
// Base Station will computes following Verification of tag:
Base station received tag generated by Aggregator Node Verify the tag with key shared with leaf node If tag is verified, accept the message Base station can get m = ∑ mi
Else, discard the message End If Algorithm 3 is to be implemented on the base station and base station will finally verify the tag received by the aggregator node and checks the integrity of the messages received with key shared with the leaf nodes.
6. Homomorphic Message Authentication Code (Homo MAC) Based Integrity Support for Secure Data Aggregation
6.1. Homomorphic MAC
Homomorphism in cryptographic operations is very useful in a variety of applications including secure data aggregation. The current research in homomorphism includes homomorphic encryption [18], homomorphic MAC, homomorphic hashing and homomorphic signature. Homomorphic encryption [18] is encryption transformation in that algebraic operations directly applied on encrypted data without applying decryption function on it. The outstanding result of homomorphic encryption is fully homomorphic encryption [19] that allows arbitrary operations on cipher text. In this paper, our focus is on the integrity-preserving alternative that is suitable for secure data aggregation in WSNs.
A homomorphic MAC should satisfy the following properties [20]:
1) Homomorphism. Given two (message, tag) pairs (m1, t1) and (m2, t2), anyone can create a valid tag ta for an aggregated message ma= w1m1 + w2m2 for any scales w1, w2 as weights. Typically, ta= w1t1 + w2t2.
2) Security against Chosen Message Attack. Even under a chosen message attack, in which an adversary is allowed to query tags of polynomial number of messages, it is still infeasible for the adversary to create a valid tag for a message other than a linear combination of some previously queried messages.
A homomorphic MAC consists of three probabilistic, polynomial-time algorithms (Sign, Aggregate, Verify) [20].
1) tu= Sign(k, rid,mu, idu): node u with ID idu, as a contributor of a raw message mu regarding report rid, computes a tag tu for mu using k as the key.
2) Agg = Aggregate((m1, t1, w1), ×××, (mj, tj, wj)): an aggregator implements the homomorphic property for message-tag pairs in the absence of key k, that is, generates a tag t for the aggregated message 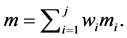
3) Verify(k, rid, m, t): a verifier verifies the integrity of message m regarding report rid by key k and tag t.
In this scheme, all the leaf node and base station share one shared key that is consist of (k1, k2) for end-to-end integrity. We assume the security of the nodes who share key. K1 and K2 denote the key spaces of k1 and k2.  denotes the message space where
denotes the message space where  is the finite field. I denotes the space of node identities and R denote the space of report identifiers. R1 and R2 are two pseudo random functions.
is the finite field. I denotes the space of node identities and R denote the space of report identifiers. R1 and R2 are two pseudo random functions.
Algorithm 1: Leaf Node
// Each leaf node l will computes following Sign(k, rid, ml, idl):
Each leaf node l computes
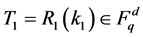

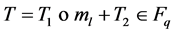
Where о stands for the inner product of two Vectors T1 and ml over finite field 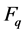 that is, T1 о ml is equal to T1ml,1+ T2ml,2 + ××× + Tdml,d mod q Send this (Tl, ml, wl) to parent node
that is, T1 о ml is equal to T1ml,1+ T2ml,2 + ××× + Tdml,d mod q Send this (Tl, ml, wl) to parent node
wang#title3_4:spAlgorithm 2: Aggregator Node
// Aggregator Node will computes following Aggregate tag generation:
Aggregator Node receives (Tl, ml, wl)
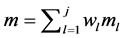
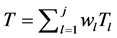
Transmit (m, T) to Base Station
Algorithm 3: Base Station
// Base Station will computes following Verification of tag:
Base station received (m, T) generated by Aggregator Node
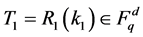
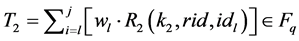
If T1о m+ T2 = T Then integrity verified Else
Discard the message End If In this integrity preserving approach of secure data aggregation, algorithm 1 is to be implemented on the leaf node. In this, each leaf node l computes Tl on the outgoing message ml. And send this (Tl, ml, wl) to aggregator node. Algorithm 2 is to be implemented on the aggregator node. Aggregator node will receive (Tl, ml, wl) from leaf node and generates aggregated tag T and aggregated message m and transmit this (T, m) to the base station. Algorithm 3 is to be implemented on the base station and base station will finally verify the integrity of the messages received with key shared with the leaf nodes.
The security of the homomorphic MAC described in [20] is based on the security of pseudo randomness of R1 and R2. There is probability that, in next run of algorithm, R1 generates same number hence same T1 can be generated and malicious user can have this T1 and generate false T and send that false T to the aggregator node. That may waste the energy of WSNs and decrease the lifetime of WSNs. In [20], authors have proposed the used public key-based pseudo random generator AES [21] to implement R1 and R2. But as we know that public key cryptography is quite expensive and gives much resource overhead, the use of AES is not suitable for secure data aggregation in resource constrained environment of WSNs. Hence, to overcome that, we propose novel solution based on probabilistic bloom filter for pseudo randomness of R1 and R2. Though our approach is simple, it provides intrinsic security to the scheme of homomorphic MAC and thus makes it suitable for secure data aggregation in resource-constrained environment of WSNs. Our scheme of probabilistic bloom filter based homomorphic MAC is discussed in next section.
6.2. Proposed Variant of Homo MAC
As already discussed in Section 6.1, if in the next run of algorithm pseudo random generator R1 generates same number and hence same T1 can be generated and malicious user can have this T1 and generate false T and send this false T to aggregator node. We observed that the space-efficient probabilistic set membership test data structure viz. bloom filter could be employed for the purpose here [22].
Our proposed approach uses a bloom filter [22] based Homo MAC that uses set membership test methods and light-weight hash functions [23] to generate unique k1 and k2 that can be used to generate unique tag T on different messages. Hence, our approach is using different secrets every time to generate different tag T without consuming many resources. The only argument against the usage of the proposed variant could be if at all we have a strong random number generator that ensures non-repetition, is it necessary to employ this variant. However, in that case, Homo MAC remains dependent on the implementation to be secure—the algorithm lacks intrinsic security strength. Hence, our proposal is justified that it enhances the intrinsic security strength of the Homo MAC algorithm without assuming any guarantees from the underlying implementation to make it suitable for resource constrained environment of WSNs.
Following subsection shows the description of bloom filter.
6.2.1. Bloom Filter
A Bloom filter [22], is a space-efficient probabilistic data structure that is used to test whether an element is a member of a set or not. This compressed representation is the payoff for allowing a small rate of false positives in membership queries; that is, queries might incorrectly know an element as member of the set.
Consider a set 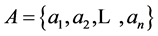 of n elements. Bloom filters describe membership information of A using a bit vector V of length m. For this, k hash functions,
of n elements. Bloom filters describe membership information of A using a bit vector V of length m. For this, k hash functions, 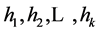 with
with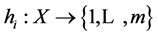 , are used as described below:
, are used as described below:
The following procedure builds an m bits bloom filter, corresponding to a set A and using 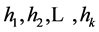 hash functions [22]:
hash functions [22]:
Procedure BloomFilter(set A, hash_functions, integer m)
returns filter filter = allocate m bits initialized to 0 for each ai in A:
for each hash function hj:
filter[hj(ai)] = 1 end for each end for each return filter Therefore, if ai is member of a set A, in the resulting bloom filter all bits obtained corresponding to the hashed values of ai are set to 1. Testing for membership of an element is equivalent to testing that all corresponding bits of bloom filter are set [22]:
Procedure MembershipTest (elm, filter, hash_functions)
returns yes/no for each hash function hj:
if filter[hj(elm)] != 1 return No end for each return Yes As new elements are added to the set, filters can be built incrementally. After that, the corresponding positions are computed through the small hash functions [23] and bits are set in the filter. Moreover, the filter expressing the reunion of two sets is simply computed as the bit-wise OR applied over the two corresponding bloom filters.
6.2.2. A Variant
In this scheme, all the leaf node and base station share one shared key that is consist of (k1, k2) for end-to-end integrity. We assume the security of the nodes that share key. K1 and K2 denote the key spaces of k1 and k2. 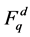 denotes the message space where
denotes the message space where 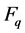 is the finite field. I denotes the space of node identities and R denote the space of report identifiers. R1 and R2 are two pseudo random functions.
is the finite field. I denotes the space of node identities and R denote the space of report identifiers. R1 and R2 are two pseudo random functions.
wang#title3_4:spAlgorithm 1: Leaf Node
// Each leaf node l will computes following Sign(k, rid, ml, idl):
Each leaf node l computes
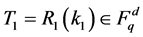
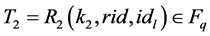
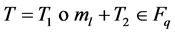
Where о stands for the inner product of two Vectors T1 and ml over finite field 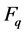 that is, T1о ml is equal to T1ml,1+ T2ml,2 + ××× + Tdml,d mod q Send this (Tl, ml, wl) to parent node
that is, T1о ml is equal to T1ml,1+ T2ml,2 + ××× + Tdml,d mod q Send this (Tl, ml, wl) to parent node
wang#title3_4:spAlgorithm 2: Aggregator Node
// Aggregator Node will computes following Aggregate tag generation:
Aggregator Node receives (Tl, ml, wl)
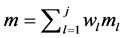
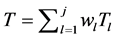
Transmit (m, T) to Base Station
Algorithm 3: Base Station
// Base Station will computes following Create Bloom Filter Call MembershipTest for k1 and k2
If returns yes go to step 1 Else go to next step Verification of tag:
Base station received (m, T) generated by Aggregator Node
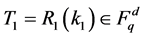
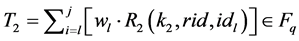
If T1 о m+ T2 = T Then integrity verified Else Discard the message End If Our proposed variant of Homo MAC provides same security as in [20] without assuming security of any external algorithm like AES and hence suitable for integrity preservation for secure data aggregation in WSNs.
7. Implementation Details and Simulation Results
We implement the proposed framework in TinyOS 2.x [24] using nesC [25] as programming language for MicaZ and TelosB motes. For measuring energy consumption of motes in Joules, we used Avrora [26]. We used SHA-1 [27] for MAC generation. In this section, we present simulation results for our implementation.
7.1. Implementation Details
Our implementation is divided in following modules.
MAC: This module contains MAC based hop-by-hop integrity preservation for secure data aggregation using tree topology in WSNs.
AMAC: This module contains aggregate MAC based end-to-end integrity preservation for secure data aggregation using tree topology in WSNs.
Homo MAC: This module contains homomorphic MAC based end-to-end integrity preservation for secure data aggregation using tree topology in WSNs.
A Variant of Homo MAC: This module contains bloom filter based variant of homomorphic MAC for end-to-end integrity preservation for secure data aggregation using tree topology in WSNs.
Figure 2 shows flow graph for our MAC based integrity preservation of secure data aggregation on TinyOS platform and Figure 3 shows flow graph for our proposed variant of Homo MAC based integrity preservation of secure data aggregation in WSNs.
7.2. Results
The memory requirement for our approach is given in Table1 MicaZ mote requires more code memory compared to TelosB because MicaZ has 8-bit AVR micro controller and TelosB has 16-bit MSP-430 micro controller.
Table 2 shows the energy consumption of integrity preserving approaches for secure data aggregation for MicaZ motes in TinyOS.
Figure 4 shows the RAM requirements for various integrity preserving approaches. We show results for MicaZ and TelosB motes. Our variant of Homo MAC requires almost 22% more RAM compared to the original Homo MAC approach of integrity. However, at the same time our approach provides the intrinsic security strength compared to basic Homo MAC.
Figure 5 shows the ROM requirements for various integrity preserving approaches. We show results for MicaZ and TelosB motes. Our variant of Homo MAC requires only 6% more ROM compared to the original Homo MAC approach of integrity. However, at the same time our approach provides the intrinsic security strength compared to basic Homo MAC.
Figure 6 shows the energy consumption for various integrity preserving approaches using MicaZ motes. Our variant of Homo MAC requires almost same energy consumption as of basic Homo MAC approach of integrity. However, at the same time our approach provides the intrinsic security strength to basic Homo MAC.

Figure 2. Flow graph of our MAC based integrity-preserving scheme.

Figure 3. Flow graph of our proposed variant of Homo MAC based integrity-preserving scheme.
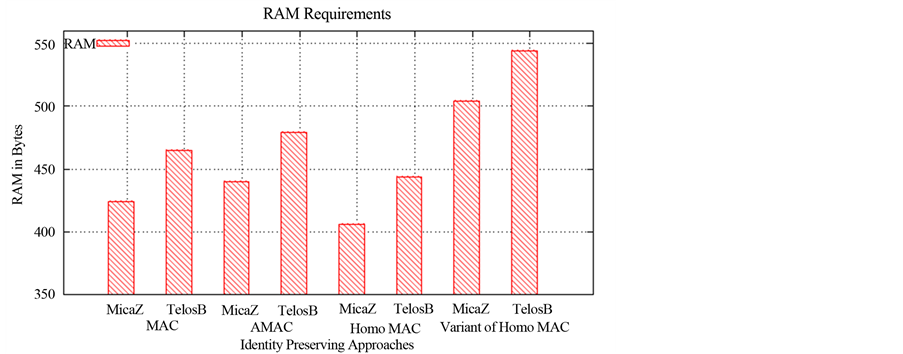
Figure 4. RAM requirements for integrity preserving approaches.
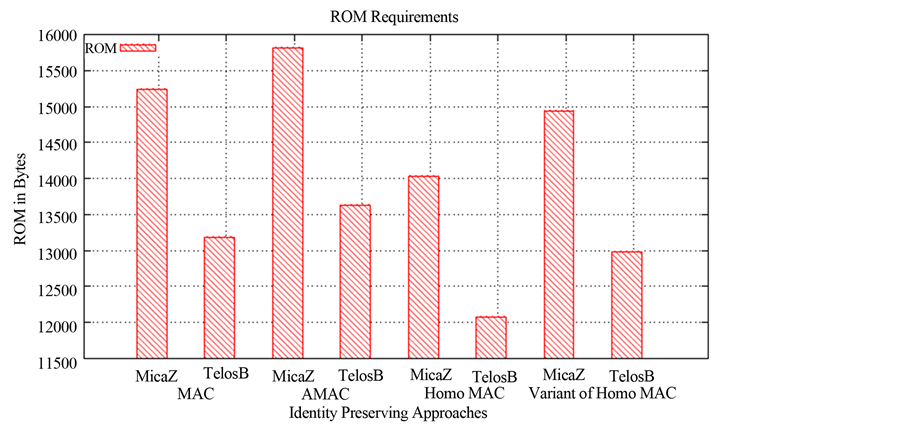
Figure 5. ROM requirements for integrity preserving approaches.
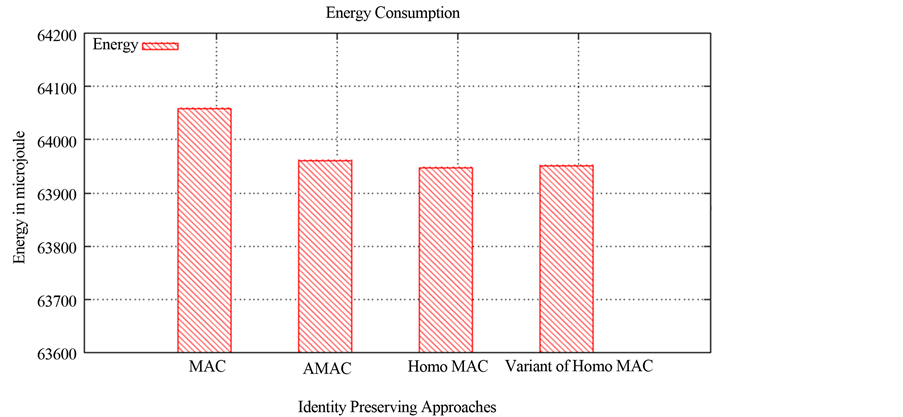
Figure 6. Energy consumption for integrity preserving approaches for MicaZ.
Table 2. Energy consumption for our approaches for MicaZ.
8. Conclusion
In this paper, we investigate three different techniques for integrity preservation in secure data aggregation in wireless sensor networks. We also propose new variant of Homo MAC that improves the intrinsic security strength of basic Homo MAC. Our experimental results show that our variant of Homo MAC requires more energy and storage but that is at the cost of increased intrinsic strength of algorithm.
Acknowledgements
The work contained herein was carried out with support from a sponsored project from the Department of Electronics and Information Technology, Ministry of Communications and Information Technology, Govt of India. The authors remain grateful to the sponsoring agency for the same.
REFERENCES
- F. Akyildiz, W. Su, Y. Sankarasubramaniam and E. Cayirci, “Wireless Sensor Networks: A Survey,” Computer Networks, Vol. 38, No. 4, 2002, pp. 393-422. http://dx.doi.org/10.1016/S1389-1286(01)00302-4
- E. Fasolo, M. Rossi, J. Widmer and M. Zorzi, “In-Network Aggregation Techniques for Wireless Sensor Networks: A Survey,” Wireless Communications, IEEE, Vol. 14, No. 2, 2007, pp. 70-87.
- R. Rajagopalan and P. K. Varshney, “Data Aggregation Techniques in Sensor Networks: A Survey,” Communications Surveys & Tutorials, IEEE, Vol. 8, No. 4, 2006, pp. 48-63. http://dx.doi.org/10.1109/COMST.2006.283821
- C. Karlof and D. Wagner, “Secure Routing in Wireless Sensor Networks: Attacks and Countermeasures,” Proceeding of the First IEEE International Workshop on Sensor Network Protocols and Applications, 2002, pp. 113-127.
- D. Johnson, A. Menezes and S. Vanstone, “The Elliptic Curve Digital Signature Algorithm (ECDSA),” International Journal of Information Security, Vol. 1, No. 1, 2001, pp. 36-63.
- J. Katz and A. Lindell, “Aggregate Message Authentication Codes,” In: T. G. Malkin, Ed., CT-RSA 2008. LNCS, Springer, Heidelberg, 2008, pp. 155-169.
- S. Agrawal and D. Boneh, “Homomorphic MACs: MACBased Integrity for Network Coding,” Proceeding of ACNS 2009, LNCS, Vol. 5536, 2009, pp. 292-305.
- L. Hu and D. Evans, “Secure Aggregation for Wireless Networks,” Proceedings of Applications and the Internet Workshops, 2003, pp. 384-391.
- P. Jadia and A. Mathuria, “Efficient Secure Aggregation in Sensor Networks,” In: V. K. Prasanna, Eds., Proceeding of Boug´e, L., HiPC 2004, LNCS, Springer, Heidelberg, 2004, pp. 40-49.
- Y. Yang, X. Wang, S. Zhu and G. Cao, “SDAP: A Secure Hop-by-Hop Data Aggregation Protocol for Sensor Networks,” Proceedings of the 7th ACM International Symposium on Mobile ad hoc Networking and Computing, 2006, pp. 356-367.
- I. Rodhe and C. Rohner, “n-LDA: n-Layers Data Aggregation in Sensor Networks,” Proceedings of 28th International Conference on Distributed Computing Systems Workshops, ICDCS’08, IEEE, 2008, pp. 400-405.
- B. Przydatek, D. Song and A. Perrig, “SIA: Secure Information Aggregation in Sensor Networks,” Proceedings of the First International Conference on Embedded Networked Sensor Systems, Los Angeles, 2003, pp. 255-265. http://dx.doi.org/10.1145/958491.958521
- M. Bagaa, Y. Challal, A. Ouadjaout, N. Lasla and N. Badache, “Efficient Data Aggregation with Innetwork Integrity Control for WSN,” Journal of Parallel and Distributed Computing, Vol. 72, No. 10, 2012, pp. 1157-1170. http://dx.doi.org/10.1016/j.jpdc.2012.06.006
- V. Jariwala and D. Jinwala, “Evaluating Homomorphic Encryption Algorithms for Privacy in Wireless Sensor Networks,” International Journal of Advancements in Computing Technology, Vol. 3, No. 6, 2011, pp. 215-223. http://dx.doi.org/10.4156/ijact.vol3.issue6.25
- M. Bellare, J. Kilian and P. Rogaway, “The Security of the Cipher Block Chaining Message Authentication Code,” Journal of Computer and System Sciences, Vol. 61, No. 3, 2000, pp. 362-399. http://dx.doi.org/10.1006/jcss.1999.1694
- M. Bellare, R. Canetti and H. Krawczyk, “Keying Hash Functions for Message Authentication,” In: N. Koblitz, Ed., Proceeding of the CRYPTO 1996, LNCS, Springer, Heidelberg, 1996, pp. 1-15.
- D. Jinwala, D. Patel and K. Dasgupta, “Optimizing the Block Cipher and Modes of Operations Overhead at the Link Layer Security Framework in the Wireless Sensor Networks,” Proceedings of the Information Systems Security, Lecture Notes in Computer Science (LNCS), Springer, Berlin Heidelberg, 2008, pp. 258-272.
- C. Fontaine and F. Galand, “A Survey of Homomorphic Encryption for Nonspecialists,” EURASIP Journal on Information Security, Vol. 2007, No. 1, 2007, pp. 1-15.
- C. Gentry, “Fully Homomorphic Encryption Using Ideal Lattices,” Proceedings of the 41st Annual ACM Symposium on Theory of Computing, 2009, pp. 169-178.
- Z. J. Li and G. Gong, “Data Aggregation Integrity Based on Homomorphic Primitives in Sensor Networks,” Proceeding of the Ad-Hoc, Mobile and Wireless Networks, Lecture Notes in Computer Science, Springer, Berlin Heidelberg, 2010, pp. 149-162.
- J. Daemen and V. Rijmen, “The Design of Rijndael: AES —The Advanced Encryption Standard,” Springer, Heidelberg, 2002.
- B. Bloom, “Space/Time Trade-Offs in Hash Coding with Allowable Errors,” Communications of the ACM, Vol. 13 No. 7, 1970, pp. 422-426.
- J. Lawrence Carter and M. N. Wegmanan, “Universal Classes of Hash Functions,” Journal of Computer and System Sciences, Vol. 18, 1979, pp. 143-154.
- J. Hill, et al., “System Architecture Directions for Networked Sensors,” Proceedings of 9th Intl. Conf. on Architectural Support for Programming Languages and Operating Systems (ASPLOS 2000), ACM Press, 2000, pp. 93-104.
- D. Gay, P. Levis, R. von Behren, M. Welsh, E. Brewer, and D. Culler, “The nesC Language: A Holistic Approach to Network Embedded Systems,” Proceedings of Programming Language Design and Implementation (PLDI), 2003.
- B. L. Titzer, D. Lee and J. Palsberg, “Avrora: Scalable Sensor Network Simulation with Precise Timing,” Proceedings of the 4th Intl. Conf. on Information Processing in Sensor Networks (IPSN), 2005, pp. 477-482.
- “Federal Information Processing Standards. Secure Hash Standard. FIPS PUB 180-2,” 2002.


