Journal of Information Security
Vol. 4 No. 3 (2013) , Article ID: 34445 , 9 pages DOI:10.4236/jis.2013.43015
Diffusion Analysis of Message Expansion in STITCH-256
1College of Information Technology, Universiti Tenaga Nasional, Kajang, Malaysia
2Faculty of Computer Science and Information Technology, Universiti Putra Malaysia, Seri Kembangan, Malaysia
3Cryptography Lab, MIMOS Berhad, Technology Park Malaysia, Bukit Jalil, Malaysia
Email: norziana@uniten.edu.my, ramlan, Izura, zuriati@fsktm.upm.edu.my, reza.zaba@mimos.my
Copyright © 2013 Norziana Jamil et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 7, 2013; revised June 9, 2013; accepted June 17, 2013
Keywords: STITCH-256; Message Expansion; Diffusion; Hash Function
ABSTRACT
Cryptographic hash functions are built up from individual components, namely pre-processing, step transformation, and final processing. Some of the hash functions, such as SHA-256 and STITCH-256, employ non-linear message expansion in their pre-processing stage. However, STITCH-256 was claimed to produce high diffusion in its message expansion. In a cryptographic algorithm, high diffusion is desirable as it helps prevent an attacker finding collision-producing differences, which would allow one to find collisions of the whole function without resorting to a brute force search. In this paper, we analyzed the diffusion property of message expansion of STITCH-256 by observing the effect of a single bit difference over the output bits, and compare the result with that of SHA-256. We repeated the same procedure in 3 experiments of different round. The results from the experiments showed that the minimal weight in the message expansion of STITCH-256 is very much lower than that in the message expansion of SHA-256, i.e. message expansion of STITCH-256 produce high diffusion. Significantly, we showed that the probability to construct differential characteristic in the message expansion of STITCH-256 is reduced.
1. Introduction
Recent advances in the cryptanalysis of hash functions [1-12], to name a few, have led to the unexpected failure of some popular algorithms, such as MD4, MD5, SHA-0, SHA-1, HAVAL-128, and RIPEMD. From this cryptanalysis, we understand that these broken hash functions can have two distinct messages yielding the same hash value, known as a collision. The new cryptanalysis techniques introduced by Wang et al. [13-16] provided this breakthrough in cryptography, finding collisions for MD4, MD5, SHA-0, SHA-1, HAVAL-128, and RIPEMD. It was found that the most successful attack on these hash functions is a differential attack, whereby a difference in the messages leads to zero difference in the output of the hash function. In other words, the collision is obtained by constructing a collision path, or characteristic, that fulfills certain conditions with respect to the message differences. In SHA-0, SHA-1, and the MD-family of hash functions, a message with a small difference in the expanded keys is first obtained. This is then used to construct a collision path in the step transformation. This paper focuses only on the first part, which is the message expansion.
Briefly, message expansion in the SHA-family is performed by recursive expansion. In SHA-1, for example, the message expansion accepts a 512-bit input that is divided into sixteen 32-bit words . Sixty-four additional expanded message words are generated as follows:
. Sixty-four additional expanded message words are generated as follows:
Message expansion in SHA-1 differs from that of SHA-0 only in the rotation of one bit to the left. The 80 words can be considered to constitute a linear code over F2. Due to the quasi-cyclic nature of message expansion in SHA-0 and SHA-1, the full collision path can easily be constructed, as in the attack by Wang et al. This can be seen, for example, in SHA-0 message expansion, where differential characteristics with a probability of 1 can easily be constructed in the first 16 steps, as a single bit difference affects fewer than 28 bits in the output. In SHA-1, the code gives a minimum weight of no more than 44 for the full rounds. These traits were exploited by Wang et al. in order to find a collision path for the whole hash function with a complexity of 269 hash operations [14].
As a consequence of the work by Wang et al., the MD-family and SHA-0/1 hash functions are no longer suitable for secure communications. SHA-256 has now become the recommended hash function for many applications that require secure communication. The message expansion in SHA-256 is slightly different from its predecessors. It is the first hash function to use nonlinear modular addition in its message expansion, and successfully increases the minimum Hamming weight of the output bits from 44 (in a full round of SHA-1 message expansion) to 507 for a single-bit difference over a full round. To the best of our knowledge, no optimal lower bound on the minimum weight of the output bits has yet been found by the cryptographic community. However, it is important to have a high minimum weight for a single-bit difference over a full round of message expansion to prevent an attacker from constructing a collision path. This is because of a useful heuristic, often used in the analysis of SHA-0 and SHA-1, suggests that each weight of the output bits lowers the probability of successful collision characteristics by, on average, a factor of 2−2.5 [6].
STITCH-256 [17] is a dedicated cryptographic hash function that also employs message expansion as a source of diffusion. In this paper, we describe the message expansion process in STITCH-256 and compare it with that in SHA-256. This paper is organized as follows: In Sections 2 and 3, we briefly describe the message expansion methods of SHA-256 and STITCH-256, respectively. We then analyze the diffusion property of the two message expansion procedures in Section 4, and show that the minimum weight of the STITCH-256 output bits is higher than the minimum weight of the SHA-256 output bits. Finally, we offer some concluding remarks in Section 5.
2. Message Expansion of SHA-256
In this section, we briefly describe the message expansion process of SHA-256. We use the notation shown in Table 1 throughout this paper.
In SHA-256, the pre-processing involves padding followed by message expansion. A message of arbitrary length is first padded to form multiple 512-bit message blocks. Each of the message blocks is denoted by a row vector m represented by sixteen 32-bit words, . The input message is then expanded to sixty four 32-bit words by the message expansion process, and this can be considered as a 2048-bit expanded message row vector w. The message words Wt are defined as follows:
. The input message is then expanded to sixty four 32-bit words by the message expansion process, and this can be considered as a 2048-bit expanded message row vector w. The message words Wt are defined as follows:
Table 1. Notation.
where  and
and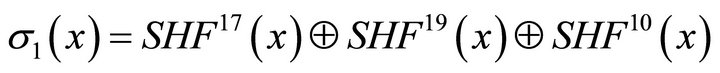 .
.
In total, there are 144 addition (modulo 32) operations and 192 XOR, rotation, and shift operations used in the message expansion of SHA-256.
3. Message Expansion of STITCH-256
In this section, we describe the message expansion procedure of STITCH-256. We use the notation in Table 1. In STITCH-256, the pre-processing again involves padding, whereby the arbitrary length message is extended to an exact multiple of 512-bits. This is followed by the message expansion, which works as follows:


where

and 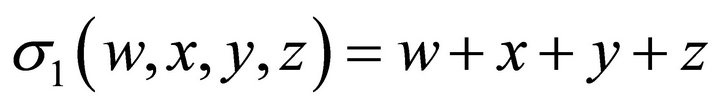
We use two salt values to support the message expansion of STITCH-256, where SV0 = 67452301 and SV1 = 41083726. In the message expansion of STITCH-256, every sixteen message words are taken into account to form the (i-16)-th message word. This is to maximize the bit propagation in the message expansion of STITCH-256. The bit rotations in the message expansion of STITCH-256 are carefully selected to increase the diffusion to the whole message expansion. The message expansion of STITCH-256 is illustrated as in Figure 1.
In STITCH-256, the 512-bit message input is expanded to thirty-two 32-bit message words. This gives the output of message expansion as 1024 bits. All the message words 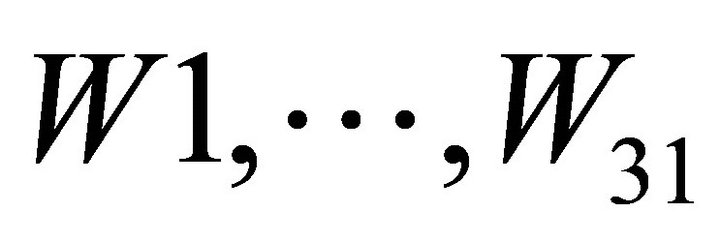 are then reordered to cater to
are then reordered to cater to

Figure 1. Message expansion in STITCH-256.
different message ordering in each line. The compression function of STITCH-256 requires eight  for the whole function as described earlier and the orderings are depicted in Figure 2.
for the whole function as described earlier and the orderings are depicted in Figure 2.
Figure 2 shows the input order of message words  applied to Bj (1 £ j £ 4) branches. The number with an asterisk denotes the message words Wi for 16 £ i £ 31. This means 1’ refers to message words W16, 2’ refers to message word W17, so on and so forth.
applied to Bj (1 £ j £ 4) branches. The number with an asterisk denotes the message words Wi for 16 £ i £ 31. This means 1’ refers to message words W16, 2’ refers to message word W17, so on and so forth.
4. Finding Lowest Weight in the Message Expansion of SHA-256 and STITCH-256
In this analysis, we want to find the low weight in the message expansion of STITCH-256 and compare it with that of SHA-256. We compare with SHA-256 as both formulas used in the message expansion of STITCH-256 and SHA-256 are non-linear recursive functions, in which the formula used in the message expansion of STITCH-256 is inspired from the formula used in the message expansion of SHA-256. To do this, we investigate the effect of a single bit difference at j-th bit of a message word to the whole message words. We consider variants of SHA-256 and STITCH-256 message expan0 sions from a reduction to 32, 64 and 80 steps. We used all-zero vector as the sample data. Then, a single bit is flipped and we record the Hamming weight in the output bit. We repeat this procedure until all the individual input bits are flipped. The results of the experiments are shown in the following sections.
4.1. Experiment 1:32 Rounds of Message Expansion
We show the results of the number of affected bits for a single bit difference in both STITCH-256 and SHA-256 algorithms, running in 32 rounds each. The results are depicted in two types of reading, i.e. at bit level as in Figure 3 and Figure 5, and at byte level as in Figure 4
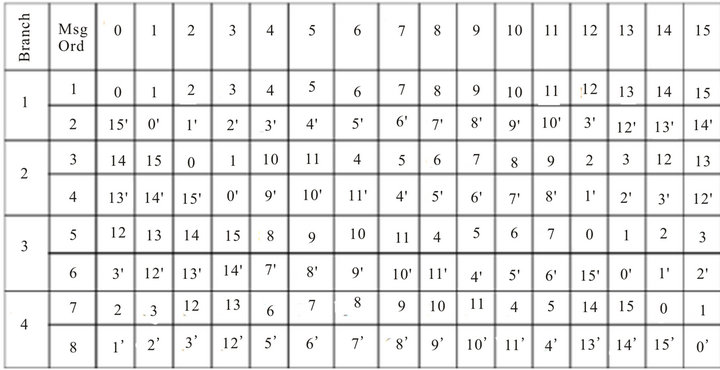
Figure 2. Message orderings for four branches in STITCH-256.
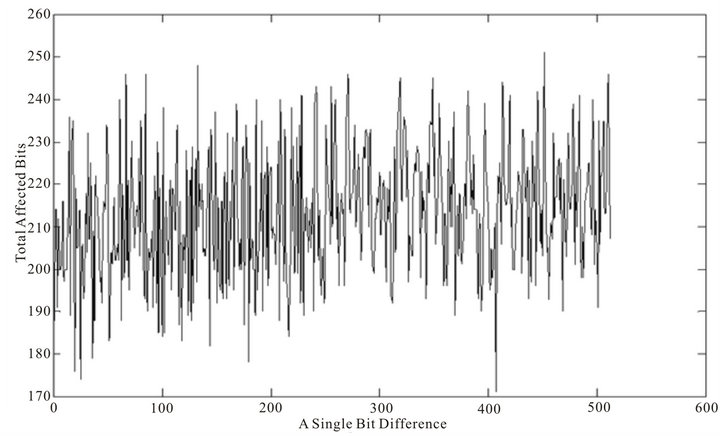
Figure 3. Diffusion property of 32 rounds of STITCH-256 message expansion at bit level.

Figure 4. Diffusion property of 32 rounds of STITCH-256 message expansion at byte level.
and Figure 6.
4.2. Experiment 2:64 Rounds of Message Expansion
We show the results of the number of affected bits for a single bit difference in both STITCH-256 and SHA-256 algorithms, running in 64 rounds each. The results are depicted in two types of reading, i.e. at bit level as in Figure 7 and Figure 9, and at byte level as in Figure 8 and Figure 10.
4.3. Experiment 3:80 Rounds of Message Expansion
We show the results of the number of affected bits for a single bit difference in both STITCH-256 and SHA-256 algorithms, running at 80 rounds each. The results are depicted in two types of reading, i.e. at bit level as in Figure 11 and Figure 13, and at byte level as in Figure 12 and Figure 14.
For a particular round of message expansions for both algorithms, two types of graph reading are shown as above; the first figure (or upper figure, for e.g. in Figure 3) in each of the algorithm shows a single-bit difference versus the total number of affected bits, while the second figure (or lower figure, for e.g. in Figure 4) shows a single bit difference versus the affected bytes. Note, that in the first graph of all the variants of SHA-256, there is a pattern to the total number of affected bits that decreases as the position of single-bit difference increase. This is in
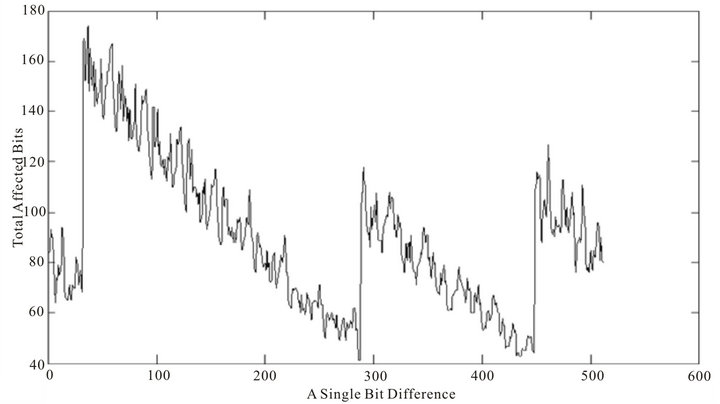
Figure 5. Diffusion property of 32 rounds of SHA-256 message expansion at bit level.

Figure 6. Diffusion property of 32 rounds of SHA-256 message expansion at byte level.
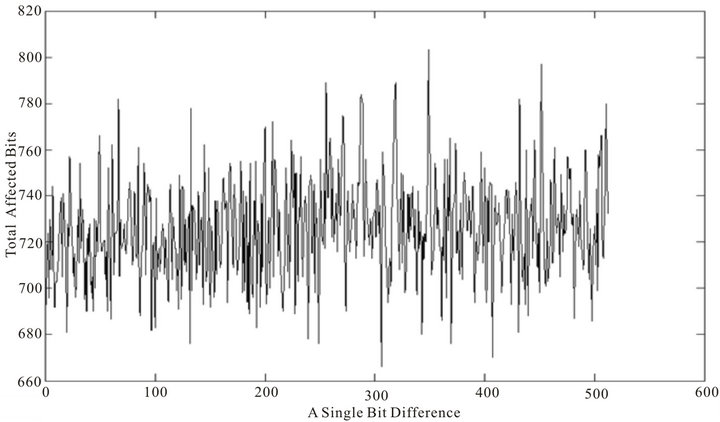
Figure 7. Diffusion property of 64 rounds of STITCH-256 message expansion at bit level.

Figure 8. Diffusion property of 64 rounds of STITCH-256 message expansion at byte level.
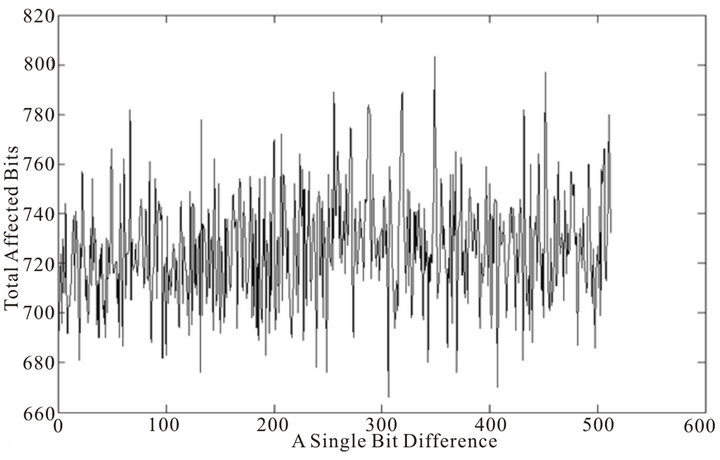
Figure 9. Diffusion property of 64 rounds of SHA-256 message expansion at bit level.

Figure 10. Diffusion property of 64 rounds of SHA-256 message expansion at byte level.
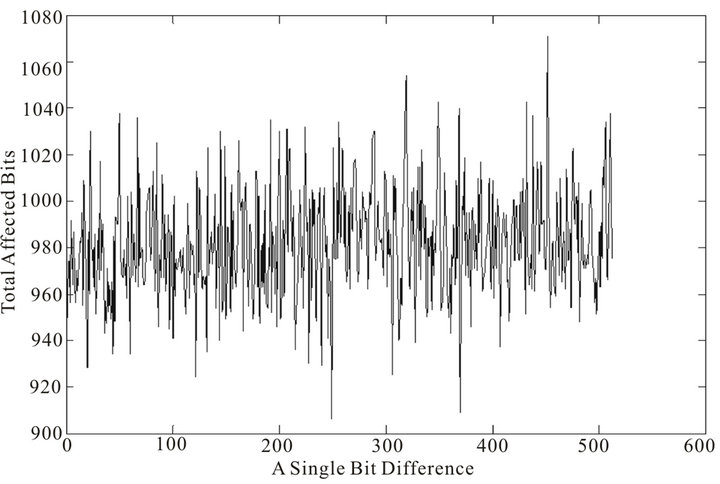
Figure 11. Diffusion property of 80 rounds of STITCH-256 message expansion at bit level.
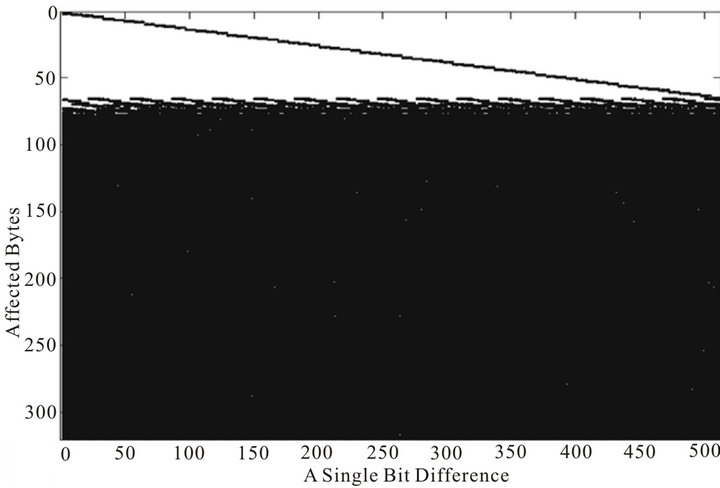
Figure 12. Diffusion property of 80 rounds of STITCH-256 message expansion at byte level.
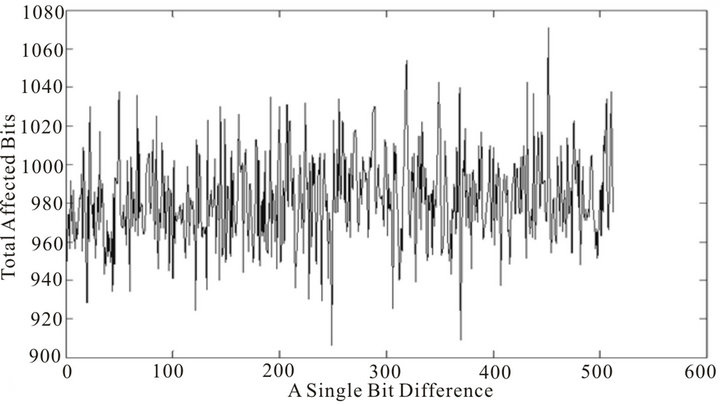
Figure 13. Diffusion property of 80 rounds of SHA-256 message expansion at bit level.
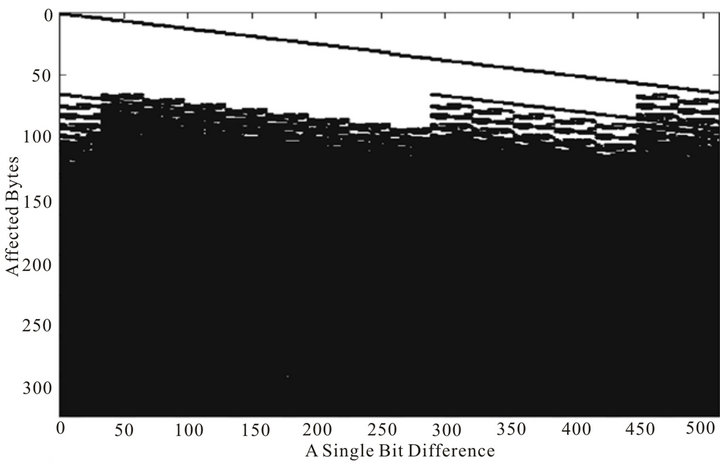
Figure 14. Diffusion property of 80 rounds of SHA-256 message expansion at byte level.
contrast to the message expansion of STITCH-256 which does not show any predictable pattern as the single-bit difference changes. This randomness presents some difficulties to an attacker seeking to fulfill the condition of chaining variables in the first step of the compression, as the distribution of bit propagation seems to be unpredictable and more bits are affected by a single-bit difference.
Table 2 shows the average number of affected bits for a single bit difference in the message expansion of both STITCH-256 and SHA-256. As shown in Table 2, the average number of affected bits for a single bit difference in the message expansion of STITCH-256 is higher than that of SHA-256. It can be seen that the message expansion of STITCH-256 produces, on average, more than 100 bits in the output get affected for a single bit flipping in input. We then find the lowest minimum weight in the output of message expansion for both algorithms when a single bit in input is flipped. Table 3 shows the result of lowest minimum weight from the message expansion formula in STITCH-256 and SHA-256 algorithms. The lowest minimum weight for both algorithms is increasing and different for different rounds.
From the result shown in Table 3, it can be seen that the formula used in the message expansion of STITCH-256 produces larger lowest minimum weight in the
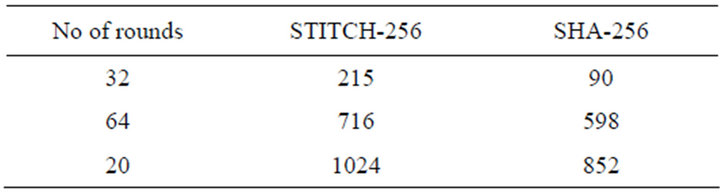
Table 2. An average number of affected bits for a single bit difference in the message expansion of STITCH-256 and SHA-256.
output than that of SHA-256 for different rounds. In principle, a larger minimum weight implies that the differential cryptanalysis of the compression function will be more complex [18]. Finally, we derive lower and upper bounds for the probability of a successful differential collision characteristic in STITCH-256. These are shown in Table 4. To the best of our knowledge, no optimal lower bound on the minimum weight of the output bits has yet been found by the cryptographic community. However, it is important to have a large minimum weight for a single-bit difference over a full round of message expansion to prevent an attacker from constructing a collision path. This is because useful heuristic, often used in the analysis of SHA-0 and SHA-1, suggests that each weight of the output bits lowers the probability of successful collision characteristics by, on average, a factor of 2−2.5 [16].
5. Conclusion
In this paper, we analyzed the effect of a single-bit difference (or the diffusion property) of the message expansion process of STITCH-256, and compared it with that of SHA-256. It is shown that the number of affected bits in output is higher in the message expansion of STITCH-256 than that of SHA-256, thus telling us that the diffusion of the message expansion of STITCH-256 is
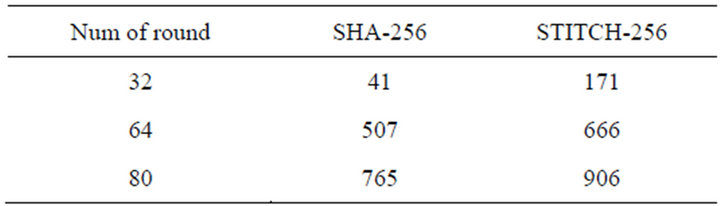
Table 3. Minimum weight of message expansion in STITCH-256 and SHA-256.
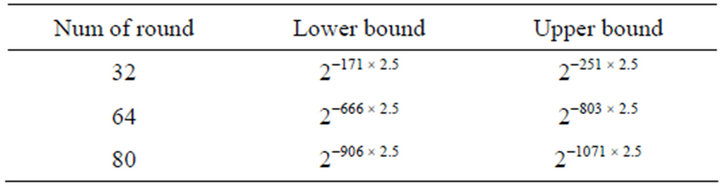
Table 4. Lower and upper bound for probability of successful differential collision attack in STITCH-256.
better than the message expansion of SHA-256. Both message expansions of STITCH-256 and SHA-256 employ addition modulo 232, which means no linear code can be constructed for them. The high diffusion in the message expansion of STITCH-256 as shown in the lower bound derived for the probability of successful differential collision characteristics tells that it is infeasible to construct such a collision characteristics even in the message expansion of STITCH-256.
REFERENCES
- K. Aoki, J. Guo, K. Matusiewicz, Y. Sasaki and L. Wang, “Preimages for Step-Reduced SHA-2,” In: M. Mitsuri, Ed., Advances in Cryptology—ASIACRYPT 2009, Springer, Berlin, 2009, pp. 578-597. doi:10.1007/978-3-642-10366-7_34
- E. Biham and R. Chen, “Near-Collisions of SHA-0,” In: M. Franklin, Ed., Advances in Cryptology—Crypto 2004, Springer, Berlin, 2004, pp. 290-305. doi:10.1007/978-3-540-28628-8_18
- E. Biham and R. Chen, “New Results on SHA-0 and SHA- 1,” 2004.
- A. Biryukov, M. Lamberger, F. Mendel and I. Nikolic, “Second-Order Differential Collisions for Reduced SHA- 256,” In: D. H. Lee and X. Y. Wang, Eds., Advances in Cryptology—ASIACRYPT 2011, Springer, Berlin, 2011, pp. 270-287. doi:10.1007/978-3-642-25385-0_15
- F. Chabaud and A. Joux, “Differential Collisions in SHA- 0,” In: H. Krawczyk, Advances in Cryptology—Crypto’ 98, Springer, Berlin, 1998, pp. 56-71. doi:10.1007/BFb0055720
- E. Grechnikov, “Collisions for 72-Step and 73-Step SHA- 1: Improvements in the Method of Characteristics,” 2010. http://eprint. iacr.org.
- V. Rijmen and E. Oswald, “Update on SHA-1,” In: A. J. Menezes, Ed., Topics in Cryptology—CTRSA 2005, Springer, Berlin, 2005, pp. 58-71. doi:10.1007/978-3-540-30574-3_6
- K. Matusiewicz and J. Pieprzyk, “Finding Good Differential Patterns for Attacks on SHA-1,” In: Ø. Ytrehus, Ed., Coding and Cryptography, Springer, Berlin, 2006, pp. 164-177. doi:10.1007/11779360_14
- S. Manuel and T. Peyrin, “Collisions on SHA-0 in one Hour,” In: K. Nyberg, Ed., Fast Software Encryption, Springer, Berlin, 2008, pp. 16-35. doi:10.1007/978-3-540-71039-4_2
- Y. Sasaki, L. Wang and K. Aoki, “Preimage Attacks on 41-Step SHA-256 and 46-Step SHA-512,” 2009. http://eprint.iacr.org/2009/479.pdf
- M. Stevens, “Single-Block Collision Attack on MD5,” 2012. http://eprint.iacr.org/2012/040.pdf
- T. Xie and D. Feng, “Construct MD5 Collisions Using Just a Single Block of Message,” 2010. http://eprint.iacr.org/2010/643.pdf
- X. Wang, D. Feng, X. Lai and H. Yu, “Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD,’ 2004.
- X. Wang, Y. Yin and H. Yu, “Finding Collisions in the Full SHA-1,” In: V. Shoup, Ed., Advances in Cryptology—Crypto 2005, Springer, Berlin, 2005, pp. 17-36. doi:10.1007/11535218_2
- X. Wang, H. Yu and Y. Yin, “Efficient Collision Search Attacks on SHA-0,” In: V. Shoup, Ed., Advances in Cryptology—Crypto 2005, Springer, Berlin, 2005, pp. 1- 16. doi:10.1007/11535218_1
- C. Jutla and A. Patthak, “A Simple and Provably Good Code for SHA Message Expansion,” 2005.
- N. Jamil, R. Mahmod, M. Zaba, N. Udzir and Z. Zukarnain, “STITCH-256: A Dedicated Cryptographic Hash Function,” Journal of Applied Sciences, Vol. 12, 2012, pp. 1526-1536. doi:10.3923/jas.2012.1526.1536
- J. Liu, H. Jiang and S. Huang, “Nonlinear Message Expansion for Hash Function,” Computer Science and Information Technology, 2008, pp. 779-784.

