Journal of Information Security
Vol. 3 No. 2 (2012) , Article ID: 18767 , 8 pages DOI:10.4236/jis.2012.32008
Hardware Performance Evaluation of SHA-3 Candidate Algorithms
1Computer Science Department, Jordan University of Science and Technology (CHiS), Irbid, Jordan
2Cryptographic Hardware and Information Security Lab (CHiS), Computer Engineering Department, Jordan University of Science and Technology, Irbid, Jordan
3Engineering Mathematics & Internetworking, Dalhousie University, Halifax, Canada
Email: {yijararweh, tawalbeh}@just.edu.jo, hala.t.88@hotmail.com, Abidalrahman.Mohd@dal.ca
Received October 25, 2011; revised December 5, 2011; accepted January 9, 2012
Keywords: Information Security; Secure Hash Algorithm (SHA); Hardware Performance; FPGA
ABSTRACT
Secure Hashing Algorithms (SHA) showed a significant importance in today’s information security applications. The National Institute of Standards and Technology (NIST), held a competition of three rounds to replace SHA1 and SHA2 with the new SHA-3, to ensure long term robustness of hash functions. In this paper, we present a comprehensive hardware evaluation for the final round SHA-3 candidates. The main goal of providing the hardware evaluation is to: find the best algorithm among them that will satisfy the new hashing algorithm standards defined by the NIST. This is based on a comparison made between each of the finalists in terms of security level, throughput, clock frequancey, area, power consumption, and the cost. We expect that the achived results of the comparisons will contribute in choosing the next hashing algorithm (SHA-3) that will support the security requirements of applications in todays ubiquitous and pervasive information infrastructure.
1. Introduction
Cryptographic hash functions are very important for many security applications, especially for the authentication related applications, such as message authentication codes, password protection and digital signature. Data integrity verification is another field in which cryptographic hashing takes place. It is used to make sure that the data transmitted within a message is not being accessed or modified.
Secure hashing algorithms take a block of data (message), and return a fixed size bit string (hash value), such that any change on data leads to a change on the hash value (digest). This can be considered as a scenario that describes briefly the mechanism of the secure hashing algorithm. Figure 1 shows this scenario. First, conversion of data and associated password into a digests, then it will be compared in order to make sure that the message is safe and well protected.
SHA robustness depends mainly on many factors. Among them is the ease of computing the hash value, the infeasibility of generating a message that has given a hash, the infeasibility of modifying a message without altering its hash. Adding to that, is the infeasibility of finding two different messages with the same hash value. Secure hashing algorithms not only protect data from theft or alteration, but also it can be used to ensure user authentication. SHA are used to provide digital fingerprint of file contents, and can be employed by many operating systems to encrypt and decrypt passwords. Current secure hashing algorithms e.g. SHA1 and SHA2 are very essential, and widely used for secure communications, even in wireless communications [1]. However, it shows many weakness and limitations that trigger the need to find an applicable replacement.
NIST held a competition of three rounds in order to find a new secure hash algorithm. The new algorithm must overcome the limitations of the previous secure hash algorithms. Now, we are in the final round with five candidates. The main goal of this paper is to find the best algorithm among the five candidates (Blake, Grostl, JH, Keccak and Skein) that reach the final round of the competition. The final selected algorithm will provide a higher level of security considering the cost and the complexity aspects. The selection of the best algorithm will be based on a hardware evaluation of the five candidates. The aspects of comparisons are: throughput in Mbps, frequency in MHz, and used area measured in Configurable Logic Blocks (CLBs).
2. Related Work
In recent years, many attacks have been reported against different cryptographic hash functions. In 2005, Xiaoyun
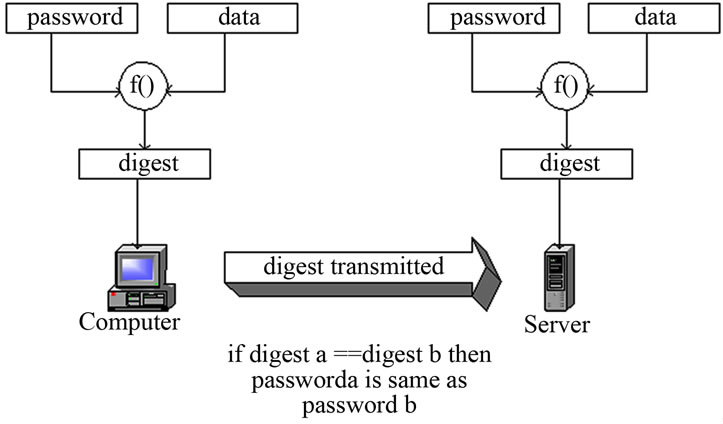
Figure 1. Digest authentication mechanism in hashing algorithms [2].
Wang announced a practical attack for SHA-1 [3]. As a quick response, NIST held a workshop for the purpose of studying the general status of cryptographic hash algorithms. Wang’s attack affects some digital signature applications, time stamping and certificate signing operations [4]. A rapid transition to a new family of hash functions became very essential. SHA-2 was the new hash algorithm with a stronger family of hash functions that were suitable for many commercial applications.
At the same time, SHA-2 had a constraint that is the interoperability with many other systems [5]. In order to find a new cryptographic hash algorithm with a higher level of security and compatibility, NIST decided to hold a public competition to select a replacement algorithm. The main goal of finding new algorithm, is to stop using SHA-1 in digital signature, digital time stamping, and many other applications.
For SHA-2 many work in literature focused on how to optimize speed and throughput [6,7]. Many other works focused on finding a new implantations for SHA-2, or proposing techniques that improves SHA-2 implementations by many techniques, such as: operation rescheduling and area decreasing [7,8].
Another implementation in [9] which consumed 1373 slices for SHA-256 core, and 2726 slices for SHA-512 core with no power results provided. The implementation of [10] used ASIC core for 8-bit SHA-256 core. This is not practical because of the large number of clock cycles which led to a bad performance and more complex control logic. For the under development SHA-3 and its final round candidates (Blake, Grostl, JH, Keccak and Skein), there are many works that studied each one of them.
The work in [11] focused on the implementation of Skein as one of the finalists in order to investigate the performance characteristics resulted of using a different modern of FPGAs architectures.
A major criteria to compare the candidates is the chip area. The research in [12] shows that Skein consumed much less area than other candidates. Another important comparison criteria is the hardware overall performance in modern FPGAs families (Virtex5 and Virtex6 from Xilinx) [13,14]. Other researches evaluate the finalists according to their hardware implementation quality such as in [15].
In [16], candidate’s hardware implementations, evaluations, definitions, and properties were discussed. In general, we can say that the research in [16] is a demonstration for the hardware evaluation process of SHA-3 final round candidates. Other works focused on comparing the algorithms that passed to second round of the competition (CubeHash, ECHO, Fugue, Hamsi, Luffa, Shabal, SHAvite-3, SIMD, Blake, Grostl, JH, Keccak and Skein). In [17], the authors describe, analyze, and rank a SHA3 hardware benchmark process for both FPGAs and ASICs. They come up with some insights about how designer can have different conclusions when working on the same most efficient SHA-3 candidates. Also, they investigated theSHA-3 hardware benchmarking results in different platforms.
Some other researches selected different algorithms of round two candidates, just like [18] that worked on Keccak, Luffa and BMW. They provided an efficient, fast, and high throuput hardware implementations for them. [19] shows the hardware implementations for another set of round two candidates reporting both ASIC and FPGA implantations. This paper provided a ranking for the 5 candidates based on their performance. ASIC evaluations presented in [20,21].
3. SHA 3 Candidate Algorithms
SHA is a group of hash functions approved and published by NIST. All of the current secure hash algorithms are published by the National Security Agency (NSA) [22]. SHA-0 is a 160 bit secure hash function published in 1993. Due to an undisclosed significant flaw, SHA-0 was withdrawn shortly after its publication and replaced directly by SHA-1. SHA-1 is also a 160-bit secure hash function. It is designed, developed, and published by NSA as a part of the digital signature algorithm. SHA1 is the most used algorithm among the hashing algorithms.
SHA2 is a family of two similar hash functions with different 4 block-sizes for the output, 224, 256, 384, and 512-bit. The SHA-224 and the SHA-256 are truncated versions of the SHA-384 and SHA-512. The same as SHA-1, all SHA-2 families were designed, developed, and published by NSA.
On the other hand, SHA-3 is the upcoming hash function which is still under development. It will be published in a public competition held by NIST to choose the best algorithm among all the candidates in March 2012.
3.1. The Need for New SHA
Due to many attacks reported on SHA1. One of these attacks is the deferential attack applied to find a hash collision. It was 130,000 times faster than what was acceptable [23]. NIST decided to develop a new hashing stander that act as a new transition to more reliable and trustworthy hashing algorithm. To achieve this transition, NIST held a public competition started at the first quarter of 2007 [21].
Two years after the announcement, 64 competitors or candidates submitted their hashing algorithms to NIST for Evaluation (51) of them were qualified to compete within the first round. The NIST criteria’s used to evaluate the first round candidates were: security, cost, performance, and algorithms software implementations. The performance of hardware implementations was not considered at this stage.
In the second quarter of 2009, a conference for announcing the 14 candidates who passed to the second round was hosted by NIST. Then, in the second quarter of 2010, the second conference for announcing the winners that passed to the third round was held by NIST. The third round is the final round for this competition with 5 candidates. The criteria’s used to evaluate the candidates in all the rounds were the same. But, for round 3 it was extended to consider the hardware domain since the remaining 5 candidates were implemented in hardware. The winner of this competition will be announced in January 2012 and will be titled as SHA3 [21].
3.2. Common Hashing Algorithms Components
Two primitives are needed to build strong encryption algorithms: confusion and diffusion. Depending on Claude Shannon information theory confusion is the operation by which the relationship between the message and its digest will be kept obscure. On the other hand, diffusion is the operation of spreading the influence of each message bit in order to hide it is statistical property [10].
As it is so obvious, the confusion operation helps in maintain the one way property. While the diffusion helps in strengthen the collision resistance. All the candidates use almost the same components in order to carry out the two primitives of confusion and diffusion. Most of SHAs have common components that can be summarized as follow:
1) Permutation
It is the process of swapping data for the purpose of handling the diffusion operation. Depending on the algorithm itself, the size of data to be swapped will be determined. The data can be swapped in bits within swapping at smaller scales, and can swap multiple words at larger scales.
2) Substitution
It is the process of nonlinear transformation of the input for the purpose of handling the confusion operation, >Usually it is implemented using a substitution-boxes (S-box), which are carefully chosen to be resistant to cryptanalysis.
3) Logical function
Logical functions are performed using logical gates such as AND, OR and NOT. The most desired and commonly used logical function in cryptography is the XOR. And since it has the function of balancing it is impossible to know the input to an XOR with having a look only to its output.
4) Modular arithmetic function
Modular arithmetic functions are used for the purpose of handling the diffusion operation through generation and propagation of the carry. The most desired and commonly used arithmetic operations are the addition and multiplication. Performing this operation is slow due to the carry dependency.
3.3. SHA3 Candidate Algorithms Description
In this subsection, we present the description of each one of the five SHA-3 candidates.
1) Blake
This algorithm met all NIST criteria for SHA3 such as: message digest of 224, 256, 384 and 512 bits, same parameter size of SHA-2, one pass streaming mode, and maximum message length of at least 264-1 bits. Blake deserved to be one of the five finalists [24]. Blake’s designers tried to keep it simple and familiar as possible to all cryptanalysis, since it is combined of well-known and trusted blocks.
Any superfluous features were avoided, and just provide what users really need. Blake can be considered as a family of 4 hash functions, Blake-224, Blake-256, Blake- 384 and Blake-512. Also, Blake has a 32-bit version and a 64-bit version from which other instances are derived. Blake follows the Hash Iterative Framework construction for its iteration mode. Blake implementation requires low resources and its fast in both software and hardware environments [3]. Figure 2 shows a detailed block diagram for BLAKE algorithm [15].
The internal structure of Blake is the local wide-pipe that makes the local collisions impossible for its hash functions. Regarding Blake’s internal state, it is initialized by a set of initial values, counter values, and some constants. The state is updated using G function that contains modular addition, XOR, and rotates operation state [4]. The Blake’s compression algorithm, it is a modified version of stream cipher ChaCha where the round function is based on it.
The message block goes through a permutation process and then enters into the round function. The round function has one layer of G functions with a stored internal state [11 silicon imp of sha3 finalists]. Two layers of G functions each of 4 functions will be used for one round which means that 8 G functions will be implemented.
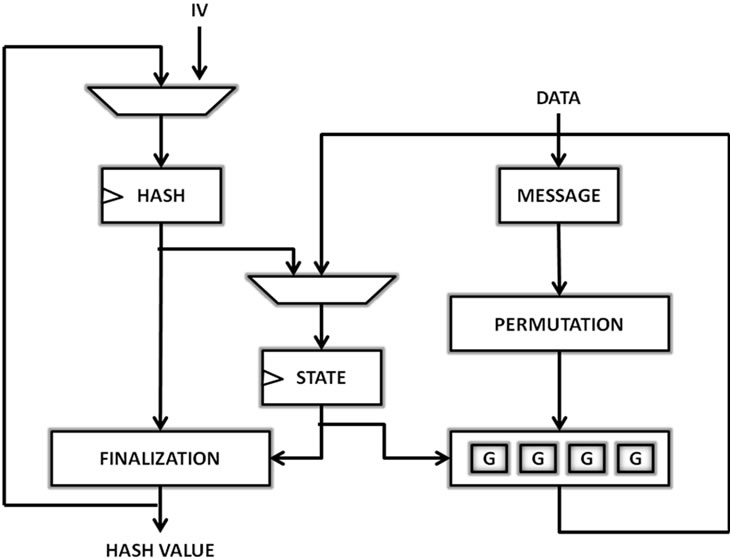
Figure 2. BLAKE algorithm block digram.
Only 4 G functions will be used during the first half of a round. The next 4 G functions along with the output of the first half which is stored in the internal state registers will be used in the other half processing. After each round for a current message block, the finalization process starts, and the chaining value for the next message block will be stored in the internal state registers. The used unrolling of G functions in two layers is important for reducing the latency, and raising the performance at the expense of maximum frequency and area state [13].
2) Groestl
It is an iterated hash function with a compression function. It’s design is based on principles that are very different from those of SHA family [5]. Groestl is a byte-oriented SP-network that borrows components from the AES. The S-box used for Groestl and for AES is identical, and the diffusion layers of Groestl and AES are constructed in same manner. Since Groestl is based on a small number of permutations instead a block cipher with many permutations, it has some design specification as a result of this reduced number of permutations, such as the simplicity of analysis, the secure construction, the side channel resistance, allowing implementers to exploit parallelism within the compression function, and prevention of length extension attacks [22]. Figure 3 shows a detailed block diagram for Groestl [15].
Groestl implements wide-pipe Merkel-Damgard construction which is similar to the plain Merkel-Damgard construction with the size of the internal state registers being different. Groestl has two functions: P and Q which are implemented in parallel. This parallelism leads to hardware resources sharing which results in low area of implementation. Both P and Q include four round functions performing XOR, permutation and substitution. The output of these functions will be the input for the XOR gate and its output will be stored as hash digest [21].
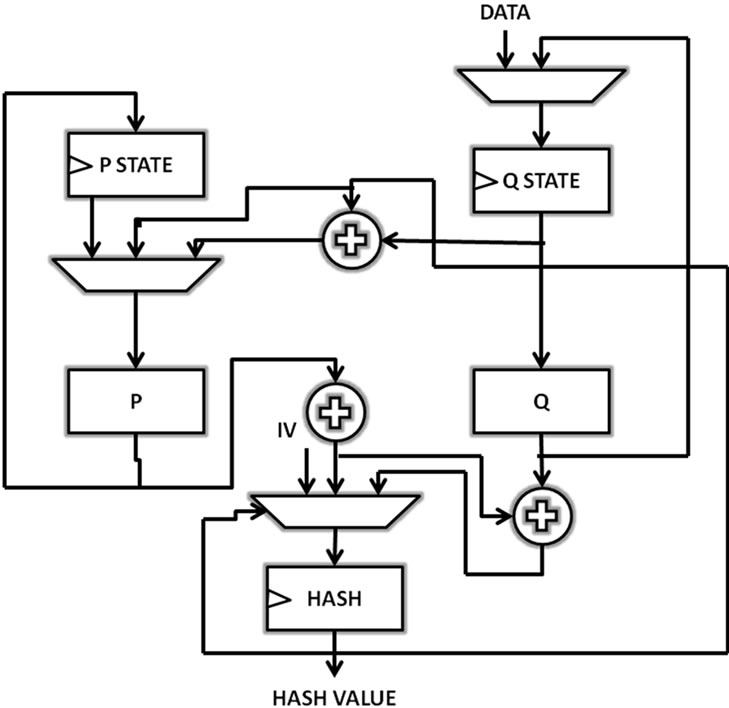
Figure 3. Groestl algorithm block digram.
3) JH
JH is a family of four hash functions, JH-224, JH-256, JH-384 and JH-512. The JH algorithm is efficient for hardware implementation since it is built using simple components, and in software with SIMD instructions and bit slice implementation. The JH compromised function is constructed from a large block cipher with constant key. The operation used are permutation, substitution, and logical XOR. Each input message is XORed twice, the first time before each round function with first half of chaining values. The second time at the end of each round function with second half of the chaining values [24].
JH has two similar modules for round operations: R6 and R8 that are used for the round constant generation and compression, respectively. For R6, the round constant generation can be achieved based on one of two ways, either the round constant from a previous cycle, or the initial constant value. On the other side, in R8, the chaining values are generated depending on the input message, the previous cycles, and the generated round constant. Three different layers are represented in R8, the layer of substitution, the layer of permutation, and the layer of linear transformation [24]. Figure 4 shows a detailed block diagram for JH algorithm [15].
4) Keccak
It is based on the sponge construction [25], so Keccak can be considered as a family of sponge functions. The aims of using the sponge construction are to have a provable security against generic attacks and to make the use of compression function more simple, flexible, and functional. In sponge construction model, there are two portions for the internal stage registers. Also, there are two phases, absorbed and squeezed. The input message will

Figure 4. JH algorithm block digram.
be XORed with the data stored in the first portion of the internal stage registers during the absorption stage. And then the resulted value of the XORing process will be updated along with the data stored in the second portion of the internal stage register. During the squeezing phase, the data of the first portion will be used as a part of the output. It is worth mentioning that the sponge construction can accommodate the output of any size by updating the internal stage register. Figure 5 shows a detailed block diagram for Keccak algorithm [15].
5) Skein
Skeins family has three different internal sizes for its functions 256, 512 and 1024 bits. The main idea of skein is to build a hash function that is out of tweak able block cipher. The skeins design is divided up into three components which are: Threefish, Unique Block Iteration (UBI), and Optional Argument System [4,26]. The Threefish block cipher is composed of subkey, mixing, and permutation, and is used to build the compression function using a modified Mateas-Meyer-Oseas configuration. Figure 6 shows Skein 512-256 [15].
4. Results and Evaluation
The hardware design for SHA-3 candidate algorithms were coded in VHDL in [11]. Xilinx ISE 13.1 was used to synthesize the hardware designs using Virtex-5, Virtex-6 and Virtex-7 FPGA families. Virtex-7 is a new FPGA family based on 28 nm architecture designed for high performance, high throughput, and low power consumption. Virtex-7 power efficiency helps in mitigating the power requirements of the increased design area of the new SHA-3 algorithms compared to SHA-2 area.

Figure 5. Keccak algorithm block digram.

Figure 6. Skein algorithm block digram.
The synthesis results are shown in Tables 1-3. All the results are based on SHA-3 256-bit variants.
Table 1 shows the algorithms operating frequency results for different FPGA families. The results show that using Virtex-7 provides a higher operating frequency comparing with Virtex-5 and 6. JH and KECCAK algorithms show a higher frequency than other SHA-3 and SHA-2 algorithms. In contrast, BLAKE and SKEIN results show lower frequency when compared to SHA-2.
Table 2 shows the algorithms Area results (number of CLBs) for different FPGA families. The results show the use of Virtex-7 results in larger area comparing with Virtex-5 and 6. JH and SKEIN algorithms show a better area results than other SHA-3 candidates. On the other hand, BLAKE and GROESTL results show larger area requirements when compared to other SHA-3 algorithms.
Table 3 shows the algorithms throughput (Mbps) results for different FPGA families. The results show that the using of Virtex-7 has a little impact in on the throughput
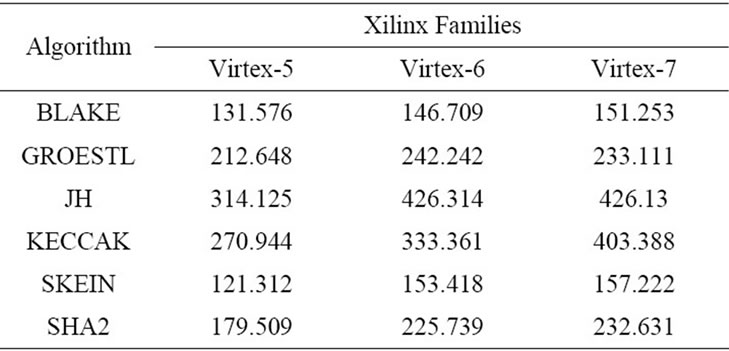
Table 1. Clock frequencies of SHA-3 candidates and SHA 2 algorithm.
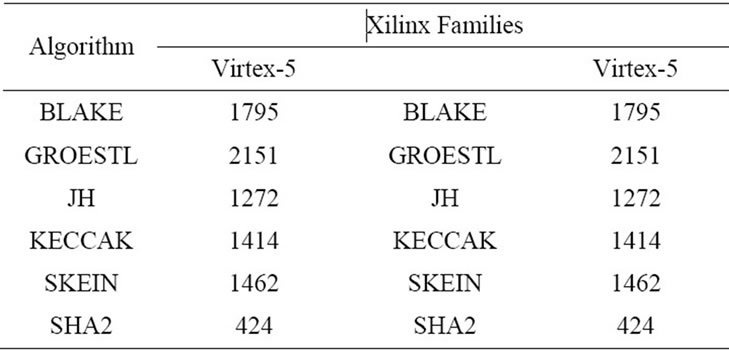
Table 2. Area Results (CLBs) of SHA-3 candidates and SHA-2 algorithm.

Table 3. Throughput results (Mbps) of SHA-3 candidates and SHA-2 algorithm.
comparing with Virtex-5 and 6 except for KECCAK algorithm. JH and KECCAK algorithms show a higher throughput than other SHA-3 and SHA-2 algorithms. KECCAK algorithm shows the best results in term of throughput.
For the purpose of comparison, Figures 7 and 8 show normalized SHA-3 algorithms results with respect to SHA-2 algorithm in terms of throughput and area. Figure 7 shows that all SHA-3 candidates have better throughput compared to SHA-2. KECCAK algorithm outperforms all other SHA-3 algorithms in terms of throughput. Figure 8 shows that all SHA-3 candidates’ required larger area compared to SHA-2. BLAKE and GROESTL algorithms show the worst area results compared to other SHA-3 algorithms. Figure 9 shows the “throughput to area ratio” of SHA-3 candidates normalized to the “throughput to area ratio” of SHA-2. Again, we can see
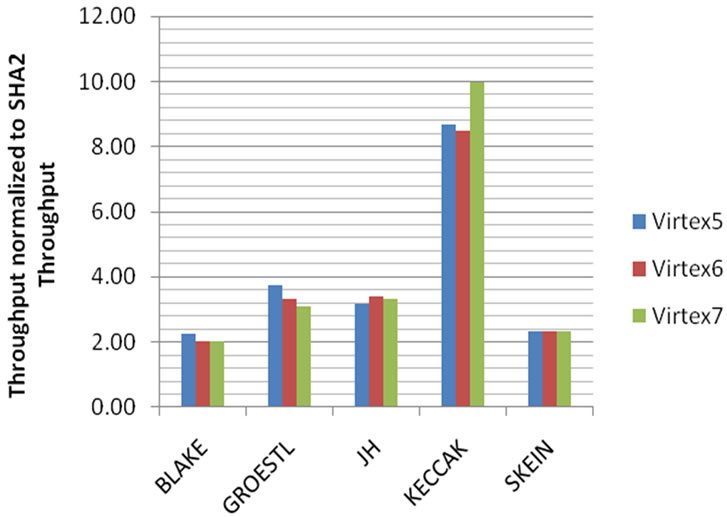
Figure 7. Throughput of SHA-3 candidates normalized to the throughput of SHA 2.
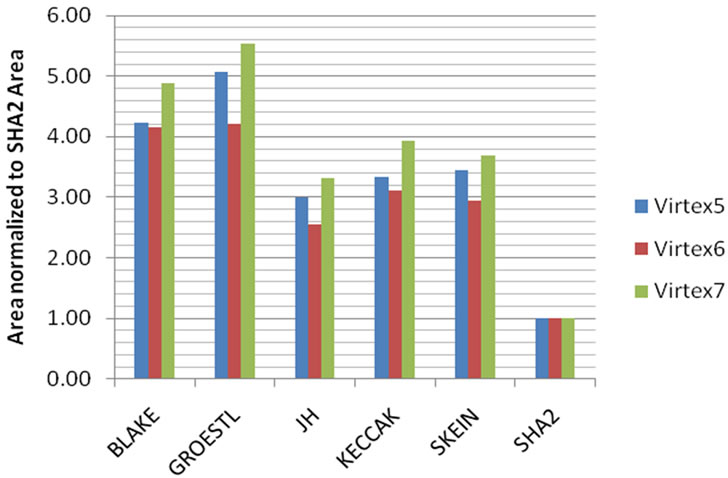
Figure 8. Area of SHA-3 candidates normalized to the area of SHA 2.
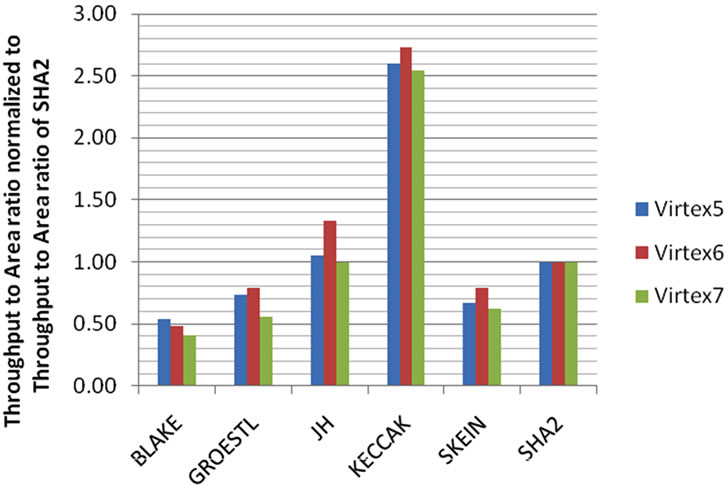
Figure 9. Throughput to Area ratio of SHA-3 candidates normalized to the throughput to area of SHA 2.
that KECCAK algorithm outperform all other SHA-3 algorithms. Figure 10 shows normalized power consumption estimation for the finalist algorithms with respect to SHA-2 for Virtex-6 and Virtex-7. Virtex-7 shows remarkable power efficiency up to 50% of power saving compared to Virtex-6.
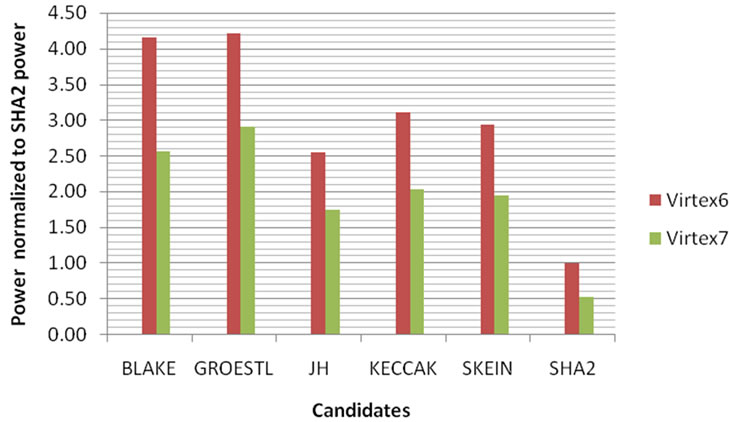
Figure 10. Power consumption of SHA-3 candidates normalized to the power consumption of SHA 2.
Based on the hardware synthesis results, the KECCAK algorithm outperforms all other SHA-3 algorithms. On the other hand, Virtex-7 shows promising results compared with older FPGA families from Xilinx like Virtex-5 and Virtex-6 especially in the power consumption side.
5. Conclusions
The demand on securing information and communication is increasing continuously. Secure Hashing Algorithms (SHA) are considered among the common and powerful cryptographic functions used today.
In this paper, we perform a detailed hardware performance evaluation of the final round SHA-3 candidates (JH, BLAKE, GROESTL, KECCAK and SKEIN). The hardware designs of the 5 algorithms were synthesized using Virtex-5, 6 an 7 FPGA chips to get area, frequency and Throughput results. The KECCAK algorithm outperforms all other SHA-3 algorithms in terms of clock frequency, area, and throughput. On the other side, BLAKE and GROESTL algorithms show the worst performance in terms in throughput, power and area. From obtained results, we conclude that KECCAK algorithm represent the best SHA-3 candidate from the hardware evaluation perspective.
6. Acknowledgements
The authors would like to thank their universities, and the Scientific Research Support Fund at the Ministry of High Education in Jordan for supporting this research. Also, we would to thank CERG team at George Mason University for their valuable supports and HDL resources.
REFERENCES
- A. Moh’d, N. Aslam, H. Marzi and L. A. Tawalbeh, “Hardware Implementations of Secure Hashing Functions on FPGAs for WSNs,” Proceedings of the 3rd International Conference on the Applications of Digital Information and Web Technologies (ICADIWT 2010), Istanbul, 12-14 July 2010.
- “A Guide to Building Secure Web Applications,” 2002. http://www.cgisecurity.com/owasp/html/guide.html
- J.-P. Aumasson, L. Henzen, W. Meier and R. C.-W. Phan, “SHA-3 Proposal BLAKE,” NIST (Round 3), University of California Santa Barbara, Santa Barbara, 2010.
- X. Guo, M. Srivistav, S. Huang, D. Ganta, M. Henry, L. Nazhandali and P. Schaumont, “Silicon Implementation of SHA-3 Finalists: BLAKE, Grøstl, JH, Keccak and Skein,” ECRYPT II Hash Workshop 2011, Tallinn, May 2011.
- P. Gauravaram, L. R. Knudsen, K. Matusiewicz, F. Mendel, C. Rechberger, M. Schläffer and S. S. Thomsen, “Grø- stl—A SHA-3 Candidate,” NIST, University of California Santa Barbara, Santa Barbara, 2011.
- R. Lien, T. Grembowski and K. Gaj, “A 1 Gbit/s Partially Unrolled Architecture of Hash Functions SHA-1 and SHA-512,” CT-RSA 2004, Vol. 2964, 2004, pp. 324-338.
- R. Chaves, G. Kuzmanov, L. A. Sousa and S. Vassiliadis, “Improving SHA-2 Hardware Implementations,” Cryptographic Hardware and Embedded Systems—Ches, Vol. 4249, 2006, pp. 298-310. doi:10.1007/11894063_24
- NIST and FIBS-PUB 180-2, “Secure Hash Standard,” 2002. http://csrc.nist.gov/publications/fips/fips180-2
- R. P. McEvoy, F. M. Crowe, C. C. Murphy and W. P. Marnane, “Optimisation of the SHA-2 Family of Hash Functions on FPGAs,” IEEE Computer Society Annual Symposium on VLSI: Emerging VLSI Technologies and Architectures (ISVLSI 06), IEEE Computer Society, Washington DC, 2006, pp. 317-322.
- M. Feldhofer and C. Rechberger, “A Case against Currently Used Hash Functions in RFID Protocols,” Workshop on RFID Security (IS’06), Graz, 13-14 July 2006, pp. 372-381.
- S. Tillich. “Hardware Implementation of the SHA-3 Candidate Skein,” 2009. http://eprint.iacr.org
- S. Tillich, M. Feldhofer, W. Issovits, T. Kern, H. Kureck, M. Mühlberghuber, G. Neubauer, A. Reiter, A. Köfler and M. Mayrhofer, “Compact Hardware Implementations of the SHA-3 Candidates ARIRANG, BLAKE, Grøstl, and Skein,” 2009. http://eprint.iacr.org/2009/349.pdf
- E. Homsirikamol, M. Rogawski and K. Gaj, “Comparing Hardware Performance of Round 3 SHA-3 Candidates Using Multiple Hardware Architectures in Xilinx and Altera FPGAs,” Encrypt II Hash Workshop—Tallinn, Estonia, 19-20 May 2011.
- E. Homsirikamol, M. Rogawski and K. Gaj, “Comparing Hardware Performance of Round 3 SHA-3 Candidates Using Multiple Hardware Architecture in Xilinx and Altera FPGAs,” CRYPT II Hash Workshop 2011, Tallinn, May 2011.
- X. Guo, M. Srivastav, S. Huang, D. Ganta, M. B. Henry, L. Nazhandali and P. Schaumont, “Silicon Implementation of SHA-3 Finalists: BLAKE, Grøstl, JH, Keccak and Skein,” Center for Embedded Systems for Critical Applications (CESCA) Bradley Department of Electrical and Computer Engineering Virginia Tech, Blacksburg, 2010.
- S. Huang, “Hardware Evaluation of SHA-3 Candidates,” Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, 2011.
- X. Guo, S. Huang, L. Nazhandali and P. Schaumont, “On the Impact of Target Technology in SHA-3 Hardware Benchmark Rankings,” Report 2010/536, IACR Cryptology ePrint Archive, 2010.
- B. Akin, A. Aysu, O. C. Ulusel and E. Savas, “Efficient Hardware Implementation of High Throughput SHA-3 Candidates Keccak, Luffa and Blue Midnight Wish for Singleand Multi-Message Hashing,” Proceedings of the Second SHA-3 Candidate Conference, Santa Barbara, 23- 24 August 2010.
- A. H. Namin and M. A. Hasan, “Implementation of the Compression Function for Selected SHA-3 Candidates on FPGA,” University of Waterloo, Waterloo, 2010.
- X. Guo, S. Huang, L. Nazhandali and P. Schaumont, “Fair and Comprehensive Performance Evaluation of 14 Second Round SHA-3 ASIC Implementations,” Proceedings of the 2nd SHA-3 Candidate Conference, Santa Barbara, 23-24 August 2010.
- NIST, “Cryptographic Hash Algorithm Competition,” 2010. http://csrc.nist.gov
- NIST, “Secure Hashing,” 2011. http://csrc.nist.gov
- X. Y. Wang, et al., “Finding Collisions in the Full SHA- 1,” Proceedings of Crypto, Santa Barbara, 14-18 August 2005, pp. 17-36.
- H. J. Wu, “The Hash Function JH,” NIST (Round 3), 2011.
- G. Bertoni, J. Daemen, M.el Peeters and G. Van Assche, “Keccak Sponge Function Family Main Document,” NIST, University of California Santa Barbara, Santa Barbara, 2009.
- N. Ferguson, S. Lucks, B. Schneier, D. Whiting, M. Bellare, T. Kohno, J. Callas and J. Walker, “The Skein Hash Function Family,” NIST Cryptographic Hash Algorithm Competition, University of California Santa Barbara, Santa Barbara, 2008.

