Journal of Information Security
Vol.3 No.1(2012), Article ID:16723,10 pages DOI:10.4236/jis.2012.31001
Random but System-Wide Unique Unlinkable Parameters
System Security Group, Klagenfurt University, Klagenfurt, Austria
Email: Peter.Schartner@aau.at
Received August 23, 2011; revised October 24, 2011; accepted November 4, 2011
Keywords: Randomness; System-Wide Uniqueness; Unique Cryptographic Parameters; Cryptographic Keys; Digital Identifiers; Digital Pseudonyms; UUID; Universally Unique Identifiers; GUID; Globally Unique Identifiers
ABSTRACT
When initializing cryptographic systems or running cryptographic protocols, the randomness of critical parameters, like keys or key components, is one of the most crucial aspects. But, randomly chosen parameters come with the intrinsic chance of duplicates, which finally may cause cryptographic systems including RSA, ElGamal and Zero-Knowledge proofs to become insecure. When concerning digital identifiers, we need uniqueness in order to correctly identify a specific action or object. Unfortunately we also need randomness here. Without randomness, actions become linkable to each other or to their initiator’s digital identity. So ideally the employed (cryptographic) parameters should fulfill two potentially conflicting requirements simultaneously: randomness and uniqueness. This article proposes an efficient mechanism to provide both attributes at the same time without highly constraining the first one and never violating the second one. After defining five requirements on random number generators and discussing related work, we will describe the core concept of the generation mechanism. Subsequently we will prove the postulated properties (security, randomness, uniqueness, efficiency and privacy protection) and present some application scenarios including systemwide unique parameters, cryptographic keys and components, identifiers and digital pseudonyms.
1. Introduction
Concerning cryptographic parameters, cryptographic keys and digital identifiers, randomness is the foremost requirement. With respect to cryptographic applications, the lack of sufficient randomness causes security risks which may result in faster attacks or completely compromised systems. In the field of digital identifiers, the lack of randomness may cause privacy problems, when identifyers (and hence actions) become linkable to each other or to the identity of a specific instance or person.
Beside the positive effects of randomness mentioned above, random generation processes unavoidably come with the intrinsic risk of duplicates. Unfortunately, these duplicate cryptographic parameters, cryptographic keys and digital identifiers can put the security of safetyor security-critical systems at risk as well.
1.1. The Risks of Pure Randomness
Digital Identifiers: In our everyday electronic life, duplicate parameters used as digital identifiers may cause severe problems. Think of object and message identifiers or digital identities in e-business or e-government applications. In the first case, duplicate identifiers may cause inconsistencies in databases or the system’s registry. In the second case, records of different instances or persons may become inseparably mixed up. Both situations may end up in disaster.
In the context of security systems like RSA encryption and signature schemes, ElGamal signature schemes and zero knowledge proofs, duplicates may cause the following problems (for details on the following attacks we refer the reader to [1,2]):
RSA [3]: Assume that two instances accidentally choose the same prime when generating the RSA key pair. Since this common prime is a factor of both moduli, an attacker can easily determine the second factor of the two affected moduli. Afterwards, he can determine the according private keys. If the key pairs have been used in an encryption scheme, the attacker can now decrypt messages he is not authorized for. In case of a signature scheme, he can sign on the victims’ behalf and hence fake their identities.
ElGamal [4]: If a signing instance signs two different messages using the same randomizer, the attacker can retrieve the private signing key by solving two linear congruencies. Again, the signature scheme is broken.
Zero Knowledge Proofs [5]: Consider two rounds of a zero knowledge proof, where the same first message (based on the same random parameter) is sent to the verifier. If the verifier notices this fact, he will send two different second messages in order to extract the secret by use of the third messages. Again the attacker can now fake the identity of the victim.
1.2. The Problem of Randomness vs Uniqueness
In order to avoid the problems mentioned above, we need random and unique (cryptographic) parameters. Unfortunately, randomness and (system-wide) uniqueness are potentially conflicting requirements. Pure randomness includes the risk of duplicates and hence may violate uniqueness, whereas generation processes which guarantee system-wide uniqueness may reduce randomness or cause the generation to be either inefficient or prone to other attack scenarios.
1.3. Our Contribution
In this article we will propose a solution for the problem of randomness vs. uniqueness: a scheme to generate provably system-wide unique, but highly random and unlinkable numbers (called collision-free numbers—CFNs) which can be used as digital identifiers (or pseudonyms) and cryptographic parameters and keys.
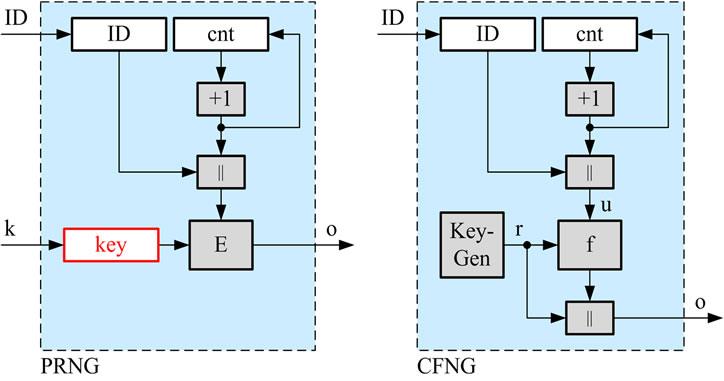
As other approaches, our scheme is based on a unique identifier for the generating process and additional noninvertible (cryptographic) mechanisms to disguise it and hence protect the generator’s privacy. Simply spoken, our approach is a counter-based pseudo-random number generator (PRNG) with a fresh (random) key for each call of the generator (see Figure 6 for a PRNG (left) and our approach (right)). It is clear, that providing both properties at the same time, will not be achievable without extra costs. Based on a short discussion of related work, we will show that this overhead is quite low compared to the existing methods of generation (see Table 1), which in contrast to our approach do not provide randomness and uniqueness simultaneously.
The remainder of this article is structured as follows: In order to provide a base for our design and the subsequent analysis, we will first define five requirements on random number generators and provide the most essential cryptographic preliminaries. Based on the requirements we will briefly discuss existing approaches. The analysis will show that none of the existing generation methods simultaneously fulfills all requirements. Hence there is need for a new approach. After presenting the design principle of CFNGs we will prove the fulfillment of the stated requirements and close with a discussion of application scenarios for CFNGs.
2. Requirements on Random Number Generators
In order to avoid the risks of duplicates when generating and using cryptographic parameters or digital identifiers, we postulated two additional requirements on the employed secure and efficient generators for random numbers in [2]: Uniqueness and Privacy Protection. We called generators providing the following properties collision-free number generators (CFNG) and the outputs of such generators collision-free numbers (CFNs):
1) Security.
2) Randomness.
3) Efficiency.
4) Uniqueness.
5) Privacy Protection.
We are aware of the fact, that depending on the application scenario, not all of the above requirements may be necessary or there may be additional requirements. Nevertheless, in the scope of generating cryptographic parameters (like keys) and digital identifiers, these requirements are necessary to obtain a secure generating process and hence the existing methods of generation and our proposed approach will be analyzed with respect to the five requirements stated above.
2.1. Security
If one CFNG is compromised, all outputs previously generated by this specific generator should remain secure. Additionally, all other CFNGs in the system must not be affected. This means that there should not be a centralized CFNG (since compromising this CFNG immediately compromises the whole system) and distributed CFNGs must not use any common secrets like the secret key k used by the compromised generator G1 in Figure 1.
2.2. Randomness
Ideally, the outputs of CFNGs (see value 2 in Figure 2) are indistinguishable to the outputs of true random number generators (RNG—see value 1 in Figure 2).
In fact, the proposed generators will be based on true random numbers, but will be post-processed to fulfill the newly introduced requirement of uniqueness. Nevertheless, the only way to verify the randomness is to perform statistical tests (like the DIEHARD test suite [6]) on the generated sequences and compare the outputs to the properties of true random sequences.
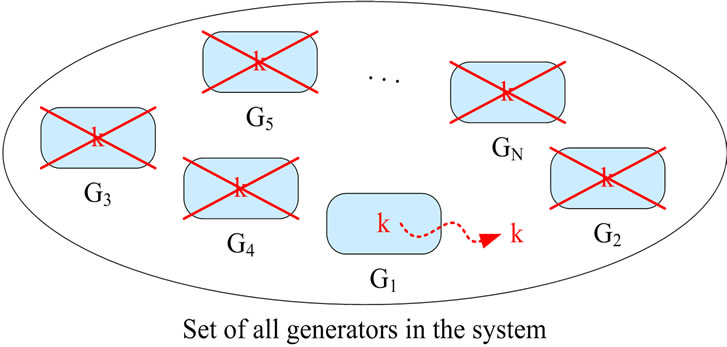
Figure 1. Compromising generator G1 compromises all generators.
2.3. Efficiency
Concerning efficiency, minimal communications is the foremost requirement. Ideally, as depicted in Figure 3, there is no communication during the generation process and only one-time communication during the initializetion. Nevertheless, to enable the usage of smart cards and other security token with limited resources, memory and computational demands should also be kept as low as possible.
2.4. Uniqueness
All outputs of all CFNGs within a system have to be unique, i.e., there must not be any duplicates during the life-time of the system. As depicted in Figure 4, randomly generated values may be system-wide unique (e.g. outputs 1, 2 and 3), locally, but not system-wide unique (e.g. outputs 4 and 5) or not unique at all (e.g. outputs 6 and 7).
Local duplicates may be detected by storing all outputs and comparing the currently generated value against the stored ones. Obviously, this method will need a considerable amount of memory over the life-time of the generator. But even worse, global duplicates cannot be detected without communication with all the other generators or a centralized instance for checking. Besides a tremendous communication overhead, this again calls for local or centralized storage of all outputs for later comparison, which is obviously a bad idea with respect to the requirements “security” and “privacy protection”.
2.5. Privacy Protection
Depending on the application scenario, outputs of CFNGs should not be linkable. As Figure 5 shows, with respect to the protection of the generator’s identity, especially two questions are of interest:
• Which CFNG has generated this (a specific) number?
• Have these numbers been generated by the same CFNG?
3. Cryptographic Preliminaries
Within this article the reader needs only a basic understanding of cryptography. So we will provide the most important facts and refer the reader to [7,8] for a detailed discussion of the basic concepts and more sophisticated cryptographic algorithms and protocols.
Symmetric encryption provides confidentiality. Encryption E and decryption D use the same key k: c = Ek(m), m = Dk(c) with plaintext m and ciphertext c. Without the knowledge of k, m cannot be efficiently retrieved from c. Most commonly, symmetric encryption algorithms are block-oriented, i.e., they work on input blocks of fixed length. Candidates for symmetric encrypt
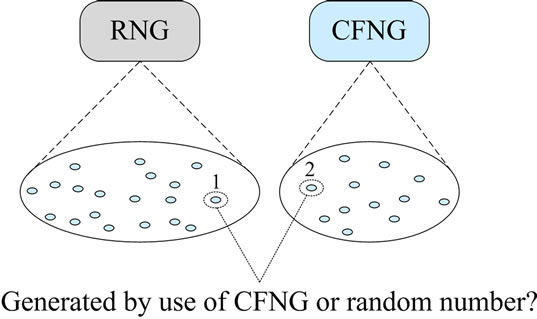
Figure 2. Outputs of a RNG and a CFNG.
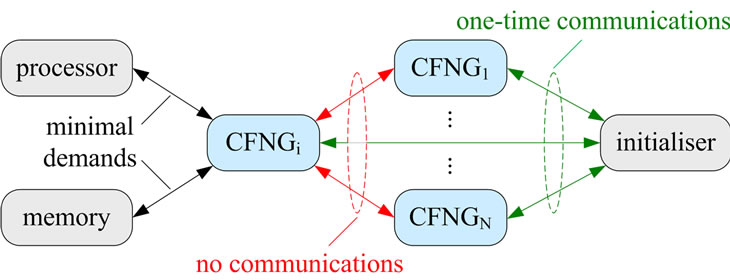
Figure 3. Efficiency considerations.
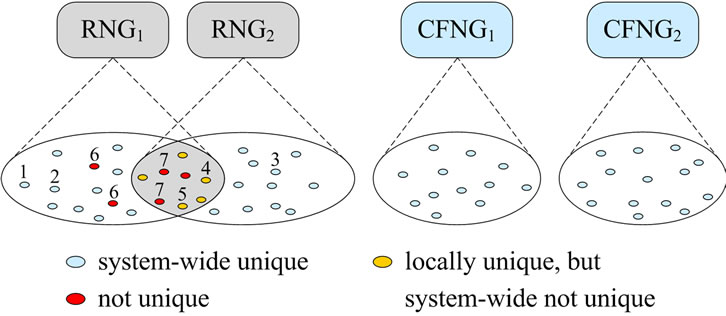
Figure 4. Outputs of RNGs and CFNGs.
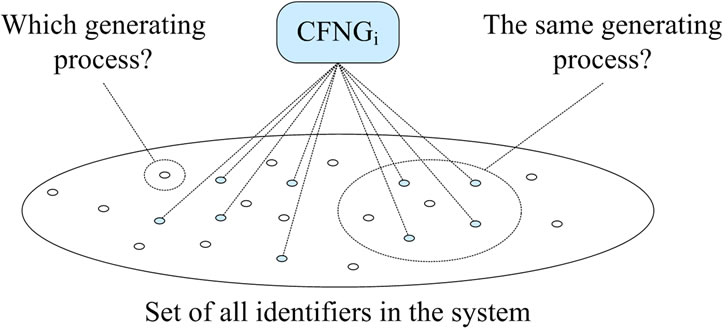
Figure 5. Privacy protection.
tion include DES [9] (Data Encryption Standard, 64 bit blocks and 56 bit keys), 3DES [10,11] (64 bit blocks and 112 bit keys), Skipjack [12] (64 bit blocks and 80 bit keys) and AES [13] (Advanced Encryption Standard, 128 bit blocks and 128,192 and 256 bit keys).
Asymmetric encryption also provides confidentiality, but uses different keys for encryption and decryption: c = Ee(m), with public key e and m = Dd(c), with private key d. Without knowing d, m cannot be efficiently retrieved from c, and d cannot be efficiently derived from e without additional (secret) knowledge. Candidates for asymmetric encryption include RSA [3] and ElGamal [4] (minimum key length 1024 bit) and ECC [8] (Elliptic Curve Cryptography, minimum key length 160 bit).
Cryptographic Hash-functions H are compressing one-way-functions, which convert a large, arbitrary sized input m into a small, fixed size hash value h (most commonly 128 or 160 bit): h = H(m). Candidates for Hashfunctions include SHA-1 [14] and RIPEMD160 [15], both with 160 bit outputs and the SHA-2 family [16] (224 to 512 bit outputs). Note that both, symmetric and asymmetric encryption and decryption functions are bijective for an arbitrary, but fixed key, whereas hashfunctions are by definition not injective!
4. Related Work
There exist at least three straight forward solutions for generating random and system-wide unique parameters:
The naive attempt of centralized generation and check obviously avoids duplicates but is quite inefficient concerning storage (all previously generated parameters have to be stored for later comparison) and communication (each instance which needs a parameter has to wait for the centralized generator to send it). Additionally, the centralized generator has full control over the generating process and knows all parameters. So, compromising this generator compromises the complete system.
With local generation and check, only the generation itself is done locally, but the comparison against all previously generated parameters has to involve all other generators or a centralized service. Again, efficiency and security are quite questionable.
Local generation based on pseudo-random number generators (PRNG, see [7]) can avoid centralized storage and comparison and is efficient in terms of memory and communications. But in order to avoid duplicates, all PRNGs have to use a common key or common secret parameters. So, if one of them is compromised, all of them become insecure. Additionally, the generated parameters are no longer random, but pseudo-random and this approach is not suitable for software implementation, because by use of software, the system-wide key (or secret parameter) cannot be protected sufficiently.
A more sophisticated approach is the so called locationand time-based generation which simply uses location and time provided by a GPS receiver to derive a unique seed for the generation process. The idea behind this concept: two generation processes cannot take place at the same place and the same time. Besides the fact that the GPS signal will not be available at all locations, the according paper does not specify, how (pseudo-) randomness and uniqueness are maintained (see [17] for details).
A widely adopted approach for system-wide unique system parameters are universally unique identifiers (UUIDs, see [18]) and globally unique identifiers (GUIDs, see [19]), Microsoft’s implementation of GUIDs. There exist several variants of GUIDs, but these variants either use the MAC address to guarantee uniqueness or they employ hash-functions or purely pseudo-random values. Except the first one, which violates the privacy requirement, none of them can guarantee uniqueness.
Besides the attempts mentioned above, there exist some national methods for the generation of identifiers used in e-business and e-government processes. Again, these methods employ hash-functions to protect the identity of the generating process and come with the unavoidable risk of duplicates (e.g. see [20]).
Table 1 shows a summary of the discussed related work according the requirements stated in Section 2. Here “-” denotes, that the described generation method lacks a certain property, “??” denotes that it is unclear whether a generator provides a specific property (according to the publicly available specification) and “ok” denotes that the generator provides the property.
Note that none of the existing approaches shows “ok” for all five requirements. The analysis of our approach (see Section 6) will show that CFNGs (collision-free number generators) fulfill all requirements.
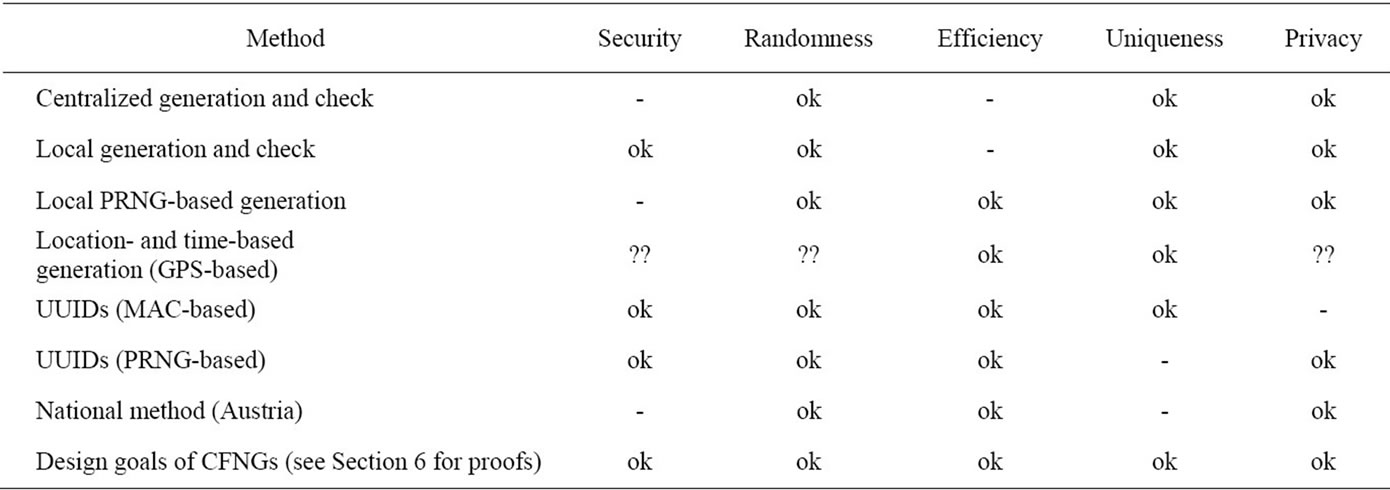
Table 1. Related work—a short analysis and comparison.
5. The Concept of Collision-Free Numbers
The core concept of collision-free number generators (CFNG) is closely related to pseudo-random number generators based on the CTR-mode of block-ciphers which uses a random but fixed key k throughout its lifetime (see Figure 6(a)). The crucial difference of CFNGs compared to a PRNG in CTR-mode is that the key used by the CFNG is freshly chosen at random for each call of the generator (see Figure 6(b)).
Informally, our approach is based on three facts:
• Use counters that generate system-wide unique outputs u. This can easily be achieved by using counters of the following form: u = ID||cnt, where ID is a hierarchically structured identifier (e.g. the ICCSN of a smartcard), unique for each generator, and cnt is a locally stored value, which is incremented before each call of the generator.
• Employ some injective mixing function 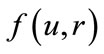 which hides the value of u by use of a so called randomizer r. This randomizer is freshly chosen at random for each call of the generator and deleted immediately after usage.
which hides the value of u by use of a so called randomizer r. This randomizer is freshly chosen at random for each call of the generator and deleted immediately after usage.
• In order to fix the uniqueness, embed the randomizer r in the output o of the generator by use of an injective bit permutation (or expansion). For the ease of discussion, we will use the concatenation (||) throughout the remainder of this article.
More formally defined, the output o of a basic—type 1—CFNG (denoted as CFNG1 in the remainder of this article) is of the form
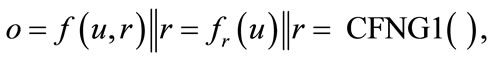
with f being an injective mixing transformation for an arbitrary but fixed randomizer r and u, r defined as above. We suggest to either use an injective one-way mixing-transformation for fr, according to Shannon [21] (e.g. symmetric encryption), or an injective probabilistic oneway function, based on an intractable problem (e.g. the discrete logarithm problem [7]).
 (a) (b)
(a) (b)
Figure 6. Block-cipher in CTR-mode and the concept of CFNG (type 1).
Note that originally, CFNGs have been called quasirandom number generators (QRNG). Since our generators provide numbers being neither pseudo-random nor random, QRNG—alphabetically and concerning the outputs being somewhat between PRNGs and true RNGs— would be the perfect name. Unfortunately the abbreviation QRNG collides with generators for quasi random sequences used for statistical testing. Hence to avoid this duplicate, we changed the name to CFNG.
6. Fulfillment of Requirements
6.1. Security
In our approach, all security critical parameters like randomizers or keys are nonces (numbers used once) generated on demand, i.e., at each call of the generator. They are neither stored, nor transferred outside the generator. Hence, compromising one generator cannot affect any other generator in the system.
6.2. Uniqueness
In the following we will first give a proof for the uniqueness of outputs of Type 1 CFNGs. Based on this proof we will analyze Type 2 and Type 3 generators. Note that the lifetime of the system and especially of the generators employed within this system is defined by the time, none of the counters cnt used inside of the CFNGs has an overflow.
Theorem: Outputs of Type 1 CFNGs are unique during their lifetime.
Proof: Consider two outputs of two arbitrary type 1 CFNGs: 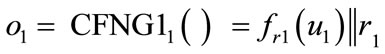 and
and 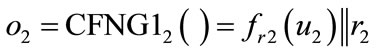 , with r1, r2 being random and
, with r1, r2 being random and 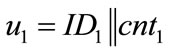 and
and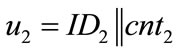 . With respect to the randomizers r1 and r2, there are two cases:
. With respect to the randomizers r1 and r2, there are two cases:
1)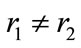 : This directly means that o1 ≠ o2.
: This directly means that o1 ≠ o2.
2)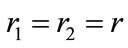 : Now, both calls of the generators employ the same randomizer and fr becomes injective. Hence
: Now, both calls of the generators employ the same randomizer and fr becomes injective. Hence  and
and  will be different if and only if
will be different if and only if 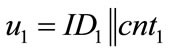 and
and 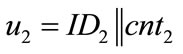 differ in at least one bit. This is always true, because
differ in at least one bit. This is always true, because
• Different generators use different identifiers 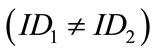 , and
, and
• If we call the same generator twice (i.e.,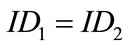 ), the values cnt1 and cnt2 will differ, because the counter is incremented at each call of the generator.
), the values cnt1 and cnt2 will differ, because the counter is incremented at each call of the generator.
Hence the outputs o1 and o2 will be different again. 
Corollary: Outputs of type 2 and type 3 CFNGs are unique during their lifetime.
Proof: Function g, applied to the unique inputs in type 2 and type 3 CFNGs is an injective one-way-function. Hence g cannot destroy the uniqueness of the outputs. 
6.3. Privacy Protection
When analyzing CFNGs which employ a block cipher E for f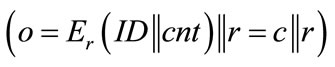 , it is obvious that the identity of the generator is not protected sufficiently. Everybody who gets hold of an output o can retrieve the identifier ID of the according generator by simply decrypting c by use of r:
, it is obvious that the identity of the generator is not protected sufficiently. Everybody who gets hold of an output o can retrieve the identifier ID of the according generator by simply decrypting c by use of r: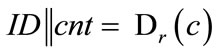 . We will later see that this may not be a problem in certain application scenarios, but in order to guarantee the protection of the generator’s ID we have either to change our requirements on f, or we have to slightly change the design of CFNGs.
. We will later see that this may not be a problem in certain application scenarios, but in order to guarantee the protection of the generator’s ID we have either to change our requirements on f, or we have to slightly change the design of CFNGs.
• To provide privacy, f has to be a cryptographic oneway function. Candidates include injective probabilistic one-way functions based on an intractable problem like the (ECC) discrete logarithm problem [7].
• In the case that f is a (bijective) symmetric encryption function, we can employ an additional (injective) oneway-function g to the output or to the randomizer of the original CFNG, which results in the variants depicted in Figure 7.
Both variants shown in Figure 7 eliminate the attack described above. Now the attacker is faced with the problem of inverting function g, which is practically impossible. Hence, the output of function f in case of type 2 CFNGs, and the randomizer r in case of type 3 CFNGs, stays secure and the identity of the generator is safe again.
6.4. Randomness
Remember that in case of type 1 CFNGs, the second half of the output is the randomizer, which is—as the name implies—generated at random. Function f is (with respect to the random input r) an injective mixing transformation, like a symmetric or asymmetric encryption function. Hence its output is pseudo-random.
Function g, applied in type 2 and type 3 CFNGs is a (injective) one-way-function. The randomness of its output depends on the randomness of its input, which is either the pseudo-random output of f (type 2 CFNG), or the randomizer r (type 3 CFNG).
Concerning the randomness of the outputs, we will briefly analyze the three types of CFNGs separately:
Type 1 CFNGs: The output is a concatenation of pseudo-random and random bits, and hence should “look random”.
Type 2 CFNGs: The input of function g is, as noted above, partially pseudo-random and random. So, the randomness of type 2 CFNGs should not be worse than the randomness of type 1 CFNGs.
Type 3 CFNGs: The output is a concatenation of pseudo-random and random bits, transformed by use of function g. So again, the output should “look random”.
For all three types of generators, the statement “should look random” has been verified by conducting statistical tests with the DIEHARD test suite [6]. See Table 3 for exemplary DIEHARD results on 500.000 outputs o of a type 1 CFNG (i.e., 128.000.000 bit) of the form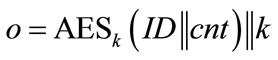 , where ID is a 96 bit identifier (all zeros), cnt is a 32 bit counter (which runs from 0 to 499.999) and k is a 128 bit key randomly chosen for each encryption. Hence the length of one output o is 256 bit. According to [22] we defined three areas: safe, doubtful, and failure, (see Table 2) where more results in the safe area indicate that the output is closer to randomness and more results in the failure area indicate that the tested sequence deviates from true randomness.
, where ID is a 96 bit identifier (all zeros), cnt is a 32 bit counter (which runs from 0 to 499.999) and k is a 128 bit key randomly chosen for each encryption. Hence the length of one output o is 256 bit. According to [22] we defined three areas: safe, doubtful, and failure, (see Table 2) where more results in the safe area indicate that the output is closer to randomness and more results in the failure area indicate that the tested sequence deviates from true randomness.
Analyzing Table 3 with respect to the areas failure, doubt and safe we get 8, 13 and 26 entries, which is (as expected) quite close to the output of AES encrypted data (see [22]). Note that other test outputs and generators might have different outcomes, but this analysis of outputs of type 1 CFNGs strongly supports our brief theoretical analysis given above: the outputs “look random”.
6.5. Efficiency
Our system is very effective with respect to communications. The only time we need to interact with a generator is during initialization, where the unique identifier ID is loaded into the generator’s memory. After that, especially during the generation of CFNs, there is no need for any communication at all.
Concerning the computation of CFNs, the approach is

Table 2. Interpretation of DIEHARD p-values: safe—doubt—failure.
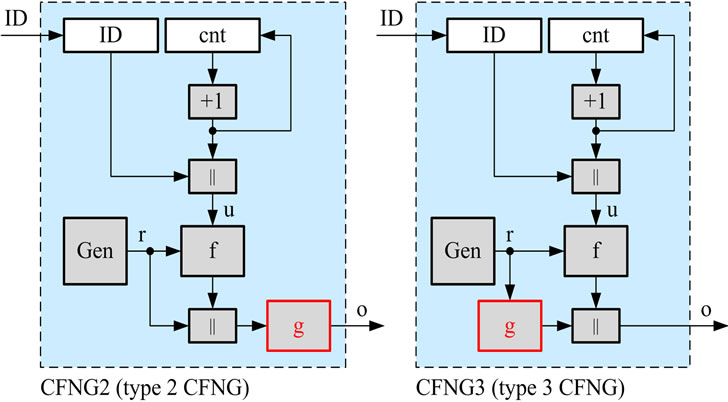
Figure 7.Variants of CFNGs ensuring privacy protection.
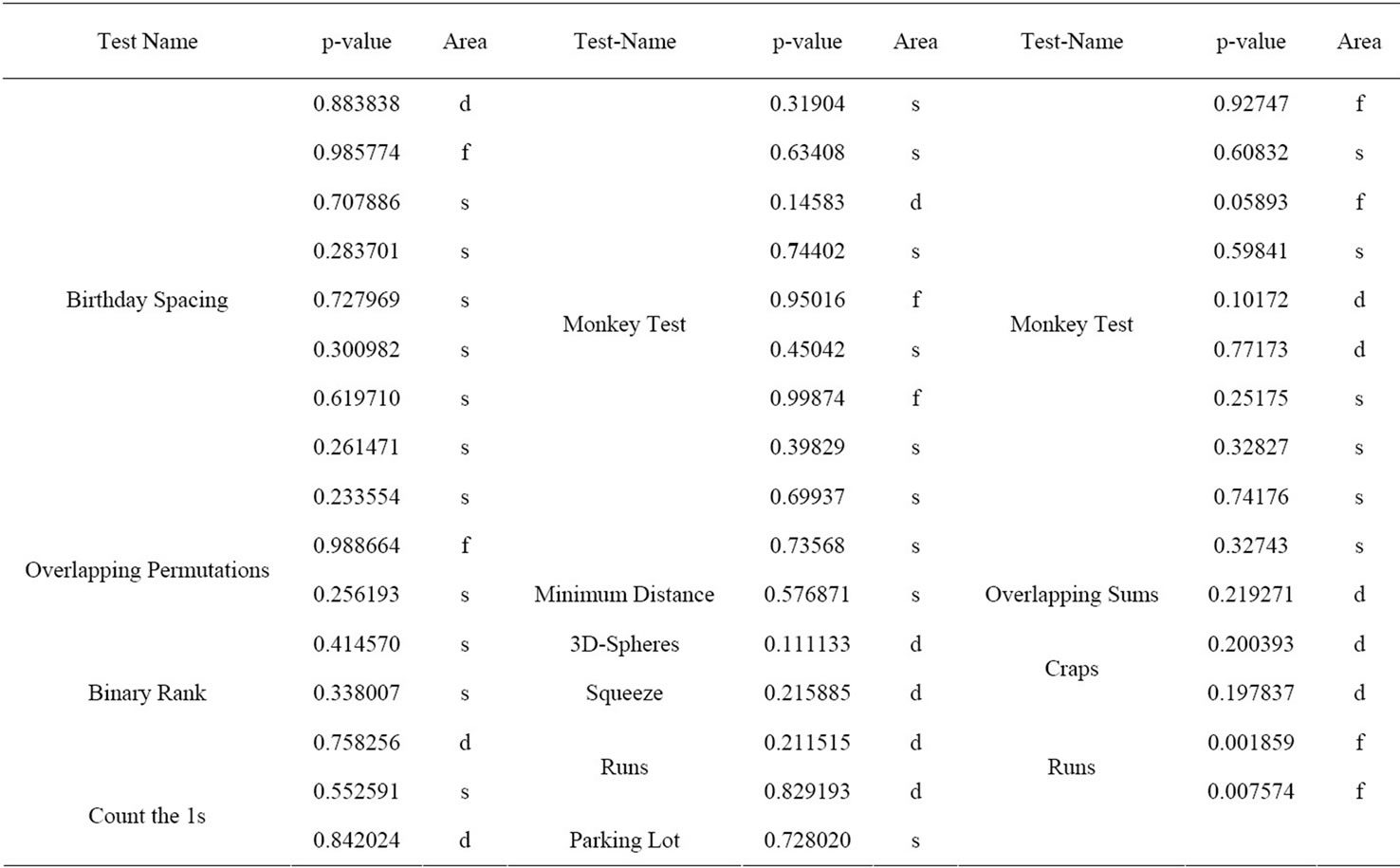
Table 3. DIEHARD test on type 1 CFNGs.
quite efficient, as well. See Table 4 for a summary of different variants of type 1 CFNGs and Table 5 for detailed timings of the CFNGs implemented in software on a SmartCafe Expert 2.0 JavaCard (see [23] and [24] for more details on the implementation of CFNGs). In case of Type 2 CFNGs, we used two different approaches to implement function g: elliptic curve scalar multiplication (SM) and modular exponentiation (ME).
As far as memory is concerned, each generator needs to locally store its ID and the current value of the counter cnt. One may argue that compared to true random numbers or pseudo-random numbers, CFNs are quite long. The following comparison—which clarifies that CFNGs are worth consideration—is based on generating 2n numbers of bit-length N by use of RNGs, CFNGs, and PRNGs:
RNG: Remembering the birthday paradox, you will have a fair chance (~50%) to get a duplicate after generating approximately 2N/2 values (of bit-length N). Of course, keeping slightly below 2N/2 values will significantly reduce the probability of duplicates, but no matter how many outputs you generate, you cannot completely eliminate the risk of duplicates. In the worst case scenario, the second value generated is the first duplicate!
CFNG: Now think of CFNGs which generate the same number of CFNs. When employing a block cipher E for f,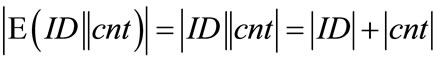 . If
. If 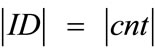 = N/4, the length of r results in |r| = N/2. With this setup, the
= N/4, the length of r results in |r| = N/2. With this setup, the

Table 4. Comparison of softwareand hardware-based CFNGs.
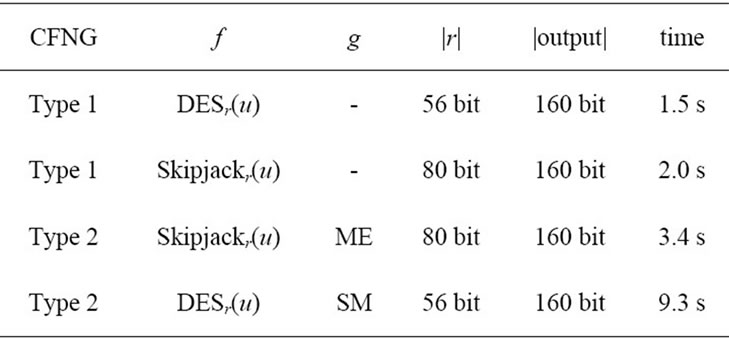
Table 5. Time for generating a CFN.
2N/4 generators in our system can generate 2N/4 outputs each, without any collisions. Note that if you need more generators and less outputs per generator, simply shift some bits from cnt to ID (i.e., increase the length of ID and decrease the length of cnt) and vice versa. As long as 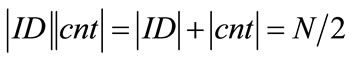 you will not get any duplicates when generating 2N/2 values.
you will not get any duplicates when generating 2N/2 values.
PRNG: Obviously, PRNGs which use a common secret key and hierarchically structured counters can generate 2N unique outputs of size N without any duplicates. Nevertheless, since compromising one means compromising all, PRNGs are no option here.
Note that employing cryptographic mechanisms like hash-functions or encryption always slows down the generation process. But, when we want to protect the privacy of the generator’s identity, the use of cryptographic primitives is mandatory. Modern smartcard microprocessors (like SmartCafe Expert 5.0 JavaCard from Giesecke and Devrient [25]) and modern CPUs (like Intels Westmere-based and Sandy Bridge processors [26]) provide encryption functions (like AES) implemented in hardware, but most commonly only provide software-based hash-functions.
Practical test on a SmartCafe Expert 5.0 JavaCards from Giesecke and Devrient [25] showed that hardwarebased encryption is two to four times faster than hardware based hashing of the same data, and 10 to 15 times faster than hashing by use of software [27]. Hence, compared to the existing solutions like UUIDs or GUIDs which use hash-functions, our approach which uses encryption is quite competitive.
7. Fields of Application
Originally, CFNGs have been designed to eliminate the attack scenarios, briefly described in the introduction of this article. Besides that, we discovered that the concept of CFNGs could be quite useful in the field of unique identifiers as well. Additionally, by changing from symmetric to asymmetric algorithms, CFNGs can be used to generate unique pseudonyms, which can directly be used as keys in cryptographic protocols.
7.1. Unique Cryptographic Parameters and Keys
Reconsidering the attacks in Section 1.1 we will first describe how CFNGs will fix the problems with randomness in cryptographic protocols. Simply spoken, we will replace random parameters by system-wide unique but random parameters, generated by the use of applicationspecific CFNGs.
Primes: The security of an RSA scheme (used for encryption or digital signature) is based on the factorization problem, or more precisely, on the problem of factoring the modulus n which is the product of two random primes: n = pq. If the randomness in the prime generation process is based on CFNGs, there will be no duplicates and no attacks based on common primes. Note that the attacker knows only n, so we have implicit privacy protection here. As a consequence we can use a type 1 CFNG with f being a symmetric encryption algorithm. So the primes will be of the following form:
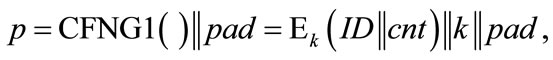
where pad is a sequence of random padding bits which ensures the required length (512 bit upwards). Padding the unique header simplifies the prime generation process. In a first step, we set the least significant bit of p to 1, so that p is an odd number. If p is not prime, we can now simply add 2 and check again. This will be repeated until p is prime. As long as this repeated adding 2 does not interfere with the unique header, our resulting prime will be unique.
ElGamal Randomizers: When using the ElGamal signature scheme, we need some random parameter r, called randomizer, to digitally sign a message. As above, this randomizer is protected by an intractable problem, the discrete logarithm problem. So, we can again use a type 1 CFNG to generate our randomizers:
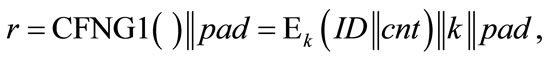
where the padding bit sequence pad can be omitted, if 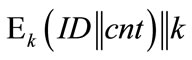 is of sufficient length.
is of sufficient length.
Nonces: Random numbers used once (nonces) are essential for the security of zero knowledge protocols (ZKP). So again, we employ a CFNG to generate the nonces s. Unfortunately, many ZKPs include messages that contain the nonce in unprotected form, or messages of a protocol round can be used to extract the nonce. Hence, to provide explicit privacy protection, we have to use a type 2 or type 3 CFNG:
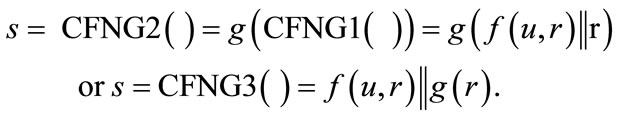
7.2. Unique Identifiers and Pseudonyms
In specific scenarios, we do not care about the privacy protection of the generators identity. In this case, simply employ a type 1 CFNG based on symmetric encryption and where necessary, (randomly) pad the output to the appropriate length.
However, in the majority of cases, digital identifiers and digital pseudonyms (of the same generator) should be unlinkable to each other. This means that we have to provide privacy protection for the identifier, embedded in the CFNGs. So we can either use a type 1 CFNG with a one-way function f or a type 2 or type 3 CFNG.
To explain the operating principle, we will first discuss an RSA-based type 1 generator of the form:
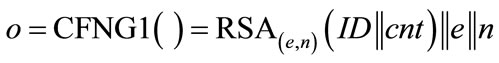
where e is the public exponent of the RSA system and n is the modulus. Although being quite long (|n| ≥ 1024 bit), these identifiers contain a public key (e,n) which can be used to 1) Authenticate the holder of the identifier by verifying his digital signature or to 2) Send encrypted messages to the holder of the identifier, provided that the holder has stored the according private key.
Figure 8 shows the usage of digital pseudonyms in the context of an authentication scheme based on digital signatures. The prover employs an RSA-based type 1 CFNG to generate his unique digital pseudonym  . After the generation, P sends o to the verifier. The verifier extracts the public key (e, n) and sends a challenge r to the prover. The prover signs the challenge and sends the signature s to the verifier, who finally verifies the signature with the public key of the prover.
. After the generation, P sends o to the verifier. The verifier extracts the public key (e, n) and sends a challenge r to the prover. The prover signs the challenge and sends the signature s to the verifier, who finally verifies the signature with the public key of the prover.
In order to keep the identifiers as short as possible, but also protect the identity of the generator, we suggest to use CFNGs of type 2 or type 3 based on elliptic curve cryptography (ECC), elliptic curve scalar multiplication (SM) and point compression (PC). Generators with the shortest outputs, but still secure and privacy protecting are of the form:

where P is a so-called generator point of the elliptic curve (see [8] for details on ECC). By using this type of generator we can achieve outputs with a length form 128 bit upwards. Scenarios which only need short-term security may use 128 bit outputs, but the long-term security requires 160 bit or more. Since the output of the elliptic curve scalar multiplication (SM) is an ECC public keythe key (e,d) with public key , P) and private ECC key
, P) and private ECC key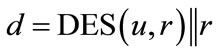 , can be used as sketched above. For a detailed discussion of ECC-based pseudonyms we refer the reader to [28].
, can be used as sketched above. For a detailed discussion of ECC-based pseudonyms we refer the reader to [28].
Finally, when replacing DES by Skipjack (SJ) with CBC mode and ciphertext stealing, these ECC-based type 2 CFNGs (see Figure 9 and [29]) are a secure and efficient replacement for UUIDs which fulfills all requirements on UUIDs (universally unique identifiers). In particular, the generated identifiers, which are based on 48 bit user identifiers (UI), are system-wide (or in UUID’s language universally) unique, whereas UUIDs are not!
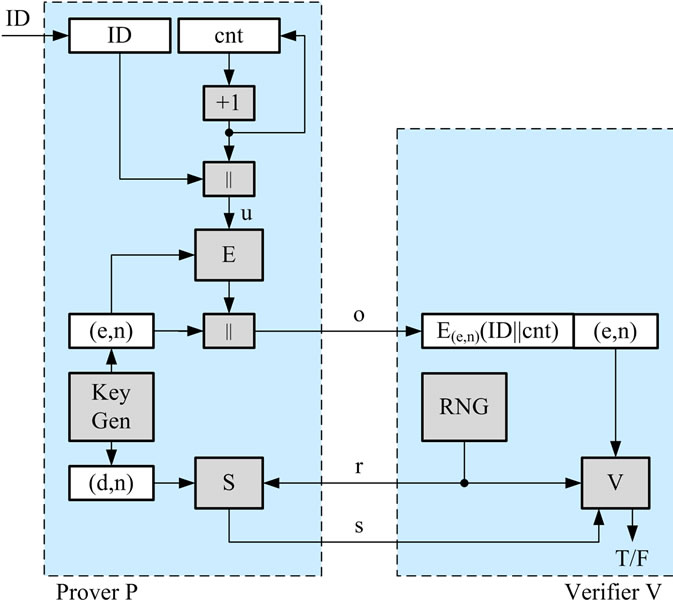
Figure 8. Usage of digital pseudonyms.
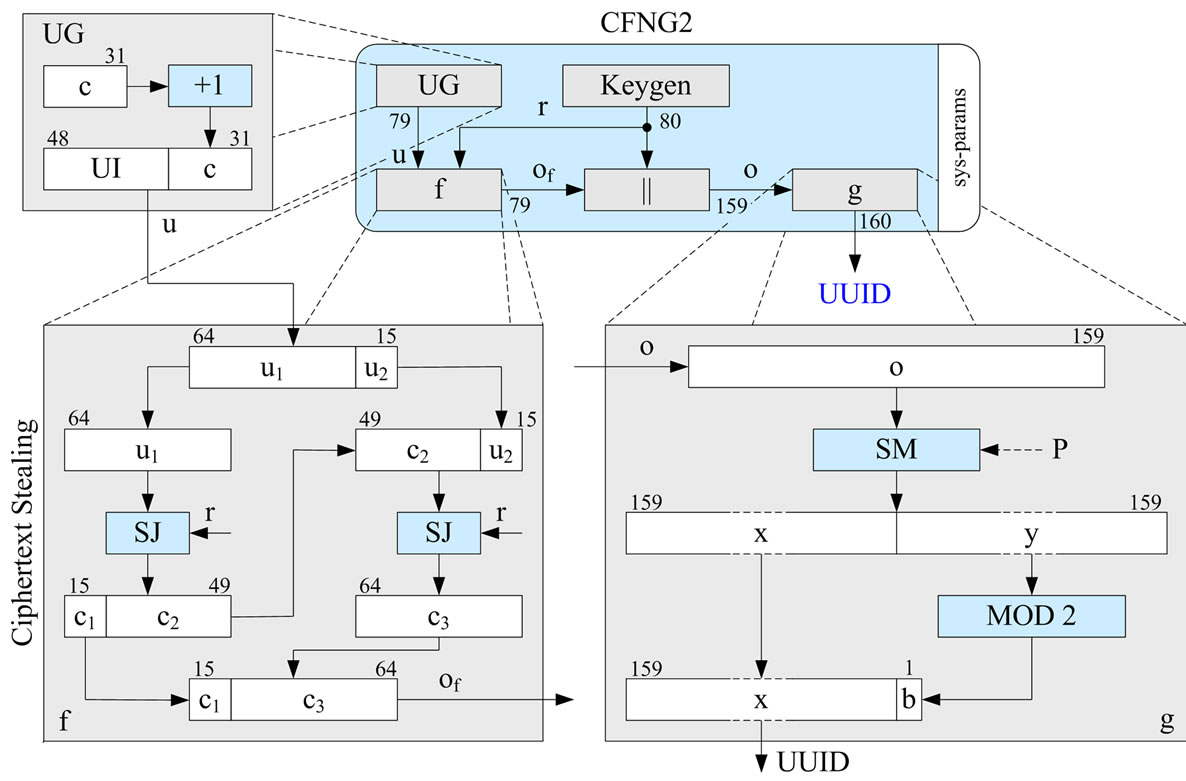
Figure 9. Prototypical Implementation of a type 2 CFNG (160 bit output).
8. Conclusion
Security critical parameters and identifiers, chosen purely random, come with the intrinsic risk of duplicates. These duplicates may cause severe problems in cryptographic schemes, cryptographic protocols and applications. In this article, we proposed an efficient mechanism which could replace true random number generators in the mentioned fields of application. In contrast to true random number generators, the so called collision-free number generators (CFNGs) provably do not generate any duplicates during their life-time. Nevertheless, the proposed generators are secure (compromising one or more generators does not compromise the whole system), efficient (in terms of computation, communications and memory) and they additionally protect the generator’s identity (i.e., outputs are unlinkable to each other and the generator’s identity).
REFERENCES
- P. Schartner, “Security Tokens—Basics, Applications, Management, and Infrastructures,” IT-Verlag, Sauerlach, 2001.
- M. Schaffer, P. Schartner and S. Rass, “Universally Unique Identifiers: How to Ensure Uniqueness While Protecting the Issuer’s Privacy,” Proceedings of Security and Management 2007, CSREA Press, Las Vegas, 2007, pp. 198-204.
- R. L. Rivest, A. Shamir and L. Adleman, “A Method for Obtaining Digital Signatures and Public-Key Cryptosystems,” Communications of the ACM, Vol. 21, No. 2, 1978, pp. 120-126. doi:10.1145/359340.359342
- T. ElGamal, “A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms,” IEEE Transactions of Information Theory, Vol. IT-31, No. 4, 1985, pp. 469- 472. doi:10.1109/TIT.1985.1057074
- S. Goldwasser, S. Micali and C. Rackoff, “The Knowledge Complexity of Interactive Proof Systems,” SIAM Journal on Computing, Vol. 18, No. 1, 1989, pp. 186- 208. doi:10.1137/0218012
- G. Marsaglia, “The DIEHARD Test Suite 2003,” 2003.
- A. J. Menezes, S. A. Vanstone and P. C. Van Oorschot, “Handbook of Applied Cryptography,” CRC Press, London, 1996.
- D. Hankerson, A. J. Menezes and S. A. Vanstone, “Guide to Elliptic Curve Cryptography,” Springer-Verlag, Berlin, 2004.
- National Institute of Standards and Technology—NIST, “FIPS Publication 46-3: Data Encryption Standard (DES),” NIST, Gaithersburg, 1999.
- NIST, “FIPS Special Publication 800-38A: Recommendation for Block Cipher Modes of Operation—Methods and Techniques,” NIST, Gaithersburg, 2001.
- ISO/IEC, “ISO/IEC 10116: Modes of Operation of an n-bit Block Cipher,” 1991. http://www.iso.org
- NIST, “SKIPJACK and KEA Algorithm Specifications,” NIST, Gaithersburg, ver. 2.29, 1998.
- NIST, “FIPS Publication 197: Advanced Encryption Standard (AES),” NIST, Gaithersburg, 2001.
- NIST, “FIPS Publication 180-1: Secure Hash Standard (SHA),” NIST, Gaithersburg, 1995.
- H. Dobbertin, A. Bosselaers and B. Preneel, “RIPEMD- 160: A Strengthened Version of RIPEMD,” Proceedings of Fast Software Encryption (FSE), LNCS, Springer, Berlin, Vol. 1039, 1996, pp. 71-82.
- NIST, “FIPS Publication 180-2: Secure Hash Standard,” NIST, Gaithersburg, 2002.
- IPCOM, “Method of Generating Unique Quasi-Random Numbers as a Function of Time and Space,” PriorArtDatbase, IPCOM#000007118D, 2002.
- P. Leach, M. Mealling and R. Salz, “RFC 4122: A Universally Unique IDentifier (UUID) URN Name-Space,” 2005. http://www.ietf.org/rfc/rfc4122.txt
- Microsoft Developer Network, “Globally Unique Identifiers (GUIDs),” 2008. http://msdn.microsoft.com/en-us/librarycc246025.aspx
- Republik Österreich, “Bundesgesetz über Regelungen zur Erleichterung des Elektronischen Verkehrs mit Öffentlichen Stellen (E-Government-Gesetz—E-GovG),” BGBl. I 10/2004, 2010. http://www.ris.bka.gv.at
- C. E. Shannon, “Communication Theory of Secrecy Systems,” Bell System Technical Journal, Vol. 28, No. 4, 1949, pp. 656-715.
- M. Alani, “Testing Randomness in Ciphertext of BlockCiphers using DIEHARD,” International Journal of Computer Science and Network Security—IJCSNS, Vol. 10, No. 4, 2010, pp. 53-57.
- M. Schaffer, P. Schartner and S. Rass, “Efficient Generation of Unique Numbers for Secure Applications,” Technical Report TR-Syssec-07-01, Klagenfurt University, System Security Group, Klagenfurt, 2007.
- P. Schartner and M. Schaffer, “Implementing CollisionFree Number Generators on JavaCards,” Technical Report TR-Syssec-07-03, Klagenfurt University, System Security Group Klagenfurt, 2007.
- Giesecke and Devrient, “Sm@rtCafe JavaCards,” 2011. http://www.gi-de.com.
- Intel, “Intel Processors Supporting AES-NI,” 2011. http://www.intel.com.
- P. Schartner, “A Low-Cost Alternative for OAEP,” Proceedings of International Workshop on Security and Dependability for Resource Constrained Embedded Systems SD4RCES, ICPS Series, ACM Digital Library, in Print, 2011.
- P. Schartner and M. Schaffer, “Efficient Privacy-Enhancing Techniques for Medical Databases, BIOSTEC, Communications in Computer and Information Science, Springer, Berlin, Vol. 25, 2008, pp. 467-478.
- P. Schartner, “Unique Domain-Specific Citizen Identification for E-Government Applications,” Proceedings of the 6th International Conference on Digital Society— ICDS 2012, Valencia, 30 January-4 February 2011.

