Materials Sciences and Applications
Vol.07 No.12(2016), Article ID:72697,20 pages
10.4236/msa.2016.712062
Thermomechanical Behavior Modeling of a Cr-Ni-Mo-Mn-N Austenitic Stainless Steel
Rafael P. Ferreira1, Eden S. Silva1,2, Carmem C. F. Nascimento1, Samuel F. Rodrigues1,3*, Clodualdo Aranas Jr.3, Valdemar S. Leal1, Gedeon S. Reis1
1Graduate Program in Materials Engineering, Federal Institute of Education, Science and Technology of Maranhão―IFMA, São Luís, MA, Brazil
2Engineering Coordination, Universidade UNICEUMA, São Luís, MA, Brazil
3Department of Materials Engineering, McGill University, Montreal, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 31, 2016; Accepted: December 10, 2016; Published: December 13, 2016
ABSTRACT
The analytical approach and the thermomechanical behavior of a Cr-Ni-Mo-Mn-N austenitic stainless steel were characterized based on the parameters of work hardening (h), dynamic recovery (r) and dynamic recrystallization (n, t0.5), considering constitutive equations (σ, ɛ) and deformation conditions expressed according to the Zener-Hollomon parameter (Z). The results indicated that the curves were affected by the deformation conditions and that the stress levels increased with Z under high work hardening rates. The σc/σp ratio was relatively high in the first part of the curves, indicating that softening was promoted by intense dynamic recovery (DRV). This was corroborated by the high values of r and average stacking fault energy, γsfe = 66.86 mJ/m2, which facilitated the thermally activated mechanisms, increasing the effectiveness of DRV and delaying the onset of dynamic recrystallization (DRX). The second part of the curves indicates that there was a delay in the kinetics of dynamic softening, with a higher value of t0.5 and lower values of the Avrami exponent (n) due to the competing DRV-DRX mechanisms, and steady state stress (σss) was achieved under higher rates of deformation.
Keywords:
Austenitic Stainless Steel, Dynamic Recovery, Dynamic Recrystallization

1. Introduction
Stainless steels combine good mechanical properties, corrosion resistance and good weldability, which are characteristics required in many applications in the chemical, petrochemical and energy industries [1] . The basic composition Fe-Cr-Ni comprises essentially four types of characteristic microstructures: martensitic, ferritic, austenitic and duplex [2] . In industrial settings, these alloys undergo specific hot forming processes in thermomechanical processing, such as rolling and forging, for the manufacture of tubes, plates, valves, hospital equipment, and numerous other applications.
The literature describes the influence of alloying elements (Mo, Ni, N, Mn) on the chemical composition and stacking fault energy (SFE) of stainless steels, and therefore, on thermally activated phenomena [3] . Austenitic steels usually have low SFE. For example, the SFE of AISI 304L steel is 18 mJ/m2, while that of AISI 305 steel is about 34 mJ/m2 and that of AISI 316LVM steel is 78 mJ/m2 [4] . Therefore, given the low SFE of the matrix, the main recovery process in hot deformation is dynamic recrystallization (DRX) [5] . However, the predominant behavior of materials with average SFE is dynamic recovery (DRV), with inhibition of thermally activated phenomena [6] . Thus the kinetics of dynamic softening is characterized by the competing mechanisms of work hardening, DRV and DRX, which give rise to mechanical and microstructural changes.
2. Background
During thermomechanical processing, stainless steels with austenitic structure and low SFE tend to soften by DRX, after reaching a certain degree of deformation [7] [8] [9] . This threshold deformation, known as critical strain (εc), corresponds to the minimum strain required for the onset of DRX, at which the stress is called critical stress (σc) [7] . This value corresponds to the upper limit of the amount of energy that can be stored locally in this type of hot deformed material. However, the critical amount of stored energy alone does not suffice for the onset of DRX, which also requires the energy dissipation rate to reach a critical value. Poliak and Jonas [9] , who applied the principle of thermodynamic irreversibility, determined that the critical condition for the onset of DRX occurs when:
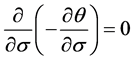 (1)
(1)
where θ represents the work hardening rate. The values of θ can be obtained by calculating the derivative of the experimentally measured σ vs. ε curve, Equation (2):
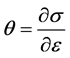 (2)
(2)
In the physical simulation of thermomechanical processing, the occurrence of DRX in materials with low SFE leads to the phenomena of work hardening and dynamic softening, represented on the curve as a stress peak, with a decrease in the stress level during hot deformation [10] . Thus, the phenomena of hot deformation involve the parameters of work hardening (h) and DRV (r) in the first part of the curve; as well as the parameters of dynamic softening after the peak, the Avrami exponent (n) and the time required for 50% recrystallization (t0.5), which can be used to optimize the parameters in various deformation conditions [11] .
The characterization of the thermomechanical behavior of stainless steels based on constitutive equations provides an excellent database for modeling of industrial proce- sses such as rolling and forging. According to the literature, on the first part of the curve, before the peak, the main formalism applied is the Estrin-Mecking-Bergstrom model [12] [13] . This model is based on the growth in dislocation density (ρ) during deformation (ε) resulting from the competition between the storage and annihilation of dislocations on the first part of the curve, where work hardening and DRV predominate. Equation (3) depicts the competition between these two mechanisms:
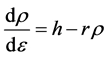 (3)
(3)
where the first term on the right side represents the contribution of work hardening or the work hardening rate (h) and the second term represents the contribution of DRV or the DRV rate (r), considering that hardening is constant relative to deformation and that DRV follows a first order reaction [14] . After algebraic manipulations, one reaches the equation that describes the stress (σ) vs. strain (ɛ) relationship for materials that soften intensely by DRV when isothermally deformed, Equation (4):
 (4)
(4)
After a period of increasing stress deformation, the stress tends towards a hypothetical value of saturation (σsat), which can be attributed to the equilibrium between dislocation storage and annihilation rates, with dρ/dε = 0. With additional algebraic manipulation (differentiation) [15] , one has:
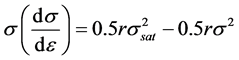 (5)
(5)
which is the equation of the tangent curve of the θσ vs. σ² graph with m = −0.5r. It should be noted that there are no studies that portray the profile of curves based on these coefficients of hardening (h) and DRV (r) up to the stress peak.
The characterization of the second part of the curve, after the peak, can be expressed following the Avrami formalism, where the equation describes DRX based on the evolution of the recrystallized fraction along the applied deformation, Equation (6) [16] [17] :
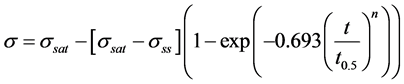 (6)
(6)
where n is the Avrami exponent associated with nucleation sites, t0.5 represents the time required for 50% of recrystallized fraction, σsat is the saturation stress when only DRV occurs, and σss is the steady state stress, with all the parameters expressed as power laws with the Zener-Hollomon parameter (Z) [18] .
The objective of this research is to characterize the thermomechanical behavior of a 16.6Cr-12Ni-2.1Mo-1.4Mn-0.08N-0.025C austenitic stainless steel based on the parameters of work hardening (h), dynamic recovery (r) and dynamic recrystallization (n, t0.5), considering constitutive equations (σ, ɛ) with deformation conditions expressed according to the Zener-Hollomon parameter (Z) and also the width (w) and depth (d) of the dip generated in the curve of the work hardening rate (θ) vs. equivalent stress (σ).
3. Materials and Methods
The material was obtained in the form of 3/4" diameter rolled bars, solubilized at 1030˚C for 60 min and water cooled, with an average initial grain size of 47 μm.
In the continuous isothermal hot torsion tests, cylindrical specimens (L = 11 mm; φ = 8.0 mm) were heated to a soak temperature of 1200˚C in an infrared radiation furnace coupled to a G-III hot torsion testing machine, left there for 300 s to homogenize the microconstituents, and then cooled at a rate of 3.3˚C/s to the deformation temperature, which were done at 1000˚C, 1050˚C, 1100˚C and 1150˚C. The specimens remained at these temperatures for 30 seconds to eliminate temperature gradients, and then deformed at strain rates of 0.1, 0.5, 1.0 and 5.0 s−1 to a deformation of 3.5. Immediately after deformation, the test specimens were quenched in water for metallurgical analysis.
The equivalent stress and strain values (σeq, ɛeq) were calculated by means of the Von Mises distributions, based on the method of Fields and Backofen [19] , where the curves are dependent on torque (M) and rotation angle (θ), according to Equations (7) and (8).
 (7)
(7)
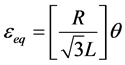 (8)
(8)
where R is the radius and L is the length of the useful part of the specimen. The coefficients n and m are related to the sensitivity to hardening and deformation rates.
For application of the method and characterization, the curves were initially analyzed using the Origin 9.0 mathematical manipulation program to eliminate irregularities, noise and fluctuations on the experimental curves. The values of peak stress (σp) and steady state stress (σss) were determined directly from the experimental curves. The values of critical stress (σc) and saturation stress (σsat) were determined by means of analytical methods, establishing the curves of work hardening rate (θ) as a function of applied stress (σ) up to the peak stress, with a 3rd order polynomial fit, followed by second order differentiation to determine the minimum value of the derivative that represents the inflection point on the curve and the onset of DRX (σc).
To characterize the first part, the curves of the product of the hardening rate were built based on the stress (θσ) vs. square of the stress (σ2) to determine the curvature (m = −0.5r), where r is the coefficient of DRV. The values of the strain hardening parameter (h) were determined according to the relation [15] :
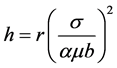 (9)
(9)
The second part of the curve, after the peak stress, was characterized according to the values of the Avrami exponent (n) and the time required to attain to 50% of DRX (t0.5), based on the fraction of dynamic softening (Xs) along the applied deformation. These parameters were determined from the rearrangement of Equation (6), 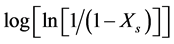 vs. logt, where the exponent n is the slope of the curve that allows the progress of dynamic softening to be evaluated. Another way to evaluate the DRX kinetics is from the curve of the work hardening rate (θ) vs. equivalent stress (σ), where the curves were shifted and overlapped at the highest level of stress attained, in order to assess the width (w) and depth (d) of the dip in dynamic softening with the deformation parameters.
vs. logt, where the exponent n is the slope of the curve that allows the progress of dynamic softening to be evaluated. Another way to evaluate the DRX kinetics is from the curve of the work hardening rate (θ) vs. equivalent stress (σ), where the curves were shifted and overlapped at the highest level of stress attained, in order to assess the width (w) and depth (d) of the dip in dynamic softening with the deformation parameters.
The torsion samples were sectioned 250 µm from the outer surface parallel to the axis of the rolling direction in the center in order to avoid the oxidized area for microstructural examination carried out by optical microscopy (OM), with electrochemical etching using 65% nitric acid (HNO3), at a current density of 1A/cm² and variable time. The average grain size was measured according to the ASTM E112 standard [20] , using ten images per sample. The details of the competing DRV-DRX phenomena were examined in a scanning electron microscope (SEM), in which the EDS analyses were performed to identify the phases present, while the thermochemical calculations were made via FactSage FSSteel database 5.6 [21] .
4. Results and Discussion
4.1. Stress-Strain Curves
Figure 1 illustrates the curves obtained in the hot torsion tests of the steel at different temperatures and strain rates. Note that, initially, there is a region of increased stress level in response to the applied deformation, followed by a change in the curvature for further deformation, reaching a maximum at the peak stress (σp). This behavior is characteristic of materials that undergo work hardening and dynamic recovery. After the peak, there is a region of dynamic softening where the stress decreases to an intermediate level between the stress at the onset of plastic flow (σo) and the peak stress (σp). This behavior is typical of materials that recrystallize dynamically, competing with the mechanism of dynamic recovery, which may or not reach steady state stress (σss).
In the first part of the curves, note the visible decrease in the level of stress in response to increasing temperature and decreasing strain rate. Moreover, in low strain rate and high temperature conditions, the hardening rate decreases rapidly until the peak stress is reached; in these conditions, note that the curvature is also more pronounced. On the other hand, in high strain rate and low temperature conditions, there is a high level of work hardening up to the peak. Immediately after the peak, note the subtle thresholds, which are probably formed due to the effect of DRV with average SFE, the presence of second phase particles responsible for the marked kinetics of DRV, competing with DRX and work hardening. Later, after the peak, intense softening by DRV occurred, with a marked reduction in the level of stress (∆σ~40 MPa) to the steady state, with retardation of the process, particularly in the conditions of low temperature and high strain rate, which hindered the operation of the thermally activated mechanisms, establishing a dynamic imbalance between the DRV and DRX rates. Moreover, the higher the strain rate the greater the difference between peak stress and steady state stress, due to the strong action of the hardening mechanism, leaving the material with low ductility, as reported in the literature [22] .


Figure 1. Stress-strain curves obtained from the thermomechanical simulations: (a) 0.1 s−1; (b) 0.5 s−1; (c) 1.0 s−1; (d) 5.0 s−1.
4.2. Activation Energy and Constitutive Equations
As can be seen, the level of stress in any condition depends on the deformation conditions, i.e., temperature and strain rate. Taking peak stress as a representative point of the material’s behavior, it is clear that the peak stress (σp) increases in response to the imposed strain rate and decreases with temperature, as shown in Figure 2. The generalized Arrhenius-type hyperbolic sine equation for hot working proposed by Sellars and Tegart [23] represents well the relationship between strain and stress conditions required to deform the material:
 (10)
(10)
where  is the deformation rate,
is the deformation rate, 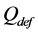 is the deformation activation energy (J/mol), R is the universal gas constant (8.31 J/mol∙K), T is the absolute temperature (K), Z is the Zener-Hollomon parameter, and σp is the peak stress (MPa). These are constants that depend on the variables A,
is the deformation activation energy (J/mol), R is the universal gas constant (8.31 J/mol∙K), T is the absolute temperature (K), Z is the Zener-Hollomon parameter, and σp is the peak stress (MPa). These are constants that depend on the variables A, 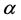 and n of the material. After some manipulations, a relationship was obtained which enabled us to determine the stress exponent (n) at a constant temperature and the activation energy (Qdef) at a constant strain rate [24] .
and n of the material. After some manipulations, a relationship was obtained which enabled us to determine the stress exponent (n) at a constant temperature and the activation energy (Qdef) at a constant strain rate [24] .
A computational method derived from the methodology proposed by Uvira and Jonas [25] was used to calculate the apparent activation energy (Qdef) for the hot deformation of the steel under study. Using this method, a value of α was determined that best

Figure 2. Dependence of peak stress on the (a) strain rate and (b) deformation temperature imposed in the tests.
fitted Equation (10). After substituting the σp values for all conditions of strain rate and temperature in Equation 10, linear regressions were used to determine the value of n for a variation in the values of α (0.002 <α < 0.052). The value of α used here is the value that generated the lowest standard deviation for the values of n at all the tested temperatures.
The value of α for the steel was found to be 0.011 MPa−1. The ln(ε) vs. ln[sinh(ασp)] graph in Figure 3 shows that the strain rate has the same effect on the peak stress at each temperature, since the lines are parallel, defining the average value of n as 4.25.
The value of n is associated with the active deformation mechanism, and the literature reports that thermally activated dynamic systems have values of n between 3 < n < 6 [16] . Based on the values of the α and n constants of the steel, the apparent activation energy for hot deformation (Qdef) of 347 kJ/mol was found in these deformation conditions, which is consistent with results reported in the literature for similar steels [26] [27] . The activation energy normalizes the effects of temperature and strain rate, and the high value is an indication of how quickly the stress increases along the hot working window. This high value is attributed to some mechanisms that raise the stress level, possibly related to the high content of alloying elements.
Using the log graph Z vs. log[sinh(ασp)], not shown here, taking sinh(ασp) = 1, and making a linear regression analysis, an A value equal to 5.51 × 1011 s−1 was found, with a good correlation coefficient of 0.95, showing a good fit of the experimental data. This constitutive equation can be used to predict the stress levels in other hot deformation conditions of this alloy in industrial settings or even in 3D computer simulations of thermomechanical processes, leading to a reduction in the costs of production, design and analysis.
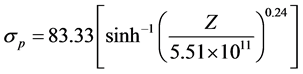 (11)
(11)
Figure 4 shows the relationships between the σc, σp stresses and the Z parameter, expressed as power laws. The values of the exponent n, which represents the sensitivity to
Figure 3. Variation of the hyperbolic sine function as a function of peak stress for all the strain rates at the different temperatures.
Figure 4. Relationship between critical (close dot) and peak stress (open dot) relative to the Zener-Hollomon parameter (Z).
strain rate, are very similar to the values within the range reported in the literature, 0.07 < n < 0.18 [28] .


The effect of the processing conditions on the stresses, considering the activation energy (Qdef) expressed by the Zener-Hollomon parameter (Z), reveals a marked increase in stress with Z, and at high values of Z (1015), the stresses tend to increase markedly in response to minor variations in Z. The value of the exponent of Z (n = 0.14) in response to peak stress reflects the sensitivity of the material to the deformation conditions, with elevation of the work hardening rate occurring more slowly, generating a delay in dynamic softening with strong DRV.
4.3. Modeling of the Stress-Strain Curves (1st Part, before the Peak)
Figure 5 presents the (θ×σ) vs. σ2 curve, where the m slope is equal to −0.5r. The value of the parameter of DRV (r), which specifies the inflection on the first part of the curve,
Figure 5. Determination of the DRV parameter (r) in the condition of 1050˚C/1.0 s−1.
presented variations between 6.2 < r < 9.4, with values within the range reported in the literature for stainless steels, 6 < r < 10 [11] [14] [29] [30] . Note that the parameter r decreased with increasing strain rate, decreasing deformation temperature, and increasing peak stress (σp), where the DRV is less effective with less influential diffusion mechanisms, increasing the σc/σp ratio and requiring higher strains to trigger DRX. This behavior is physically reasonable, since the DRV rate accelerates as the temperature increases and the strain rate decreases.
The determination of the work hardening parameter, h, depicted in Figure 6(a), showed variations at two orders of magnitude of h, increasing with the strain rate and decreasing temperature. Note that the behavior of parameter h shows higher values at low temperatures and high strain rates, with low mobility of dislocations, causing greater work hardening. On the other hand, h depends directly on stress and can be interpreted as the result of the mean free path of dislocations at the beginning of the curve and as the temperature increases with decreasing strain rate, causing a decrease in work hardening rate and thus reducing the value of h [11] [14] .
Figure 6(b) illustrates the dependence of the parameter r (DRV) as a function of the Zener-Hollomon parameter (Z), expressed as a power law according to equation 16. Note that r decreases as the parameter Z increases, and that the exponent is consistent with that reported in the literature for stainless steels, such as Wahabi (AISI 304H = −0.096 and AISI 304L = −0.066) and Moreira (AISI 304 = −0.084) [14] [29] .

It was also found that the parameter r, which specifies the curvature of the DRV curve, showed higher values in the tests performed at low strain rates and high temperatures, indicating that DRV occurs more rapidly at low values of Z. On the other hand, higher values of r caused the material to reach saturation stress (σsat) more rapidly with strong DRV, as shown in Figure 6(b). This behavior is due to the activation of thermally activated mechanisms with a moderate SFE of ~66.86 mJ/m2 [31] [32] . This value favors thermally activated mechanisms, modifying the deformed structure and the evolution of dislocation density, rendering DRV more effective, and delaying the onset of DRX. Moreover, other factors such as temperature, strain, and the concentration of

Figure 6. Dependence of the parameters of work hardening (h) and dynamic recovery (r) on (a) peak stress and (b) Zener-Hollomon, considering the hot deformation conditions.
alloying elements, which strongly influence the stability of the austenitic phase, also contribute to this effect.
The dependence of the strain hardening parameter (h), in power law, on the Z parameter shown in Equation (15), presented an upward trend:

The work hardening coefficient, h, contributed to increase the level of peak stress during deformation on the first part of the curve, modifying its profile, particularly at low temperatures and high strain rates. In this stage, immovable dislocations are formed and increase in density, accumulating and interacting randomly, becoming entrapped and forming less mobile subgrains, thus requiring a higher level of stress to cause greater plastic deformation [33] . However, the operation of thermally activated mechanisms, such as escalation and cross-slip, promote the rearrangement and annihilation of dislocations, favoring the formation of substructures, reducing the work hardening rate and increasing the coefficient of DRV (r). Note that the parameter r varies inversely to the parameter h in terms of dependence on Z, which is due to the competing action of the two mechanisms in the first part of the curve.
4.4. Modeling of the Stress-Strain Curves (2nd Part, after the Peak)
Figure 7 depicts the dependence of the dynamic softening fraction (Xs) as a function of deformation time, expressed by the sigmoidal curve, using the Avrami formalism. Note that the softening rate accelerates as the temperature and strain rate increase. At a given temperature, the t0.5 decreases with increasing strain rate; e.g., in the condition of 1000˚C/0.1 s−1, with t0.5 of 7.3 s dropping to 0.38 s at the same temperature when the strain rate increases to 5.0 s−1. At a given strain rate, t0.5 also decreases with increasing temperature. It should be noted that dynamically recrystallized fraction (XDRX) differs from the dynamic softening fraction (Xs) resulting from the action of DRV, which can be expressed according to the ratio σsat/σss = 1.75. On the other hand, the high value of Xs corresponds to an accelerated behavior in the region of DRX after the peak, with intragrain softening and high driving force, as well as a greater concentration of defects.
Figure 7. Dynamic softening fraction (Xs) curves as a function of deformation time, at varying temperatures and strain rates.
Thus, the greater the variation in the level of Δσ = σsat − σss stress the greater the driving force for DRX.
To estimate the Avrami exponent (n), Equation (6) was rearranged by plotting the 
In this set of isothermal hot torsion tests, the ratio that best represented the time dependence to attain 50% of softening (t0.5), with the deformation conditions set forth in Equation (16), (see Figure 9 and Figure 10) was found to be:

The dependence of the Avrami exponent (n) on the parameter Z, according to the deformation conditions that best fit the experimental data according to Equation (17) and expressed in Figure 10, was found to be:

The relationship between t0.5 and the depth (d) and width (w) of the dip of the curve generated in the softening region (negative strain hardening rate) is linear, i.e., the longer the t0.5 the greater the depth (d) and width (w) of the dip. On the other hand, the r value decreased, accelerating the softening kinetics. The simplicity of this method stems from the small number of experiments it requires, even when numerous parameters are involved. It is worth noting that the kinetics of dynamic softening determined with this methodology encompasses all the active softening mechanisms. In other words, not only the effects of DRV but also those of DRX are computed in the calculated values of t0.5, showing a correlation coefficient of 0.99, as indicated in Figure 10.


Figure 8. Determination of the Avrami exponent (n) based on the 
Figure 9. Determination of the time to attain 50% of softening (t0.5) as a function of parameter Z.
4.5. Comparison between the Modeling and Experimental Curves
The experimental and simulated curves are presented in Figure 11. Note that there is good agreement, despite some mismatches, particularly in the first part of the curves, where, in the conditions of 1000˚C to 1050˚C and strain rates of 0.1 and 0.5 s−1. The simulated curves present a higher share in the DRV rate (high r). The relative shift of

Figure 10. Correlation between calculated and experimental values of (a) t0.5 and (b) n, with a correlation coefficient of 0.99, according to the deformation conditions.


Figure 11. Comparison between experimental and simulated plastic flow curves: (a) 5.0 s−1; (b) 1.0 s−1; (c) 0.5 s−1; (d) 0.1 s−1.
the curves to the left with respect to peak deformation, in response to higher work hardening, tends to generate differences in the real and simulated curves.
As for the kinetics of DRX in the second part of the curves, note that the delay in the process resulted in lower values of the Avrami exponent (n) and the time to attain 50% of dynamic softening (t0.5). The shape of the experimental and simulated curves showed differences in the conditions of 1000˚C and 1050˚C at strain rates of 0.1 and 0.5 s−1. Nevertheless, in modeling the curves, it is clear that the parameters n and t0.5 determine the shape of the curves by means of the kinetics of DRX, where higher values of n and lower values for t0.5 are associated with the kinetics of accelerated dynamic softening with low Z, as indicated in Figures 11(a)-(d).
4.6. Microstructural Analysis
Figure 12 illustrates the mechanical and microstructural evolution of the steel visualized by optical microscopy in the condition of 1000˚C/5.0 s−1 at strains of 0.4, 1.5 and 3.5. Note that the deformations close to the peak (ɛ = 0.4) show the presence of hardened grains and deformation twinning, and the onset of the formation of small recrystallized grains. With further deformation, after the peak stress (ɛ = 1.5), the presence of elongated grains in the direction of deformation is still visible, with some smaller grains at the boundaries of deformed grains, a sharp drop in the level of stress, and the presence of localized flow at the grain boundaries, indicating plastic instability [34] . As can be seen, the microstructural evolution of the grains affects the level of stress and therefore the shape of the curves, reaching a finer austenitic microstructure at a strain of deformation σss = 3.5, as indicated by the X-ray analyses in Figure 13. In addition, the transition from the level of peak (σp) to steady state (σss) stress caused a


Figure 12. Microstructure of the steel under hot torsion in the condition of 1000˚C/5.0 s−1 at strains of (a) 0.4; (b) 1.5; (c) 3.5; and (d) flow curve.
Figure 13. X-ray analysis of the material in the solubilized condition.
reduction in strength, increasing ductility with the refinement of austenitic grains in the hot working of the steel.
The microstructural features are presented in Figure 14 reveal the formation of new dynamically recrystallized chain-shaped grains at triple points, deformation twinning boundaries, deformed grain boundaries, and the presence of deformation bands, indicating heterogeneous nucleation with an Avrami exponent of n − 1. These grains, which migrate from their deformation induced boundaries, are responsible for dynamic softening, reducing the hardening rate with strain after the peak stress, until they reach the steady state, where dynamic equilibrium is established between hardening and softening with grain refinement, which is favored at low strain rates and high temperatures.
It is also worth noting the microstructural evidence of plastic instability with a deformation gradient at the grain boundaries, the presence of deformation bands, and concentration of dynamically recrystallized chain-shaped grains in the conditions of low temperature and high strain rate, which generate heterogeneous deformation with localized flow. On the other hand, in the conditions of high temperature and low strain rate, the kinetics of DRX is accelerated and homogeneous (n − 3), with new grain growth and a significant increase in the recrystallized fraction in response to increasing strain until the steady state is reached.
Figure 15 shows the SEM analysis of the samples in the conditions of 1000˚C, at a rate of 5.0 s−1 and strain of 1.5. Note the formation of small chain-shaped grains that migrate, induced by deformation, which are formed at deformed grain boundaries and twin boundaries, with evidence of localized flow, indicating instability of the material at some points. Also visible is the presence of precipitates at the grain boundaries, possibly chromium nitride, which can be confirmed by the phase diagram calculated using FSstel database in the FactSage software, as shown in Figure 16. However, in the conditions of 1150˚C at a rate of 1.0 s−1 and a strain of 3.5, the grains are fully recrystallized with grain refinement.


Figure 14. Microstructure under hot torsion in the condition of 1150˚C/0.1 s−1 at strain rates of 0.4, 1.5 and 3.5.

Figure 15. SEM microstructure analysis in the conditions of: (a) 1000˚C, at a rate of 5.0 s−1 and ε = 1.5; (b) 1150˚C, at a rate of 0.1 s−1 and ε = 3.5.
Figure 16. Thermodynamic calculation of the equilibrium diagram by Facts age of the as received samples as a function of temperature.
5. Conclusions
In this study, the dynamic softening of austenitic stainless steel was investigated at de- formation temperatures varying from 1000˚C to 1150˚C and strain rates of 0.1 s−1 to 5.0 s−1. The following conclusions can be drawn from this investigation.
1) The results indicated that plastic flow curves were significantly influenced by the conditions imposed during thermomechanical processing, and that the stress levels increased in response to the parameter Z at a high work hardening rate.
2) In the first part of the curves, the σc/σp ratio was relatively high, indicating that the softening promoted by DRV was intense, and a finding was corroborated by the highest values of r and the average stacking fault energy, γsfe = 66.86 mJ/m2, which facilitated the thermally activated mechanisms, increasing the effectiveness of DRV and delaying the onset of DRX.
3) The second part of the curves showed that there is a delay in the kinetics of dynamic softening with a higher value of t0.5 and lower values of the Avrami exponent (n), owing to the competing DRV and DRX mechanisms, and steady state stress (σss) reached at higher strain rates.
4) The microstructure presented work hardened grains with deformation twinning and the formation of small recrystallized grains on the first part of the curve. As deformation continued, after the peak, the presence of elongated grains was visible in the direction of deformation, with the formation of small dynamically recrystallized grains in the shape of chains at triple points, twin boundaries, deformed grain boundaries, the presence of chromium nitride precipitates, and formation of localized flow, indicating plastic instability of the material.
Acknowledgements
The authors acknowledge the financial support of the Brazilian research funding agencies FAPEMA (Maranhão Foundation for Scientific Research and Development) CNPq and CAPES. We are also grateful for the technical support provided by Prof. Dr. Regina Sousa (UFMA―Federal University of Maranhão) and MSc. José Renato Sucupira.
Cite this paper
Ferreira, R.P., Silva, E.S., Nascimento, C.C.F., Rodrigues, S.F., Aranas Jr., C., Leal, V.S. and Reis, G.S. (2016) Thermomechanical Behavior Modeling of a Cr-Ni-Mo-Mn-N Austenitic Stainless Steel. Materials Sciences and Applications, 7, 803-822. http://dx.doi.org/10.4236/msa.2016.712062
References
- 1. Baddoo, N.R. (2008) A Review of Research, Applications, Challenges and Opportunities. Journal of Constructional Steel Research, 64, 1199-1206.
https://doi.org/10.1016/j.jcsr.2008.07.011 - 2. Lo, K.H., Shek, C.H. and Lai, J.K.L. (2009) Recent Developments in Stainless Steels. Materials Science and Engineering R, 65, 39-104.
https://doi.org/10.1016/j.mser.2009.03.001 - 3. Byun, T.S., Hashimoto, N. and Farrell, K. (2004) Temperature Dependence of Strain Hardening and Plastic Instability Behaviors in Austenitic Stainless Steels. Acta Materialia. 52, 3889-3899.
https://doi.org/10.1016/j.actamat.2004.05.003 - 4. Sousa, R.C., Silva, E.S., Jorge, Jr., A.M., Cabrera, J.M. and Balancin O. (2013) Dynamic Recovery and Dynamic Recrystallization Competition on a Nb- and N-Bearing Austenitic Stainless Steel Biomaterial: Influence of Strain Rate and Temperature. Materials Science and Engineering A, 582, 96-107.
https://doi.org/10.1016/j.msea.2013.06.037 - 5. Ebrahimi, G.R., Keshmiri, H., Maldar, A.R. and Momeni, A. (2012) Dynamic Recrystallization Behavior of 13%Cr Martensitic Stainless Steel under Hot Working Condition. Journal of Materials Science and Technology, 28, 467-473.
https://doi.org/10.1016/S1005-0302(12)60084-X - 6. Nkhoma, R.K.C., Siyasiya, C.W. and Stumpf, W.E. (2014) Hot Workability of AISI 321 and AISI 304 Austenitic Stainless Steels. Journal of Alloys and Compounds, 595, 103-112.
https://doi.org/10.1016/j.jallcom.2014.01.157 - 7. Stewart, G.R., Jonas, J.J. and Montheillet, F. (2004) Kinetics and Critical Conditions for the Initiation of Dynamic Recrystallization in 304 Stainless Steel. ISIJ International, 44, 1581-1589.
https://doi.org/10.2355/isijinternational.44.1581 - 8. Poliak, E.I. and Jonas, J.J. (2003) Initiation of Dynamic Recrystallization in Constant Strain Rate Hot Deformation. ISIJ International, 43, 692-700.
https://doi.org/10.2355/isijinternational.43.692 - 9. Poliak, E.I. and Jonas, J.J. (1996) One-Parameter Approach to Determining the Critical Conditions for the Initiation of Dynamic Recrystallization. Acta Materialia, 44, 127-136.
https://doi.org/10.1016/1359-6454(95)00146-7 - 10. Ryan, N.D. and McQueen, H.J. (1989) Dynamic Recovery, Strain Hardening and Flow Stress in Hot Working of 316 Steel. Czechoslovak Journal of Physics B, 39, 458-465.
https://doi.org/10.1007/BF01597803 - 11. Sarkar, A., Marchattiwar, A., Chakravartty, J.K. and Kashyap, B.P. (2013) Kinetics of Dynamic Recrystallization in Ti-Modified 15Cr-15Ni-2Mo Austenitic Stainless Steel. Journal of Nuclear Materials, 432, 9-15.
https://doi.org/10.1016/j.jnucmat.2012.07.020 - 12. Mecking, H. and Kocks, U.F. (1981) Kinects of Flow and Strain-Hardening. Acta Metallurgica, 29, 1865-1875.
https://doi.org/10.1016/0001-6160(81)90112-7 - 13. Estrin, Y. and Mecking, H. (1984) A Unified Phenomenological Description of Work Hardening and Creep Based on One-Parameter Models. Acta Metallurgica, 32, 57-70.
https://doi.org/10.1016/0001-6160(84)90202-5 - 14. Jorge, Jr., A.M. and Balancin, O. (2005) Prediction of Steel Flow Stresses under Hot Working Conditions. Materials Research, 8, 309-315.
- 15. Jonas, J.J., Quelennec, X., Jiang, L. and Martin, E. (2009) The Avrami Kinetics of Dynamic Recrystallization. Acta Materialia, 57, 2748-2756.
https://doi.org/10.1016/j.actamat.2009.02.033 - 16. Rodrigues, S.F., Silva, E.S., Reis, G.S., Sousa, R.C. and Balancin, O. (2014) Prediction of Hot Flow Plastic Curves of ISO 5832-9 Steel Used as Orthopedic Implants. Materials Research, 17, 436-444.
https://doi.org/10.1590/S1516-14392014005000001 - 17. Xu, T.C., Peng, X.D., Qin, J., Chen, Y.F., Yang, Y. and Wei, G.B. (2015) Dynamic Recrystallization Behavior of Mg-Li-Al-Nd Duplex Alloy during Hot Compression. Journal of Alloys and Compounds, 639, 79-88.
https://doi.org/10.1016/j.jallcom.2015.03.144 - 18. Han, Y., Wu, H., Zhang, W., Zou, D., Liu, G. and Qiao, G. (2015) Constitutive Equation and Dynamic Recrystallization Behavior of As-Cast 254SMO Super-Austenitic Stainless Steel. Materials and Design, 69, 230-240.
https://doi.org/10.1016/j.matdes.2014.12.049 - 19. Fields, D.S. and Backofen, W.A. (1957) Determination of Strain Hardening Characteristics by Torsion Testing. Proceeding of American Society for Testing and Materials, 57, 1259-1272.
- 20. American Society for Testing and Materials (ASTM) E112 (2013) Standard Test Methods for Determining Average Grain Size.
- 21. Bale, C.W., Belisle, E., Chartrand, P., Decterov, S.A., Eriksson, G., Hack, K., Jung, I.H., Kang, Y.Y., Melancon, J., Pelton, A.D., Robelin, C. and Peterson, S. (2009) FactSage Thermomechanical Software and Database—Recent Developments. Calphad, 33,295-311.
https://doi.org/10.1016/j.calphad.2008.09.009 - 22. McQueen, H.J., Yue, S., Ryan, N.D. and Fry, E. (1995) Hot Working Characteristics of Steels in Austenitic State. Journal of Materials Processing Technology, 53, 293-310.
https://doi.org/10.1016/0924-0136(95)01987-P - 23. Sellars, C.M. and Tegart, W.J.M. (1966) La relation entre la résistance et la structure dans la deformation à chaud. Mémoires Scientifiques de la Revue de Metallurgie, 63, 731-746.
- 24. Laasraoui, A. and Jonas, J.J. (1991) Prediction of Steel Flow Stresses at High Temperatures and Strain Rates. Metallurgical and Materials Transactions A, 22, 1545-1558.
https://doi.org/10.1007/BF02667368 - 25. Uvira, J.L. and Jonas, J.J. (1968) Hot Compression of Armco Iron and Silicon Steel. Transactions of the Metallurgical Society of AIME, 242, 1619-1626.
- 26. Angella, G., Wynne, B.P., Rainforth, W.M. and Beynon, J.H. (2008) Strength of AISI 316L in Torsion at High Temperature. Materials Science and Engineering A, 475, 257-267.
https://doi.org/10.1016/j.msea.2007.05.089 - 27. Cabrera, P. (2001) High Temperature Deformation of 316 L Stainless Steel. Materials Science and Technology, 17, 155-161.
https://doi.org/10.1179/026708301101509944 - 28. Mirzadeh, H., Cabrera, J.M., Prado, J.M. and Najafizadeh, A. (2011) Hot Deformation Behavior of a Medium Carbon Microalloyed Steel. Materials Science and Engineering A, 528, 3876-3882.
https://doi.org/10.1016/j.msea.2011.01.098 - 29. Wahabi, M.E., Cabrera, J.M. and Prado, J.M. (2003) Hot Working of Two AISI 304 Steels: A Comparative Study. Materials Science and Engineering A, 343, 116-125.
https://doi.org/10.1016/S0921-5093(02)00357-X - 30. Momeni, A., Abbasi, S.M. and Badri, H. (2012) Hot Deformation Behavior and Constitutive Modeling of VCN200 Low Alloy Steel. Applied Mathematical Modelling, 36, 5624-5632.
https://doi.org/10.1016/j.apm.2012.01.008 - 31. Wendler, M., Hauser, M., Fabrichnaya, O., Krüger, L., Weiβ, A. and Mola, J. (2015) Thermal and Deformation-Induced Phase Transformation Behavior of Fe-15Cr-3Mn-3Ni-0.1N-(0.05-0.25)C Austenitic and Austenitic-Martensitic Cast Stainless Steels. Materials Science and Engineering A, 645, 28-39.
https://doi.org/10.1016/j.msea.2015.07.084 - 32. Song, R., Xiang, J. and Hou, D. (2011) Characteristics of Mechanical Properties and Microstructure for 316L Austenitic Stainless Steel. International Journal of Iron and Steel Research, 60, 117-119.
- 33. Humphreys, F.J. and Hatherly, M. (2004) Recrystallization and Related Annealing Phenomena. 2nd Edition, Elsevier, Oxford, 187-194.
- 34. Mataya, M.C., Nilsson, E.R., Brown, E.L. and Krauss, G. (2003) Hot Working and Recrystallization of As-Cast 316L. Metallurgical Transactions A, 34, 1683-1703.
https://doi.org/10.1007/s11661-003-0313-8








