Materials Sciences and Applications
Vol.06 No.06(2015), Article ID:56797,6 pages
10.4236/msa.2015.66049
Structure Evolution in Austenitic Stainless Steels
―A State Variable Model Assessment
Paul S. Follansbee
Boyer School of Natural Sciences, Mathematics, and Computing, Saint Vincent College, Latrobe, USA
Email: paul.follansbee@stvincent.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 April 2015; accepted 26 May 2015; published 29 May 2015
ABSTRACT
Strain hardening in austenitic stainless steels is modeled according to an internal state variable constitutive model. Derivation of model constants from published stress-strain curves over a range of test temperatures and strain rates is reviewed. Model constants for this material system published previously are revised to make them more consistent with model constants in other material systems.
Keywords:
Constitutive Modeling, Internal State Variable, Austenitic Stainless Steel, Strain Hardening

1. Introduction
The constitutive behavior of annealed, austenitic stainless steels was recently analyzed according to an internal state variable model [1] [2] . In this model, which has been described in detail by Follansbee [2] , the temperature and strain-rate dependent yield stress, σ, of annealed material (with a low initial dislocation density) is modeled as
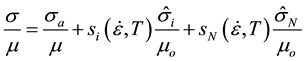 (1)
(1)
where σa is an athermal stress (e.g., due to the strengthening contribution of grain boundaries), 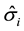 is an internal state variable characterizing the strengthening contribution of solute element additions, and
is an internal state variable characterizing the strengthening contribution of solute element additions, and 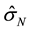 is an internal state variable characterizing the strengthening contribution due to nitrogen, μ is the temperature-dependent shear modulus, μo is the shear modulus at 0 K, and si and sN are functions (varying from zero to unity) that describe the temperature (T) and strain rate
is an internal state variable characterizing the strengthening contribution due to nitrogen, μ is the temperature-dependent shear modulus, μo is the shear modulus at 0 K, and si and sN are functions (varying from zero to unity) that describe the temperature (T) and strain rate 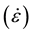 dependence of the two strength contributions. The explicit nitrogen-de- pendent term in Equation (1) evolved from analysis of two extensive data sets documenting the effect of the nitrogen content on the temperature-dependent yield stress in austenitic stainless steels [3] [4] .
dependence of the two strength contributions. The explicit nitrogen-de- pendent term in Equation (1) evolved from analysis of two extensive data sets documenting the effect of the nitrogen content on the temperature-dependent yield stress in austenitic stainless steels [3] [4] .
The addition of strain-hardening is modeled by adding another internal state variable to Equation (1):
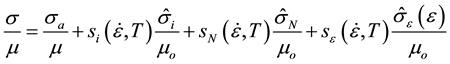 (2)
(2)
where 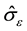 is the internal state variable characterizing interactions of mobile dislocations with stored (or immobile) dislocations and sε defines the temperature and strain-rate dependence of these interactions. The analysis of temperature and strain-rate dependent yield stress measurements in a variety of austenitic stainless steels led to the following definitions of si, sN, and sε, where k is Boltzmann’s constant and b is the Burgers vector:
is the internal state variable characterizing interactions of mobile dislocations with stored (or immobile) dislocations and sε defines the temperature and strain-rate dependence of these interactions. The analysis of temperature and strain-rate dependent yield stress measurements in a variety of austenitic stainless steels led to the following definitions of si, sN, and sε, where k is Boltzmann’s constant and b is the Burgers vector:
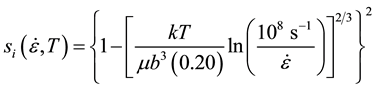 (3)
(3)
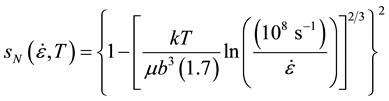 (4)
(4)
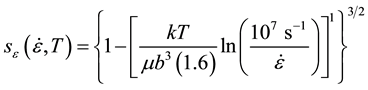 (5)
(5)
Consistent with an internal-state variable formulation, the strain-dependence of 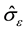 is defined by the differential
is defined by the differential
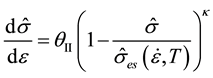 (6)
(6)
where θII is the stage two hardening rate (e.g., of a single crystal), κ is a constant, and 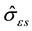 is the temperature and strain-rate dependence saturation threshold stress. When κ equals unity, Equation (3) becomes the Voce Law. According to Equation (6) the rate of strain hardening begins at θII and approaches zero as
is the temperature and strain-rate dependence saturation threshold stress. When κ equals unity, Equation (3) becomes the Voce Law. According to Equation (6) the rate of strain hardening begins at θII and approaches zero as 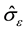 approaches
approaches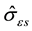 . Finally, the temperature and strain rate dependence of
. Finally, the temperature and strain rate dependence of 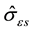 is described using a dynamic recovery model [5]
is described using a dynamic recovery model [5]
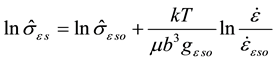 (7)
(7)
where 



2. Evaluating the Evolution Equation
The temperature and strain-rate dependence of evolution (strain hardening) is evaluated by analyzing stress- strain curves measured at various temperatures and strain rates. Rewriting Equation (2),

A key premise of the internal-state variable model applied here is that evolution does not alter the parameters on the right-hand side of Equation (8)―except of course for σ(ε). This premise was shown to be approximately valid by Follansbee and Kocks, through extensive measurements of the evolution of the internal state variable in pure copper [6] . In applying Equation (8) to stress-strain curves measured in an annealed austenitic stainless
steel, introduction of correct values of








3. Stress-Strain Measurements in AISI 304 and AISI 316 Stainless Steels
Table 1 lists the source of 18 measurements of stress-strain curves in AISI 304 and AISI 316 stainless steels (and variations of these alloys). The data set was selected because of the wide range of temperatures and strain rates investigated, which is necessary for evaluation of the constants in Equation (7). Included in Table 1 are the grain sizes and the nitrogen contents (when specified). The nitrogen contents are listed because of the correlation of the state variable 












The next step of the analysis is to fit Equation (6) to the 





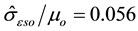





Figure 1. Analysis of the Albertini and Montagnani stress-strain curve at 295 K and a strain rate of 0.004 s−1 according to Equation (8) to give 
Table 1. Stress-strain measurements in annealed AISI 316 and AISI 304 stainless steels (and variations of these alloys) analyzed in this study.
aThe final temperatures for tests under adiabatic conditions are listed in parentheses; bThe material received a “stress relief anneal”; these treatments are well above the recrystallization temperature of 850˚C and would yield a grain size of 30 μm to 60 μm, depending on the heat treatment time [15] ; cThe material was reportedly heat treated at 1050˚C for 30 minutes; this is a common solution anneal condition, also well above the recrystallization temperature of 850˚C, that would yield a grain size of 40 μm to 60 μm [15] .
Figure 2. Fit of Equation (6) to the deduced values of 




Each of the measurements listed in Table 1 was analyzed with κ = 2 as described above. Model parameters (



The parameters in the last column of Table 1 suggest a slight strain-rate dependence of θII. While the extensive measurements by Follansbee and Kocks in copper [6] indicated this strain-rate dependence, one would not conclude this with the limited data set in the stainless steels presented here. The indicated strain-rate dependence is assumed based on the earlier measurements, and the assumed correlation is

where the strain rate 
The dependence of 



The four open squares in Figure 4 that fall well off the line are for the Albertini and Montagnani data set at 823 K [7] , the Steichen data set at 811 K and a strain rate of 3 × 10−5 s−1 [8] , the Conway et al data set at 703 K [10] , and the Dai et al data set at 623 K [12] . It was proposed in [2] that dynamic strain aging becomes active at these high temperatures, which leads to behavior that deviates strongly from that described by Equation (7). A method to include the higher stresses during dynamic strain aging into the constitutive model was introduced in [2] .
Figure 3. Fit of Equation (6) to the Stout and Follansbee stress-strain curve in 304L SS at 295 K and a strain rate of 100 s−1 and the Antoun stress-strain curve in 304 SS at 344 K and a strain rate of 0.001 s−1.
Figure 4. Saturation threshold stress 
4. Summary
Analysis of stress-strain curves reported for annealed austenitic stainless steels has given further evidence of the application of the internal state variable constitutive formulism developed by the author and coworkers. Of particular interest here was the derivation of model parameters describing strain-hardening. A set of model parameters for this alloy system was given in previous publications [1] [2] , but the derivation of these parameters was not presented in these earlier publications.
The reanalysis of the literature stress-strain curves presented here demonstrated that the model parameters in Equations (6) and (7) are somewhat co-dependent. In particular, a high value of κ along with a high value of 


Acknowledgements
The author appreciates the support of Saint Vincent College in the writing of [2] and the compilation of this manuscript.
References
- Follansbee, P.S. (2012) An Internal State Variable Constitutive Model for Deformation of Austenitic Stainless Steels. Journal of Engineering Materials and Technology, 134, 41007-1-41007-10. http://dx.doi.org/10.1115/1.4006822
- Follansbee, P.S. (2014) Fundamentals of Strength―Principles, Experiment, and Application of an Internal State Variable, Constitutive Formulation. The Minerals, Metals, & Materials Society, John Wiley & Sons, Hoboken.
- Norström, L.-Å. (1977) The Influence of Nitrogen and Grain Size on Yield Strength in Type AISI 316L Austenitic, Stainless Steel. Metal Science, 11, 208-212. http://dx.doi.org/10.1179/msc.1977.11.6.208
- Brynes, M.L.G., Grujicic, M. and Owen, W.S. (1987) Nitrogen Strengthening of a Stable Austenitic Stainless Steel. Acta Metallurgia, 37, 1853-1862. http://dx.doi.org/10.1016/0001-6160(87)90131-3
- Kocks, U.F. (1976) Laws for Work-Hardening and Low-Temperature Creep. ASME Journal of Engineering Materials and Technology, 98, 76-85. http://dx.doi.org/10.1115/1.3443340
- Follansbee, P.S. and Kocks, U.F. (1988) A Constitutive Description of the Deformation of Copper Based on the Use of the Mechanical Threshold Stress as an Internal State Variable. Acta Metallurgica, 36, 81-93. http://dx.doi.org/10.1016/0001-6160(88)90030-2
- Albertini, C. and Montagnani, M. (1980) Dynamic Uniaxial and Biaxial Stress-Strain Relationships for Austenitic Stainless Steels. Nuclear Engineering and Design, 57, 107-123. http://dx.doi.org/10.1016/0029-5493(80)90226-5
- Steichen, J.M. (1971) High Strain Rate Mechanical Properties of Types 304 Stainless Steel and Nickel 200 (RM-14). Hanford Engineering Development Laboratory, HEDL-TME-71-145, Richland, WA.
- Semiatin, S.L. and Holbrook, J.H. (1982) Isothermal Plastic Flow Behavior of Annealed 304L Stainless Steel. Final Technical Report to Sandia National Laboratories, Contract Number SN4156-PO92-9342, Battelle Columbus Laboratories.
- Conway, J.B., Stentz, R.H. and Berling, J.T. (1974) Fatigue, Tensile, and Relaxation Behavior of Stainless Steels. Report commissioned by the US Atomic Energy Commission, Division of Reactor Research and Development, NTIS, TID26135.
- Byun, T.S., Hashimoto, N. and Farrell, K. (2004) Temperature Dependence of Strain Hardening and Plastic Instability Behaviors in Austenitic Stainless Steels. Acta Materialia, 52, 3889-3899. http://dx.doi.org/10.1016/j.actamat.2004.05.003
- Dai, Y., Egeland, G.W. and Long, B. (2008) Tensile Properties of ECX316LN Irradiated in SINQ to 20 dpa. Journal of Nuclear Materials, 377, 109-114. http://dx.doi.org/10.1016/j.jnucmat.2008.02.035
- Stout, M.G. and Follansbee, P.S. (1986) Strain Rate Sensitivity, Strain Hardening, and Yield Behavior of 304L Stainless Steel. Journal of Engineering Materials and Technology, 108, 344-353. http://dx.doi.org/10.1115/1.3225893
- Antoun, B.R. (2004) Temperature Effects on the Mechanical Properties of Annealed and HERF 304L Stainless Steel. Sandia National Laboratories, Sandia Report, SAND2004-3090.
- Schino, A.D., Abbruzzese, G. and Kenny, J.M. (2003) Recrystallization and Grain Growth in Austenitic Stainless Steels: A Statistical Approach. Journal of Materials Science &Technology, 19, 119-121.
NOTES
1Only a κ = 2 is selected; the remaining parameters arise from the fit to the full data set listed in Table 1 as described below. Agreement with the data, although, is not as good with κ = 1.
2For the three adiabatic tests, the final rather than the initial temperature is plotted in Figure 4.








