Materials Sciences and Applications
Vol. 3 No. 11 (2012) , Article ID: 24720 , 11 pages DOI:10.4236/msa.2012.311109
Ductile Fracture Characterization for Medium Carbon Steel Using Continuum Damage Mechanics
![]()
Department of Metallurgical and Materials Engineering, Escola Politécnica, University of São Paulo, São Paulo, Brazil.
Email: *tsiloufas@usp.br, rlplaut@usp.br
Received August 2nd, 2012; revised September 3rd, 2012; accepted October 2nd, 2012
Keywords: Continuum Damage Mechanics; Tensile Testing; Numerical Simulation; Medium Carbon Steels
ABSTRACT
This paper presents the ductility characterization for a medium carbon steel, for two microstructural conditions, that has been evaluated using the continuum damage mechanics theory, as proposed by Kachanov and developed by Lemaitre. Tensile tests were carried out using loading-unloading cycles in order to capture the gradual deterioration of the elastic modulus, which may be linked to the ductile damage increase with increasing plastic strain. The mechanical parameters for the isotropic damage evolution equation were obtained and then used as inputs for a plasticity-damage coupled numerical algorithm, validated through numerical simulations of the experimental tensile tests. A comparison between the SAE 1050 steels studied and two carbon steel alloys (obtained from the literature), provided some basic understanding of the influence of the carbon level on the evolution of the damage parameters. An empiric relationship for this set of parameters, which can provide useful data for preliminary studies envisaging prediction of ductile failure in carbon steels, is also presented.
1. Introduction
Ductile fracture is the failure of a solid material due to nucleation, coalescence and growth of cavities induced by plastic deformation. There are several ways, from empiric relationships [1,2] to porous media stiffness modeling [3], developed to study this phenomenon in order to predict when a workpiece will fail under a given stressstrain state.
Kachanov, in 1958 [4], first proposed a continuum damage variable to represent the surface density of cavities in a given infinitesimal volume element. By the 70’s, researchers embraced the idea and developed a theory based on the framework of irreversible processes thermodynamics to model the evolution of this damage variable and how it affects mechanical properties, such as elastic modulus and stresses, leading to the eventual failure of a material [5]. This theory, called Continuum Damage Mechanics (CDM), is complementary to Fracture Mechanics, since it is concerned about the nucleation and growth of cavities until they reach a critical size turning into a macroscopic crack, whose propagation in a solid media is studied by the latter.
For damage evolution caused by large plastic deformation, Lemaitre and Chaboche developed the first and simplest model [6-10], which considers a linear evolution of isotropic damage with plastic strain in a uniaxial stress state condition. This model was later expanded by other authors, adding new capabilities such as dealing with anisotropic damage [11], or with non-linear damage evolution [12-16].
Recently, medium carbon steel heat-treated to obtain spheroidized cementite in its microstructure is being used as raw material for sheet forming processes, due to its better formability properties [17]. Due to large plastic strains imposed to this kind of manufactured parts, cracks and other defects observed are mostly related to ductile damage evolution.
With this motivation, in this work the ductile fracture of SAE 1050 steel was studied, for two different microstructural conditions namely: lamellar ferrite-pearlite and spheroidized cementite, under the continuum damage mechanics point of view. Experimental characterization of isotropic damage evolution was carried out and numerical simulations were performed in order to predict failure.
2. Continuum Damage Mechanics Model for Ductile Fracture
The continuum damage variable introduced by Kachanov is defined as the relationship between the sectional area of voids 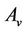 and the overall sectional area
and the overall sectional area 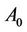 of a given surface in a volume element. Assuming the hypothesis of isotropic deterioration of the material, the damage can be written as:
of a given surface in a volume element. Assuming the hypothesis of isotropic deterioration of the material, the damage can be written as:
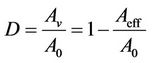 (1)
(1)
where 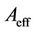 is the effective resisting area. It may be observed that this definition is the same one as the microvoid area fraction used is some micromechanical theories, such as McClintock’s [18]. The damage variable can assume any value between 0 and 1, covering from a virgin state to a completely damaged one, although real materials will fail when the damage reaches a critical value
is the effective resisting area. It may be observed that this definition is the same one as the microvoid area fraction used is some micromechanical theories, such as McClintock’s [18]. The damage variable can assume any value between 0 and 1, covering from a virgin state to a completely damaged one, although real materials will fail when the damage reaches a critical value , when the effective area can no longer resist the applied load, leading to the formation of a macroscopic crack.
, when the effective area can no longer resist the applied load, leading to the formation of a macroscopic crack.
In his model, Lemaitre assumes the hypothesis of strain equivalence, which states that the damaged material will have the same constitutive behavior of the virgin material, replacing the stress tensor  by the effective stress tensor
by the effective stress tensor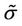 , defined as:
, defined as:
 (2)
(2)
One important consequence of this assumption is that one can define an effective elastic modulus of a damaged material, giving an indirect way to measure the damage in a solid, by monitoring the evolution of the Young modulus with increasing strain:
 (3)
(3)
where 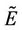 is the effective elastic modulus and
is the effective elastic modulus and  is the elastic modulus for the undamaged material.
is the elastic modulus for the undamaged material.
Using as basis the thermodynamic of irreversible processes [19], CDM treats the damage as an internal thermodynamic state variable, and so its evolution can be derived assuming the existence of a potential of dissipation 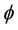 and an associated variable Y, named damage strain energy release rate and defined as [10]:
and an associated variable Y, named damage strain energy release rate and defined as [10]:
 (4)
(4)
where  is the von Mises equivalent stress,
is the von Mises equivalent stress,  is the deviatoric stress tensor,
is the deviatoric stress tensor,  is the Poisson’s ratio and
is the Poisson’s ratio and  is the hydrostatic stress. Further, Lemaitre [10] shows that the damage evolution can be written as:
is the hydrostatic stress. Further, Lemaitre [10] shows that the damage evolution can be written as:
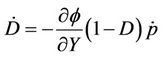 (5)
(5)
with  defined as the accumulated plastic strain and
defined as the accumulated plastic strain and 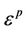 being the plastic strain tensor. The choice of a proper potential of dissipation that can represent experimental results is the core of any CDM model. In Lemaitre and Chaboche’s model, the hypothesis of isotropic damage, existence of a strain threshold for damage initiation and linear evolution of the damage with the accumulated plastic strain leads to the following equation for damage evolution:
being the plastic strain tensor. The choice of a proper potential of dissipation that can represent experimental results is the core of any CDM model. In Lemaitre and Chaboche’s model, the hypothesis of isotropic damage, existence of a strain threshold for damage initiation and linear evolution of the damage with the accumulated plastic strain leads to the following equation for damage evolution:
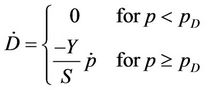 (6)
(6)
where  is the accumulated plastic strain threshold and S is the damage resistance parameter, which are material dependent properties. For the uniaxial stress state, and assuming that the elastic strain can be neglected in comparison to the total strain, the accumulated plastic strain can be considered equal to the principal strain. The damage increases until it reaches a critical value
is the accumulated plastic strain threshold and S is the damage resistance parameter, which are material dependent properties. For the uniaxial stress state, and assuming that the elastic strain can be neglected in comparison to the total strain, the accumulated plastic strain can be considered equal to the principal strain. The damage increases until it reaches a critical value  which can be calculated with the following equation [10]:
which can be calculated with the following equation [10]:
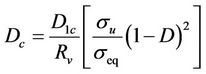 (7)
(7)
where 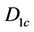 is the critical damage for the uniaxial stress state and can be measured in a tensile test,
is the critical damage for the uniaxial stress state and can be measured in a tensile test, 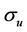 is the ultimate tensile stress and
is the ultimate tensile stress and
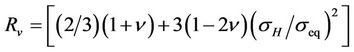
is called triaxiality factor, which accounts for the difference between the actual stress state and the perfectly uniaxial stress state.
This model was later implemented in the Abaqus/Explicit solver using the VUMAT subroutine [20] following the numerical algorithm proposed by Lee and Pourboghrat [21].
3. Experimental Procedure
In order to determine mechanical properties and damage parameters, standard tensile tests were carried out for specimens of SAE 1050 steel for the lamellar and for the spheroidized microstructures. Three specimens for the hot rolled ferrite-pearlite material and nine specimens for the spheroidized material were tested.
The spheroidized material has been cold rolled, with a thickness reduction of 50% and subsequently annealed at 700˚C for 13 hours in a 100% H2 atmosphere, to obtain the characteristic spheroidized microstructure. The specimens were machined from a 1.0 mm thickness sheet (spheroidized material) and from a 2.0 mm thickness sheet (hot rolled material. The neck section had 75 mm length and 12.5 mm width, as shown in Figure 1.

Figure 1. Workpiece dimensions, in mm, for the tensile test.
The damage variables were calculated using the variation of the elastic modulus, so several loading-unloading cycles were needed in order to measure this property with strain increase. The tests were performed in an Instron 3369 universal testing machine, with a 50 kN load cell. Each cycle began with a 1 mm crosshead displacement followed by an unloading until the force attained 50 N. The crosshead velocity was fixed at 2 mm/min. The strains were measured through a clip gage extensometer with 50 mm gage length. Sampling frequency was 5 Hz. Figure 2 illustrates the experimental setup.
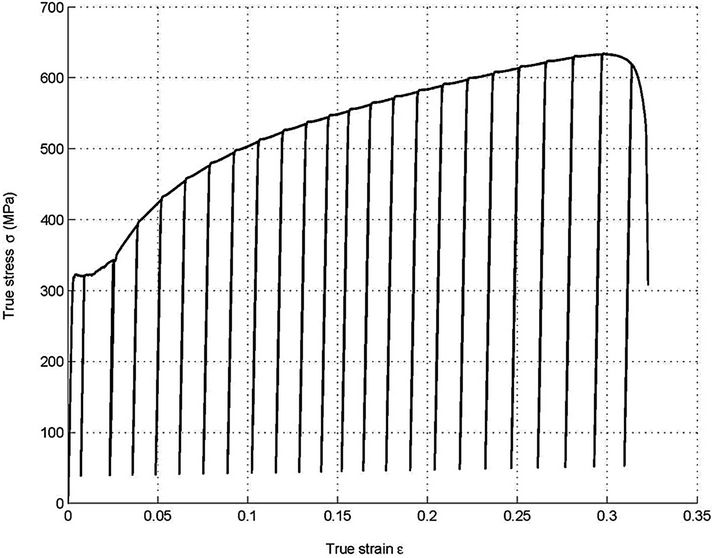
Figure 3 shows the true stress-strain curves for both types of tested specimens. The loading-unloading cycles shown were used in the evaluation of the elastic modulus, measured always during the unloading path, following recommendations by Lemaitre [10]. The drop in the true stress, as pictured in this figure, can be linked to the fracture initiation. To represent the work hardening behavior of the material, Ludwik equation [22] has been used, as presented by Equation (8). The material constants are given in Table 1.
 (8)
(8)
The evolution of the elastic modulus is shown in Figure 4 for the tested materials (including the pure iron results [23] and other carbon steels [24,25] obtained from the literature). It may be observed that the elastic modulus decreases with increasing carbon level. Also, there is a significant non-linear drop in the elastic modulus for small strains, followed by a linear evolution. Lemaitre’s model considers that the damage does not occur for a strain below the critical value, and will grow with a constant rate after that value. For this reason, following the same procedure of Celentano et al. [24], any elastic modulus degradation below the linear part of the curve will be neglected. This transition coincides with the transition of the elastic regime to the plastic behavior of the material. Therefore, yielding strain will be considered as the damage strain threshold and the elastic modulus, at this point, will be assumed to be the one for the undamaged material.
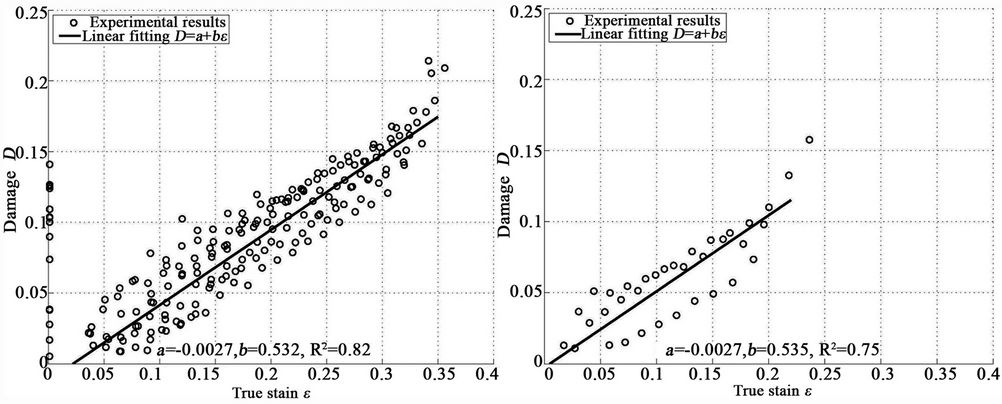
The damage evolution, measured trough Equation (3), is shown in Figure 5 for both studied alloys. Critical damage  is taken as the damage value prior to the non-linear increase in damage, just before fracture. The
is taken as the damage value prior to the non-linear increase in damage, just before fracture. The
 (a)
(a) (b)
(b)
Figure 2. Experimental setup for the tensile tests.
other parameter to be evaluated is the damage resistance S, calculated trough Equation (9), which is obtained by manipulating Equation (6) and assuming that in the tensile test the material is under a perfectly uniaxial stress state.
 (9)
(9)
To obtain the value of S, several experimental points must be taken from Figures 3 and 5 for different strains.
Table 1 summarizes the mechanical and damage parameters identified for SAE 1050 steel for both microstructural conditions.
It must be pointed out that these parameters can be used as inputs for finite element simulations of the tensile test.
4. Numerical Simulations
Lemaitre’s model was implemented in Abaqus/Explicit finite element solver using a VUMAT subroutine aiming at the coupling of isotropic plasticity with damage, based on the stress integration algorithm called operator-split.
For each time step, the incremental strain was considered as being fully elastic, and then the corresponding stress tensor was evaluated. The von Mises criterion, coupled with damage, was used to determine if the material is indeed below the yielding condition:
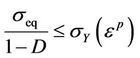 (9)
(9)
If Equation (10) is not satisfied, then a plastic correcting procedure must be used to calculate the plastic increment and ensure the consistency condition. Details of this plastic corrector can be found in Lee and Pourboghrat [22]. After this calculation, stresses, the damage variable and the plastic strain are updated for the next step. Further details may be obtained in Tsiloufas [26].
The tensile test was simulated using an imposed longitudinal displacement on the right end of the specimen, with the same 2 mm/min velocity as for the experimental procedure. Boundary conditions of restricted transversal
 (a)
(a)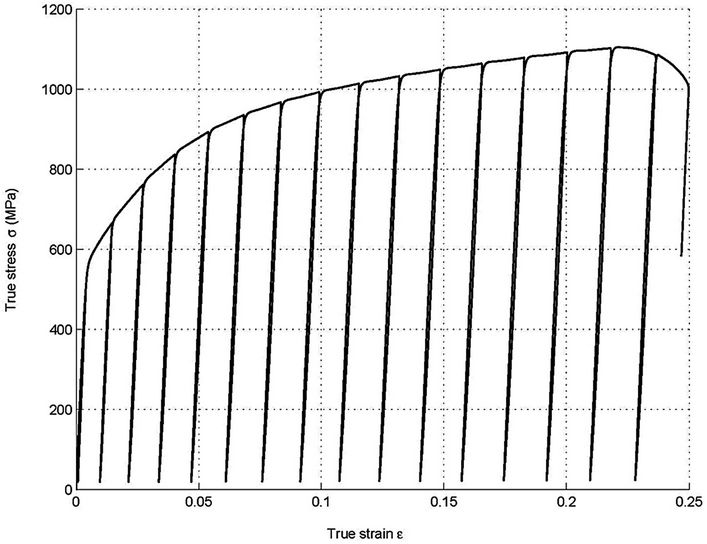 (b)
(b)
Figure 3. True stress-strain curves for SAE 1050 steel. (a) Spheroidized alloy, (b) Hot rolled alloy.
and normal displacement were imposed for both ends of the specimen, simulating the jaws of the tensile test equipment. The mesh in the test region is formed by 4500 solid hexahedral elements, with 8 nodes, linear integration and 0.5 mm length.
Figure 6 shows the resulting true stress-strain curves. The numerical simulations could properly reproduce the work hardening behavior of the tested materials, however the difference between the effective stress  , that is measured through the load cell
, that is measured through the load cell
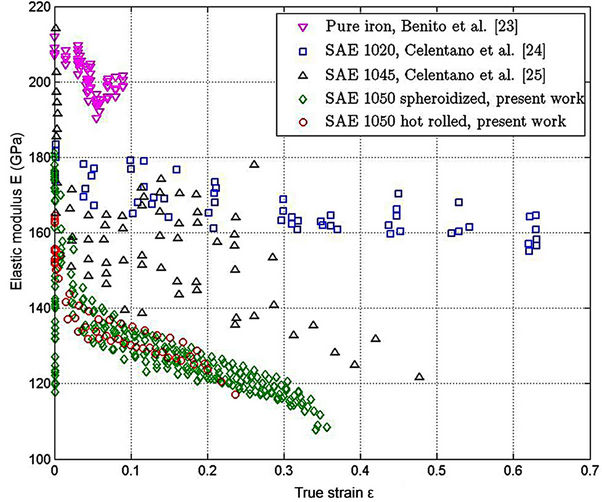
Figure 4. Elastic modulus evolution for SAE 1050 steel and comparison with pure iron and other carbon steels [23-25].
 (a) (b)
(a) (b)
Figure 5. Ductile damage evolution versus true strain for SAE 1050. (a) Spheroidized alloy, (b) Hot rolled alloy.
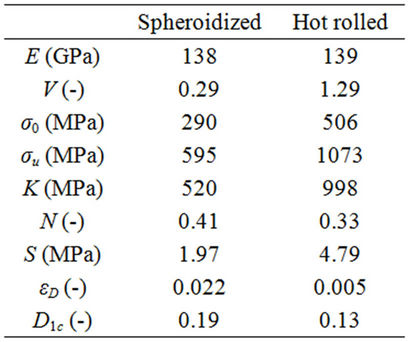
Table 1. Mechanical and damage parameters for SAE 1050 steel
in the experiments, and the real stress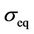 , must be pointed out. This may be explained by observing the material work hardening curve in terms of the real stress reaching saturation, due to the damage increase, which diminishes the material’s area of resistance.
, must be pointed out. This may be explained by observing the material work hardening curve in terms of the real stress reaching saturation, due to the damage increase, which diminishes the material’s area of resistance.
In more detail, damage evolution is shown in Figure 7. It may be observed that damage does not evolve in a linear way, as expected by Lemaitre’s theory. This can be explained observing Figure 8, which shows the evolution of the triaxiality factor . Lemaitre’s model considers that the stress state in a tensile test is perfectly uniaxial, which is not true, as the value of
. Lemaitre’s model considers that the stress state in a tensile test is perfectly uniaxial, which is not true, as the value of  grows for
grows for
 (a)
(a) (b)
(b)
Figure 6. Strain hardening curves for SAE 1050. Experimental and numerical results. (a) Spheroidized alloy, (b) Hot rolled alloy.
strains higher than 0.15.
Figures 9 and 10 shows the damage contour evolution for both alloys, along with a picture of the fractured experimental specimen. The fracture in the experimental test does not occur in the middle part of the sample, because any imperfection in the manufacturing of the workpiece or in the setup of the experiment may change the fracture position. It may be observed that damage is localized in the region near to the fracture, which is expected, since the localization of the strain occurring in the necking zone is the main responsible for the damage accumulation.
5. Damage Behavior for Carbon Steel Alloys
Using data from Refs. [24,25], Figure 11 summarizes the
 (a) (b)
(a) (b)
Figure 7. Damage evolution with strain for SAE 1050. Experimental and numerical results. (a) Spheroidized alloy, (b) Hot rolled alloy.

Figure 8. Evolution of the triaxiality factor for both tested materials.
damage evolution in a tensile test for SAE 1020 and for 1045 steels and those of the present research. It is possible to notice that the strain threshold for damage initiation decreases and the damage growth increases with increasing carbon levels. The reason behind this fact can be associated to the microvoid formation in ductile fracture, which nucleates and grows at the interface between the ferrite matrix and the harder second phase particles [27], whose amount is proportional to the carbon level. Also, the microstructure seems to act mostly on the value of the critical damage, since for both tested SAE 1050 steels, damage initiates and increases in a similar fashion, although they present different critical damage values.
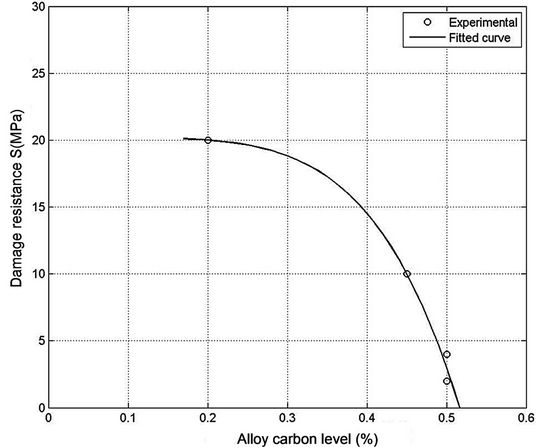
For practical/industrial purposes, it is interesting to suggest a curve fitting for both damage resistance S and the damage strain threshold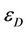 , as a function of the carbon level for SAE 10XX steels. Results are shown in Figure 12. A power law of the form
, as a function of the carbon level for SAE 10XX steels. Results are shown in Figure 12. A power law of the form , with constants given in Table 2, has been chosen because of good agreement with experimental points.
, with constants given in Table 2, has been chosen because of good agreement with experimental points.
These curves can be used as guidelines for numerical simulations in industry as a first approximation in a basic project. The uniaxial critical damage  can be calculated using the empiric relationship of Lemaitre [10]:
can be calculated using the empiric relationship of Lemaitre [10]:
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f) (g)
(g)
Figure 9. (a)-(f) Damage contour evolution (g) fractured experimental specimen. Spheroidized SAE 1050 steel.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f) (g)
(g)
Figure 10. (a)-(f) Damage contour evolution (g) fractured experimental specimen. Hot rolled SAE 1050 steel.

Figure 11. Damage evolution for carbon steel alloys.
 (a)
(a)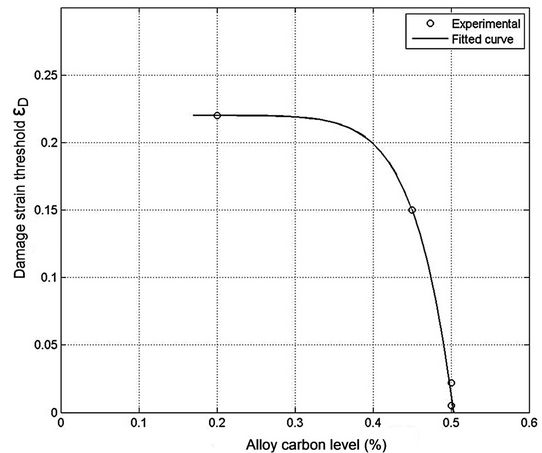 (b)
(b)
Figure 12. Power law fitting for damage properties as a function of the carbon level in SAE 10XX steels. (a) Damage resistance, (b) Damage strain threshold.
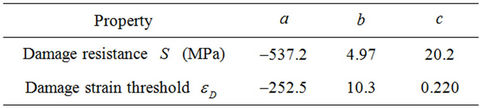
Table 2. Power law constants for damage parameters as a function of carbon level for SAE 10XX steels.
 (10)
(10)
where  is the engineering fracture stress and
is the engineering fracture stress and  is the ultimate tensile engineering stress, both parameters easily provided by steel manufacturers. A comparison between the estimated and the measured value for uniaxial critical damage is shown in Table 3.
is the ultimate tensile engineering stress, both parameters easily provided by steel manufacturers. A comparison between the estimated and the measured value for uniaxial critical damage is shown in Table 3.
Although these guidelines can be useful, a parameter characterization procedure similar to the one here presented is highly recommended, for a more precise result.
6. Conclusions
In the present work, a continuum damage characterization study using loading-unloading cycles during tensile testing was performed for SAE 1050 steel for two microstructural conditions: heat-treated spheroidized cementite

Table 3. Measured and estimated uniaxial critical damage for SAE 1050 steel.
and lamellar ferrite-pearlite (hot rolled). Damage itself was indirectly measured by means of the degradation of the elastic modulus. Mechanical parameters for modeling the work hardening, behavior and the damage evolution were evaluated for the Lemaitre’s ductile damage model.
A numerical algorithm was written to account for the coupling between damage and isotropic plasticity, and implemented in Abaqus/Explicit solver by means of a VUMAT subroutine. Then, simulations of the tensile test were performed, providing good agreement with experimental results. The difference between effective stresses and the real stresses acting on a damaged volume element is presented. Numerical damage evolution was not linear with strain, as would be expected. The explanation lies on the stress-state, which ceases to be perfectly uniaxial for a strain higher than about 0.15.
Although damage mechanics cannot describe macrocrack formation that takes place just prior to fracture, using such a model together with experimental characterization procedure seem to be a useful manner for predicting the initial stages of a ductile failure phenomenon.
7. Acknowledgements
The authors would like to thanks Brasmetal Waeholtz for providing the material samples for the tests, GMSIEPOLI/USP for the tensile test machine and CAPES for the scholarship of SPT, provided for the development of this study.
REFERENCES
- M. G. Cockroft and D. J. Latham, “Ductility and the Workability of Metals,” Journal of the Institute of Metals, Vol. 96, 1968, pp. 33-39.
- M. Oyane, T. Sato, K. Okimoto and S. Shima, “Criteria for Ductile Fracture and Their Applications,” Journal of Mechanical Working Technology, Vol. 4, No. 1, 1980, pp. 65-81. doi:10.1016/0378-3804(80)90006-6
- A. L. Gurson, “Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media,” Journal of Engineering Materials and Technology, Vol. 99, No. 1, 1977, pp. 2-15. doi:10.1115/1.3443401
- L. M. Kachanov, “Rupture Time under Creep Conditions,” International Journal of Fracture, Vol. 97, 1999, pp. 11-18.
- J. L. Chaboche, “Continuum Damage Mechanics: Present State and Future Trends,” Nuclear Engineering and Design, Vol. 105, No. 1, 1987, pp. 19-33. doi:10.1016/0029-5493(87)90225-1
- J. Lemaitre, “How to Use Damage Mechanics,” Nuclear Engineering and Design, Vol. 80, No. 1, 1984, pp. 233- 245. doi:10.1016/0029-5493(84)90169-9
- J. Lemaitre, “A Continuous Damage Mechanics Model for Ductile Fracture,” Journal of Engineering Materials and Technology, Vol. 77, 1985, pp. 335-344.
- J. L. Chaboche, “Continuum Damage Mechanics: Part I— General Concepts,” Journal of Applied Mechanics, Vol. 55, No. 1, 1988, pp. 55-64. doi:10.1115/1.3173661
- J. L. Chaboche, “Continuum Damage Mechanics: Part II— Damage Growth, Crack Initiation and Crack Growth,” Journal of Applied Mechanics, Vol. 55, No. 1, 1988, pp. 65-72. doi:10.1115/1.3173662
- J. Lemaitre, “A Course on Damage Mechanics,” 2nd Edition, Springer, Berlin, 1996. doi:10.1007/978-3-642-18255-6
- C. L. Chow and J. Wang, “An Anisotropic Theory of Continuum Damage Mechanics for Ductile Fracture,” Engineering Fracture Mechanics, Vol. 27, No. 5, 1987, pp. 547-558. doi:10.1016/0013-7944(87)90108-1
- W. Tai and B. Yang, “A New Damage Mechanics Criterion for Ductile Fracture,” Engineering Fracture Mechanics, Vol. 27, No. 4, 1987, pp. 371-378. doi:10.1016/0013-7944(87)90174-3
- T.-J. Wang, “Unified CDM Model and Local Criterion for Ductile Fracture: I—Unified CDM Model for Ductile Fracture,” Engineering Fracture Mechanics, Vol. 42, 1992, pp. 177-183.
- T.-J. Wang, “Unified CDM Model and Local Criterion for Ductile Fracture: II—Ductile Fracture Local Criterion Based on the CDM Model,” Engineering Fracture Mechanics, Vol. 42, 1992, pp. 185-193.
- S. Chandrakanth and P. Pandey, “An Isotropic Damage Model for Ductile Material,” Engineering Fracture Mechanics, Vol. 50, No. 4, 1995, pp. 457-465. doi:10.1016/0013-7944(94)00214-3
- N. Bonora, “A Nonlinear CDM Model for Ductile Failure,” Engineering Fracture Mechanics, Vol. 58, No. 1, 1997, pp. 11-28. doi:10.1016/S0013-7944(97)00074-X
- L. Storojeva, D. Ponge, R. Kaspar and D. Raabe, “Development of Microstructure and Texture of Medium Carbon Steel during Heavy Warm Deformation,” Acta Materialia, Vol. 52, No. 8, 2004, pp. 2209-2220. doi:10.1016/j.actamat.2004.01.024
- F. A. McClintock, “A Criterion for Ductile Fracture by the Growth of Holes,” Journal of Applied Mechanics, Vol. 35, No. 2, 1968, pp. 363-371. doi:10.1115/1.3601204
- F. Sidoroff, “On the Formulation of Plasticity and Viscoplasticity with Internal Variables,” Archiwum Mechaniki Stosowanej, 1975, pp. 807-819.
- Simulia Abaqus 6.10, “User Subroutines Reference Manual,” 2010.
- S. W. Lee and F. Pourboghrat, “Finite Element Simulation of the Punchless Piercing Process with Lemaitre Damage Model,” International Journal of Mechanical Sciences, Vol. 47, No. 11, 2005, pp. 1756-1768. doi:10.1016/j.ijmecsci.2005.06.009
- P. Ludwik, “Elements der Technologischen Mechanik,” 3rd Edition, Vol. 32, Springer, Berlin, 1909.
- J. A. Benito, J. M. Manero, J. Jorba and A. Roca, “Change of Young’s Modulus of Cold-Deformed Pure Iron in a Tensile Test,” Metallurgical and Materials Transactions A, Vol. 36A, 2005, pp. 3317-3324.
- D. J. Celentano and J.-L. Chaboche, “Experimental and Numerical Characterization of Damage Evolution in Steels,” International Journal of Plasticity, Vol. 23, No. 10-11, 2007, pp. 1739-1762. doi:10.1016/j.ijplas.2007.03.008
- D. J. Celentano, P. E. Tapia and J. L. Chaboche, “Experimental and Numerical Characterization If Damage Evolution in Steels,” In: G. Buscaglia, E. Dari and O. Zamonsky, Eds., Mecánica Computacional, Vol. XXIII, Bariloche, Argentina, 2004, pp. 45-58.
- S. P. Tsiloufas, “Estudo da Fratura Dúctil em Chapas de Médio Carbono Sob a Ótica da Teoria da Mecânica do Dano (in Portuguese),” MSc. Dissertation, University of São Paulo, São Paulo, 2012.
- J. Gurland, “Observations on the Fracture of Cementite Particles in a Spheroidized 1.05% C Steel Deformed at Room Temperature,” Acta Metallurgica, Vol. 20, No. 5, 1972, pp. 735-741. doi:10.1016/0001-6160(72)90102-2
NOTES
*Corresponding author.

