Circuits and Systems
Vol.07 No.04(2016), Article ID:65477,9 pages
10.4236/cs.2016.74015
Harmonic Reduction in Wind Power Generating System Using Shunt Active Filter with SPWM Technique
R. Zahira1, A. Peer Fathima2, Ranganath Muthu3
1Department of Electrical and Electronics Engineering, Tagore Engineering College, Chennai, India
2School of Electrical Engineering, Vellore Institute of Technology, Chennai, India
3Department of Electrical and Electronics Engineering, SSN College of Engineering, Kalavakkam, Chennai, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 March 2016; accepted 10 April 2016; published 13 April 2016
ABSTRACT
Due to environmental conditions, the wind power generation is fluctuating in nature. This affects the electrical network interconnected with these systems. When the wind power generators are connected to the nonlinear loads, there is distortion in the waveform. These distortions should be within limits according to national and international guidelines framed for power quality. This paper presents a mitigation technique with a shunt active filter, which reduces harmonic distortion to the permitted limit. Sine pulse width modulation (SPWM) control scheme is used to control shunt active filter. This technique eliminates harmonic distortion and maintains unity power factor. The simulation for proposed method is carried out using MATLAB/SIMULINK and results are validated.
Keywords:
Wind Power Generation, SPWM, Shunt Active Filter, Harmonic, Power Quality

1. Introduction
There is fast growth in wind power generation systems. To keep the generator torque constant in the presence of wind speed fluctuations, modern wind turbines use variable speed drives [1] . The penetration of wind energy in the grid raises the compatibility of the wind turbine power production with the grid. In particular, the contribution to grid stability, power quality and behavior during fault situations plays an important role as the reliability [2] . Wind energy is not a constant source of energy. It varies continuously and gives energy in sudden bursts. About 50% of the entire energy is given out in just 15% of the operating time. Wind strengths vary and thus there cannot be any guarantee of continuous power. Equation (1) gives power extracted from the wind.
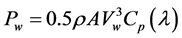 (1)
(1)
where, Pw is extracted power from the wind, ρ is air density (approximately 1.2 kg/m3 at 20˚C at sea level), Vw is the wind velocity (m/s) (velocity can be controlled between 3 to 30 m/s), and Cp = the power coefficient, which is a function of both tip speed ratio (λ) and blade pitch angle β (deg.) [3] .
The power electronics converter plays an important role in modern wind energy conversion system (WECS) for variable speed control method [4] . The nonlinear loads, which are connected to system, are the main sources of harmonics, which distort the sinusoidal waveform. To reduce this distortion and improve the quality of power shunt active filters are proposed. A shunt active filter extracts the voltage and current from the system, which is in a-b-c coordinates [5] . From a-b-c coordinates, it is converted to d-q coordinate and the reference signal is generated using the proposed SPWM control technique [6] . SPWM technique is based on the variable index and the integral of the output signal provided from the phase detection stage. The obtained triangular signal contains the information related to the output signal and its amplitude will vary in proportion to the amplitude of the reference signal. This is a very simple technique for harmonic reduction. In this technique, the pulse magnitude will be constant and only the pulse time (width) can be changed. In this, a pure sine wave is compared with a carrier (triangular), which produces gate pulses. Sine wave has fundamental frequency and carrier wave can be taken more than fundamental frequency.
In this paper, analysis of harmonics present in a variable speed WECS with doubly fed induction motor is done and to mitigate these harmonics, shunt active filter (SAF) with a SPWM control technique is used. These mitigations should satisfy the international standards limit IEEE 519-1992. The paper is organized as follows: In the next section shunt active filter is discussed. The proposed SPWM control technique is described in Section 3. The simulation results are presented in Section 4. Finally, Section 5 gives the conclusion.
2. Shunt Active Filter
The proposed three-phase active power filter consists of a power converter, a DC-link capacitor and a filter inductor. To eliminate current harmonic Components generated by nonlinear loads, the active power filter produces equal but opposite harmonic currents to the point of connection with the nonlinear load. This results in a reduction of the original distortion and correction of the power factor. For the sake of simplicity, in the calculation of reference currents and description of the control scheme, the reference frame transformation method will be used [7] .
The more usual active power filter (APF) configuration is connected in shunt at the point of common coupling to inject the current harmonics. To cancel the harmonics and compensate the reactive power, an active power filter is the suitable solution [8] . The APF concept uses an inverter to inject currents or voltage harmonic components to cancel the load harmonic components; it is also called as Active Power Line Conditioners (APLC). This filter can be installed in a low voltage power system to compensate one or more loads. Thus, it avoids the transmission of current harmonics in the system [9] . The enhancements of different control strategies give APF to a new location. Gyugyi and Strycula first introduced the concept of shunt APLC in 1976. Figure 1 shows the overall block diagram of wind energy system connected to the grid and non-linear load along with APF.
The voltage source inverter should be controlled in such a way as to generate the voltages, which are same as the reference voltages generated, by the detection and control block. Here in this work, sinusoidal pulse width modulation (SPWM) is used as the switching strategy for the inverter. Actually, any PWM technique can be used as the switching strategy for the VSI.
3. Sine Pulse Width Modulation
Actually, any PWM technique can be used as the switching strategy for the VSI. However, due to constant switching frequency, the SPWM technique has been chosen to control the VSI. The following reasons will justify the selection of SPWM as the control strategy for the VSI.
1) The output of the inverter should be same as the reference voltages generated by the detection and control block.
Figure 1. Wind power generation with shunt active filter.
2) From the theory of SPWM [9] , we know that the fundamental of the output of the inverter will be same as the modulating waveform used to compare the triangular carrier.
Combining (1) and (2) it can be concluded that if the reference voltages generated by the detection and control block are given as the modulating waveforms for the inverter then the fundamental component of the output of the inverter will be same as the reference voltages generated by the detection and control block [10] . This inherent advantage of SPWM (which makes the design much simpler) justifies the selection of SPWM as the switching strategy for the inverter. Along with this, the SPWM technique also has advantage of very high modulation frequency, which in turn reduces the filter requirement [8] .
The switches in the voltage source inverter can be turned on and off as required. In the simplest approach, the top switch is turned on and off only once in each cycle, resulting in a square wave waveform. However, if turned on several times in a cycle an improved harmonic profile may be achieved.
In the most straightforward implementation, generation of the desired output voltage is achieved by comparing the desired reference waveform (modulating signal) with a high-frequency triangular “carrier” wave, as depicted schematically in Figure 2. Depending on whether the signal voltage is larger or smaller than the carrier waveform, either the positive or the negative DC bus voltage is applied at the output. Note that over the period of one triangle wave, the average voltage applied to the load is proportional to the amplitude of the signal (assumed constant) during this period [11] .
The resulting chopped square waveform contains a model of the desired waveform in its low frequency components, with the higher frequency components being at frequencies close to the carrier frequency.
The root mean square value of the AC voltage waveform is still equal to the DC bus voltage, and hence the PWM process does not affect the total harmonic distortion. The harmonic components are merely shifted into the high frequency range and are automatically filtered due to inductances in the AC system.
When the modulating signal is a sinusoid of amplitude Am, and the amplitude of the triangular carrier is Ac, the ratio m = Am/Ac is known as the modulation index. The modulation index controls the amplitude of the applied output voltage [12] . With a sufficiently high carrier frequency (drawn for fc/fm = 21 and t = L/R = T/3; T = period of fundamental), the high frequency components do not propagate significantly in the ac network (or load) due the presence of the inductive elements. However, a higher carrier frequency does result in a larger number of switching per cycle and hence in an increased power loss. Typically switching frequencies in the 2 - 15 kHz range is considered adequate for power systems applications. Figure 2 shows the principle of pulse width modulation generated by SPWM technique. In this control technique, the triangular wave is compared to desired waveform and pulse is generated accordingly.
By using the SPWM technique, the switching losses are reduced, utilization of DC power supply to deliver a higher output voltage with the same DC supply is good, good linearity in voltage and current control, and reduced harmonic contents in the output voltage and current, especially in the low-frequency region [13] .
Figure 2. Principle of pulse width modulation technique.
4. Simulation Analysis
The simulation model of wind energy generation system with the DFIG is shown in Figure 3. This is constructed in the MATLAB/SIMULINK environment with the variable wind speed and connected to non-linear load. Due to variation of speed, the output will be more distorted as shown in Figure 4. The total harmonic distortion (THD) is measured with FFT analysis in matlab and is noted as 24.70%. This distortion level exceeds the harmonics standard IEEE 519-1992. Figure 5 illustrates the real and reactive power generated by the wind energy system connected to the grid. The reactive power is oscillatory for wind-generated system. The SAF connected to the system will compensate the both the harmonic distortion and reactive power oscillation.
To mitigate the distortions created by the non-linear load, the shunt active filter is used for compensation. The shunt active filter in turn controlled by the SPWM control scheme. This control scheme is used as the switching strategy for the inverter. Figure 6 shows the voltage and current in a-b-c coordinates tapped from the point of common coupling (PCC). Then a-b-c to d-q-o transformation is done. The d-q-o transform is often referred to as Park’s transformation. In the case of balanced three-phase circuits, application of the d-q-o transform reduces the three AC quantities to two DC quantities. Simplified calculations can then be carried out on these DC quantities before performing the inverse transform to recover the actual three-phase AC results. It is often used in order to simplify calculations for the control of three-phase inverters. After simplifying to d-q coordinate, the SPWM controller generates compensating pulse as shown in Figure 7. These pulses control the inverter according to the distortion created in the line. Then the inverter output signal is fed back into line. By this way, the distorted waveform is compensated.
After connecting the shunt active filter to the line, the distortion is reduced, as shown in Figure 8 & Figure 9. Figure 8 shows the voltage waveform and Figure 9 the current waveform. THD is measured for the current waveform and it is seen in Figure 10 that the harmonics level is reduced to 2.54%, which is within the acceptable limit. Figure 11 gives the real and reactive power after compensation. It is seen that the reactive power has a lower settling time.
Figure 3. Wind generation system connected to non-linear load.
Figure 4. THD of the system without compensation.
Figure 5. Real and reactive power of the system before compensation.
Figure 6. Wind generation system with compensation.
Figure 7. Inverter pulse from SPWM.
Figure 8. Voltage waveform with filter.
Table 1 summarizes the results from the simulation. The harmonic order of 3rd, 5th 7th, 11th and 13th creates THD of 0.19%, 22%, 8.46%, 5.79% and 3.3% respectively. After compensation, the THD is reduced to 0.31%,
Figure 9. Current waveform with filter.
Figure 10. THD of the system with compensation.
Figure 11. Real and reactive power after compensation.
2.15%, 0.96%, 0.63% and 0.29% respectively.
Table 2 summarizes the overall harmonics created by the system, which is 24.70% before connecting the SAF is reduced to 2.54% after connecting SAF. It is also illustrated that power factor is improved from 0.815 to 0.992, which is close to unity after compensation.
Figure 12 graphically compares the THD’s, in which the graph without filter has higher THD level. After connecting the filter, the THD is reduced, satisfying the harmonic standards.
5. Conclusions
The wind energy is fluctuating in nature and creates distortion in the waveform when connected to the grid with loads it. In this paper, the model of wind energy generation systems interfaced with the grid was analysed and computationally simulated in MATLAB/Simulink. The waveform is analysed with FFT window, which has the THD value of 24.70% and is not within the standard limit. To mitigate this distortion and reduce it to the permissible limit, this paper proposes the use of shunt active filter with SPWM control technique.
By connecting the SAF, the quality of power to the grid and the non-linear load is considerably increased. The shunt active filter has the capability to compensate the harmonic distortion and keep it within the prescribed standard limit. With the help of the SPWM technique, the switching losses are reduced, utilization of DC power supply to deliver a higher output voltage is higher, good linearity in voltage and current control is achieved,
Table 1. THD based on harmonic order.
Table 2. Harmonic distortion and power factor comparison.
Figure 12. Graphical representation of THD reduction.
reduces harmonic contents in the output voltage and current, especially in the low-frequency region. From the results, it is shown that the THD level with SAF is reduced to 2.54% from its original value 24.70%. Also, a near unity power factor is achieved in this case.
Cite this paper
R. Zahira,A. Peer Fathima,Ranganath Muthu, (2016) Harmonic Reduction in Wind Power Generating System Using Shunt Active Filter with SPWM Technique. Circuits and Systems,07,157-165. doi: 10.4236/cs.2016.74015
References
- 1. Gawain, L., Tiwari, H. and Bansal, R.C. (2013) Improving Power Quality of Wind Energy Conversion System with Unconventional Power Electronic Interface. International Journal of Electrical Power & Energy Systems, 44, 445-453.
http://dx.doi.org/10.1016/j.ijepes.2012.07.051 - 2. Kesraoui, M., Chaib, A., Meziane, A. and Boulezaz, A. (2014) Using a DFIG Based Wind Turbine for Grid Current Harmonics Filtering. Energy Conversion and Management, 78, 968-975.
http://dx.doi.org/10.1016/j.enconman.2013.07.090 - 3. Hoseinpour, A., Barakati, S.M. and Ghazi, R. (2012) Harmonic Reduction in Wind Turbine Generators Using a Shunt Active Filter Based on the Proposed Modulation Technique. International Journal of Electrical Power & Energy Systems, 43, 1401-1412.
http://dx.doi.org/10.1016/j.ijepes.2012.06.052 - 4. Gaillard, A., Poure, P., Saadate, S. and Machmoum, M. (2009) Variable Speed DFIG Wind Energy System for Power Generation and Harmonic Current Mitigation. Renewable Energy, 34, 1545-1553.
http://dx.doi.org/10.1016/j.renene.2008.11.002 - 5. Nian, H., Quan, Y. and Hu, J. (2012) Improved Control Strategy of DFIG-Based Wind Power Generation Systems Connected to a Harmonically Polluted Network. Electric Power Systems Research, 86, 84-97.
http://dx.doi.org/10.1016/j.epsr.2011.12.006 - 6. Kesraoui, M., Chaib, A., Meziane, A. and Boulezaz, A. (2014) Using a DFIG Based Wind Turbine for Grid Current Harmonics Filtering. Energy Conversion and Management, 78, 968-975.
http://dx.doi.org/10.1016/j.enconman.2013.07.090 - 7. Zeng, Z., Yang, H., Zhao, R. and Cheng, C. (2013) Topologies and Control Strategies of Multi-Functional Grid-Connected Inverters for Power Quality Enhancement: A Comprehensive Review. Renewable and Sustainable Energy Reviews, 24, 223-270.
http://dx.doi.org/10.1016/j.rser.2013.03.033 - 8. Melício, R., Mendes, V.M.F. and Catalao, J.P.S. (2011) Comparative Study of Power Converter Topologies and Control Strategies for the Harmonic Performance of Variable-Speed Wind Turbine Generator Systems. Energy, 36, 520-529.
http://dx.doi.org/10.1016/j.energy.2010.10.012 - 9. Anju, R.K. and Chacko, F.M. (2015). An Active Power Filter for Improving the Power Quality of a Distribution Grid. International Journal of Engineering Research and General Science, 3, 875-882.
- 10. Islam, M.S., Raju, N.I. and Ahmed, A.U. (2013) Sinusoidal PWM Signal Generation Technique for Three-Phase Voltage Source Inverter with Analog Circuit & Simulation of PWM Inverter for Standalone Load & Micro-Grid System. International Journal of Renewable Energy Research (IJRER), 3, 647-658.
- 11. Raju, N.I., Islam, M.S., Ali, T. and Karim, S.A. (2013) Study of SPWM Technique & Simulation of Designed Analog Circuit (Op-Amp) Controlled Three-Phase PWM Inverter with Harmonic Reduction. International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, 17-18 May 2013, 1-6.
- 12. Chelladurai, J., Ilango, G.S., Nagamani, C. and Kumar, S.S. (2008) Investigation of Various PWM Techniques for Shunt Active Filter. International Journal of Electrical Systems Science and Engineering, 1, 87-93.
- 13. Singh, N. and Agarwal, V. (2015) A New Random SPWM Technique for AC-AC Converter-Based WECS. Journal of Power Electronics, 15, 939-950.
http://dx.doi.org/10.6113/JPE.2015.15.4.939














