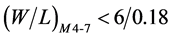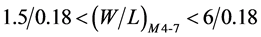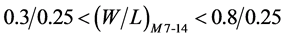Circuits and Systems
Vol.07 No.05(2016), Article ID:66161,10 pages
10.4236/cs.2016.75045
Jitter Reduced Self Biased PLLs― A Systematic Simulation Study
J. Dhurga Devi
Department of ECE, College of Engineering, Anna University, Chennai, India

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 February 2016; accepted 26 April 2016; published 29 April 2016
ABSTRACT
The self biased Phase Locked Loop (PLL) has become a default choice for clock generation in many microprocessors. In today’s scenario, the processor cores are made to operate at rapidly varying combinations of clock frequencies and very low supply voltages. Though the traditional self biased PLL is still being widely used with hardly any modification, it is becoming imperative to take a relook at the design aspects of these PLLs with respect to their jitter performance. This paper presents a systematic simulation study of designing the self biased PLL with the goal of reducing jitter. It further shows that if the self biased PLL is adapted into a dual loop scheme in a systematic manner, a significant jitter improvement can be obtained. Detailed simulations carried out in 0.18 μm CMOS technology indicate a reduction of 56% or more in jitter for the systematically designed dual loop scheme in comparison to the jitter reduced traditional self biased PLL.
Keywords:
Jitter, Dual Loop PLL, Self Biased PLL, Adaptive Bandwidth PLL

1. Introduction
The well proven self biased adaptive bandwidth PLL [1] considers supply and substrate noise as the dominant sources that lead to timing uncertainties of the output clock. Its architecture and loop parameters were optimally designed to make the output clock immune to these noise sources. The Voltage Controlled Oscillator (VCO) employed in this PLL exhibits high gain and facilitates wide operating frequency range for the PLL. Its loop parameters are process insensitive, and therefore the system also becomes process technology independent. These unique features of the self biased PLL ideally are suited for microprocessor clock generation and it has been used for this purpose for nearly two decades [2] - [4] .
However in today’s scenario of tiled and multi core processers, this well proven PLL architecture operates in an environment of rapidly and widely varying combinations of clock frequencies and (low) supply voltages. This is needed in order to meet the overall power envelope constraints [2] - [4] . The processor cores when operated at very high frequencies and low supply voltages are subjected to increasingly more acute jitter constraints. In spite of these severe constraints, the choice of the self biased PLL for microprocessor clock generation is considered “… unchallenged in the foreseeable future due to the wide frequency range required for product binning and power management” [5] .
In this work, a systematic design of these self biased PLLs for jitter reduction is described. The crucial functional blocks that decide the jitter performance, namely the charge pump and the VCO are designed in such a way that the overall jitter contribution is reduced. This design methodology is further extended to a self biased PLL incorporating dual loop scheme to attain significant jitter performance improvement.
Though there have been many papers appearing periodically in the literature addressing the issue of jitter reduction in PLLs, very few of these are in the context of self biased PLLs. In [5] , a delay interpolator based VCO design is proposed with a low gain VCO to provide low jitter while retaining the benefits resulting from bandwidth adaptivity and self biased nature. However this design employs an inverter based delay cell without the use of symmetric loads, and hence lacks the benefit of dynamic supply noise rejection. A calibration technique is proposed in [6] to operate the self biased adaptive bandwidth PLL at various frequency sub bands. In each operating sub band, the VCO gain is designed to be low; thereby this design ensures a low jitter performance. However a systematic approach to jitter reduction has not been addressed in [6] .
Dual loop techniques using conventional oscillators have recently been proposed in [7] - [9] reporting significant reductions in jitter (phase noise) and use a separate loop for coarse frequency acquisition. The present work carries out the systematic design of a similar dual loop scheme for jitter minimization, and closely parallels the work reported in [7] - [9] . But as opposed to using a ring oscillator based PLL as in [7] [8] or an LC oscillator as in [9] , the present work uses the self biased symmetric load VCO based adaptive PLL. Further for the chosen VCO, the appropriate selection of VCO gain for reduced jitter is also discussed. The dual loop technique proposed in [8] , attains jitter improvement by eliminating resistance in the loop filter, instead uses a Multiplying Delay Lock Loop (MDLL) to provide the feed forward path. This MDLL was made to act as fine loop that minimizes ripple and thermal noise generated by the loop filter resistance. This technique [8] discusses about optimization of PLL to PVT variations but a systematic procedure to choose its loop parameters for optimization of jitter performance is not suggested.
The present paper is organized as follows. Section 2 explains the design procedure of the self biased PLL with emphasis on jitter reduction. Detailed simulation results and overall system performance are presented in Section 3 and the conclusions of the present work are given in Section 4.
2. Design of Reduced Jitter Self Biased PLL
The block diagram of the traditional self biased PLL [1] is shown in Figure 1 that includes a Phase Frequency Detector (PFD), Charge Pump (CP1), Loop Filter (LPF), VCO and a Prescalar. It also includes a Bias Generator (BG) to provide bias currents to the charge pump, the PFD as well as the VCO, and this bias current generated adaptively, tracks the operating frequency. The VCO employed is a ring oscillator, and its delay element uses a linearized resistive load enabling the PLL to operate over a wide range of frequencies.
2.1. Impact of System Parameters on Jitter
The jitter performance of the traditional self biased PLL can be normally studied by considering the Noise Transfer Functions (NTFs) and the noise Power Spectral Densities (PSDs) of the various functional blocks of the
Figure 1. Block diagram of self biased PLL.
PLL. The overall PLL output noise PSD 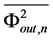 is given by (as given in [10] for e.g.),
is given by (as given in [10] for e.g.),
 (1)
(1)
In the above expression, HCP, HLPF, HVCO and HDIV represent the NTFs of the blocks CP1, LPF, VCO and Prescalar blocks respectively (Figure 1). The quantities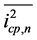 ,
, 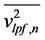 ,
, 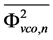 and
and 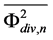 represent the PSD’s of
represent the PSD’s of
the corresponding noise sources. The expressions for the NTFs of the various functional blocks as described in [10] are given in (2)-(5). The purpose of reproducing these equations here is to identify the key parameters that contribute to jitter and to suggest a methodology to reduce jitter.
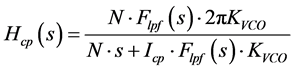 (2)
(2)
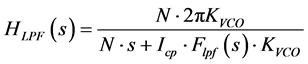 (3)
(3)
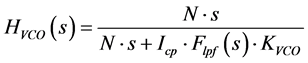 (4)
(4)
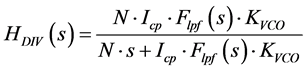 (5)
(5)
In the above expressions, Icp represents the charge pump bias current and N represents the Prescalar divider ratio. 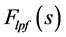 represents the transfer function of first order RC loop filter shown in Figure 1. If one considers the quantities KVCO, Icp, and the loop filter cutoff frequency, it is well known [10] [11] that they strongly influence the NTFs as well the noise PSDs (though the latter dependence is not explicitly shown). Further, the random noise contribution alone is captured in the above equations. Overall jitter also has a systematic component in it, and this is also a function of Icp and KVCO [12] . Further, these latter quantities themselves are intricately related through constraints on loop natural resonant frequency ωn and damping constant ζ given by
represents the transfer function of first order RC loop filter shown in Figure 1. If one considers the quantities KVCO, Icp, and the loop filter cutoff frequency, it is well known [10] [11] that they strongly influence the NTFs as well the noise PSDs (though the latter dependence is not explicitly shown). Further, the random noise contribution alone is captured in the above equations. Overall jitter also has a systematic component in it, and this is also a function of Icp and KVCO [12] . Further, these latter quantities themselves are intricately related through constraints on loop natural resonant frequency ωn and damping constant ζ given by
 (6)
(6)
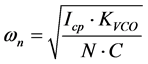 (7)
(7)
Given all the above dependencies, the selection of optimum values of KVCO and Icp for minimizing overall jitter is a non trivial task. Further minimizing overall jitter implies reducing the noise PSDs as well as the NTFs of the various blocks.
Taking up the case of NTFs first, a careful consideration of all the dependencies leads to the following set of assumptions/observations which can aid in the systematic design of a low jitter self biased PLL.
1) Since the original PLL is wideband, it is assumed that the dominant contributor to the overall jitter is the noise originating from the charge pump [10] .
2) A reduction in KVCO leads to a reduction in the charge pump contribution to overall jitter [7] .
3) While reducing KVCO, due consideration must be given to the fact that other factors that are related to it through the PLL loop equations could mitigate the possible improvement in jitter.
4) One possibility for reducing jitter is to reduce KVCO without altering the denominators in (1), and this can be accomplished with a corresponding increase in Icp. This approach is followed in [10] . On the other hand, the work reported in [9] notes this approach as that “… there are practical difficulties which should be kept in mind when employing this strategy in multipath PLLs”. After considering the systematic noise sources like capacitor leakage and charge pump mismatch currents, it is concluded in [9] that KVCO cannot be reduced below a certain limit.
5) Alternatively, one can reduce KVCO and also alter the denominator in (1), which in turn would imply that the system would operate with altered loop parameter values of ωn and ζ. In return for a reduction in overall jitter, these loop parameters can be altered to the extent that the conditions of PLL loop stability and lock time are not degraded significantly. This is the approach followed in the present work and is iteratively designed through simulation so that the reduced jitter does not degrades settling time performance.
Next, taking up the case of the reduction of the noise PSDs of the individual blocks, the dominant noise sources within the key blocks like charge pump and the VCO have to be identified, and then suitably altered to the extant permissible without disturbing the PLL loop dynamics. Considering the VCO first, the circuit diagram of the delay element employed in the self biased PLL [1] is shown in Figure 2. Unlike the symmetric load transistors (M4-M7) and switch transistors (M2-M3), the tail transistor M1 is generally considered to have negligible impact on the overall jitter [13] . Hence, given the overall PLLloop characteristics and NTFs, the sizes of the transistors (M2-M7) have to be chosen such that the VCO noise PSD is reduced while meeting the operating frequency range and VCO gain KVCO. VCO gain of the symmetric load VCO as derived in [1] is given in the below expression (8). In the above equation k stands for the device transconductance of M4 or M7. Ceff represents the effective capacitance that determines oscillator frequency.
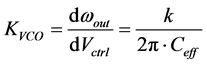 (8)
(8)
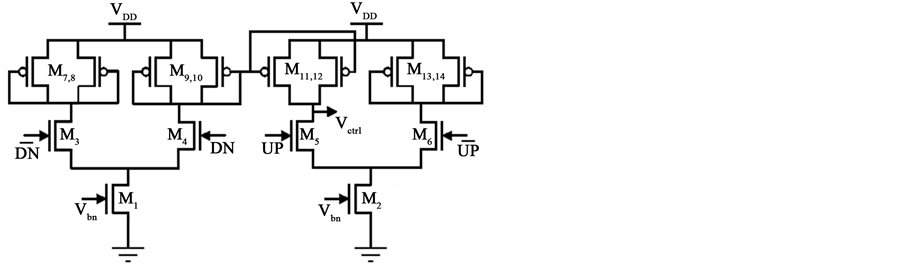
The circuit diagram of the charge pump employed in the self biased PLL is as shown in Figure 3. This architecture is a replica of the delay element, but with the differential switch transistors controlled by UP and DN signals generated by the PFD. Analogous to the delay element, the devices that adversely affect the overall jitter performance are the current source transistors (M7-M14) and switch transistors (M3-M6).
The dimensions of all the jitter sensitive transistors (M2-M7 of Figure 2 and M3-M14, of Figure 3) were chosen through simulations such that the respective block level noise PSDs were minimized while satisfying the overall PLL system level constraints (tuning range of VCO, KVCO and bias currents in the charge pump). But a unique feature in self biased PLL is that the charge pump device dimensions are derived using the delay element device dimensions [1] . This constraint was imposed to mainly minimize charge pump mismatch currents, and implies that fixing the dimensions in the circuit of Figure 2 also fixes those in the circuit of Figure 3.
Figure 2. Circuit schematic of self biased VCO delay element.
Figure 3. Circuit schematic of self biased VCO delay element.
For the traditional self biased PLL, the above mentioned considerations about NTFs and the noise PSDs of the various functional blocks will enable one to (a) size the devices in charge pump and VCO to minimize device noise contribution to jitter and (b) systematically reduce the KVCO and study its impact on jitter. The quantitative results based on simulations will be presented in the next section.
While considering the reduction of KVCO, one cannot reduce KVCO without compromising the capture range and settling time of the traditional self biased PLL. Hence the dual loop scheme [14] is employed and allows one to reduce KVCO without any trade off with capture range and settling time. The principle based on which the traditional single loop self biased PLL is modified into a dual loop scheme to reduce KVCO is briefly discussed next.
2.2. Dual Loop Scheme for Jitter Minimization
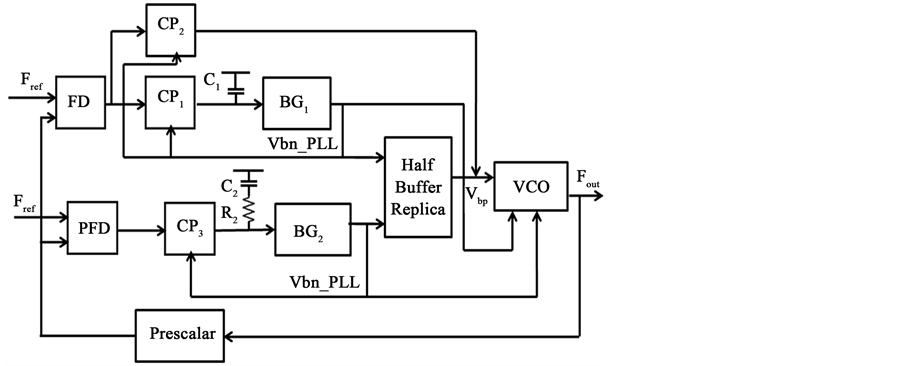
The complete block diagram of the dual loop scheme is shown in Figure 4. The VCO of the self biased PLL has two control inputs. One of the control inputs has a large conversion gain (coarse), provides wide tuning range, and forms part of the Frequency Lock Loop (FLL). The other control input has a low conversion gain (fine) and form part of the PLL. The loop constituting the FLL in Figure 4 comprises of a Quadricorrelator based Frequency Detector (FD), two charge pumps CP1 and CP2, and a bias generator BG1. The charge pump block CP2 in the FLL is used to emulate the resistance in LPF.
The PLL part in the dual loop scheme comprises of the PFD, charge pump CP3, an LPF and a bias generator BG2. The bias current of CP3 is derived from the bias generator BG2. The bias voltages from BG1 and BG2, Vbn_FLL and Vbn_PLL respectively are combined in a half buffer replica stage to generate the bias voltage Vbp for the ring oscillator.
The FLL acquires and brings the output frequency to within the PLL’s capture range. While the FLL tracks the reference frequency, the PLL is disabled by a digital control circuit, and is later enabled when the frequency falls within its capture range. Therefore, under phase lock and very close to phase lock, the entire dual loop system operates only with the PLL being active, and the system reduces to a conventional self biased PLL with a reduced VCO conversion gain.
As was done above the single loop case, the dual loop scheme’s device dimensions of VCO and CP of the PLL part of loop are chosen so as to minimize the respective noise PSDs while satisfying the respective block level specifications. The jitter performance of this systematically designed dual loop is compared with the systematically designed traditional self biased PLL and the results are discussed in the following section.
3. Results and Discussions
All circuit simulations have been carried out using UMC 0.18 μm CMOS technology process libraries. The simulation results are presented in the following order. First, the traditional self biased PLL was designed with the optimum device dimensions of VCO and charge pump functional blocks determined using PNoise analysis in Cadence for reduced jitter performance. The choice of the optimum device dimensions from the PNoise plot is
Figure 4. Block diagram of dual loop self biased PLL.
discussed. Next, the extant of possible improvement in the jitter performance obtained by systematically reducing KVCO of the traditional self biased PLL, is presented. Based on this, the KVCO of the VCO in the PLL is set and accordingly the dual loop self biased PLL is designed. The functionality of the dual loop scheme is verified and the capture transients are presented. The jitter performance of the dual loop is then compared with the jitter reduced traditional self biased PLL employing a high KVCO for the required capture range.
The traditional self biased PLL was designed with the loop parameters ωn/ωref as 1/15 and ζ chosen as 1 respectively. The bias generator was designed for a linear operating range of 0.3 V to 1.1 V that provides control voltage to VCO. For a VCO tuning range of 200 MHz to 3 GHz, KVCO is computed to be 3.5 GHz/V. Based on the KVCO expression given in (6) the ratio of device dimensions of M4-7 to Ceff is defined as given below.
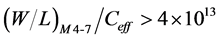
With Ceff chosen as 210 fF, the constraint on dimensions (W/L)M4-7 is set as given below.
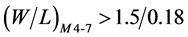
Based on chosen Ceff, the above constraint defines the device dimensions for (W/L)M2-3 as 6/0.18 since capacitance of (W/L)M4-7 and (W/L)M2-3 together contributes Ceff.
The device dimensions of switch transistors (W/L)M2-3 and symmetric load transistors (W/L)M4-7 can be increased from the given constraint of (9)-(10) while satisfying the ratio required to meet the KVCO value. Increasing device dimensions increases Ceff. Hence increasing the device dimensions beyond a range will affect its highest operating frequency. Thus the upper limit on the possible device dimensions that satisfies the operating frequency range is given by the constraint below.

The permissible values of device dimensions of (W/L)M2-3 and (W/L)M4-7, that satisfies KVCO and operating frequency range are given as below
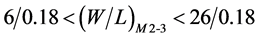
Choosing from these range of device dimensions, there VCO gain characteristics are plotted and are shown in Figure 5. Gain characteristic is plotted for two extreme values and one within the permissible range. The gain remains the same for the three characteristics but for the higher limit in the device dimensions, the highest operating frequency is observed to get limited. Therefore the constraints in (12) define the possible choice of device dimensions of the delay element.
Device dimension of M1 of the delay element is chosen for the required bias current. At the highest frequency of operation the maximum bias current was computed to be 200 μA dependent on the gain and band width value decided in the bias generator. Dependent on this bias current and the respective bias voltage Vbn, the device dimension (W/L) of the tail transistor M1 is computed to be 32/1.
Figure 5. VCO gain characteristic for the three possible choices of device dimensions.
Since the charge pump circuit in the traditional self biased PLL is a replica of the delay element architecture. Therefore for every feasible set of device dimensions in VCO, there is a related device dimension set for the charge pump circuit, which is appropriately scaled by the factor x by which the charge pump current of the self biased PLL is derived from the delay element bias current as described in [1] . The factor x was chosen as 0.2 that sets the ratio between ωn/ωref as 1/15. The permissible range of device dimensions of charge pump circuit thus obtained is given below

In Figure 6, the VCO phase noise characteristic is plotted by progressively increasing the jitter sensitive device dimensions of M2-M7 (of Figure 2) within the permissible range as given in (12). The plots are shown for the extreme limits in the range and one within the permissible range. The noise PSD plots show improvement with increase in device dimensions. This obeys the fact that the resistance of the switch transistors and symmetric load transistors reduces with increase in device dimensions, and hence is the improvement in the noise PSD characteristics.
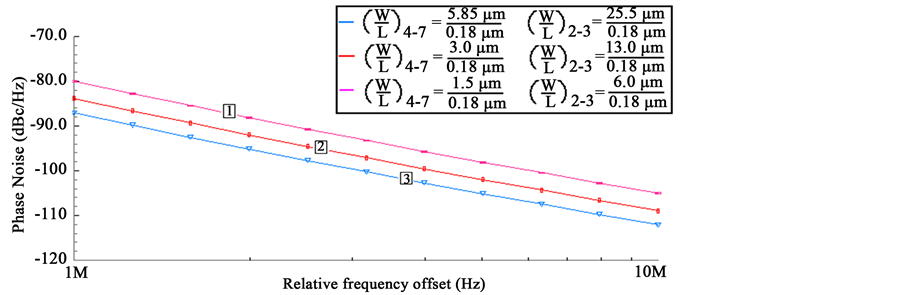
Similarly, in Figure 7, the noise PSDs for charge pump are plotted within the permissible range given in (13) and the plots are given for the extreme limits and one within the permissible range. From the noise PSD plots it can be observed that the lowest noise PSD characteristic corresponds to the lowest device dimensions from the feasible device dimension set. Since these minimum dimensions sets the current source transistors M7-14 with minimum transconductance gm, the output noise current PSD is smallest.
Figure 6. Phase noise plot of VCO at 2100 MHz operating frequency.
Figure 7. Charge pump noise current PSD.
It was observed through simulations that the device sizes corresponding to the plot labeled 1 in Figure 6 and Figure 7 led to the minimum jitter for the traditional single loop self biased PLL and were used for designing VCO and CP circuits while designing the traditional self biased PLL.
Considering the choice of reduced KVCO, its impact on jitter performance was analyzed by simulating the traditional self biased PLL of dual loop system using VCOs with different KVCO settings but with device dimensions (obtained from PNoise plot) that presents minimum noise PSDs. The jitter performance results are given below in Table 1. From the table, it can be noted that the dual loop PLL scales down its jitter performance by the factor by which the KVCO is reduced. This follows with the fact that as KVCO is reduced by certain factor, the impact of systematic noise on output phase noise is also reduced by the same factor. From the different values tabulated, KVCO of 467 MHz/V was chosen for the design of dual loop PLL.
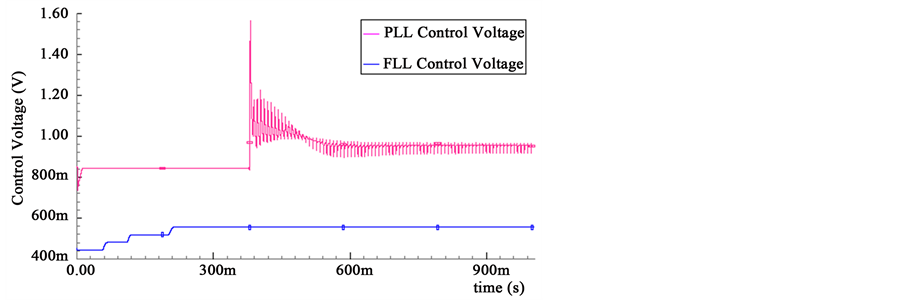
Figure 8 depicts the typical capture transients obtained for the resulting dual loop self biased PLL. The capture transients show the independent tracking nature of FLL and PLL incorporated in the dual loop system. The designed FLL is observed to settle in about 170 ns. The PLL is enabled as the frequency difference is reduced very close to the output frequency (within 4%) and is seen to settle at about 600 ns.
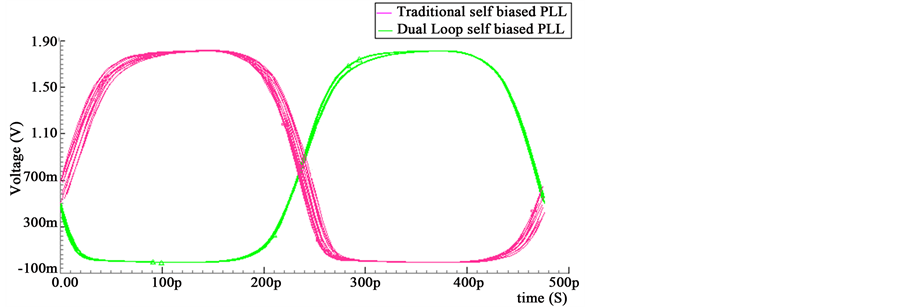
Next, in order to compare the jitter performances of the dual and traditional self biased PLLs, the eye diagram for both cases are plotted in Figure 9 for a nominal output frequency of 2.1 GHz. The RMS jitter computed from this plot was found to be 2.3 pS and 0.5 pS respectively for the traditional and dual loop self biased PLLs, and corresponds to improvement of 77% for the latter.
Two deviations need to be pointed out this stage. First, a KVCO setting of 467 MHz/V is used as against the lowest possible KVCO of 340 MHz/V as given in Table 1. The reason being, for the latter setting, the dual loop VCO settling time was degraded beyond 1 μs, and hence it was avoided. Second, the jitter reduction observed deviates from the prediction of Table 1. This is because Table 1 does not include the noise from the FLL, its bias circuits, and the buffer stages.
A summary of the performance of the present work is provided in Table 2 at the extreme operating frequency of 2700 MHz and a comparison is also provided with those of the dual loop schemes reported recently [6] - [8] .
Figure 8. Capture transients of dual loop PLL at 2100 MHz output frequency.
Table 1. Jitter reduction as a function of KVCO reduction (measured at a frequency of 2100 MHz).
Figure 9. Jitter comparison of traditional self biased PLL with dual loop PLL.
Table 2. Performance comparison at extreme operating frequency.
In terms of jitter and Figure Of Merit (FOM) (as defined in [7] ), it can be seen that dual loop self biased PLL outperforms the traditional self biased PLL and is comparable to the dual loop schemes of [6] - [8] . The acquisition time of the dual loop self biased PLL is found to be inferior compared to the traditional self biased PLL, but still far comparable to that reported in [6] [7] . Although this may not be a fair comparison since the present work is based on simulations only, the main objective here is to identify the key contributing factors and get estimates of the orders of improvements possible. Also, the work reported in [7] lacks supply noise immunity, process immunity and bandwidth adaptivity features that are inbuilt for the self biased PLLs. The jitter performance reported in [8] shows better jitter performance in comparison to the present but had not presented it settling time or power measure. The present work if made to operate with similar KVCO would also have shown comparable jitter performance but with settling time greater than 1 µs.
4. Conclusion
This paper presents a systematic procedure for designing a low jitter self biased PLL based on simulation results. Noise generated from the individual functional blocks was analyzed, and a method was proposed to choose the circuit parameters for jitter reduction. The jitter improvement factor obtained by using a reduced KVCO was determined experimentally through simulation. Two conclusions can be drawn from this simulation study. First is that, in the traditional self biased PLL, the minimum jitter is observed, by using device dimensions that reduce noise PSD from the charge pump and not from the VCO. This leads to the first conclusions that in wide bandwidth PLL, the significant noise contributor is the charge pump circuit. Second is that with KVCO scaled, the PLL bandwidth becomes narrower; the VCO phase noise contribution to the overall phase noise has to increase; and the jitter improvement obtained can be mitigated. Even under this narrow bandwidth condition, a significant jitter performance improvement is observed. Hence it can be concluded that the dominant noise contributor is the charge pump systematic noise, and is observed to get scaled down by the same factor by which the KVCO is reduced. The dual loop technique thus implemented with reduced KVCO shows significant jitter reduction. Although comparison of the present work with silicon implementation results may not be entirely fair, in terms of jitter, lock time and FOM, it was shown that the systematically designed dual loop system performance is either better or comparable to the recently reported work on a ring oscillator based dual loop PLL [7] [8] .
Cite this paper
J. Dhurga Devi, (2016) Jitter Reduced Self Biased PLLs—A Systematic Simulation Study. Circuits and Systems,07,533-542. doi: 10.4236/cs.2016.75045
References
- 1. Maneatis, J.G. (1996) Low-Jitter Process-Independent DLL and PLL Based on Self-Biased Techniques. IEEE Journal of Solid-State Circuits, 31, 1723-1732.
http://dx.doi.org/10.1109/JSSC.1996.542317 - 2. Allen, A., Desai, J., Verdico, F., Anderson, F., Mulvihill, D. and Krueger, D. (2009) Dynamic Frequency-Switching Clock System on a Quad-Core Itanium Processor. IEEE International Solid State Circuits Conference, San Francisco, 8-12 February 2009, 62-63.
http://dx.doi.org/10.1109/isscc.2009.4977308 - 3. Stackhouse, B., Bhimji, S., Bostak, C., Bradley, D., Cherkauer, B., Desai, J., Francom, E., Gowan, M., Gronowski, P., Krueger, D., Morganti, C. and Troyer, S. (2009) A 65 nm 2-Billion Transistor Quad-Core Itanium Processor. IEEE Journal of Solid-State Circuits, 44, 18-31.
http://dx.doi.org/10.1109/JSSC.2008.2007150 - 4. Kurd, N., Mosalikanti, P., Neidengard, M., Douglas, J. and Kumar, R. (2009) Next Generation Intel? Core? Micro- Architecture (Nehalem) Clocking. IEEE Journal of Solid-State Circuits, 44, 1121-1129.
http://dx.doi.org/10.1109/JSSC.2009.2014023� - 5. Duarte, D., Hsu, S., Wong, K., Huang, M. and Taylor, G. (2010) Interpolated VCO Design for Low Bandwidth, Low Jitter, Self Biased PLL in 45 nm CMOS. Custom Integrated Circuits Conference, San Jose, 19-22 September 2010, 1-4.
http://dx.doi.org/10.1109/cicc.2010.5617473 - 6. Song, Y., Wang, Y., Jia, S. and Zhao, B.Y. (2008) A Novel Calibration Technique Applying to an Adaptive-Bandwidth PLL. International Conference on Solid State and Integrated Circuit Technology, Beijing, 20-23 October 2008, 1933- 1936.
http://dx.doi.org/10.1109/icsict.2008.4734971 - 7. Sai, A., Kobayashi, Y., Saigusa, S., Watanabe, O. and Itakura, T. (2012) A Digitally Stabilized Type-III PLL Using Ring VCO with 1.01 psrms Integrated Jitter in 65 nm CMOS. IEEE International Solid-State Circuits Conference Digest of Technical Papers, San Francisco, 19-23 February 2012, 248-249.
- 8. Sun, H. and Moon, U.-K. (2015) MDLL/PLL Dual-Path Clock Generator. IEEE 58th International Midwest Symposium on Circuits and Systems, Fort Collins, 2-5 August 2015, 1-4.
- 9. Ferriss, M., Plouchart, J.-O., Natarajan, A., Rylyakov, A., Parker, B., Tierno, J.A., Babakhani, A., Yaldiz, S., Valdes- Garcia, A., Sadhu, B. and Friedman, D.J. (2013) An Integral Path Self-Calibration Scheme for a Dual-Loop PLL. IEEE Journal of Solid-State Circuits, 48, 1-12.
http://dx.doi.org/10.1109/JSSC.2013.2239114 - 10. Nonis, R., Da Dalt, N., Palestri, P. and Selmi, L. (2005) Modelling, Design and Characterization of a New Low-Jitter Analog Dual Tuning LC-VCO PLL Architecture. IEEE Journal of Solid-State Circuits, 40, 790-804.
http://dx.doi.org/10.1109/JSSC.2005.848037 - 11. Van de Beek, R.C.H., Vaucher, C.S., Leenaerts, D.M.W., Klumperink, E.A.M. and Nauta, B. (2004) A 2.5-10-GHz Clock Multiplier Unit with 0.22-ps RMS Jitter in Standard 0.18-μm CMOS. IEEE Journal of Solid-State Circuits, 39, 1862-1872.
http://dx.doi.org/10.1109/JSSC.2004.835833 - 12. Thambidurai, C. and Krishnapura, N. (2010) Spur Reduction in Wideband PLLs by Random Positioning of Charge Pump Current Pulses. IEEE International Symposium on Circuits and Systems, Paris, 30 May-2 June 2010, 3397-3400.
http://dx.doi.org/10.1109/iscas.2010.5537876 - 13. Hajimiri, A., Limotyrakis, S. and Lee, T.H. (1999) Jitter and Phase Noise in Ring Oscillators. IEEE Journal of Solid- State Circuits, 34, 1303-1309.
http://dx.doi.org/10.1109/4.766813 - 14. Dhurga Devi, J. and Ramakrishna, P.V. (2011) Performance Improvement for Maneatis PLL for Microprocessor Clock. 7th International Conference on Ph.D Research in Microelectronics & Electronics, Trento, 3-7 July 2011, 209-212.