Circuits and Systems
Vol.06 No.11(2015), Article ID:61124,15 pages
10.4236/cs.2015.611024
Single CDBA Based Voltage Mode Bistable Multivibrator and Its Applications
Rishi Pal1, Rajeshwari Pandey2*, Neeta Pandey2, Ramesh Chandra Tiwari1
1Department of Physics, Mizoram University, Aizawl, India
2Department of Electronics and Communication Engineering, Delhi Technological University, Delhi, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 September 2015; accepted 13 November 2015; published 16 November 2015
ABSTRACT
In this paper, current differencing buffered amplifier (CDBA) based bistable multivibrators are introduced. Each presented circuit is constructed using single CDBA as the basic active building block and three resistors. Two applications namely an astable and a monostable multivibrator are also realized to demonstrate the usefulness of the proposed bistable multivibrators. The presented circuits are simulated using PSPICE from Cadence Orcad16.2 to verify their functionality. Simulation results agree well with the theoretical analysis.
Keywords:
Schmitt Trigger, Bistable Multivibrator, CDBA, Monostable Multivibrator

1. Introduction
Inherent wide bandwidth which is virtually independent of closed loop gain, greater linearity, and large dynamic range are the key performance features of current mode technique [1] . The CDBA is one such active element which inherits these advantages. In addition, it is free from parasitic capacitances [2] and hence is appropriate for high frequency operation. It provides further flexibility to the designers, enabling a variety of circuit designs, as it can operate in both current and voltage mode [3] .
Bistable multivibrator, commonly known as Schmitt trigger, finds extensive applications in the fields of communication systems, instrumentation measurement systems, and power conversion control circuits [4] . It is commonly employed in monostable multivibrator [4] - [7] , square wave generator [8] - [12] , pulse width modulator (PWM) [13] [14] , etc. Several implementations of the Schmitt triggers using different high-performance active building blocks have been proposed in open literature [15] - [19] . Conventional voltage-mode bistable multivibrators [15] employ an op-amp with a positive feedback. Current mode building blocks based voltage output bistable multivibrators are presented in [16] - [19] . Schmitt trigger based on two operational transconductance amplifiers (OTAs) and two resistors is presented in [16] wherein the output amplitude and threshold level can be independently/electronically tuned. Schmitt triggers based on current conveyors are presented in [17] [18] which use only single active element and their outputs are temperature-insensitive. Bistable multivibrator configurations using single operational transresistance amplifier (OTRA) are proposed in [19] which provide both Clockwise (CW) and counter clock wise (CCW) hysteresis functions. A compartaive statement of the existing voltage mode schmitt triggers is reported in Table 1.
It may be observed from the table that
- the op-amp based structures [15] though provide voltage output at appropriate impedance level yet the constant gain-bandwidth product and lower slew rate of the op-amps limit their high frequency operations.
- the structure proposed in [16] provides temperature sensitive output
- the configurations of [16] - [18] provide voltage output at high impedance and hence require a buffer to drive the voltage input circuits. This increases the component count in the circuit.
- the structures presented in [17] [18] provide only CW hysteresis
- the OTRA based structures [19] can be used both for voltage and current inputs, however output can be only voltage type
- the CDBA based structure provides further flexibility as it can be driven by both voltage and current inputs and can provide both voltage and current outputs
Above discussion suggests that CDBA based design is one of the most suitable choice. To the best of authors’ knowledge no CDBA based schmitt trigger circuit is available in literature. Thus this paper aims at introducing new CW and CCW Schmitt Triggers, using single CDBA and three resistors which will provide further flexibility to circuit designers. The PSPICE simulation results are also shown, which are in correspondence to the theoretical analysis. To show the usefulness of the presented circuits, the applications of the Schmitt triggers as square wave/triangular wave generator and monostable multivibrator are introduced.
The remaining paper is organized as follows. In Section 2 the function of a CDBA is introduced followed by the description of proposed circuits. The PSPICE simulations and experimental results to investigate the circuit performances are presented in Section 3 which are in confirmation with the theoretical propositions. In Section 4, application examples of the proposed circuits are given. The concluding remarks are presented in Section 5.
2. Circuit Description
The circuit symbol of CDBA is shown in Figure 1 and the port characteristics are given by Equation (1)
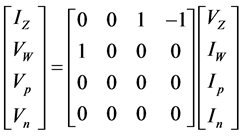 (1)
(1)
Table 1. Comparison of existing voltage mode schmitt triggers.
Figure 1. Block diagrammatic representation of CDBA.
2.1. The CW Schmitt Trigger
The proposed CW Schmitt Trigger configuration is shown in Figure 2(a). The Input is provided through a small resistance R1 at n terminal of the CDBA and output vo is taken across w terminal. A high value resistance RZ is connected at the z terminal of the CDBA which forces the circuit into saturation. Resistor R2 forms a positive feedback loop to the ‘p’ input of the CDBA. Thus, the CDBA output saturates either at +Vsat, the positive saturation level or at the negative saturation level ?Vsat. This circuit realizes the CW hysteresis characteristic as shown in Figure 2(b).
For the CW hysteresis operation, the output Vo is initially assumed to be at the positive saturation level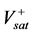 . The current Ip and In of CDBA are given by
. The current Ip and In of CDBA are given by
 (2)
(2)
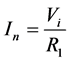 (3)
(3)
As Vi increases from zero, Vo remains at  until Vi reaches the upper threshold voltage VTH thereby changing the output level from
until Vi reaches the upper threshold voltage VTH thereby changing the output level from  to
to  . This output level is maintained as long as Vi is greater than the lower threshold voltage VTL. Assuming that Vo is at
. This output level is maintained as long as Vi is greater than the lower threshold voltage VTL. Assuming that Vo is at 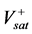 and Vi is smaller than VTH initially, Ip can be determined from Equation (3) as
and Vi is smaller than VTH initially, Ip can be determined from Equation (3) as
 (4)
(4)
As vi increases, current In gets closer to Ip and when In exceeds Ip, the output Vo switches to its negative saturation level  . From Equations (3) and (4), the upper threshold voltage VTH can be computed when Ip is equal to In and can be expressed as
. From Equations (3) and (4), the upper threshold voltage VTH can be computed when Ip is equal to In and can be expressed as
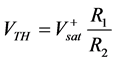 (5)
(5)
The current of p terminal can now be computed as
 (6)
(6)
However, In remains same as Equations (3). By equating Ip and In the lower threshold voltage VTL can be determined as
 (7)
(7)
The output level will switch back to 
2.2. The CCW Schmitt Trigger
The CCW Schmitt Trigger is shown in Figure 3(a) wherein, the input voltage is connected at p terminal of CDBA. The currents Ip and In can be computed as

Figure 2. (a) CW Schmitt Trigger; (b) CW Hysteresis Curve.

Figure 3. (a) CCW Schmitt Trigger; (b) CCW Hysteresis Curve.


Assuming that Vo is at 

When Vi is smaller than VTL, output Vo switches to 

Hysteresis Curve for CCW Schmitt Trigger is shown in Figure 3(b).
2.3. Schmitt Trigger with Reference Voltage
For the circuits shown in Figure 2(a) and Figure 3(a) the VTH = −VTL and hence the switching voltage (VST) defined as (VTH + VTL)/2 is zero. Some applications require that VTH and VTL both should either be positive or negative resulting in finite value of VST. This can be accomplished by adding a reference voltage to the circuit of Figure 2(a) and Figure 3(a) which results in following four configurations
1. CW Schmitt Trigger with positive VST, shown in Figure 4(a),
2. CW Schmitt Trigger with negative VST, depicted in Figure 4(b),
3. CCW Schmitt Trigger with positive VST, given in Figure 5(a),
4. CCW Schmitt Trigger with negative VST, shown in Figure 5(b).
For the circuit of Figure 4(a) Ip and In are given as


Using routine analysis the VTH and VTL can be computed as


where


Figure 4. (a) CW Schmitt Trigger with positive VST; (b) CW Schmitt Trigger with negative VST.


Figure 5. (a) CCW Schmitt Trigger with positive VST; (b) CCW Schmitt Trigger with negative VST.

Similarly the VTH and VTL for negative switching, as given in Figure 4(b), can be derived as


For CCW Schmitt Trigger with positive switching voltage, the threshold voltages VTH and VTL are given by Equations (14) and (15) respectively whereas for CCW configuration with negative switching voltage are given in Equations (17) and (18) respectively.
3. Simulation and Experimental Results
To validate the theoretical predictions, the proposed bistable multivibrator circuits have been simulated using PSPICE. The CDBA is realized using current feedback operational amplifier (CFOA) IC AD 844 as shown in Figure 6 [2] . PSPICE Macro model of CFOA IC AD 844AN [20] is used for simulations and supply voltages used are ±10 V.
Figure 7(a) shows the simulation results of CW Configuration for RZ = 500 kΩ, R1 = 5 kΩ, R2 = 10 kΩ. The
Figure 6. CFOA based implementation of CDBA [2] .


Figure 7. (a) Output of the CW Schmitt Trigger; (b) CW Hysteresis Curve.
saturation levels are ±6.3 V. The input voltage is a 50 Hz sinusoid with signal swing from −8 V to +8 V. The simulated threshold levels are ±3 V which are in accordance with the theoretically computed value of ±3.15 V. Figure 7(b) shows the hysteresis curve for CW configuration. The results for CCW configuration are depicted in Figure 8 wherein, the component values and supply voltages are chosen same as that for the CW operation.
The transient responses for CW and CCW configurations are shown in Figure 9(a) and Figure 9(b) respectively for an input frequency of 250 KHz.
The frequency response of CW Schmitt Trigger is shown in Figure 10 having 3 dB bandwidth as 2.6 MHz.
Transient response for CCW for positive switching voltage is shown in Figure 11(a) for VTH = 6 V and VTL = 2 V and corresponding transfer characteristics is shown in Figure 11(b). The component values are computed as RZ = 500 kΩ, R1 = 3.17 kΩ, RS = 4.6 kΩ, R2 = 10 kΩ and Vdc = 5 V. Transient response and hysteresis curve for CW configuration with negative switching voltage for VTH = 6 V and VTL = 2 V are shwon in Figure 12(a) and Figure 12(b) respectively. The simulated results are in close agreement with theoretical values for both the configurations.


Figure 8. (a) Output of the CCW Schmitt Trigger; (b) CCW Hysteresis Curve.


Figure 9. Outputs for 250 KHz input signal (a) CW output; (b) CCW output.
Figure 10. Frequency response of CW Schmitt Trigger.


Figure 11. (a) CCW output with positive switching voltage; (b) CCW Hysteresis Curve with positive switching voltage.
Figure 13(a) shows the experimental results of CW Configuration for RZ = 100 kΩ, R1 = 4.7 kΩ, R2 = 4.7 kΩ with supply voltage of ±12 V. The saturation levels are ±10 V. The input voltage is a 1 KHz sinusoid with signal swing from −10 V to +10 V. The observed threshold levels are ±10 V which are same as the theoretically computed value. Figure 13(b) shows the hysteresis curve for CW configuration and the experimental output for CCW configuration for an applied input voltage of 6 KHz sinusoid with signal swing from −10 V to +10 V is presented in Figure 13(c). The component values are chosen as RZ = 100 kΩ, R1 = 4.7 kΩ, R2 = 4.7 kΩ and supply voltages are ±8 V. Observed saturation voltages are ±6 V giving threshold voltages as ±6 V and are equal to theoretical values.
4. Applications
In the following subsections two well known applications of Schmitt trigger namely triangular/square wave Generator and monostable multivibrators are developed to demonstarte the utility of proposed work in circuit applications.


Figure 12. (a) CW output with negative switching voltage; (b) CW hy- steresis curve with negative switching voltage.

Figure 13. Experimental results (a) output of CW Schmitt Trigger; (b) hysteresis curve for CW configuration; (c) output of CCW Schmitt Trigger.
4.1. Triangular/Square Wave Generator
The circuit of CDBA Schimitt trigger based triangular/square wave generator is shown in Figure 14. The circuit can be viewed as two cascaded blocks. The circuitry comprising of CDBA I is a Schmitt trigger, while the cir-
Figure 14. Triangular/square wave generator.
cuit comprising of CDBA II, is a simple integrator. The Schmitt trigger continuously compares the current Ip1 and In1 and accordingly the output Vo1 swings repetitively between positive saturation level 







This gives frequency of oscillation as

The simulated square wave output Vo1 and triangular output Vo2 are shown in Figure 15 for R1 = 10 kΩ, R2 = 100 Ω, R3 = 20 kΩ, R4 = 5 kΩ, and C = 1 µF.
4.2. Monostable Multivibrator
The realization of the monostable multivibrator is shown in Figure 16. The positive feedback loop is completed using the capacitor and a resistor. Under stable state the Vc is clamped by diode. To ensure the stable-state operation, RZ must be high enough to make output voltage Vo switch to positive saturation level


Now if a positive-edge triggering signal Itrig is applied at terminal n of CDBA, the circuits enter into the quasi- stable State. As In is more positive than Ip the output voltage Vo jumps to 


And capacitor discharging equation can be expressed as

Figure 15. Output of triangular/square wave generator.
Figure 16. Monostable multivibrator.
at t = T2 the capacitorvoltage reaches the threshold voltage VTL, when output voltage switches back to

From Equations (25) and (26) the pulse width T (T2 − T1) for which the circuit remains in quasi stable sate can be computed as

Figure 17 shows the output of monostable multivibrator for RF = 20 kΩ, RZ = 500 kΩ, C = 10 nF having T = 59 µs as against calculated value of 64 µs.
Figure 17. Output of monostable multivibrator.
5. Conclusion
In this paper single CDBA based bistable multivibrator configurations are proposed which include CW, CCW Schmitt Triggers with and without reference voltage. Two applications namely square wave/triangular wave generator and monostable multivibrator are realized to demonstrate the usefulness of the proposed bistable multivibrators. The simulation and experimental results are found to be in close agreement to theoretical predictions. The proposed configurations are one of the best choices for voltage mode applications. Also, due to inherent flexibility of signal usage in CDBA the proposed configurations can easily be extented to current/transimped- ance/transadmittance mode depending upon the applications.
Cite this paper
Rishi Pal,Rajeshwari Pandey,Neeta Pandey,Ramesh Chandra Tiwari, (2015) Single CDBA Based Voltage Mode Bistable Multivibrator and Its Applications. Circuits and Systems,06,237-251. doi: 10.4236/cs.2015.611024
References
- 1. Toumazou, C., Lidgey, F.J. and Haigh, D.G. (1990) Analogue IC Design: The Current Mode Approach. Peter Peregrinus Ltd., London.
- 2. Acar, C. and Ozuguz, S. (1999) A New Versatile Building Block: Current Differencing Buffered Amplifier Suitable for Analog Signal Processing Filters. Microelectronics Journal, 30, 157-160.
http://dx.doi.org/10.1016/S0026-2692(98)00102-5 - 3. Cakir, C. and Cicekoglu, O. (2008) Low-Voltage High-Performance CMOS Current Differencing Buffered Amplifier (CDBA). Proceedings of IEEE PRIME Conference, Istanbul, 22 June 2008-25 April 2008, 37-40.
http://dx.doi.org/10.1109/rme.2008.4595719 - 4. Chien, H.-C. and Lo, Y.-K. (2011) Design and Implementation of Monostable Multivibrators Employing Differential Voltage Current Conveyors. Microelectronics Journal, 42, 1107-1115.
http://dx.doi.org/10.1016/j.mejo.2011.07.005 - 5. Chung, W.-S., Cha, H.-W. and Kim H.-J. (2002) Current-Controllable Monostable Multivibrator Using OTAs. IEEE Transactions on Circuits and Systems I, 49, 703-705.
http://dx.doi.org/10.1109/TCSI.2002.1001963 - 6. Lo, Y.-K. and Chien, H.-C. (2006) Current-Mode Monostable Multivibrators Using OTRAs. IEEE Transactions on Circuits and Systems II: Express Briefs, 53, 1274-1278.
http://dx.doi.org/10.1109/TCSII.2006.882361 - 7. Lo, Y.-K. and Chien, H.-C. (2007) Single OTRA-Based Current Mode Monostable Multivibrator with Two Triggering Modes and a Reduced Recovery Time. IET Circuits, Devices & Systems, 1, 257-261.
http://dx.doi.org/10.1049/iet-cds:20060359 - 8. Almashary, B. and Alhokail, H. (2000) Current-Mode Triangular Wave Generator Using CCIIs. Microelectronics Journal, 31, 239-243.
http://dx.doi.org/10.1016/S0026-2692(99)00106-8 - 9. Siripruchyanun, M. and Wardkein, P. (2001) Temperature Insensitive and Electronically Adjustable Square/Triangular Wave Generation Based on Novel Schmitt trigger Oscillator. Proceedings of ISIC2001 9th International Symposium on Integrated Circuits, Devices and Systems, 219-222.
- 10. Hung, W.-S., Kim, H., Cha, H.-W. and Kim, H.-J. (2005) Triangular/Square-Wave Generator with Independently Controllable Frequency and Amplitude. IEEE Transactions on Instrumentation and Measurement, 54, 105-109.
http://dx.doi.org/10.1109/TIM.2004.840238 - 11. Haque, A.S., Hossain, M.M., Davis, W.A., Russell, H.T. and Carter, R.L. (2008) Design of Sinusoidal, Triangular, and Square Wave Generator Using Current Feedback Operational Amplifier (CFOA). 2008 IEEE Region 5 Conference, Kansas City, 17-20 April 2008, 1-5.
http://dx.doi.org/10.1109/tpsd.2008.4562735 - 12. Pal, D., Srinivasulu, A., Demonsthenous, A., Pal, B.B. and Das, B.N. (2009) Current Conveyor-Based Square/Triangular Waveform Generators with Improved Linearity. IEEE Transactions on Instrumentation and Measurement, 58, 2174-2180.
http://dx.doi.org/10.1109/TIM.2008.2006729 - 13. Siripruchyannun, M. and Wardkein, P. (2003) A Fully Independently Adjustable, Integrable Simple Current Controlled Oscillator and Derivative PWM Signal Generator. The IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E86-A, 3119-3126.
- 14. Kim, H., Kim, H.J. and Chung, W.S. (2007) Pulsewidth Modulation Circuits Using CMOS OTAs. IEEE Transactions on Circuits and Systems I: Regular Papers, 54, 1869-1878.
http://dx.doi.org/10.1109/TCSI.2007.904677 - 15. Sedra, A.S. and Smith, K.C. (2004) Microelectronic Circuits. 4th Edition, Oxford University Press, New York.
- 16. Kim, K., Cha, H.W. and Chung, W.S. (1997) OTA-R Schmitt Trigger with Independently Controllable Threshold and Output Voltage Levels. Electronics Letters, 33, 1103-1105.
http://dx.doi.org/10.1049/el:19970786 - 17. Diutaldo, G., Palumbo, G. and Pennisi, S. (1995) A Schmitt Trigger by Means of a CCII+. International Journal of Circuit Theory and Applications, 23, 161-165.
http://dx.doi.org/10.1002/cta.4490230207 - 18. Del, S.R., Marcellis, A.D., Ferri, G. and Stornelli, V. (2007) Low Voltage Integrated Astable Multivibrator Based on a Single CCII. Proceedings of 2007 PhD Research in Microelectronics and Electronics Conference, Bordeaux, 2-5 July 2007, 177-180.
- 19. Lo, Y.K., Chien, H.C. and Chiu, H.J. (2008) Switch-Controllable OTRA-Based Bistable Multivibrators. IET Circuits, Devices & Systems, 2, 373-382.
http://dx.doi.org/10.1049/iet-cds:20080011 - 20. Macromodel of AD 844 in PSPICE library.
http://espice.ugr.es/espice/src/modelos_subckt/Anal%C3%B3gicos/ad844.cir
NOTES
*Corresponding author.














