Circuits and Systems
Vol.06 No.10(2015), Article ID:60458,11 pages
10.4236/cs.2015.610021
Computer Platform Adaptive Interference Cancellation Using Higher-Order Statistics
Qiwei Wang1, Mario E. Magaña1, Harry G. Skinner2
1School of EECS, Oregon State University, Corvallis, OR, USA
2Intel Corporation, Hillsboro, OR, USA
Email: wangqi@onid.orst.edu, magana@eecs.oregonstate.edu, harry.g.skinner@intel.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 August 2015; accepted 19 October 2015; published 22 October 2015
ABSTRACT
Broadband wireless interference in a computer platform is the result of multiple dynamic electromagnetic emission sources. This interference is non-Gaussian and a receiver design based on the Gaussian assumption will yield suboptimal performance. In fact, it has a double-sided K-dis- tribution and needs to be treated differently in the design process. When dealing with this type of interference in the presence of white Gaussian noise, traditional interference/noise cancellation schemes do not produce satisfactory results. In this paper, we present an interference mitigation method which improves BER performance. We do this by using the cross-cumulant as the criterion of goodness. Specifically, our algorithm is based on higher order statistics (HOS) and is designed to reconstruct and to cancel the interference in a recursive fashion. The algorithm is tested on both BPSK and OFDM communication environments. We compare performance in terms of BER against other cancellation methods.
Keywords:
Broadband, Interference, Cancellation, Adaptive, Cumulant

1. Introduction
Electronic devices with wireless connection are more and more widely used in people’s daily life. Advanced wireless standards like 802.11b/g/n or 4G LTE are making all kinds of devices communicate at speeds of hundreds of megabits per second [1] [2] . However, noise and interference always prevent a system from achieving optimum performance. The Federal Communications Commission (FCC) has set a series of standards to limit the emission power of personal digital devices in order to prevent significant interference and human health issues [3] . According to FCC’s regulation, the radio circuit cannot be protected from the interference which is emitted by the device itself. This paper tries to solve this problem by finding an algorithm that cancels the interference emitted inside a computer platform. By computer platform we mean a platform with all components that may appear in an electronic computation device like a laptop or tablet, which include crystal clocks, CPUs, RAM, hard drive, interconnect ports and so on. The electromagnetic emission produced by these internal components becomes the self interference of the wireless transmitter/receiver which is an integral part of the same platform.
All these interfering signals can be classified into 2 categories: narrowband noise and broadband noise. The frequency spectrum of narrowband noise lies within the frequency span of the signal of interest, and the noise often appears as that whose peak amplitude is much greater than the signal of interest. Narrowband noise is generated by clocks of a certain frequency. Broadband noise, however, is the combination of several electromagnetic emissions, with a bandwidth that is wider than the antenna receiving bandwidth [4] . Figure 1 [5] shows the power spectrum of the platform self interference measured in the laboratory. To make these measurements, the platform is placed inside a special enclosure to shield it from external interfering signals.
This interference is modeled as a random noise signal with double-sided K-distribution [6] . In this paper, we propose a technique which can be applied in the receiver to cancel the interference signal. This approach can be cost-effective and easy to implement in a mobile computer platform.
To mitigate the effects of interference, designers first estimate the interference and then subtract the estimated interference signal from the actual received signal. Here we devise broadband interference mitigation algorithms for both BPSK and OFDM systems in the presence of both Gaussian noise and K-distributed interference. Alban [5] presented several estimation and mitigation methods for this particular case. For the narrow band case, a Normalized Linear Mean Square (NLMS) adaptive filter can be used to predict and cancel the interference signal and it is proved to be efficient. For the broadband case, several parameter estimation methods have been used and a method using an extended Kalman filter is presented in [5] , but the results are not satisfactory.
Specifically, our proposed method uses an adaptive filter that is based on higher-order statistics to reduce the K-distributed self interference observed in a computer platform. A similar adaptive algorithm which uses higher order statistics is first applied to broadband interference by Shin and Nikias [7] . Instead of using a criterion of goodness based on second-order statistics as most adaptive algorithms do (LMS, NLMS, Leaky LMS and so on), this algorithm uses a higher order statistics, i.e. the cumulant, to eliminate the effect of the co-existing Gaussian noise. The fourth-order statistics (FOS) adaptive canceller can be implemented in an OFDM receiver by assuming that a reference signal is available. Using computer simulation we show that this canceller is effective with or without the presence of Gaussian noise. Even though the BER performance is not as good at low SNR, the FOS canceller outperforms the extended Kalman filter and other estimators [5] by achieving a lower BER at medium to high SNR.
Figure 1. Computer platform noise.
The paper is organized as follows: in part II, we describe the problem. In Part III, we briefly describe the concept of cumulant and the structure of a high order cumulant adaptive algorithm. In section IV, the designs of the FOS canceller and implementation for both BPSK and OFDM-based platforms are presented. Interference canceller performance is verified via the computer simulation. Finally, in Section V, we present the conclusion of our work and propose lines of research which could improve performance using variants of the FOS-based canceller.
2. Problem Description
Figure 2 illustrates the scheme of this interference cancellation problem. The primary received wireless signalcan be expressed as
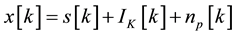 , (1)
, (1)
where  is the signal of interest (SOI).
is the signal of interest (SOI). 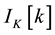 is the double-sided K-distributed interference with the probability density function [8]
is the double-sided K-distributed interference with the probability density function [8]
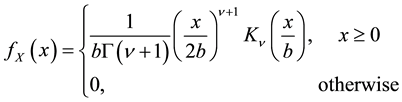 , (2)
, (2)
where b is a positive scalar, v is the shape parameter that satisfies the condition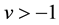 ,
, 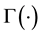 is the Gamma
is the Gamma
function, and 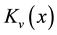 is the modified Bessel function of order v described by
is the modified Bessel function of order v described by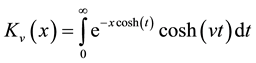 .
.
 is Gaussian distributed noise whose average power is less than that of
is Gaussian distributed noise whose average power is less than that of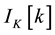 .
.
The reference input signal is described by
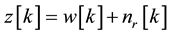 , (3)
, (3)
where 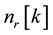 is Gaussian distributed noise that is independent of
is Gaussian distributed noise that is independent of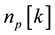 .
. 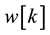 and the interference signal
and the interference signal 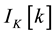 are related to each other as follows:
are related to each other as follows:

In other words, 

Figure 2. Cancellation scheme.
transfer function




Our goal is to find an algorithm using 



3. Higher Order Statistics (HOS) Algorithm
3.1. Cumulants
The high order statistics used in this algorithm are the cumulants. Given a set of n real-valued random variables

where 

We can express the cumulants in terms of the moments [9] . Now, if




It is pointed out in [10] that the third and higher order cumulants of a Gaussian process are zero. That is one of the reasons why cumulants are chosen to be the “criterion of goodness” in an algorithm mitigating non- Gaussian interference in the presence of Gaussian noise.
3.2. HOS Algorithm
Because the n-th order cumulant of any Gaussian process is identically zero for

Let 



in which the cumulant operator is defined as [9]

i.e. a special case of Equation (6) that
Let 




Comparing (11) and (12) leads to the conclusion that if






while 



Finally, it can be shown that

Thus, the “criterion of goodness” is finally defined as

where P is a subset of the 
In matrix form,

To obtain the optimum filter coefficients, we minimize 


If we denote the number of points in set P as M and N as the number of taps of the FIR filter








The filter coefficients are updated recursively by

The value of the step size m depends on the order of the algorithm and the behavior of the noise signal. The strategy to find an appropriate value of m will be discussed later under the condition that a FOS algorithm is applied on K-distributed interference. Figure 3 shows the structure of the proposed HOS interference canceller.
4. FOS Canceller and OFDM Implementation
4.1. Fourth-Order Statistics (FOS) Algorithm
Since the fourth order statistic is used, we only need a domain such that
Figure 3. HOS interference canceller structure.
Shin and Nikias [7] provided the following domain selection when cancelling a sinusoidal interference with uniformly distributed random phase:
Note that the number of points M satisfies

Assuming the input process is ergodic, we can compute an estimate of the fourth-order cumulant as follows:


The step-size parameter applied to the FOS cancelleris [7]

in which 
Now, a small step-size may result in long convergence time when the SIR is large, while a large step-size may not permit the algorithm to converge when the SIR is low and a variable step-size scheme may be needed. The details of the adaptive scheme will be given shortly.
4.2. OFDM Implementation
Although the FOS interference canceller works fairly well when the interference is K-distributed, it still needs some modification to work properly in an OFDM communication environment. First, the received OFDM- modulated signal is complex but the FOS canceller only works on real-valued signals. Second, similar to the NMLS algorithm, we need to normalize the input signal to make sure the algorithm will converge. The time domain cancellation scheme is depicted in Figure 4.
If the received signal is denoted as

where 
5. Simulation Results
The simulation results are all based on Gaussian wireless channel. To evaluate the best performance of the higher-order static algorithm, the channel is considered free from any fading effect.
5.1. BPSK Receiver Case
We first evaluate performance of the proposed algorithm design in a platform that uses a binary phase shift keyed (BPSK) digital communication system. The signal of interest used in the BPSK-based platform is obviously different than that used in a computer platform that uses OFDM communications in their transceivers.
The simulation parameters are listed in Table 1.
The variable step-size parameter is set to

From Figures 5-8, we can clearly see on a qualitative basis that the canceller works well for SIRs of 5 dB and 12.5 dB. Quantitatively, after cancellation, the power of the K-distributed interference is reduced by 36% and 32% at 5 and 12.5 dB, respectively. The cancellation algorithm converges before the first 2000 samples, which takes microseconds in most modern wireless communication systems implemented in computer platforms. The BER improvement after interference cancellation can be observed in Figure 9. This figure shows 5 simulation results, namely, one before cancellation and four after cancellation, in the SIR range from 0 dB to 15 dB. The improvement can be as large as 6 dB at SIR of 5 dB. Hence, we can conclude that the FOS-canceller with variable step- size works well in a computer platform that uses BPSK communications in the presence of K-distributed interference.
5.2. OFDM Receiver Case
Table 2 lists the parameters used in the OFDM modulation simulation environment. The composition of each frame during the ODFM modulation is now described. After the serial to parallel conversion, the pilot symbols are inserted evenly throughout the frame. If the n-th pilot symbol is denoted as Pn and the n-th QAM modulated symbol is denoted as Xn, the frame is described by
Figure 4. FOS canceller for an OFDM receiver.
Table 1. Binary simulation parameters.
Figure 5. Interference before canceller for SIR = 5 dB.
Figure 6. Interference after canceller for SIR = 5 dB.
Figure 7. Interference before canceller for SIR = 12.5 dB.
Figure 8. Interference after canceller for SIR = 12.5 dB.
Figure 9. BPSK receiver BER performance in the presence of K-distributed interference.
Table 2. OFDM simulation parameters.
Note that in an actual OFDM modulator, the location of pilot symbol should not be the same for each frame. However, since the locations of pilot symbols have nothing to do with the cancellation algorithm in this problem, the pilot symbols are set at fixed locations in each frame.
The IFFT is performed right after the pilot symbol insertion. The IFFT size applied here is 1024 and it is greater than the actual number of symbols in a single frame, i.e. 840. Zeros are added at the beginning and the end of each frame to make each frame contains exactly 1024 symbols, as follows:

After the IFFT of length 1024, the frame is described by

Finally, the prefix symbols are added and the OFDM modulated frame is described by

a) Performance evaluation for fixed K-distribution parameter
The first scenario we consider to evaluate OFDM system performance uses a K-distribution with a fixed set of parameters, namely,



System performance is shown in Figure 10. We can see that the FOS canceller results in consistent BER improvement for all SIR values. Also, at low SIR (2.5 dB) the improvement is better than traditional cancellation schemes.
b) Performance evaluation for different K-distribution parameters
Alban [6] pointed out that a change in the K-distribution parameters may result in different BER performances for the same cancellation algorithm. In case a) 

It is clear from this figure that the shape parameters b and v do affect system performance. The larger the b, the wider the probability density function of the interference. Regardless of their values, the interference cancellation strategy herein proposed consistently results in performance improvement. We can also see from the figure that case a) outperforms case b). This difference is not as high as that achieved in [6] , however, the BER performance is much better than the result in [6] at low SIR values. When SIR = 2.5, FOS canceller and the discrete Kalman filter both can produce a BER between 0.1 and 0.01. But when SIR = 10, the BER produced by
Figure 10. OFDM receiver BER performance with fixed K-distribution parameters.
Figure 11. BER performance in an OFDM receiver with different K- distributed parameter.
our proposed FOS canceller is around 10−4 while the result of discrete Kalman filter is in the neighborhood of 0.01. This improvement is at the cost of computational complexity and the additional requirement of knowing the reference signal.
6. Conclusion
This paper applied a new noise/interference cancellation algorithm to a computer platform interference cancellation problem. Based on previous research, this new algorithm focused on the cancellation of the broadband K-distributed interference. Higher order cumulants were introduced as the new criterion of goodness. The new algorithm used the higher order cumulants to improve the filter coefficients and reconstructs the interference signal from the reference signal. We verified through simulation that the fourth order statistics (FOS) algorithm was capable of mitigating the effect of K-distributed interference. A variable step-size mechanism was also introduced to ensure the convergence of the algorithm. Furthermore, the FOS algorithm was implemented in an ODFM system and its performance was compared to that of the discrete Kalman filter. The BER performance of FOS canceller was better than the previous method.
Cite this paper
QiweiWang,Mario E.Magaña,Harry G.Skinner, (2015) Computer Platform Adaptive Interference Cancellation Using Higher-Order Statistics. Circuits and Systems,06,201-212. doi: 10.4236/cs.2015.610021
References
- 1. Parkvall, S. and Astely, D. (2009) The Evolution of LTE towards IMT-Advanced. Journal of Communications, 4, 146-154.
http://dx.doi.org/10.4304/jcm.4.3.146-154 - 2. (2011) IEEE Standard for Information Technology—Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 8: IEEE 802.11 Wireless Network Management. IEEE Std. 802.11v-2011, New York, 9 February 2011, 1-433.
- 3. Federal Communications Commission (2012) Radiated Emission Limits. Code of Federal Regulations, 109, 800.
- 4. Alban, E.X., Magana, M.E., Skinner, H.G. and Slattery, K.P. (2012) Statistical Modeling of the Interference Noise Generated by Computing Platforms. IEEE Transactions on Electromagnetic Compatibility, 54, 574-584.
- 5. Alban, E.X. (2011) Immune Radio Architecture for Platform Interference. PhD Thesis, Oregon State University, Corvallis.
- 6. Kay, S. (2010) Representation and Generation of Non-Gaussian Wide-Sense Stationary Random Processes with Arbitrary PSDs and a Class of PDFs. IEEE Transactions on Signal Processing, 58, 3448-3458.
- 7. Shin, D.C. and Nikias, C.L. (1994) Adaptive Interference Canceler for Narrowband and Wideband Interferences Using Higher Order Statistics. IEEE Transactions on Signal Processing, 42, 2715-2728.
http://dx.doi.org/10.1109/78.324737 - 8. Iskander, D.R. and Zoubir, A.M. (1999) Estimation of the Parameters of the K-Distribution Using Higher Order and Fractional Moments. Transactions on Aerospace and Electronic Systems, 35, 1453-1457.
http://dx.doi.org/10.1109/7.805463 - 9. Nikias, C.L. and Petropulu, A.P. (1993) Higher-Order Spectra Analysis: A Nonlinear Signal Processing Framework. PTR Prentice Hall, Inglewood Cliffs.
- 10. Nikias, C.L. and Raghuveer, M.R. (1987) Bispectrum Estimation: A Digital Signal Processing Framework. Proceedings of the IEEE, 75, 869-891.
http://dx.doi.org/10.1109/PROC.1987.13824













