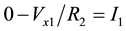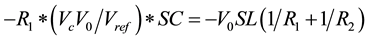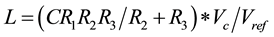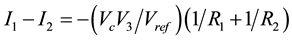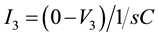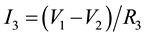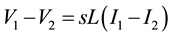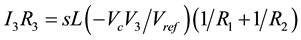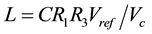Circuits and Systems
Vol.06 No.09(2015), Article ID:60006,10 pages
10.4236/cs.2015.69020
A Configuration for Realizing Voltage Controlled Floating Inductance and Its Application
Praween K. Sinha, Dr Neelam Sharma, Rohit Mishra
Electronics and Communication Department, Maharaja Agrasen Institute of Technology, New Delhi, India
Email: praweenrsinha@rediffmail.com, neelam_sr@yahoo.com, rtmishra92@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 June 2015; accepted 25 September 2015; published 28 September 2015
ABSTRACT
A configuration using current feedback amplifiers AD844 and multiplier AD534 has been presented, which is capable of realizing Voltage Controlled Floating Inductance (proportional and inverse proportional). The application of band pass filter in Figure 4(a), notch filter in Figure 5(a) and Hartley oscillator in Figure 6(a) and simulation result in Figures 4(b)-(d), Figures 5(b)-(d), Figures 6(b)-(d) shows the workability of proposed configuration.
Keywords:
Inductance Simulation, Voltage-Controlled Impedances, Multiplier, Filter, Oscillator, Current Feedback Operational Amplifier

1. Introduction
Simulation of inductor has been popular area of analog circuit research. Due to the well known difficulties of realizing on chip inductors of moderate to high values and high quality factors, simulated inductors have been the alternative choice for realizing inductor-based integrated circuit. Simulated inductors are also useful in discrete designs in which case they can replace bulky Passive inductors and after the advantages of reduced size, reduced cost and complete elimination of undesirable mutual coupling when several inductors are being used in a circuit.
Electronically controlled inductor such as voltage controlled floating inductance finds application in automatic gain controller, filter and oscillator circuit. A number of configuration using a variety of active elements such as op-amps, operational-mirrored amplifier, current controlled conveyors, OTA and Combination have so far been presented in the literature for realizing such elements in Floating Form [1] -[16] .
Recently, the current feedback op-amps (CFOAs) such as AD844 have attracted considerable attention in literature as alternative building blocks for analog circuit design due to the following advantages
i) Widen bandwidth that is relatively independent closed loop gain.
ii) Very high slew rate (2000 V/us).
iii) Ease of realizing various functions with least number of external passive components.
The main objective of paper is therefore to present a new configuration which is capable of realizing voltage controlled Floating inductance both in proportional and inversely proportional form and its application.
The paper is organized as follow:
Figure 1(a) is the basic terminal equation of CFOA.
Figure 1(b) is the basic structure of multiplier.
Figure 2(a) is the first case of the floating voltage controlled inductance.
Figure 3(a) is the another case of floating voltage controlled inductance
Figure 4(a) explained the application of voltage controlled inductance as BPF.
Figure 5(a) explained the application of voltage controlled inductance as notch filter.
Figure 6(a) explained the application of voltage controlled inductance as an oscillator.
Terminal Equations of CFA:
・
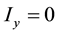
・

・
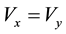
・
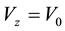
As shown in Figure 1(a). The x and y terminal of CFA are denoted by (−) sign and (+) sign respectively. A CFA is equivalent to a plus type conveyor with a voltage buffer and is very suitable building block for realization of active circuit.
MPY534 as MULTIPLIER
Description
The MPY534 is a highly accurate, general purpose four-quadrant analog multiplier. Its accurately laser trimmed transfer characteristics make it easy to use in a wide variety of applications with a minimum of external parts and trimming circuitry. Its differential X, Y and Z inputs allow configuration as multiplier, squarer, divider, square-rooter and other functions while maintaining high accuracy.
2. Proposed Configuration
2.1. Case 1
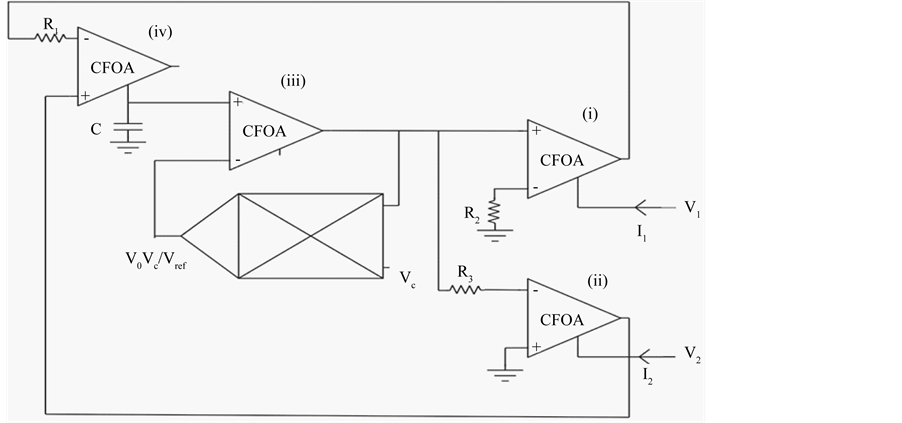
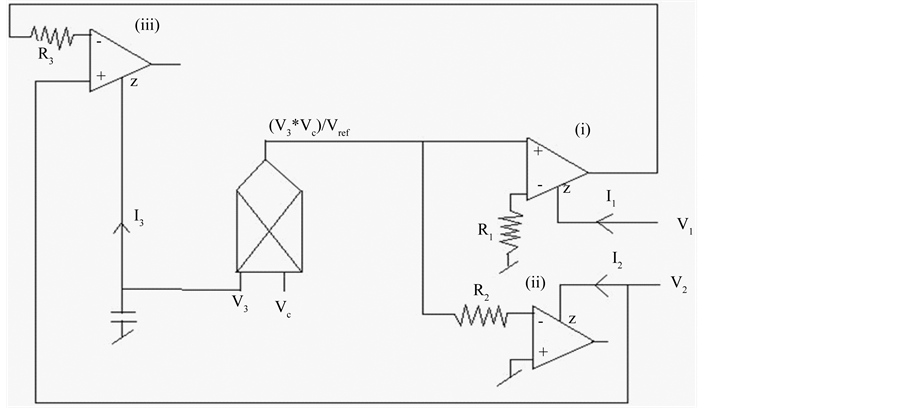
Implementation of voltage controlled floating inductance which is directly proportional to control voltage (Vc).
The proposed configuration shown in the Figure 2(a) where each CFOAs is characterized by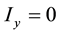 ,
,
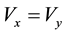 ,
,
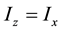 ,
,
 and multiplier with two resistance and capacitance is used for realizing the voltage controlled floating inductance.
and multiplier with two resistance and capacitance is used for realizing the voltage controlled floating inductance.
Mathematical Analysis
From CFOA (3) applying KCL
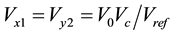 (1)
(1)
From CFOA (4) Applying KCL across capacitor:
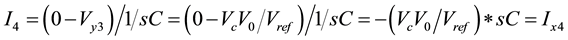 (2)
(2)
Applying KCL again at input port of CFOA (4)
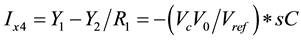
Thus
 (3)
(3)
From CFOA (2)
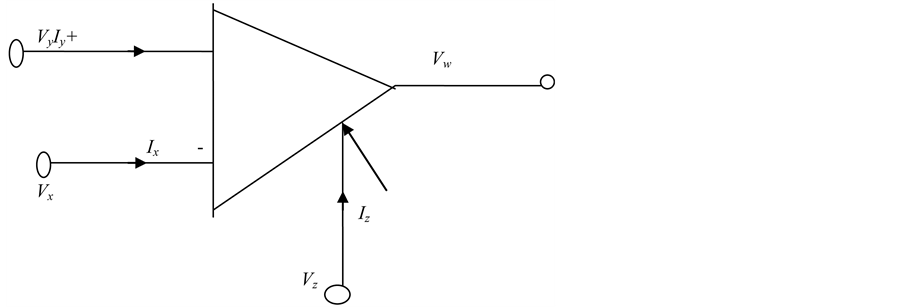

Figure 1. (a) CFA Symbol; (b) Multiplier pin diagram.
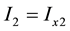
Applying KCL
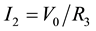 (4)
(4)
From CFOA(1)
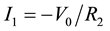
Now subtracting the equation no. (5) from equation No. (4)
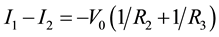
Now from standard floating inductor:
Putting the value of (V1 − V2) and (I1 − I2) from Equation (3) and (6)
After simplification we get,

Figure 2. (a) Proposed floating voltage controlled inductance configuration; (b) Realized floating inductor.
Thus inductance (L) is directly proportional to control voltage (Vc)
2.2. Case 2
Implementation of voltage controlled floating impedance with inversely proportional to control voltage.
The proposed configuration shown in the Figure 3(a). where each CFOAs is characterized by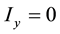



Mathematical Analysis
Output of the multiplier
From CFOA (1)
Applying KCL across capacitor

Now from CFOA (2)

Now subtracting the equation No. (1) from equation No. (2)
From CFOA (3) Applying KCL across capacitor we get
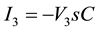
Again applying KCL at input node

Figure 3. (a) Proposed floating linear voltage controlled inductance configuration; (b) Realized floating inductor.
rearranging the equation we get,

Now from standard floating inductor:
Putting the value of (V1 − V2) and (I1 − I2) from Equation (3) and (4)
Putting the value of I3
After simplifying we get,
Thus inductance (L) is inversely proportional to control voltage (Vc)

Thus inductance is inversely proportional to control voltage (Vc).
3. Application of Floating Inductor Realized in Figure 2(a) and Figure 3(a)
3.1. Band Pass Filter
In Figure 4(a), we realized a Band pass filter using voltage controlled floating inductance and resistance, capacitance.
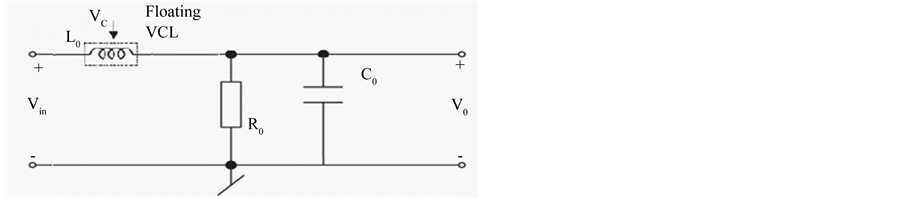
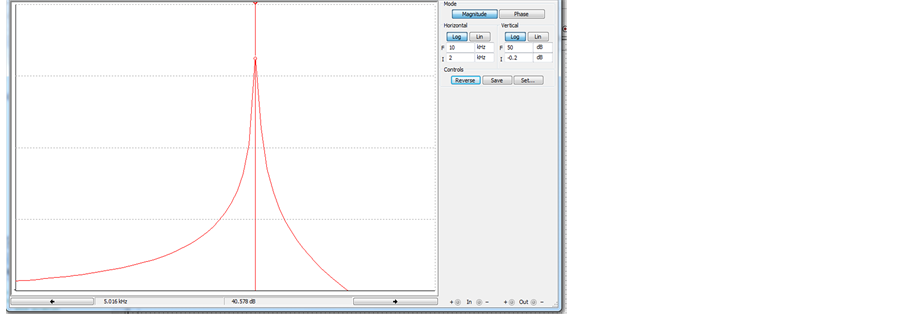

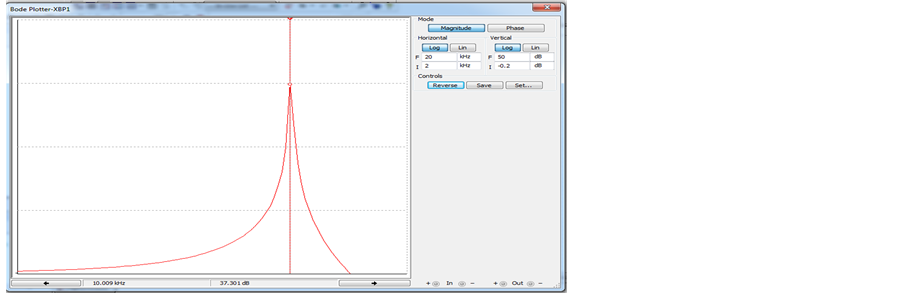
Figure 4. (a) A passive prototype RLC band pass filter; (b) Frequency response of the band pass filter (with C0 = 10 uF, R0 = 1 K, Vc = 1 V, L0 = 0.1 mH); (c) Frequency response of the band pass filter (with C0 = 10 uF, R0 = 1 K, Vc = 2 V, L0 = 0.05 mH); (d) Frequency response of the band pass filter (with C0 = 10 uF, R0 = 1 K, Vc = 4 V, L0 = 0.025 mH).
3.1.1. Simulation Results
Please see Figures 4(b)-(d).
3.1.2. Result
In the above simulation result, we show the frequency response of band pass filter made from voltage controlled floating inductance, a resistance and a capacitor. The band pass filter was designed for frequency f0 = 5 kHz, 7.1 kHz and 10 kHz with different value of inductance as given in Table 1. The center frequency of filter was found to be electronically tunable from 5 kHz to 10 kHz with Vc varying from 1 to 4.
Thus from the above result it can be seen that by varying the control voltage (Vc) center frequency (Fc) of the band pass filter can be changed . Thus we can control the center frequency by varying Vc.
3.2. Notch Filter
In Figure 5(a), we realized a RLC notch filter using voltage controlled floating inductance and resistance, capacitance.
3.2.1. Simulation Results
Please see Figures 5(b)-(d).
3.2.2. Result
In the above simulation result, we show the frequency response of notch filter made from voltage controlled floating inductance, a resistance and a capacitor. The notch filter was designed for frequency f0 = 5 kHz, 7.1 kHz and 10 kHz with different value of inductance as given in Table 2. The center frequency of filter was found to be electronically tunable from 5 kHz to 10 kHz with Vc varying from 1 to 4.
Thus from the above result it can be seen that by varying the control voltage (Vc) center frequency (Fc) of the notch pass filter can be changed .Thus we can control the center frequency by varying Vc.
3.3. Hartley Oscillator
In Figure 6(a), we realized an op-amp Hartley oscillator using voltage controlled floating inductance and, capacitance.
3.3.1. Simulation Results
Please see Figures 6(b)-(d).
3.3.2. Result
In the above simulation results, we show the frequency response of Hartley oscillator made from voltage controlled
Table 1. Effect of variation in control voltage (Vc) on center frequency (fc) of band pass filter.
Table 2. Effect of variation in control voltage (Vc ) on center frequency (fc) of notch filter.


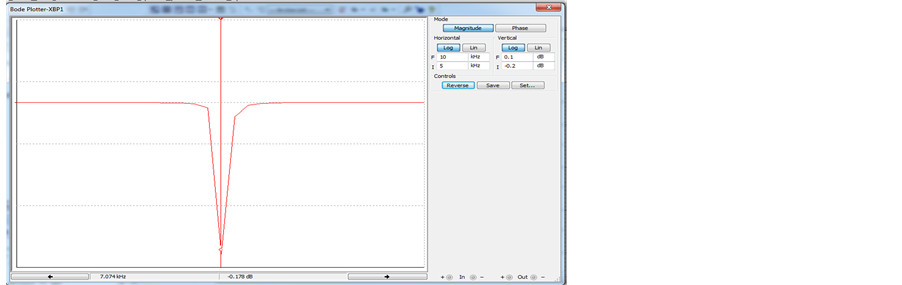

Figure 5. (a) A passive prototype RLC notch filter; (b) Frequency response of the notch filter (with C0 = 10 uF, R0 = 1 K, Vc = 1 V, L0 = 0.1 mH); (c) Frequency response of the notch filter (with C0 = 10 uF, R0 = 1 K, Vc = 2V, L0= 0.05 mH); (d) Frequency response of the notch filter (with C0 = 10 uF, R0 = 1 K, Vc = 4 V, L0 = 0.025 mH).
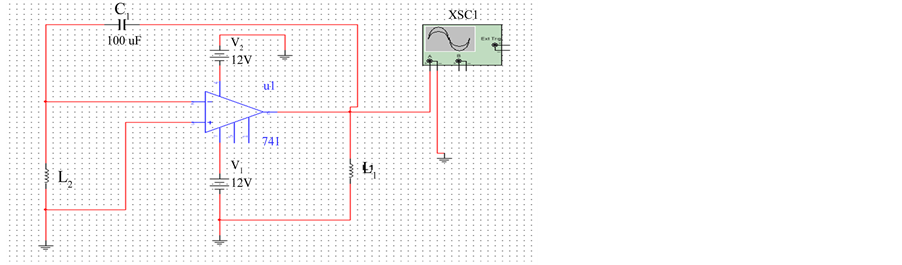

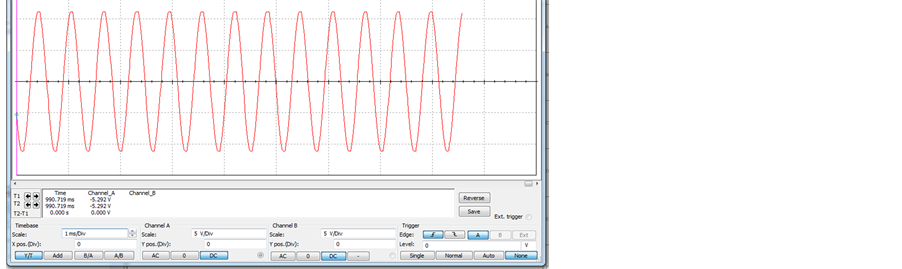

Figure 6. (a) A prototype of op-amp Hartley oscillator; (b) Frequency response of the oscillator (with C = 100 uF, VC = 1 V, L1 = L2 = 0.1 mH) Center frequency =
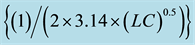
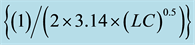

Table 3. Effect of variation in control voltage (Vc) on center frequency (fc) of Hartley oscillator.
Table 4. Comparison of results of reference [17] and proposed realization.
floating inductance, an op-amp and a capacitor. The Hartley oscillator was designed for frequency f0 = 1.125 kHz, 1.59 kHz and 2.25 kHz with different value of inductance as given in Table 3. The center frequency of oscillator was found to be electronically tunable from 1.125 kHz to 2.25 kHz with Vc varying from 1 to 4.
From the above result, it can be seen that by varying the control voltage (Vc) center frequency of oscillation of Hartley oscillator can be changed .Thus we can control the frequency of oscillation by varying Vc.
4. Conclusion
The proposed circuit in Figure 2(a) and Figure 3(a) realized and compared with reference [17] . In Table 4, we
have used less number of CFOAs and less number of passive components. The use of multiplier nullifies the effect of non linearity of FET. The application of BPF, notch filter a Hartley oscillator have been discussed.
Cite this paper
Praween K.Sinha,Dr NeelamSharma,RohitMishra, (2015) A Configuration for Realizing Voltage Controlled Floating Inductance and Its Application. Circuits and Systems,06,189-199. doi: 10.4236/cs.2015.69020
References
- 1. Nay, K.W. and Budak, A. (1983) A Voltage-Controlled Resistance with Wide Dynamic Range and No Distortion. IEEE Transaction on Circuits and Systems, 30, 770-772.
http://dx.doi.org/10.1109/TCS.1983.1085290 - 2. Nay, K.W. and Budak, A. (1985) A Variable Negative Resistance. IEEE Transactions on Circuits and Systems, 32, 1193-1194.
http://dx.doi.org/10.1109/TCS.1985.1085637 - 3. Senani, R. and Bhaskar, D.R. (1991) Realization of Voltage-Controlled Impedances. IEEE Transactions on Circuits and Systems, 38, 1081-1086.
http://dx.doi.org/10.1109/31.83879 - 4. Senani, R. and Bhaskar, D.R. (1992) A Simple Configuration for Realizing Voltage-Controlled Impedances. IEEE Transactions on Circuits and Systems, 39, 52-59.
http://dx.doi.org/10.1109/81.109244 - 5. Senani, R. and Bhaskar, D.R. (1994) Versatile Voltage-Controlled Impedance Configuration. IEEE Proceedings— Circuits Devices and Systems, 141, 414-416.
http://dx.doi.org/10.1049/ip-cds:19941296 - 6. Senani, R. (1995) Universal Linear Voltage-Controlled Impedance Configuration. IEE Proceedings—Circuits Devices and Systems, 142, 208.
http://dx.doi.org/10.1049/ip-cds:19951944 - 7. Ndjountche, T. (1996) Linear Voltage-Controlled Impedance Architecture. Electronics Letters, 32, 1528-1529.
http://dx.doi.org/10.1049/el:19961020 - 8. Leuciuc, A. and Goras, L. (1998) New General Immittance Converter JFET Voltage-Controlled Impedances and Their Applications to Controlled Biquads Synthesis. IEEE Transactions on Circuits and Systems, 45, 678-682.
http://dx.doi.org/10.1109/81.678494 - 9. Senani, R. (1994) Realisation of Linear Voltage-Controlled Resistance in Floating Form. Electronics Letters, 30, 1909-1911.
http://dx.doi.org/10.1049/el:19941313 - 10. Senani, R. (1995) Floating GNIC/GNII Configuration Realized with Only a Single OMA. Electronics Letters, 31, 423-424.
http://dx.doi.org/10.1049/el:19950287 - 11. Kiranon, W. and Pawarangkoon, P. (1997) Floating Inductance Simulation Based on Current Conveyors. Electronics Letters, 33, 1748-1749.
http://dx.doi.org/10.1049/el:19971202 - 12. Abuelmaatti, M.T. (1998) Comment: Floating Inductance Simulation Based on Current Conveyors. Electronics Letters, 34, 1037.
http://dx.doi.org/10.1049/el:19980743 - 13. Layos, M.C. and Haritantis, I. (1997) On the Derivation of Current-Mode Floating Inductors. International Journal of Circuit Theory and Applications, 25, 29-36.
http://dx.doi.org/10.1002/(SICI)1097-007X(199701/02)25:1<29::AID-CTA948>3.0.CO;2-# - 14. Yuce, E., Cicekoglu, O. and Minaei, S. (2006) CCII-Based Grounded to Floating Immittance Converter and a Floating Inductance Simulator. Analog Integrated Circuits and Signal Processing, 46, 287-291.
http://dx.doi.org/10.1007/s10470-006-1624-7 - 15. Elwan, H.O. and Soliman, A. (1997) Novel CMOS Differential Voltage Current Conveyor and Its Applications. IEEE Proceedings—Circuits Devices and Systems, 144, 195-200.
http://dx.doi.org/10.1049/ip-cds:19971081 - 16. Ndjountche, T., Unbehauen, R. and Luo, F.L. (1999) Electronically Tunable Generalized Impedance Converter Structures. International Journal of Circuit Theory and Applications, 27, 517-522.
http://dx.doi.org/10.1002/(SICI)1097-007X(199909/10)27:5<517::AID-CTA76>3.0.CO;2-Y - 17. Senani, R. (1996) Novel Linear Voltage Controlled Floating-Impedance Configurations. ELL/96/53450.