Received 18 February 2015; accepted 9 March 2015; published 11 March 2015

ABSTRACT

A new current feedback amplifier (CFA) based dual-input differentiator (DID) design with grounded capacitor is presented; its time constant (τ_o) is independently tunable by a single resistor. The proposed circuit yields a true DID function with ideal CFA devices. Analysis with nonideal devices having parasitic capacitance (C_p) shows extremely low but finite phase error (θ_e); suitable design θ_e could be minimized significantly. The design is practically active-insensitive relative to port mismatch errors (ε) of the active element. An allpass phase shifter circuit implementation is derived with slight modification of the differentiator. Satisfactory experimental results had been verified on typical wave processing and phase-selective filter design applications.

Keywords:

CFA, Tunable Differentiator, Dual-Input Differentiator, Wave Shaper

1. Introduction

Differentiator and integrator functional blocks find a variety of applications in signal conditioning, wave pro- cessing and shaping, as process controller, phase compensator, and as pre-emphasis unit in radio engineering [1] . A high-quality (q) differentiator with true differential input capability is useful for enhanced signal handling characteristics. The literature shows a number of single-input differentiator circuit design schemes using various types of active building blocks, such as voltage operational amplifier (VOA) [2] - [4] , current conveyor [5] and CFA [6] - [9] .

A new grounded capacitor single resistor tunable true dual-input differentiator design using the CFA-844 building block is presented in this work. The CFA device is essentially a current mode element with improved features compared to the ubiquitous VOA [10] - [12] . The CFA provides unity current gain whereby both voltage-source and current-source output nodes are available such that cascadability for either type of signals is readily realizable. Other versatile properties [12] - [14] of the device relative to analog signal processing functional design, are improved slew-rate, accuracy and effective bandwidth that is nearly gain-independent. Since such a design is not yet reported, it therefore appears appropriate to propose a true dual-input high-q differentiator circuit design based on the CFA device―leading to the motivation of this research work.

Analysis is carried out with both ideal and nonideal models of the device wherein the effects of the finite errors 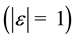in port transfer ratios and parasitic shunt r_pC_p arms appearing at the current source z-node are examined. As per databook [15] , typical values of these shunt components are in the range of 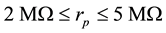and at V.d.c. Albeit effects of ε are seen to be insignificant that of the parasitics introduce finite phase error 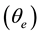which tend to limit the higher side of the usable frequency range. By appropriate design of nominal passive components, the phase error could be minimized without affecting the single tunability feature. The nominal values of circuit resistors are chosen in 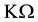range such that their ratios relative to 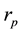are extremely small, and hence may be neglected. The practical performance of the proposed DID had been verified satisfactorily with both PSPICE Macromodel [16] simulation and by hardware tests.

2. Analysis and Design

The CFA based proposed DID topology is shown in Figure 1. The nodal relations of the AD-844 CFA element is 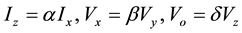and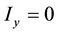; where α, β and δ denote the port transfer ratios. These are usually expressed by some small error 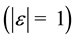terms [8] [17] as and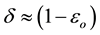. For an ideal device these errors vanish leading to unity transfer ratios. We now present the analysis of the DID circuit assuming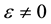; the voltage transfer relation is

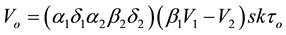(1)

where 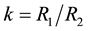and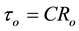. Writing and assuming ideal devices, we get the transfer from Equation (1) as

(2)

Note that no component matching constraint is needed to derive the transfer function in Equation (2) of the DID; time constant may be tuned independently by the grounded resistor (R_o) while additional variation may also be conveniently achieved by ratio-k. With nonideal devices, Equation (1) modifies to

(3)

where. Also the noninverting input signal is slightly reduced by the factor. Literature [8] [13] [17] indicates that error magnitudes are quite low in a typical range of, i.e., hence V₁ input signal degeneration is negligible. The active sensitivity is.

3. Effects of Parasitic Components

Re-examination of the circuit in Figure 1, assuming finite parasitic shunt―components at current source z-nodes of the CFAs, yields the following normalized transfer function

(4)

where and. Since the ratios of nominal resistors with respect to parasitic ones are extremely low, these are neglected. The total phase shift in frequency-re- sponse domain of the DID is therefore

(5)

where; and assuming. Values of parasitic capacitances are in pF range (say 4 - 5 pF) and nominal resistance values are in range (say), by which we may estimate the higher end of usable frequency as

The differentiator quality fator (q) is estimated by writing which defines. From Equation (4) we derive

(6)

Equation (6) may be simplified to obtain a practical value of q after assuming and this yields. The proposed DID therefore offers high-quality feature within a stipulated frequency- range and the design is practically active-insensitive to port errors (ε).

4. Design Application

As an application of the differentiator, we now present the design of a first order allpass (AP) function realization. The differentiator circuit is slightly modified to derive the AP filter as shown in Figure 2; analysis shows constant gain-magnitude (H_o) with variable phase (ψ), given by

(7)

where and gain; these parameters are independently tunable.

With, one gets the non-minimum phase function which yields the phase

(8)

Effects of parasitic capacitances are examined next; re-analysis yields the modified transfer function as

(9)

where and. Thus even with finite para-

sitic capacitances, the circuit provides a non-minimum phase function. Since we get,

hence the phase components of numerator and denominator polynomials in Equation (9) are symmetrical. Writing and, we get the slightly altered phase response as

(10)

The phase response is therefore tunable in the nominal range and is seen to be practically unaffected by. The flat-gain is slightly attenuated at higher frequencies due to the parasitic pole at which may extend upto about 20 MHz as discussed in the earlier section.

5. Experimental Results

Practical responses of both the DID and phase-selective AP filter had been measured using hardware circuit design employing readily available AD-844 type CFA device, and by PSPICE macromodel simulation; these are shown in Figure 3. The DID is tested in time-domain by applying equal but antiphase triangular-wave input signals while its phase-response is observed in frequency-domain, so as to measure at appropriately chosen values of CR_o; these are shown in Figure 3(a) and Figure 3(b). The common mode characteristics of the DID is observed by applying equal amplitude sinusoid inputs while the CMRR had been measured experimentally as equal to 55 dB at 100 KHz and 48 dB at 1 MHz; deviation of the CMRR at higher end of frequency is owing to the noise accentuation property [1] [18] of differentiation function. Measured test response of the AP filter in Figure 3(c) indicates a phase deviation of only at the select frequency of 500 KHz.

Next error estimation is carried out on the magnitude response of the DID for triangular to square wave conversion; these are listed in Table 1 below which shows error on measured output voltage as with being independently tuned by.

6. Conclusion

A new CFA based dual-input high-quality active dual-input differentiator (DID) circuit realization scheme is presented. The advantages of the proposed design are true differentiation function implementation using a grounded capacitor while the time constant is tunable by a single resistor―features suitable for microminiaturization. The gain factor of the circuit may also be conveniently adjusted by a resistor ratio. CFA-based DID design is not readily available in the literature. Such dual-input differentiators are conveniently used as the error- subtractor cum rate controller in a process control loop. All the tunability features of the DID here are independently controllable without requiring any component matching constraint. Analysis with nonideal devices has been carried out which exhibits practically active-insensitive nature of the design. Investigation assuming finite device parasitic indicates certain phase deviation at higher ends of usable frequency range of about 1 MHz. The proposed DID structure is utilized here in the design of a first-order phase-selective allpass function with high input impedance. The phase variation is in the range of which is tunable by a resistor at constant gain magnitude (H_o) adjustable by another resistor ratio. Test response indicates a phase deviation of

Anti-phase triangular wave input signals V₁ = −V₂ = 2 volt(pp) at 1 MHz with k = 1.

due to the device parasitics at the select frequency of 500 KHz. All these responses have been verified experimentally.

References

NOTES

^*Corresponding author.