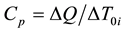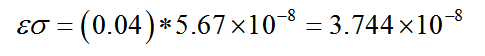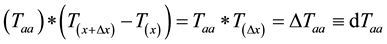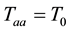Circuits and Systems
Vol.06 No.02(2015), Article ID:54113,8 pages
10.4236/cs.2015.62003
Augmenting the Heat Sink for Better Heat Dissipation
Mohammed H. S. Al Ashry
Department of Computer Science, the Community College, College of Sciences and Humanities, Shaqra University, Shaqra, Saudi Arabia
Email: mashry@su.edu.sa
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 January 2015; accepted 14 February 2015; published 15 February 2015
ABSTRACT
Heat sinks were invented to absorb heat from an electronic circuit conduct, and then to dissipate or radiate this heat to the surrounding supposedly, ventilated space, at a rate equal to or faster than that of its buildup. Ventilation was not initially recognized as an essential factor to thermal dispersion. However, as electronic circuit-boards continued to heat up, circuit failure became a problem, forcing the inclusion of miniaturized high speed fans. Later, heat sinks with fins and quiet fans were incorporated in most manufactured circuits. Now heat sinks come in the form of a fan with fans made to function as fins to disperse heat. Heat sinks absorb and radiate excess heat from circuit-boards in order to prolong the circuit’s life span. The higher the thermal conductivity of the material used the more efficient and effective the heat sink is. This paper is an attempt to theoretically design a heat sink with a temperature gradient lower than that of the circuit board’s excess heat.
Keywords:
Convective Heat Transfer: Heat Absorbed by the Natural Air Flow Surrounding Hot Objects, Forced Convective Heat Transfer: Absorption of Heat Using Forced Air Flow, Conductivity: Is the Ability of a System to Exchange or Transfer Temperature within a Body or Material through the Movement of Electrons, Material That Does Not Conduct Heat Is Considered a Nonconductor

1. Introduction
The way that the heat sink is attached to the circuit-board is a major contributor to the efficiency of its heat conductive-absorptivity. The heat-sink’s ability to dissipate and radiate heat at a rate faster than or equal to its absorbency pace is critical to protect, maintain and extend the lifespan of the circuit. The type of material used for the sink and the juncture is crucial in terms of thermal conductivity, heat capacity, emissivity, resistivity and absorptivity. Heat is absorbed or transferred from a material at a higher temperature to a material at a lower temperature. The greater the temperature disparity among the materials, in the direction from the board to the heat sink on to the surrounding, the faster the pace at which heat is either absorbed or transferred. Heat moves among metals through the diffusion of electrons among atoms until a heat balance between the two contacting materials is established [1] . This transfer of heat is actually a transfer of electrons energy from a more energetic (hot) substance to one that is less energetic (colder) [2] ; this analogy emphasizes contact between the two substances. It is important that the separate substances used are joined together using some form of amalgamation for a complete fusion at the entire circuit-board to heat-sink contact areas. Fusing the substances leads to better transfusion of electrons through the substances. To eliminate the possibility of overheating of either the sink or the circuit board ducted cooling fans scheme is introduced where fans/blowers are positioned in a way that is conducive to increased fluctuating air flow velocity around the heat sink, resulting from the revolving angled fins of the fans and the positioning of the alternating dual fans system. Although the alternating function of the two fans (Figure 1) does not change the eventual constant and consisting air flow velocity, the alternating effects do lower the pressure at the tightening end of the duct. This system allows for a decrease in heat sink’s fins-spacing and its boundary layer thickness, and its fluctuating temperature gradient, and leads to an increase in convection heat-transfer. This leads to a higher rate of cooling of the heat-sink fins and a faster pace of cooling of the circuit board. This scheme, to a certain extent, allows for a reasonably greater height and length in heat sink’s fins.
2. Analysis
Figure 2 provides us with the relationship between heat and heat transfer and its equal in electrical circuits and functions. Heat movement within metals is similar to movement of amps in an electric circuit. Temperature functions in the same way as voltage and thermal resistivity functions like that of electric resistance. So that
 (1)
(1)
Equation (1) displays the heat and ampere equations’ parallelism they are to a certain extent equivalent in form and behavior.
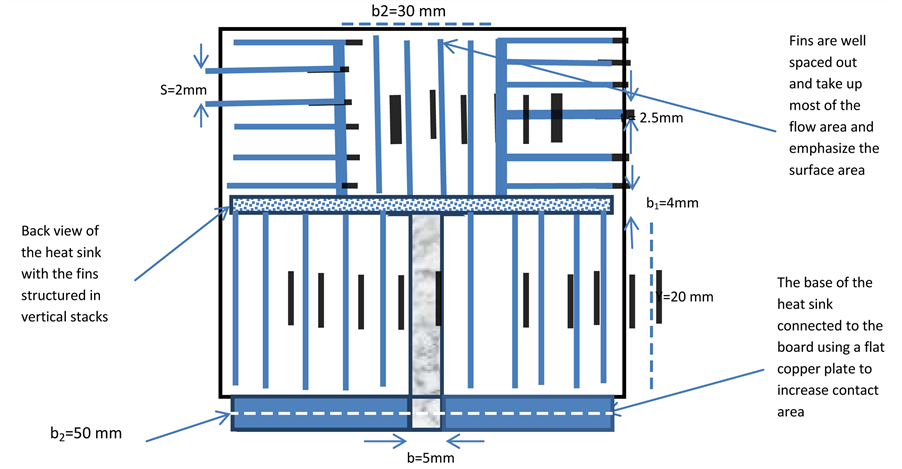
The heat sink design must emphasize a large surface area in order to utilize the forced convection heat transfer induced by the fan-made airflow. Figure 3 displays an approximate view of the heat sink within the exit side of the duct. It is obvious that the heat sink’s back view almost fits into the square shape of the duct vertical to the direction of the flow. However it is a little shorter in the direction of the flow.
Figure 1. The ducted fan and heat sink.
Figure 2. Electrical and thermal circuit analysis of the similarity between heat and electricity [3] .
Figure 3. Back view of the heat sink.
Figure 4 displays a view of the copper plates connecting the base of the sink to the circuit board. The views focus on the plates from top and bottom of the board and its relationship to the base of heat sink. It should be noted that the diagrams are not exact representations of an actual sink.
The heat sink, the base and the juncture are made up of copper. The base and the heat sink are heat-based welded so the heat resistivity between the two parts can be considered equal to the thermal resistivity of copper. The base is attached to the juncture by rolling the plates around the side of the base and using high pressure guns to attach them. The bottom of the base is attached to the plates using high pressure, and beryllium oxide is used to fill the gaps for lower heat resistance and higher thermal conductivity. The thermal conductivity of beryllium oxide (>200) is greater than that of aluminum. This will make it possible for us to neglect under certain circumstances the existence of a ceramic-grease-based gap-filler.
The fans will provide the heat sink with continuous air flow that will lower the temperature of the heat sink and facilitate the transfer and dissipation of heat through the ducted stream. The two fans provide us with many advantages, faster air streaming through the heat sink fins’ spacing due to the vacuuming effect created by the second fan and continuous air flow in case one of the two fans went out; assuming, of course, a fan functional sensor is available and working.
Assuming the fans are timed to alternate that will create the wind tunnel effects of gusting which increases the affected fins’ surface area. The two fans, due to the difference in size will have a different rotational speed and timely alternating flow as follows [4] :
The air volume flux can be calculated using the area of the fan’s opening, and the fans air speed.
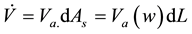


 (2)
(2)
where w is the width of the duct, and L is the length)
Figure 4. Views of the circuit board juncture and sink.
To calculate the gusting of the air movement we have
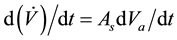 (3)
(3)
The area of the smaller fan is used to measure and gauge its rotational speed in order to attain adequate energy to produce the necessary speed.
The alternation can be timed using a switching control system [5] . The velocity of the air flow will be mostly constant with the exception of the time in which one fan shuts down and the other starts. There are a number of objectives behind this fan design as an option:
1) The increase of air velocity increases the “forced” convective heat transfer;
2) The air speed increases the areas reached by the air flow inside the spacing of the sink’s fins, which in turn increases the functionality of the heat sink, and decreases thermal resistance;
3) This technique supports an increase in the duct’s air pressure over the surface of the sink’s fins; although the design where the duct’s outlet narrows gradually towards the duct’s opening creating a bottleneck effect and increasing the pressure on the sink’s leading edge and inner surface, especially the deep ends of the fins’ spacing on both sides of the sink;
4) A noticeable pressure drop will be noticed at the outlet;
5) The alternating fans create an air flow’s gusting effect that acts as an additional coolant to the sink’s heated surface;
6) This method extends both the life of the computer, its major components including the fans;
7) The system will increase the surface area by allowing for more fins and thinner spacing between the fins.
3. The Approach
The thermal resistance can be obtained using Equation (1)
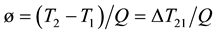 (4)
(4)
Since both the radiation and forced convection heat transfer are active for the sink in our ducted heat sink scheme then starting with forced convective heat transfer we have the following:
Heat transferred out of the sink is measured on the basis of the temperature difference between the heat sink- fins’ surfaces and the surrounding:
 (5)
(5)
But the convective heat transferred to the surrounding seeps through the sink’s bases and fins where their positioning and attributes, length, height, angles, thickness and spacing, have a lot to do with the heat exchange. Figure 1 and Figure 3 are essential to the rest of this paper. The formula for the convective heat exchange is
 (6)
(6)
where 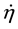 is the fins efficiency coefficient
is the fins efficiency coefficient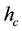 , is the heat transfer coefficient and
, is the heat transfer coefficient and 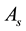 is the fins surface area, and the temperature difference between the outlet and inlet of the duct
is the fins surface area, and the temperature difference between the outlet and inlet of the duct
But since 

We know that 
However, we know that the quantity of heat absorbed by the air is:

But since the thermal resistivity is dependent on the fins’ surface area and type of material we have
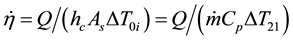
We know that heat capacitance
and air mass flux rate

with density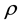


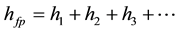
and for fins in series
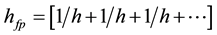
Respectively we have

where
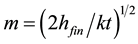
Then

where 


The second channel of emitting heat through the heat sink is the radiation of heat through the fins which is influenced by the material used, emissivity and the energy radiated by a surface in relationship to a black body.
where

The heat transfer coefficient of radiation 
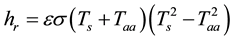
Where 

The Boltzmann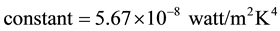
The thermal resistance in the radiation case is inversely proportional to both the surface area 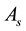
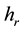
Now it is a good idea to go back to the thermal resistance of the heat between the circuit and the heat-sink’s surrounding where total thermal resistance between the sink-circuit board-juncture and the air surrounding the heat sink
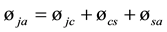
but

Equation (18) shows the need for a high dissipative outlet to prevent over heating however the unknown in this case is the added element that is not made obvious by Equation (15), the forced-convective heat transfer dispersing heat through cooling of the fins surface by the high, double-fanned air flow velocity.
The total rate of convective and radiative heat transfer for the entire heat sink fins is

Assuming we have 


where 

Now consider Equation (20) again where
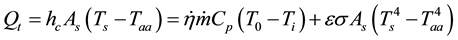
In Equation (23) however, radiation is ignored and Table 1 provides us with reasonable rationale to do so.
This means that only a small percentage of the heat transferred from the surface of the sink is done through radiation, and considering the radiation heat Equation (16) we can tell that 
Table 1. Radiation deficiencies in finned heat sinks.
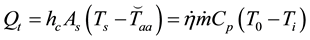
Now the ambient temperature 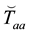
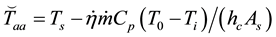
If we set Equation (25) equal to zero, and differentiating over the distance before and after the sink, and assuming constant air speed (velocity), which means that the mass flow rate ṁ, is also constant, also assuming constant heat transfer coefficient

by dividing both sides by the total heat transfer we get
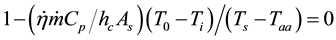



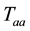

where
and by integrating over the duct’s length over the perimeter of the sink we have
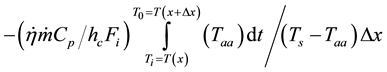
where, in this case 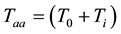
Equation (26) becomes


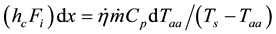
Using the integration process
We have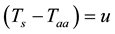


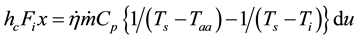
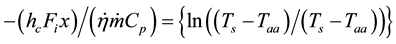

Using log rules

Now we can get the average ambient temperature, which we already assumed to be equivalent to the average temperature across the duct in air flow direction:

At 
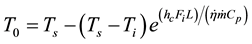
To get the average ambient temperature
We use Equation (39) in Equation (25) to get


Now we can get the total heat transfer by using Equation (41) in Equation (24) to get

Now it is obvious that the difference in temperature between the sink temperature and the inlet can be used to derive the total juncture to ambient thermal resistance. And it can also be assumed that the difference between the sink’s temperature and the outlet temperature can be used to derive the radiative heat transfer. The difference between the two thermal resistances is the forced convective thermal resistance.
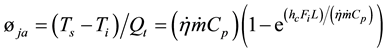
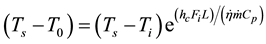
The ratio of radiative to total heat transfer is

And so

Based, of course, on the material’s high thermal conductivity, however, its dissipative-dispersive and radiative attributes are due not only to its above mentioned heat transfer qualities, but also due to the forced-convective heat transfer feature [7] . Experiments [8] have proven that increasing convective air flow velocity by 70 percent, decreases conductive resistance by 75 - 80 percent on the surface of the heat sink. This feature is very compelling and puts emphasis on the utilization of forced convective air flow.
4. Conclusion
The heat sinks are neither expensive nor difficult to design or manufacture. The major aspect in heat sinks’ design is sampling of the parts in central areas within the circuit board for better easier access to the heat source for better absorption. Central areas within circuit boards are not easily accessible for heat sinks’ fusing and sampling. The central circuit-board locations’ inaccessibility is a bit challenging to electronic designers when attempting to link the separate parts together for better and faster bussing and data communication. The right heat sink in the right spot within a circuit board facilitates heat conductivity-absorption and dissipation, and extends the life span of the board and its major components. The dual fan design keeps a constant air flow, infiltrates the heat sink’s narrow fins’ spacing, increases surface area, leads to higher convective heat transfer, and reduces pressure at the outlet. The design is made to force the air into the inner regions of the fins’ spacing, and the outlet fan alleviates the pressure build up-forward to the sink. I recommend this system for high heat circuit-boards.
References
- http://WATLOW.COM
- http://encyclopedia2.thefreedictionary.com/thermodynamics+processes
- Lee, S. How to Select a Heat Sink. Advanced Thermal Engineering, Aavid Thermal Technologies, Inc., Laconia.
- Hamburgen, W.R. (1986) Optimal Finned Heat Sinks. Digital Equipment Corporation, Western Research Laboratory, Palo Alto.
- Sridhar, R. (2011) Discretization of Convection-Diffusion Type Equation. 10th Indo-German Winter Academy, Indian Institute of Technology, Madras.
- ICT International Pty Ltd. Theory of Emissivity. DocRef: Ver 1.1, Armidal NSW 250, Australia. www.ictinternational.com.au
- Qu, W. and Mudawar, I. (2002) Analysis of Three Dimensional Heat Transfer in Micro-Channel Heat Sinks. School of Mechanical Engineering, Purdue University, West Lafayette.
- Haskel, M.D. Thermal Resistance Comparison of Graphite Foam, Aluminum, and Copper Heat Sinks. http://www.electronics-cooling.com/2006/02/thermal-resistance-comparison-of-graphite-foam-aluminum-and-copper-heat-sinks/