Received 2 August 2014; revised 24 August 2014; accepted 2 September 2014

ABSTRACT

In this paper a comparison of a sixth-order active band pass R-filter output response with the output response of a sixth-order band pass RC-filter at different quality factors (Q = 2, 5, 7, 8 and 10) was carried out at a fixed frequency of 10 KHz. The architecture used in the design is the mul- tiple feedbacks for both filter networks. The simulated response characteristics show that both filters (R- and RC-filters) have their mid-band gains increasing with Q, while their bandwidths mo- notonically decreased with Q-values. The bandwidths are in the range of 22.23 dB to 62.97 dB and −55.49 dB to −50.81 dB (Q = 2 to 10) for R- and RC-filters respectively. At higher Q-values, R-filter showed better selectivity with a smaller bandwidth (400 Hz) at the edge of the pass band, when compared to 450 Hz for the RC-filter. The roll-off rate around −58.9 dB/decade for the R-filter ap- pears to be that of a third-order filter response, while the RC-filter has its response in the range −106 to −132 dB/decade which is in the neighbourhood of an ideal sixth-order response (roll-off of 120 db/decade). A shift in the center frequency with Q was observed for the RC-filter only.

Keywords:

R-Filter, RC-Filter, Gain, Roll-Off, Multiple Feedback, Sixth-Order Filter

1. Introduction

In modern electronic circuits, unwanted signals are a major challenge to contend with. This is due to interferences in the form of noise and harmonics. These unwanted signals pose problem to certain specified desired bands of frequencies. In many state-of-the-art equipment or systems, such as receivers, EEG and FDM etc., high quality factors and fast roll-off rate filter networks are used to select/reject or separate/combine signals at different frequencies [1] . The common filters are the resistance-inductance-capacitance (RLC) based-filter networks. Others are the switched capacitor based filters using MOS switches rather than resistors or inductors. At high frequencies (≥1 MHz), inductance based filters are favourable, but become bulky and expensive at low-medium frequencies (≤1 MHz). The RC-filters utilizing operational amplifiers as active element and resistors and capacitors as passive elements are best suited for low-medium frequency responses. However, high quality capacitors having superior stability characteristics are also expensive and large in size, while physically small capacitors such as ceramic capacitors, exhibit relatively poor stability characteristics [2] [3] . These smaller capacitors when used as part of the filter capacitance may cause the filter to be highly Q-sensitive to circuit element value changes and thus exhibit unstable or severe amplitude peaking or attenuation [2] .

The development of capacitor-less filter (R-filter) network has eliminated these bulky components (thereby reducing cost of production) and has also enhanced the stability of the filters. The building block of the R-filter is the internally compensated operational amplifiers (Op-Amps) [4] [5] . In addition to frequency stabilization by the R-filter network, it also has the potential advantages of miniaturization, ease of design and high frequency performance [6] - [8] . Active R-filters have been reported to be suitable for medium-Q high frequency applica- tions [9] . The major disadvantages of the active R-filters were the temperature dependence of the filter centre frequency and the limited dynamic range due to Op-Amp slew rate limitations [10] . These disadvantages have been overcome by applying the active-R technique to current-feedback Op-Amps [10] .

Although, several papers have reported on the evaluation of the second-and third-order active R-filters [11] - [13] , we have not come across any reported circuit regarding direct cascading of circuits for the realization of higher-order active R-filter network and its comparison with an equivalent RC-filter network. This paper there- fore, is an attempt to design and simulate the sixth-order R- and RC-filter networks and to compare their fre- quency response characteristics based on their quality factors variation. It is not in doubt that higher-order filters provide higher gains as well as better frequency selectivity [14] .

2. Methodology

2.1. The R- and RC-Networks

The architecture that was used to implement both the sixth order active R-band pass filter and the sixth order active RC-filter is the multiple feed-back topologies. This topology was realized by cascading second order band pass filters of Figure 1 (stage 1 with single Op-Amp A1) and Figure 2 (stage 1 with operational amplifiers A11 and A12)

for RC- and R-band pass filters respectively. All operational amplifiers (Op-Amps) are of the 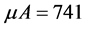type of unity-gain frequency. The implementation of the designed filters utilized the 741 operational amplifiers, 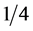watt resistors with 5% tolerance and ceramic capacitors.

2.2. Theoretical Consideration of Band-Pass RC-Filter Network

Figure 1 presents a second-order band pass filter in a multiple-feedback configuration cascaded in three stages to form a sixth-order band-pass RC-filter network. The voltage divider at the input of stage 1 for example, consists of resistors 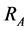and 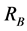which serves as input attenuator to reduce gain. The voltage transfer function of a single stage of the filter network shown in Figure 1 can be expressed as [15] :

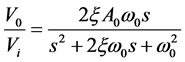(1a)

or in terms of quality factor, [9] :

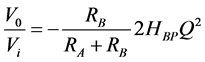(1b)

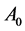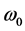where and are the band-pass gain and open-loop 3 dB frequency (is gain band-width pro- duct) of the operational amplifier 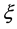is the damping factor and

(1c)

The quality factor, 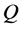and the frequency in Equation (1) are given by Equations (3) and (4) as follows:

(2)

(3)

From Equations (2) and (3), is the capacitance of the capacitor, which is assumed to have equal values, that is, and. The resistors, , and are related to the quality factor by the Equation (4),

(4)

Design of Second-Order Band-Pass RC-Filter Network

The design parameters are that the filter should have a constant resonant frequency of 10 KHz at quality factors of 2, 5, 7, 8 and 10, respectively. First, we consider the design with a center frequency of 10 KHz and. Also, for the purpose of simplification, we assume the capacitors have equal values of. Therefore, from Equation (3), the value of resistor, is calculated to be

Using Equation (4) and choosing, was calculated to be 1999 Ω (2.0 kΩ). The open loop band pass gain was calculated using Equation (1) to be −40 dB (or 0.01).

Similar procedure was used to determine the resistor values, , and for high quality factor, 7, 8, and 10. All calculated resistor values and their respective experimental values chosen for the implementa- tion of the second order RC-filter are presented in Table 1. To obtain a sixth-order RC-band pass filter, the sin- gle second-order filters designed above were cascaded as shown in Figure 1 and implemented using Multisim Electronic Workbench software.

2.3. Theoretical Consideration of Band-Pass R-Filter Network

Stage 1 of Figure 2 shows the second-order band pass R-filter used in this work to design the sixth-order band- pass R-filter configuration. The circuit was proposed by Shinde and Patil [5] . The second-order band-pass R- filter network in Figure 2 has a voltage transfer function:

(5a)

or in terms of quality factor,.

(5b)

where is the gain-band width product of the operational amplifier, and are the attenuators formed by the voltage divider networks of resistors and (and) and given in Equations (6a) and (6b):

(6a)

(6b)

The second-order band pass R-filter network in Figure 2 has resonance frequency, and mid-band gain, given by Equations (7) and (8), respectively

(7)

(8a)

But from Equation (6a),

(8b)

Therefore, from Equations (8a) and (8b) the gain, can be simplified as follows:

(9a)

For cascaded band-pass R-filter with multiple feedbacks, the gain can be expressed as:

(9b)

From Equations (7) and (8), it can be seen that the resonance frequency is dependent on the voltage divider network formed by and at the non-inverting inputs of the two Ops, while the mid-band gain can be tuned by the voltage divider formed by and at the inverting input of the second Op.

Design of Second-Order Band-Pass R-Filter Network

First, we consider the design of second-order band pass R-filter (stage 1) with resonant frequency of 10 KHz, and [16] . Choosing from Equation (7) we have (choose 100 KΩ). From Equation (8b) and taking the value of as 10 KΩyield. The value of filter gain calculated from Equation (9) is 1.73 (4.76 dB). All calculated component values are presented in Table 2. The experimental values (with 1% tolerance) used to realize the band pass filters are also presented in Table 3.

Similar calculations for the component values were carried out using Equation (7) to (11) for higher -va- lues (, 7, 8, and 10) with constant center frequency. To realize a sixth order configuration, the second order filters was cascaded as shown in Figure 2 and implemented using Multisim Electronic Work bench software.

3. Results and Discussion

Figure 3 shows the magnitude verses frequency response plot obtained from the output of the three cascading sections (stages 1, 2 and 3) of the sixth-order band pass R-filter with. The plot shows a gradual increase in the mid-band gain and roll-off of the R-filter network obtained from the output of the first cascading section

(stage 1) to the third section (stage 3). The band-width was however found to decrease monotonically with each additional section. From the result of the roll-off presented in Table 3, it seems each cascading section is pro- viding a single pole roll-off of According to Jecob [17] , the total roll-off of n iden- tical first order sections in cascade is given by:

(11)

Thus, for the three cascading stages (Figure 2), and the result in Table 3 shows consistency with the above argument. This observation is contrary to report by Shinde et al. [8] that each section is a two pole net- work. The total roll-off of the R-filter network in Figure 2 is close to the ideal value of for a third-order configuration (Figure 3 and Figure 4, Table 3). This is however not the case with the magni- tude-frequency response of the sixth-order RC-filter configuration presented in Figure 5. The values (Table 4) approach that of the ideal sixth-order network given by [18] . A modification of Figure 4 to provide higher roll-off without the addition of a single component is possible as observed from a preliminary work carried out by these authors. The higher roll-off for the RC-filter network occurred in fre- quency band of no interest and parasitic effects are therefore “suspects” [19] .

The magnitude response of the cascaded R- and RC-band pass filters (for, 5, 7, 8 and 10) are presented in Figure 4 and Figure 5, respectively. Both filter configurations show monotonic variations in the band-pass gain and band-width with increasing Q-values (see also Table 4). The highest mid-band gain and smallest band-width response was recorded for both R- and RC-filters for, indicating better selectivity at higher quality factors. This observation is consistent with previous reports [14] . However, it is worth nothing that the R-filter network provided a positive gain and smaller band-width (Figure 4) when compared to the RC-filter network (Figure 5) at corresponding Q-values. This clearly suggests that the R-filter network provided better selectivity than the RC-filter network. Also, we observed a relative shift in the center-frequency towards lower frequencies with increasing Q-values for the RC-filter network (Figure 5), but the centre frequency

remained fixed for the R-filter network (Figure 4). It is reported that higher Q values (e.g.) create cir- cuit instability and makes the circuit very sensitive to circuit component tolerances [2] . According to Attri [2] , capacitors are the real accuracy controlling and variation controlling components and so, precise capacitors are required in a multiple feedback topology (MFB) like the one presented in this work. Apart from the capacitors, the MFB topology is particularly very sensitive to the tolerance of the attenuator resistance RB and so requires precise resistors. Thus, the shift in the center frequency (particularly at) can be attributed to the high to- lerance values of the resistors and the approximated values of resistors used in this design. The restriction to the commonly available resistor informed these approximations. These challenges are however absent in the ac- tive-R filter topology considered in this work thereby making it a better choice when compared to the RC-filter in the MFB topology.

4. Conclusion

We have successfully designed and compared the band-pass responses of higher-order R- and RC-filter net works and found that in addition to the advantages of miniaturization, ease of design and high frequency per- formance, the R-filter network provides better selectivity, greater stop band attenuation and steeper cut-off at the edge of the pass band especially at higher Q-values. Also, no relative shift of the centre frequency was observed with R-filter network unlike the RC-filter network which had a relative shift of its centre frequency with Q. The low roll-off rate recorded for the three cascading sections of the R-filter indicate a third order configuration ra- ther than the proposed sixth order. Nevertheless, the three cascaded network can be modified to provide higher roll-off when desired.

References