Circuits and Systems
Vol. 3 No. 2 (2012) , Article ID: 18551 , 7 pages DOI:10.4236/cs.2012.32016
Dynamic and Leakage Power Estimation in Register Files Using Neural Networks
American University of Sharjah, Sharjah, UAE
Email: {asagahyroon, jabdalla}@aus.edu
Received October 25, 2011; revised January 16, 2012; accepted January 24, 2012
Keywords: Component; Formatting; Style; Styling; Insert
ABSTRACT
Efficient power consumption and energy dissipation in embedded devices and modern processors is becoming increasingly critical due to the limited energy supply available from the current battery technologies. It is vital for chip architects, circuit, and processor designers to evaluate the energy per access, the power consumption and power leakage in register files at an early stage of the design process in order to explore power/performance tradeoffs, and be able to adopt power efficient architectures and layouts. Power models and tools that would allow architects and designers the early prediction of power consumption in register files are vital to the design of energy-efficient systems. This paper presents a Radial Base Function (RBF) Artificial Neural Network (ANN) model for the prediction of energy/access and leakage power in standard cell register files designed using optimized Synopsys Design Ware components and an UMC 130 nm library. The ANN model predictions were compared against experimental results (obtained using detailed simulation) and a nonlinear regression-based model, and it is observed that the ANN model is very accurate and outperformed the nonlinear model in several statistical parameters. Using the trained ANN model, a parametric study was carried out to study the effect of the number of words in the file (D), the number of bit in one word (W) and the total number of Read and Write Ports (P) on the values of energy/access and the leakage power in standard cell register files.
1. Introduction
Reducing the energy consumption of modern processors is critical to the extension of battery life time in portable devices. Various studies have shown that register files are major consumers of energy in modern processors [1- 3]. Different architectures and techniques have been proposed in the literature [4-9] where the primary objective was to optimize the energy consumption of register files. Hence, there exists a justifiable need for the accurate power modeling of these components taking into consideration the current nanometer processing technologies. Different modeling techniques have been discussed in the literature but mostly assuming micrometer technologies; a discussion of the various modeling approaches and their advantages and shortcomings can be found in [10,11].
In recent years, there has been a great advancement in the field of ANN, both from theoretical and applications points of view. ANN has been used in classification, pattern matching, pattern recognition, optimization and control-related problems. In electrical engineering, neural networks have been used to solve a wide variety of VLSIrelated problems [12-16]. A neural network (NN) approach for modeling the time characteristics of fundamental gates of digital integrated circuits that include Iinverters, NAND, NOR, and XOR gates is discussed in [2]. The modeling approach presented in the article is technology independent, fast, and accurate, which makes it suitable for circuit simulators. The application of an artificial neural network (ANN) to the study of the nanoscale CMOS circuits is presented in [13]. A novel method of testing analog VLSI circuits, using wavelet transform for analog circuit response analysis and artificial neural networks (ANN) for fault detection is proposed in [14]. Power consumption using neural network of analog components at the system level is discussed in [15]. The method provides estimation of the instantaneous power consumption of analog blocks. In [16], the authors proposed an ANN-based approach for modeling performance of nano-scale CMOS Inverters. The inputs to the network are the channel width of the PMOS and NMOS transistors and the load capacitor. The outputs are rise time and fall times of the output, inverter switching point, and average power consumption.
In this work, we propose the use of neural networks in modeling energy/access and leakage power of standard cell based register files designed using 130 nm technologies. Three parameters that influence the power consumed by a register file, namely, the number of words in the register file (Depth), the number of bits in one word (Width), and the total number of Read and Write Ports (Port) are used as inputs to the ANN. The output parameters of the ANN are the energy/access and the leakage power. To the best of the authors’ knowledge this is the first work that attempts to create power models for register files using ANN.
2. Background
In their work, Praveen and others [10], used low level simulation that takes into account the layout details as well as detailed transistor characterization provided by a standard cell library to collect data on the power consumption of various structures of register files. They used optimized Synopsys Design Ware components from the UMC 130 nm library to design various register files structures. Layouts were generated for register files with a varying number of ports ranging from 3 to 12, a depth that varies from 4 to 64 words, and a width that varies from 8 to 128 bits. All these combinations of register files were designed; patristic capacitances in the routing wires and gate capacitances of each transistor were extracted from the layouts. The extracted netlist was then simulated using ModelSim with different switching activity factors to obtain power estimates. After completing over 100 register file design for the 130 nm technology node, the dynamic and leakage energy of each design was tabulated. Curve fitting was performed on each variable using register file depth, width, number of ports as well as the activity factor as independent input variables. For the designs it is assumed that each of the ports of the register file is driving a load of F04. To a first degree of approximation and to keep the problem tractable, the authors assumed that the energy/access scales linearly with the Hamming Distance between consecutive read/ written words. The assumption is validated using different Hamming Distances. Equations (1) and (2) below are the derived model equations, where Energy/Access and Leakage power are the subjects of the two equations respectively; the authors in [10] referred to it as the Empire Model. For a complete description of the steps taken to arrive to this model, readers are referred to [10].
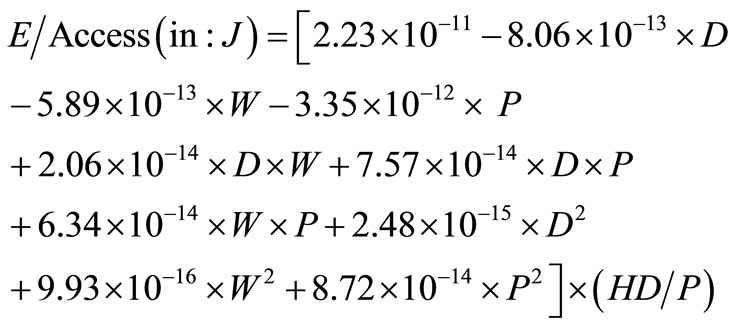 (1)
(1)
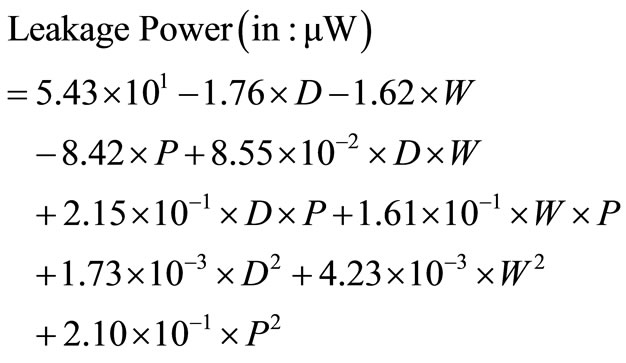 (2)
(2)
In the equations above: D represents the number of words in the file, W represents the number of bit in one word, P represents the total number of ports (read and write), HD is the total number of bits that switch (either from 1 to 0 or from 0 to 1) on the data and address lines from one read/write cycle to another.
To validate the curve-fitted formulae described by Equations (1) and (2), they were compared against results obtained using low level detailed implementations. It is reported that the Empire models exhibit on average about 10% error when compared to the values obtained using detailed simulation.
In this work, data sets obtained from detailed simulation using the power estimation framework proposed in [10] were used to train and test the proposed ANN model. The performance of the ANN model is compared with results obtained using Empire model, as well as power measurements obtained using detailed low-level design simulations of the register files.
3. Neural Network Model and Architecture
The field of Artificial Neural Networks is one of the main branches of artificial intelligence that found many applications in several engineering disciplines. ANNs are processing elements that are capable of learning relationships between input and output and they can be used for classification, prediction, clustering and function approximation, among others. Several neural network architectures with different learning algorithms such as backpropagation were used over the years. In general, an ANN consists of massive parallel computational processing elements (neurons) that are connected with weighted connections and have learning capability that simulates the behavior of a brain [17]. The network weights and the network threshold values are initially set to random values and new values of the network weights and bias values are computed during the network training phase. The neurons output are calculated using Equation (3) below:
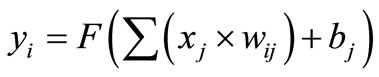 (3)
(3)
where yi is the output of the neuron i, xj are the input of j neurons of the previous layer; value, wij is the neuron weights, bj is the bias for modeling the threshold; and F is the transfer or activation function [17,18]. The transfer function also known as the processing element is the portion of the neural network where all the computing is performed. The activation function maps the input domain (infinite) to an output domain (finite). The ANN Error (E) for a given training pattern i is given by Equation (4):
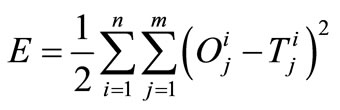 (4)
(4)
where 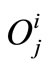 is the output and
is the output and 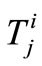 is the target. For a thorough discussion of neural network theory and applications readers are referred to [17].
is the target. For a thorough discussion of neural network theory and applications readers are referred to [17].
The Radial Basis Function (RBF) ANN together with the Gaussian activation function, and the Multi-Layer Perceptron (MLP) together with the hyperbolic tangent (tanh) activation function are among the most widely used feed-forward universal approximators. In this study a hybrid of these two universal approximators is used. Specifically, a RBF ANN topology with one additional hidden layer and 15 neurons (processing elements) in first hidden layer, and four processing element in the second hidden layer are used. The RBF neural network has a Gaussian activation function in the first hidden layer while the additional hidden layer has a tangent hyperbolic (tanh) activation function and the output layer has a bias axon activation function as shown in Figure 1. The performance of this combination of activation functions for the data set used in this work proved to outperform the standard RBF or standard MLP, when used separately.
As depicted in Figure 1, the neural network architecture used in this study, has one input layer, two hidden layers and one output layer. The input layer consists of three nodes, mainly, the number of words in the register file Depth (D), the number of bits in one word Width (W), and the total number of Read and Write Ports (P). The output layer of the ANN consists of two nodes which are the energy/access, and the leakage power as shown.
The data collected from the detailed simulation runs is divided into two categories referred to as the training data, and the test data. The training of the network is conducted using the training data set. The test data is used to validate the performance of the network by comparing its outputs with the values reported from the detailed simulation of the register files design. Table 1 shows the range of maximum and minimum values of the training and testing data sets that is used in this study. The ranges of Energy/Access and Leakage Power indicate the minimum and maximum values reported from detailed simulation results within each selected category. Initial random values are used for the weight of the neural network and different learning rates (step sizes) were used for the different layers of the RBF neural network. The learning rate used for the first and second hidden layers is 1.0 and for the output layer is 0.1. A momentum factor of 0.7 was used for the model all through. The total number of data items used for training the neural network is 60, and the number of data items used for testing the neural network is 20. The neural network was trained 20 times with 2000 epochs in each training cycle and the average performance was recorded. The average minimum normalized mean square error (NMSE) for the training data was 0.00045 with standard deviation of 0.00019.
4. Results and Discussions
In this section we discuss results of power estimates obtained using the following:
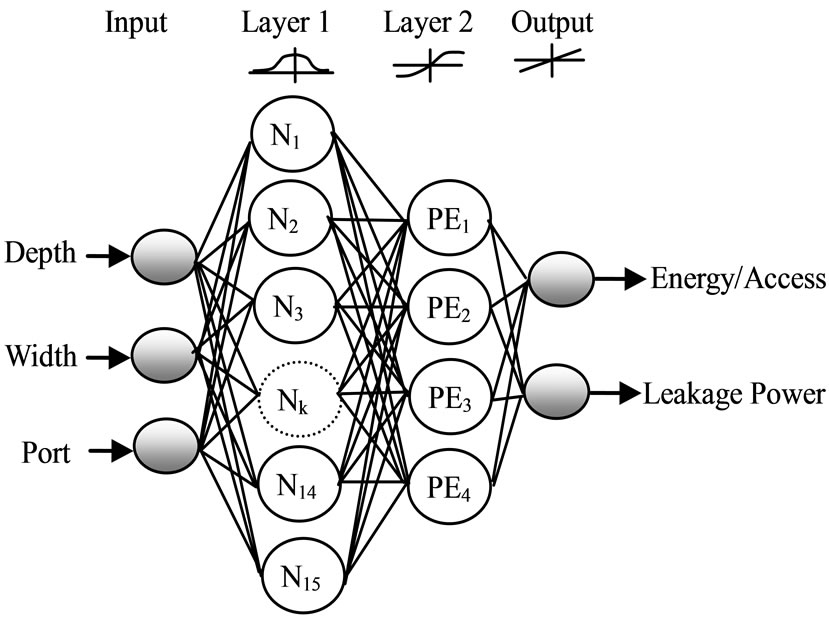
Figure 1. A multilayer RBF neural network topology.
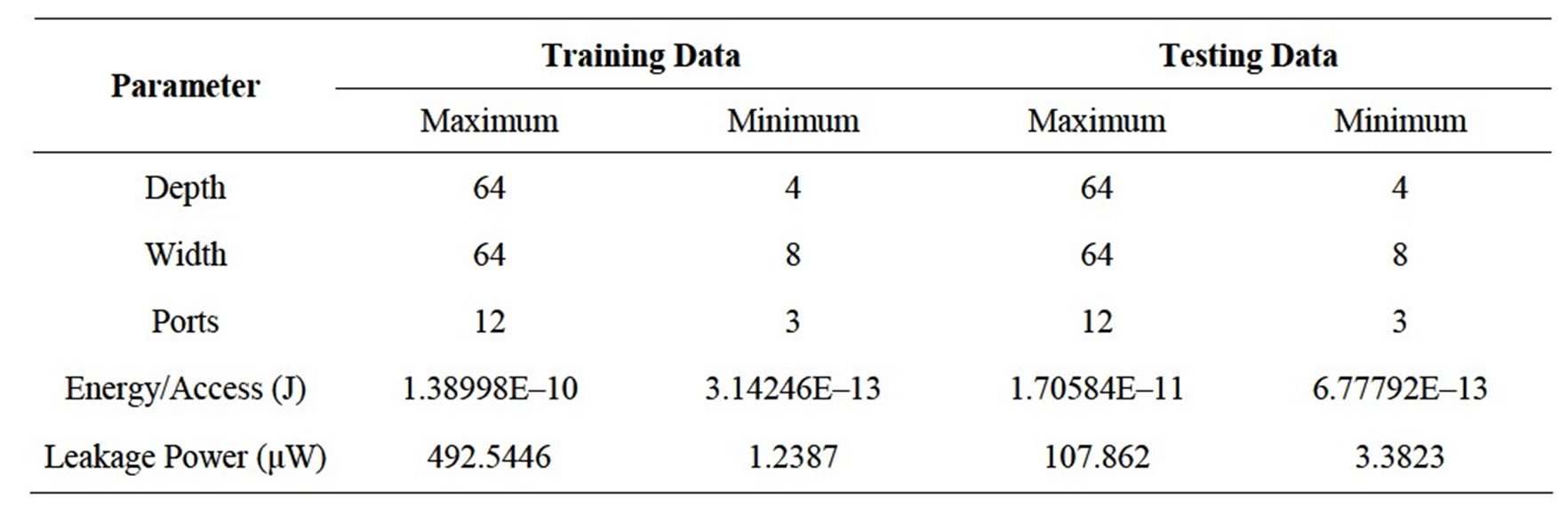
Table 1. Range of training and testing parameters.
1) Empire Model (Empire Prediction);
2) ANN Model (ANN Prediction);
3) Detailed simulation-based power measurements (Experimental Values).
The ANN model was trained using 60 data sets, and for verification the trained ANN model is tested on 20 randomly selected testing data sets. Tables 2 and 3 show the performance indicators of the 20 testing samples for the two outputs (Energy/Access and Leakage Power) respectively. As shown in Table 2, for the Energy/Access, the normalized mean square error (NMSE) obtained is 0.05951 and the correlation co-efficient (r) is 0.97445, while from Table 3 for Leakage Power, the normalized mean square error (NMSE) is 0.045778 and the correlation coefficient is 0.9823. This indicates that the measured and the ANN predicted values correlate very well for both parameters. It is clear from the tabulated results that the ANN model outperformed the Empire model in all performance criteria.
Figures 2 and 3 show the prediction and accuracy of the ANN model and the Empire model based on the test data set when compared to the detailed simulation values of energy/access and leakage power. The ANN prediction is clearly better than the prediction computed using the Empire model.
It is observed that 75% of ANN model predictions of the test data are within 10% of the measured values of energy/access compared to only 15% of Empire model predictions of the test data are within 10% of the measured values of energy/access. Also, 75% of the ANN predictions of the test data are within 20% of the measured values of the leakage power while only 30% of Empire model predictions of the test data are within 20% of
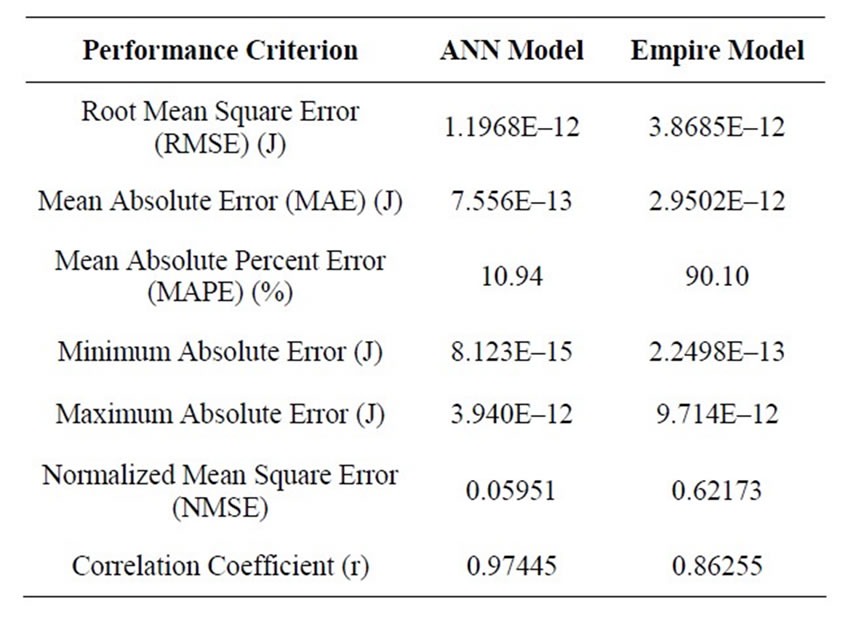
Table 2. Performance of the ANN prediction of energy/ access on the test data.
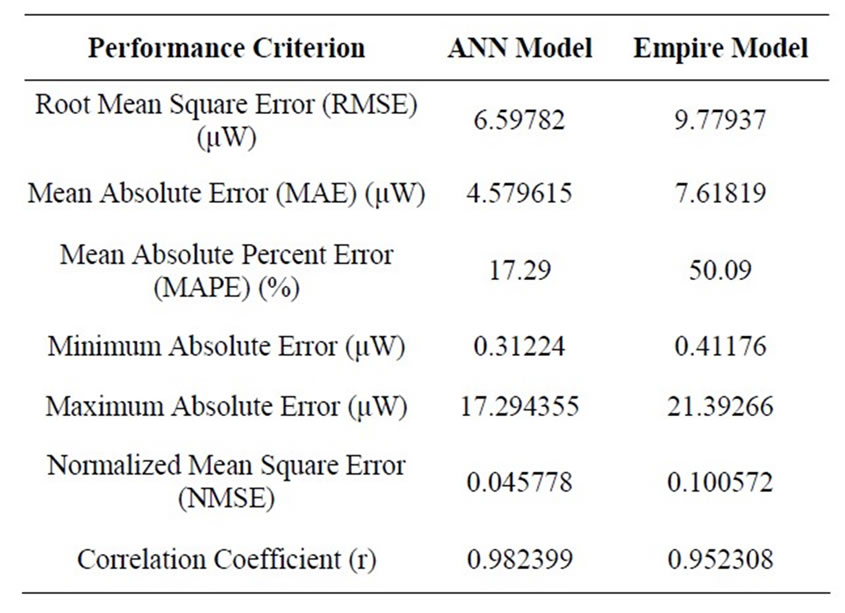
Table 3. Performance of the ANN prediction of leakage power on the test data.
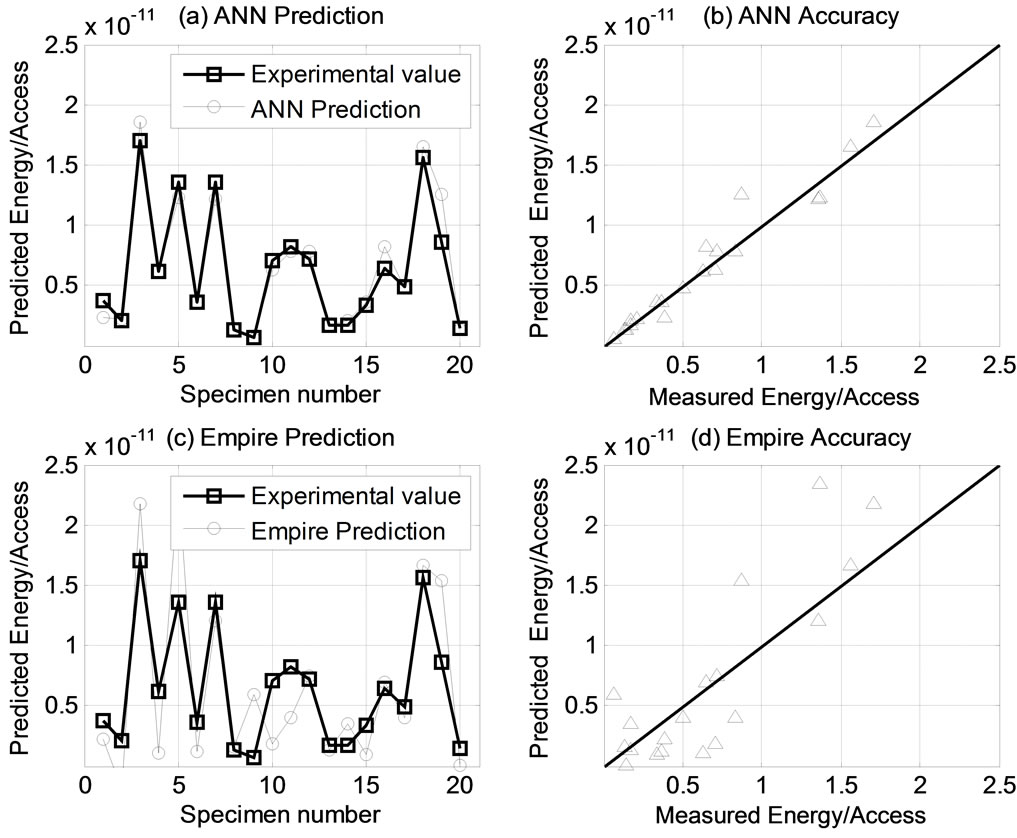
Figure 2. Prediction and accuracy of energy/access using test data.
the measured values of leakage power. Furthermore, some of Empire predictions have relative percent error well above 100%.
5. Parametric Study
To further compare the performance of the Empire model and the ANN model in predicting the Energy/Access and the Leakage Power, we varied the input parameters (width, ports, and depth) and computed the resulting outputs. Figures 4 and 5 depict comparative plots showing the predictions of energy and power respectively. From Figure 4(a), Empire seems to overestimate the Energy/Access prediction for wider designs with relatively fewer ports since from Figure 4(b), the estimates of both models for 32 ports is closer. Similar overestimates occurred when the number of ports and depth is varied (Figures 4(d) and 4(e)). Interestingly from Figure 4(f), the Empire model underestimated the energy per access in the case of wider and deeper designs.
From the plots of Figure 5, the performance of the two
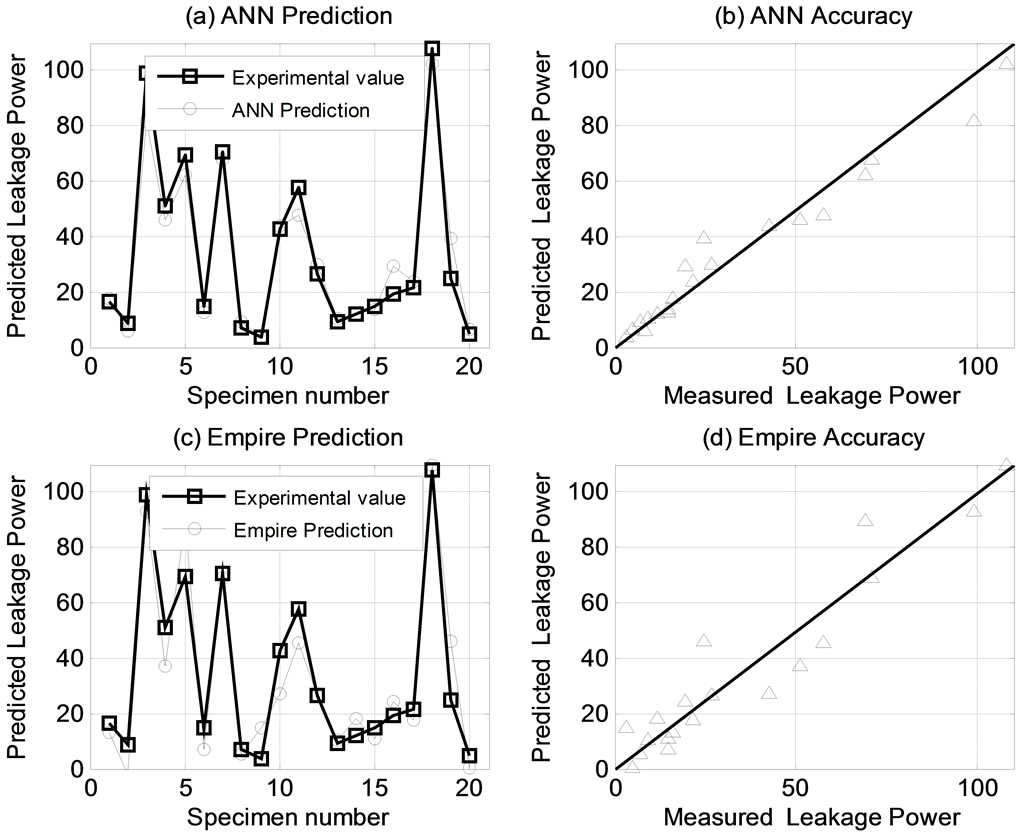
Figure 3. Prediction and accuracy of leakage power of test data.
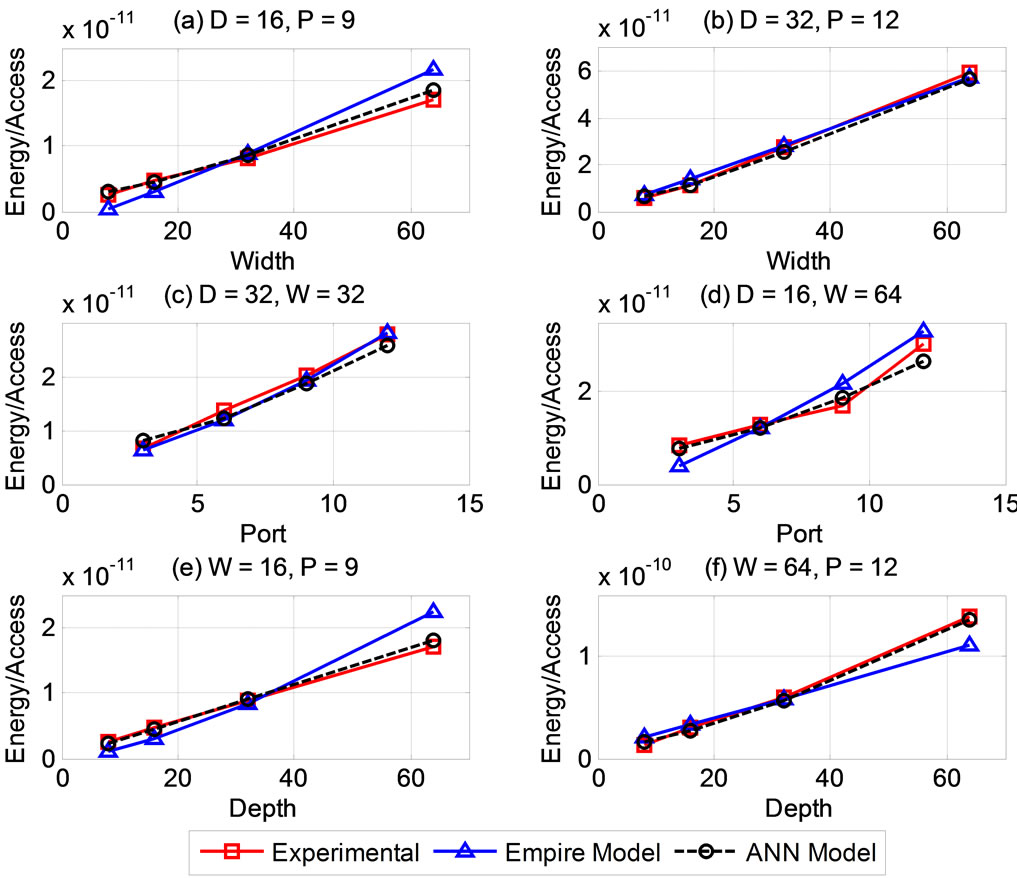
Figure 4. Comparison of energy/access for selected register files.
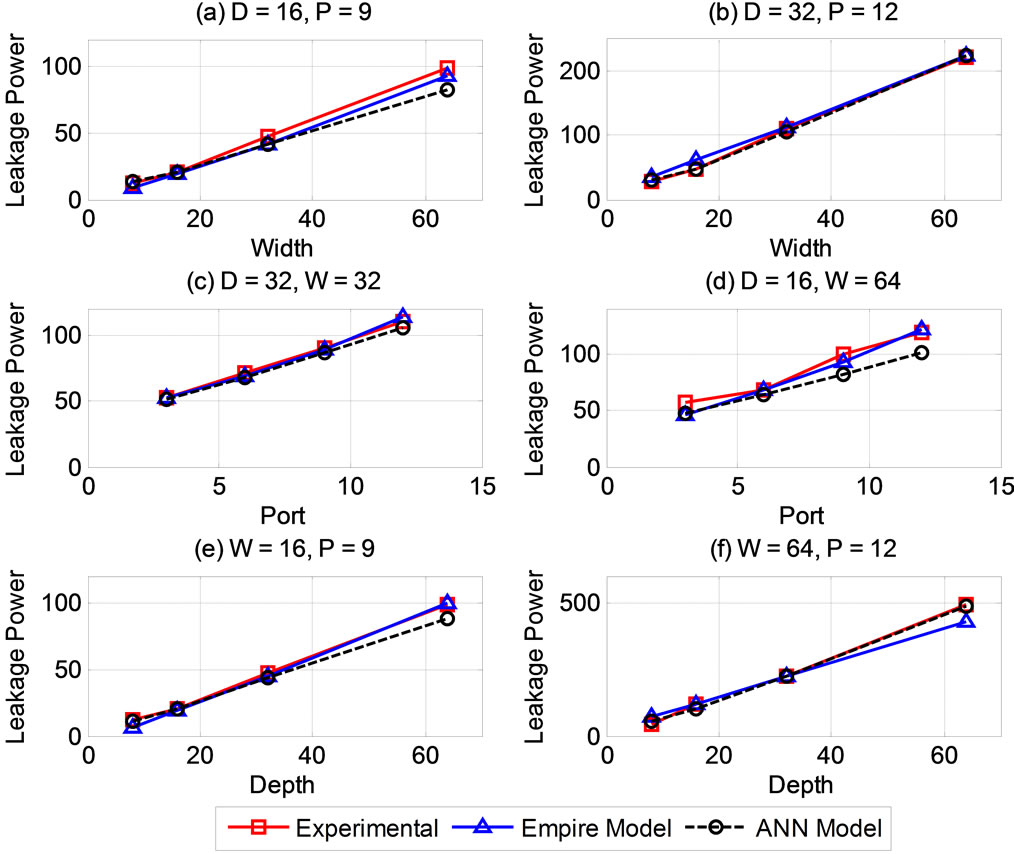
Figure 5. Comparison of leakage power for selected register files.
models for the tested instances was comparable with the ANN model underestimating in three instances (Figures 5(a), 5(d) and 5(e)). Although Empire performance seem to be better in these instances, however, for 20 randomly selected test cases, the overall performance of ANN model was better in as demonstrated by the several performance criteria shown in Table 3.
From the aforementioned analysis of results and validation of the ANN model, it is evident that the proposed ANN model can be used to provide designers with representative estimates of the energy/access and the leakage power of a perceived register file design before committing to silicon. The energy/access and the leakage power are shown in Figures 6 and 7 for all the register file designs used in this study assuming 130 nm technology and a supply voltage of 1.2 V.
6. Conclusions
Register Files are becoming a major source of power dissipation in processor cores impacting the limited energy budget provided by batteries in portable devices. It is impractical to delay design decisions that impact the power consumption of a processor till the back-end design phase. It is becoming imperative that designers should be able to explore architectural tradeoffs at an early stage of the design cycle.
In this paper, we proposed a novel neural network model for estimating energy and leakage power in register files. The model is simple and efficient and can be used to provide estimates that are close to those expected when detailed and time consuming simulation is performed. The model is validated by comparing its results
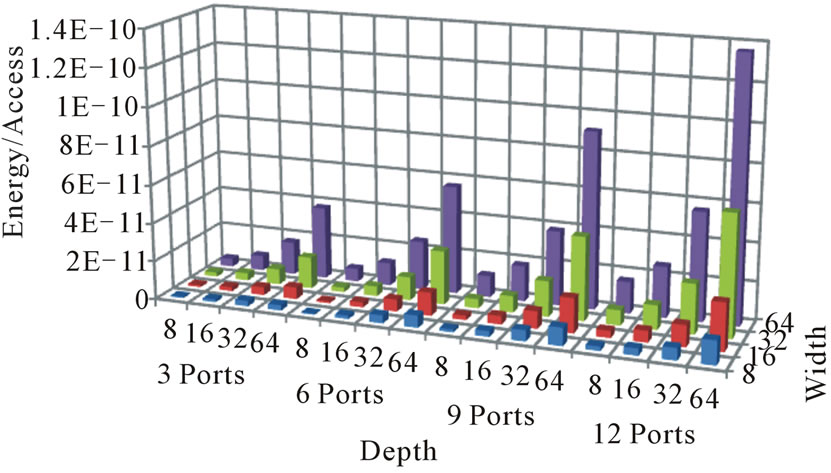
Figure 6. ANN model energy/access for all ports.
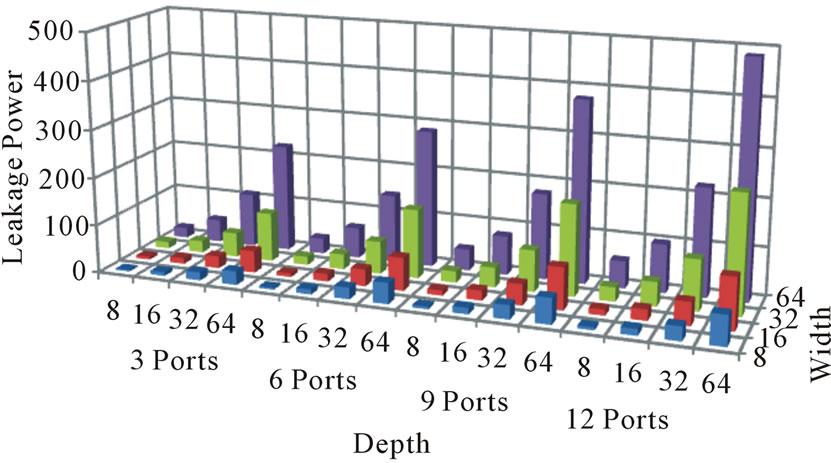
Figure 7. ANN model leakage power for all ports.
to those produced by low level simulation, as well as by comparing it to the recently reported Empire model [10].
7. Acknowledgements
The authors would like to thank Dr. Praveen Raghavan of IMEC in Belgium for providing the register file designs data for the 130 nm technology node.
REFERENCES
- N. Sung and T. Mudge, “The Micorarchitecure of a Low Power Register File,” Proceedings of the International Symposium on Low Power Electronics and Design, Seoul, 25-27 August 2003, pp. 384-389.
- X. Guan and Y. Fei, “Reducing Power Consumption of Embedded Processors through File Partitioning and Compiler Support,” Proceedings of the Conference on Application-Specific Systems, Architecture and Processors, Leuven, 2-4 July 2008, pp. 269-274.
- Y. Zhou, H. Guo and J. Gu, “Register File Customization for Low Power Embedded Processors,” IEEE International Conference on Computer Science and Information Technology, Beijing, 8-11 August 2009, pp. 92-96. doi:10.1109/ICCSIT.2009.5234988
- M. Kondo and H. Nakamura, “A Small, Fast and LowPower Register File by Bit-Partitioning,” 11th International Symposium on High-Performance Computer Architecture, San Francisco, 12-16 February 2005, pp. 40- 49. doi:10.1109/HPCA.2005.3
- M. Mueller et al., “Low Power Register File Architecture for Application Specific DSPs,” IEEE International Symposium on Circuits and Systems, 2002, Vol. 4, pp. 89-92.
- S. Wang, H. Yang, J. Hu and S. G. Ziavras, “Asymmetrically Banked Value-Aware Register Files for Low-Energy and High-Performance,” Microprocessors and Microsystems, Vol. 32, No. 3, 2008, pp. 171-182. doi:10.1016/j.micpro.2007.10.004
- H. Takamura, K. Inoue and V. G. Moshnyaga, “Reducing Access Count to Register Files through Operand Reuse,” Advances in Computer Architecture, Lecture Notes in Computer Science, Vol. 2823, 2003, pp. 112-121. doi:10.1007/978-3-540-39864-6_10
- W.-Y. Shieh and H.-D. Chen, “Saving Register-File Static Power by Monitoring Instruction Sequence in ROB,” Journal of Systems Architecture, Vol. 57, No. 4, 2011, pp. 327-339. doi:10.1016/j.sysarc.2011.02.004
- J. H. Tseng and K. Asanovic, “Energy-Efficient Register Access,” 13th Symposium on Integrated Circuits and System Design, Manaus, 18 September 2000, pp. 377-382.
- P. Raghavan, A. Lambrechts, M. Jayapala, F. Catthoor and D. Verkest, “EMPIRE: Empirical Power/Area/Timing Models for Register Files,” Microprocessors and Microsystems, Vol. 33, No. 4, 2009, pp. 295-300. doi:10.1016/j.micpro.2009.02.009
- D. Brooks, V. Tiwari and M. Martonosi, “Wattch: A Framework for Architectural-Level Power Analysis and Optimizations,” Proceedings of the 27th International Symposium on Computer Architecture, Vancouver, 14 June 2000, pp. 83-94.
- N. Kahraman and T. Yildirim, “Technology Independent Circuit Sizing for Standard Cell Based Design Using Neural Etworks,” Digital Signal Processing, Vol. 19, No. 4, 2009, pp. 708-714. doi:10.1016/j.dsp.2008.11.009
- F. Djeffal, M. Chahdi, A. Benhaya and M. L. Hafiane, “An Approach Based on Neural Computation to Simulate the Nano-Scale CMOS Circuits: Application to the Simulation of CMOS Inverter,” Solid-State Electronics, Vol. 51, No. 1, 2007, pp. 48-56. doi:10.1016/j.sse.2006.12.004
- P. Kalpana and K. Gunavathi, “Wavelet Based Fault Detection in Analog VLSI Circuits Using Neural Networks,” Applied Soft Computing, Vol. 8, No. 4, 2008, pp. 1592- 1598. doi:10.1016/j.asoc.2007.10.023
- A. Suissa, O. Romain, J. Denoulet, K. Hachicha and P. Garda, “Empirical Method Based on Neural Networks for Analog Power Modeling,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, Vol. 29, No. 5, 2010, pp. 839-844. doi:10.1109/TCAD.2010.2043759
- D. Dhabak and S. Pandit, “An Artificial Neural Network-Based Approach for Performance Modeling of Nano-Scale CMOS Inverter,” Institute of Engineering and Management Conference, January 2011, pp. 165-170.
- S. Haykin, “Neural Networks: A Comprehensive Foundation,” 2nd Edition, Prentice-Hall, Upper Saddle River, 1999.
- J. A. Abdalla and R. Hawileh, “Modeling and Simulation of Low-Cycle Fatigue Life of Steel Reinforcing Bars Using Artificial Neural Network,” Journal of the Franklin Institute, Vol. 348, No. 7, 2011, pp. 1393-1403. doi:10.1016/j.jfranklin.2010.04.005

