Journal of Modern Physics
Vol.09 No.06(2018), Article ID:84481,26 pages
10.4236/jmp.2018.96070
Can Really Regularized Amplitudes Be Obtained as Consistent with Their Expected Symmetry Properties?
Orimar Antônio Battistel1, Gilson Dallabona2, Marcus Vinicios Fonseca3, Luciana Ebani2,4
1Departamento de Física, Universidade Federal de Santa Maria, Santa Maria, Brazil
2Departamento de Física, Universidade Federal de Lavras, Lavras, Brazil
3Instituto Federal Farroupilha, São Vicente do Sul, Brazil
4Centro Brasileiro de Pesquisas Física, Rio de Janeiro, Brazil
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 26, 2018; Accepted: May 11, 2018; Published: May 14, 2018
ABSTRACT
Through a very detailed investigation involving a set of simple perturbative amplitudes we show that the answer for the question put in the title of the present work is: undoubtedly NO! We are not restricting the sentence to the amplitudes which are considered as anomalous. The referred investigation is performed by using a procedure alternative to the traditional regularization methods. In the context of such a strategy the amplitudes are not modified in intermediary steps of the calculation, like traditional regularization procedures do, and only the validity of the linearity in the integration operation is assumed in the operations made in Feynman integrals typical of the perturbative calculations. The central point of the investigation is the question related to the consistent interpretation of the amplitudes. For these purposes, in all amplitudes having power counting indicating the possibility of divergences, the relations among Green functions, Ward identities and low energy limits are analyzed, in a model having different species of massive spin fermions coupled to spin 0 and 1 (even and odd parity) boson fields, formulated in a space-time dimension . We show that the maintenance of the linearity in operations involving Feynman integrals excludes the possibility of an anomalous term in the Ward identity relating the axial-vector and the pseudo-scalar-vector two point functions amplitudes. In addition, we show that it is not possible the maintenance of Ward identities and low energy limits in a consistent way if the amplitudes of the perturbative calculations are quantities to be regularized, just because there is no regularization method which is capable to give acceptable results for the divergent objects present in the calculations. This conclusion includes the Dimensional Regularization method which cannot give unique results if the linearity and the symmetric integration are simultaneously required in Feynman integrals. The qualitative conclusions apply in an equally-way in other space-time dimensions having, therefore, implications in many phenomenological consequences of quantum field theories stated through perturbative solutions.
Keywords:
Perturbative Calculations, Anomalies, Ward Identities, Consistency

1. Introduction
It remains no doubt about the fact that the quantum field theory represents the adequate tool for the description of relativistic interactions of fundamental particles. The quantitative results obtained, mainly in scope of quantum electrodynamics, and the qualitative accordance between experimental data and theoretical predictions, within the context of the standard model, leave no room for hesitations in to agree with the preceding sentence, specially after the recent experiments in the large hadron collider where the Higgs Bosons discovery was announced. The construction of such a formalism is a consequence of a very hard work of many peoples along many years in searching for adequate interpretations for the perturbative solutions of quantum field theory, in particular for the quantum electrodynamics. This is due to the fact that in such type of solutions the amplitudes corresponding to basic processes are plagued by infinities or divergences so that an adequate interpretation is required in order to state the physical implications. Such an interpretation is given by the renormalization which, due to this reason, has played the role of a guide for the construction of theories having physical meaning. In this conceptual point of view, the theories are required to be renormalizable to get physical significance. The renormalizability, on the other hand, is deeply related to the maintenance, in the perturbative solutions, of the symmetries implemented in the construction of the theory. At first sight it seems obvious that the solutions will reflect the symmetries of the theory. However, as it is well known, within the context of quantum field theory obvious expectations are not always materialized. We are referring to the most intriguing and subtle aspect of quantum field theory; the unavoidable violations of symmetry relations or anomalies [1] - [8] . Since the violations are unavoidable, the theories having anomalies are not renormalizable. The renormalization is only possible if different species of fermions are present at the theory so that anomalies coming from different sectors produce an exact cancellation, which is the anomaly cancellation mechanism, a fundamental ingredient of the standard model responsible for the presence of six quarks and six leptons in the theory. The anomalies eliminated in the standard model are those associated to the single (AVV) and triple (AAA) axial vector triangles. For these amplitudes it can be shown that four general expectations based on symmetries can be stated: three Ward identities and one low-energy limit. However, through very general arguments, not restricted to perturbative solutions, it can be shown that it is not possible to obtain a mathematical expression possessing simultaneously all four symmetry properties. In order to verify this fact, in an explicit way, only the perturbative calculation is possible. But this is not a trivial task since the corresponding amplitudes, one-loop triangles, are divergent quantities corresponding to a linear divergence degree. The linear divergence implies that the amplitude is not invariant under a shift in the loop momentum which means that the result may be dependent on the choices made for the routing of the internal lines. The divergence character requires, on the other hand, the adoption of some prescription to handle the problem, which means to regularize the amplitudes in a first step in order to allow the necessary manipulations and calculations. The result within this context may be also dependent on the specific regularization prescription adopted. The dimensional regularization [9] [10] [11] , strictly speaking, cannot be applied since odd tensors (the Levi-Civita tensor) do not admit extensions to continuum and complex dimensions. Due to this reason the discussions about explicit (perturbative) calculations of the triangle anomalies are made in a scenario where the amplitudes are admitted to be ambiguous quantities and the violations in symmetry relations are associated to their divergent character [4] : it is not possible to choose the arbitrariness involved such that the four expected symmetry properties can be satisfied [12] [13] [14] . Guided by phenomenological reasons, in the AVV triangle, the low-energy limit is preserved and, as a consequence, the vector currents involved are assumed preserved while the axial vector current is assumed violated.
Some of the arguments adopted in the perturbative description of anomalies have been recently put in doubt since it was demonstrated that the divergent amplitudes are not the unique anomalous amplitudes [15] . The referred investigations allow to conjecture that the divergent anomalous amplitudes, in each even space-time dimension, are only the simplest structures. They are related to a chain of finite anomalous amplitudes such that the association of divergences and ambiguities to anomalies seem not to be correct.
The aspects related to the regularization of perturbative amplitudes still remain as an important theme in quantum field theory. In a recent work [16] , made by many hands, a detailed discussion about the questions relative to the regularization process, within the context of the most representative methods, including the one adopted in the present work, have been made. Such a work can be considered as an important support to the argument that the interpretation of the perturbative amplitudes requires additional investigations. If one agrees with this point of view, the present work may represents an useful contribution.
In the present work we add new and, perhaps, surprising facts related to the consistent interpretation of perturbative amplitudes. We show, through a careful and detailed investigation, that the phenomenon of unavoidable violation in symmetry relations is not restricted to that admitted as anomalous. Following rigorously the same steps used to state the anomalies, which means to state the most general form for the involved tensor, imposing the Ward identities and stating the low-energy limits, it is possible to show that an expression consistent with the Ward identities and low-energy limits involved cannot be obtained, within the context of regularizations, in a completely similar way as it is observed in the case of anomalous amplitudes. In order to appreciate these facts we consider the general case where different specie of massive fermions are coupled to boson fields (scalar, pseudoscalar, vector and axial-vector). In this model, the vector current is precisely related to the scalar current in a similar way as the axial is related to the pseudoscalar one allowing general, clear and transparent conclusions. The space-time dimension is chosen in order to avoid unnecessary algebraic difficulties involved in higher dimensions but the main aspects can be stated in other space-time dimensions in a completely similar way. The conclusions seem to indicate that another interpretation for the perturbative amplitudes is required since, in a clear way, the usual interpretation given for these mathematical structures, as regularized quantities, cannot produce consistent results, in a way independent of the specific regularization adopted.
The work is organized as follows. In Section 2 we define the model, notation and the one and two-points Green functions. In Section 3 we use these definitions, in addition to the Dirac matrices properties, to establish a set of relations among the involved Green functions. The general form for the tensors are used to state low-energy limits to the correspondent Green functions in the Section 4. The method to deal with divergent amplitudes is described in Section 5 and in the Section 6 we explicitly calculate the one and two-point functions by following the method described in Section 5. The Section 7 is dedicated to explicitly verify the relations among Green functions established in Section 3 using the results from Section 6. Divergent objects on the amplitudes, low-energy limits are detailed, respectively, in the Sections 8 and 9. A general discussion about all presented results is performed in the Section 10.
2. The Model
In order to state the elements for the present investigation let us consider the following interaction Lagrangian
(1)
where, is a spin massive field which is coupled to the bosonic: scalar , pseudoscalar , vector and axial-vector fields. The indexes a, b and c are relative to the different flavors and , , and are operators connecting different species of bosons and fermions of the theory. The factors , , , and are coupling constants while are matrices constituting a two dimensional representation of the Dirac algebra and, finally, is the two-dimensional matrix responsible for the odd parity behavior of the pseudoscalar and axial-vector fermionic currents. The referred fermionic currents are identified as
where the operators , according to the interaction Lagrangian, can be , , and characterizing the densities: scalar , pseudoscalar , vector and axial-vector , respectively. They are related through
(2)
(3)
which implies in Ward identities for the perturbative amplitudes.
For our present purposes it is enough to define the one-loop fermionic two-point functions
for one value of the loop momentum, where
is the fermionic propagator. The expression for the quantities can be also written in the form,
The one-loop amplitudes are obtained from the above quantities after implementing the last Feynman rule, which means to integrate over the loop momentum
At this point it is convenient to define also the one-point structures
The corresponding one-loop amplitudes are then given by
(4)
They are related to the two-point ones through relations among Green functions, as we will see in a moment. We, intentionally, separated the implementation of the last Feynman rule from the other ones as a part of the procedure we will adopt to manipulate and calculate the divergences of the perturbative calculations.
3. Statement of Relations among Green Functions
By using the definitions of the one and two-point functions structures, in addition to the Dirac matrices properties, it is possible to state relations among these quantities every time we have a Lorentz index, by contracting the amplitudes with the external momentum. For one contraction we have
(5)
(6)
(7)
(8)
(9)
(10)
(11)
and, for two contractions,
(12)
(13)
(14)
Such relations can be converted into relations among the one-loop Green functions after the integration over the loop momentum k, on both sides. This means that after calculating the one and two-point functions we have to get these relations satisfied as a consequence of the linearity of the trace and integration operations.
4. General Form for the Tensors and Low-Energy Limits
It is possible to obtain important properties for the amplitudes by combining their general tensor structures with their symmetry relations or Ward identities. These results are not restricted to the perturbative solutions and must remain valid even for exact solutions.
A. Vector indexes
Let us start by the ones having one Lorentz index. The SV function is a vector constructed with the external vector 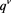 so that we have to get a general form
so that we have to get a general form
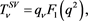
where  is an invariant function of the external momentum. The general form allows us to state a low-energy prediction for this amplitude. First
is an invariant function of the external momentum. The general form allows us to state a low-energy prediction for this amplitude. First

and then it is expected that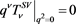 , since
, since  may not have a pole at
may not have a pole at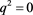 . However, the proportionality between the vector current with the scalar one, Equation (2), states that
. However, the proportionality between the vector current with the scalar one, Equation (2), states that
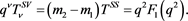
This implies that it is also expected that , as a consequence of the Ward identity relating the vector and the scalar fermionic currents.
, as a consequence of the Ward identity relating the vector and the scalar fermionic currents.
Now we consider the VV function. The expected general form can be written in a very convenient way

Contracting with the external momenta
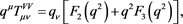
and using the Ward identity , we get
, we get
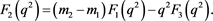 (15)
(15)
Here we can identify a low-energy limit given by

Then it is expected that the  term in the VV function satisfies
term in the VV function satisfies
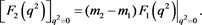
A very interesting aspect, however, is relative to the second contraction
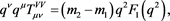
which implies that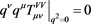 . In this way the two-point functions SS, VS and VV as well as the one-point ones S and V are involved in these low-energy predictions.
. In this way the two-point functions SS, VS and VV as well as the one-point ones S and V are involved in these low-energy predictions.
B. Axial indexes
Now let us consider the AP function. The general form is similar to that of SV function
such that
where 



which implies that
Now we consider the AA function. Similarly to VV amplitude we have
The Ward identities allow us the identification
As a consequence we have
Again we can identify a low-energy implication
Now we can see that the two contractions lead to
which implies that we have to get
C. Axial and vector indexes
Now let us consider the functions having an odd number of

The tensor 

and it is expected that
A low-energy implication follows
Contracting now the amplitude with the axial vertex momentum, we obtain
and, as a consequence,
or yet
Now since
we have
This expression means that at 
or in another way
This is the implication analogous to the equal mass case, which is

At this point, the relevant question is: can we evaluate all the involved perturbative amplitudes so that the expected properties, relations among Green functions, Ward identities and low-energy limits can be satisfied simultaneously? This is our challenge since there are mathematical troubles in the amplitude definitions which must be consistently handled in order to find adequate solutions for the perturbative amplitudes.
5. The Strategy to Handle the Divergences of the Perturbative Calculation
In the preceding sections we have introduced a general interaction Lagrangian and constructed the one-loop amplitudes through the ingredients given by the Feynman rules, for one value of the loop momentum, which may become divergent after integration over all such values. The integration was not taken precisely by the fact that some amplitudes, in that case, will become mathematically undefined quantities and the posterior operations are dangerous since all the physical content of the amplitudes (external momentum dependence) will be present in divergent integrals and then the calculations only become possible if some modifications of the amplitudes are made. Schematically, we have to adopt the following procedure

where the


In order to avoid the problems related with the usual regularization schemes we will adopt an alternative procedure to perform all the necessary calculations in the perturbative amplitudes, including renormalization processes, without modifying the amplitudes as they emerge from the Feynman rules. The procedure is in addition universal in the sense that any amplitude of any theory in any space-time dimension is treated in the same way. Such strategy, proposed and developed by O. A. Battistel originally in Ref. [17] , is founded in a simple idea: to avoid the critical step involved in the regularization process which is the explicit evaluation of divergent integrals.
The implementation of the procedure is simple. The central idea is to write the propagators in a way that the momentum structure is emphasized. The divergences occur because the conditions imposed in the differential equation for the Green functions of the free part are not enough to render the perturbative solutions of the interacting theory convergent. More restrictive convergence conditions would be necessary. So it is possible to separate the part of the propagators which are responsible for the divergences if a decreasing power series is generated. Schematically, we can represent the summation as
where the corresponding integrals have a power counting which decreases as n increases, such that the last term can be convergent. If this is possible then the connection limit can be taken in such term which means to remove the distribution from the integral just because the integration and the limit commute in this case, such that the right hand side can be written as
In this step, it is assumed only the validity of the linearity in the integration process. The last integral can be performed without specifying the regulating distribution and the result must be universal (regularization independent).
According to the space-time dimension more inverse power will be associated to divergences but there always will be a certain power which will correspond to convergent terms. This scenario will be perfect if no physical parameter are present in the potentially divergent terms such that the part which contains the energy-momentum dependence will reside totally in the convergent term. The remaining potentially divergent terms will be, in principle, dependent on the specific regularization. However, there will be properties of them which may be universal too, as we will see in a moment.
In order to implement such procedure we can adopt an adequate representation for a propagator carrying momentum 

Note that, as N increases, the convergence becomes better. This identity is very convenient for our purposes. Here 

The tensorial structure states general properties for such objects. Among such properties, there must be a relation among them such that all the objects above can be reduced to first one. These relations must be independent of the particular regularization.
The set of potentially divergent terms can be then separated in two classes of objects; the irreducible ones and those which are convenient combinations of terms having the same degree of divergences but different tensorial structures. Such objects are not really integrated as we will show in a moment, so that no divergent integrals need in fact to be solved. In renormalizable theories the irreducible objects can be absorbed in the reparametrization of the theory and in nonrenormalizable models they will be directly adjusted to phenomenological parameters in the parametrization of the model, in each specific level of approximation considered. More details about these aspect of the procedure will be presented in a moment when the chosen amplitude is evaluated.
In order to make clear the point stated above, as an example, for the present case the fermion propagator can be written as

This expression is obtained by taking 

By using the above form for the fermionic propagator we will have the desirable property for all one-loop amplitudes in which all the dependence on the internal momenta will be in present in finite integrals. However, unnecessary algebraic efforts can be avoided noting that in cases of lower than N divergence degree we can (before or after taken the integration) turn back one or more steps in the above expansion of the propagator until the dependence on the internal momenta is located in finite integrals. This point will become clear in what follows. Let us now evaluate the one-loop amplitudes involved in our investigation within the context of the above described procedure and then show many other aspects of the referred strategy.
6. Explicit Calculations of One and Two-Point Functions
We start, following the strategy described in the preceding section, by considering the evaluation of the simplest ones but those having the higher divergence degree in the theory which is the one-point scalar, vector and axial fermionic Green functions defined in (4). Let us consider one of them in details, in order to illustrate the procedure. We first write

where

or, since the odd terms will be ruled out after the integration, we write

For the second term the same expression for the propagator can be used. However, in order to avoid unnecessary algebraic efforts we can note that it is equivalent to adopt the expression (18) corresponding to

Adding the two terms, (21) and (22), in order to obtain the vector Green function,
so that the dependence on the arbitrary internal momentum is located in finite integrals. The divergent terms will not contain physical quantities since λ is an arbitrary parameter which will play the role of a common scale for the divergent and finite parts. We can then introduce the integration on both sides in order to obtain the physical amplitude. It is certainly correct to say that
The integration of the (finite) integrals obtained reveals an exact cancellation. This means that we can state the formal relation

where we have defined

With the same ingredients we get

Note the completely arbitrary character of the results. Analogously, for the S function we can state that

The integration of the (finite) integral obtained reveals that the formal relation can be stated

with
The function 
Following the same procedure, in the same spirit adopted above, we get the following results for the two-point functions









where we introduced the functions
In the above expressions (and in future ones), the arguments of such functions are omitted by simplicity.
At this point it is interesting to note that the mathematical forms of the amplitudes presented above preserve all the arbitrariness involved in this type of calculations. In addition, no modification, relative to the implication of Feynman rules, has been introduced, as is usual in regularization prescriptions. On the other hand, since only finite integrals have been solved, the results corresponding to particular regularizations can be obtained directly from the above expressions. For this purposes it is only necessary to perform the integration of the two divergent objects present in the expressions; 

7. Verification of Relation among Green Functions
Before any analyses we have to verify the consistency of the performed operation. We must test the obtained results concerning the maintenance of the linearity in the integration operation. In our problem, a crucial test is the verification of the relations among Green function stated in the section III. We start by the VV function, Equation (34). Contracting with external momentum
The second term can be identified as
so that we have obtained,
which is in accordance with the expectation stated by the expression (5).
For the SV function, Equation (30), we first state
Using the relation between finite functions
which reduces the function 

we write
which is the desired result stated through the expression (6), given the expressions (27) and (28) to S and SS amplitudes.
Contracting the expression for the AA amplitude, Equation (35) we get
which implies that
by comparing with the expression (23) and (33) to the functions V and PA.
By contracting the obtained expression, Equation (33), we get
Again we reduce the function 

The contraction
By contracting the expression (36) with the external momentum we get
Comparing with the expression (31) and (25) for the AS and A functions, we conclude that
which means that the relation is preserved. Now we contract with the axial index,

Using the relation among the finite functions
we obtain
Now looking at the expression above, in order to identify the involved one-point A functions, Equation (25), it is first necessary to use a 2D version of the Schouten identity
It is easy then to identify the one and two-point amplitudes such that
Differently from the preceding cases, here the expected relation is only obtained if the condition 
This is a difference between two logarithmically divergent structures. However, using, one more time, the linearity of the integration operation, we can add and subtract 
Note that this quantity represents the trace of the object
8. Ward Identities and Divergent Object
In the preceding section we verified if the relations established to perturbative 1-loop amplitudes have been preserved by the performed operations in the context of adopted strategy. All relations among Green functions are preserved without any condition for the value of the divergent quantities present at the expressions for the amplitudes within the context of the adopted mathematical language, except the one corresponding to the contraction of the AV amplitude with the external momentum with the axial index. This means that all regularizations are capable to fulfill such relations independent of the value attributed to the divergent objects, except that for the axial index of the AV amplitude where a specific (but reasonable) property is required. This exception character is obviously related to the axial anomaly, as we will discuss in what follows.
At this point we must consider the crucial question in perturbative calculations: are the results consistent with the symmetry content of the model? In this case this means to satisfy the Ward identities. The problem is simple in the sense that we have at our disposal only two unspecified quantities; 

Let us start by the amplitudes having two Lorentz indexes. The relation (5)
reveals in a very transparent way that the Ward identity corresponding to the divergent of the vector current will be satisfied only if the two first term on the right hand side are absent. Following the usual interpretation, the amplitudes require a regularization. So the question is: Is there a regularization which is capable to do the one-point V function identically zero? Looking at the expression
we see that apparently two options are possible. The first is to choose the arbitrary internal momentum 



This is possible within the context of dimensional regularization, for example. So, without questioning if this is consistent, for a while, we accept this condition as a Consistency Relation (CR), just because it seems that we do not have another option at this point. As a consequence the required Ward identities
are preserved. The same analysis for the AA amplitude leads us to the same conclusion. In this case the reason is obviously related to the fact that with the CR assumption
Now we take the AV function, given by (after assuming the CR),
and then
Now we consider the axial vector index. It is immediate to see that
showing that the axial-vector Ward identity is violated due to the presence of the nonambiguous finite term





there are only two possibilities: both objects 


where 

It is easy to accept that this is equal to
Then, we introduce the last Feynman rule. The integration of the two imediately above quantities must be identified as being equivalents, due to the linear character of the integration operation. So, it seems that the zero value attributed to the object 

Looking at the relations among Green functions
it is simple to see that there is only one condition which is capable to guarantee the preservation of Ward identities which is the identically zero value for the S one-point functions. This means that it is required that
for any fair procedures. This is not the complete history. Let us next analyze the low-energy limits.
9. Low-Energy Limits
In the section IV we obtained low-energy predictions for the amplitudes stated as a consequence of Ward identities and the general tensorial aspects of the amplitudes. In the previous section we concluded that it is not possible to fulfill the conditions required in order to obtain all amplitudes satisfying their Ward identities. In this section we will complete our investigation by making an additional exercise. Let us accept that the required conditions are satisfied in a hypothetical way, and verify the predicted low-energy limits. This exercise is necessary just because, otherwise, the verification of low-energy limit is immaterial, since such results have been obtained by assuming the validity of the symmetry relations. Let us, in a first moment, assume that a regularization, which is capable to obtain
does exist (without believing that this is really possible). The 



We start by considering the SV amplitude. The obtained result is
revealing that the expect property 
obtained by simply removing the quantities 
and, therefore, 
The same occurs with the AP and PP relation. While the low-energy limit for AP function is naturally preserved, the prediction for the PP function will be not fulfilled, since even if the Ward identity violating terms are removed “by hand” we will get
Finally, let us consider the amplitudes which are odd tensors. The low-energy limit
is predicted to be zero. Therefore, it is not preserved as well as in the case of SV and AP.
The violation involved in the above considered limit is expected, just because it is precisely the one related to the AV axial anomaly problem. However, it is important to note that, at the same scenario, we have other violations in the predicted low energy limits, which are usually not expected. Due to this reason, the immediately above considered case do not have a status of exception. If all the amplitudes are treated in the same way, the violation in the predicted low energy behaviour, is the rule and not an exception. The conclusion is transparent: the interpretation given for the perturbative amplitudes as quantities to be regularized cannot give us consistent results in a wide sense.
10. Final Remarks and Conclusions
Quantum Field theory has obtained very important successes in the accordance between theoretical predictions and experimental data. Such successes have been obtained through perturbative solutions where the amplitudes are taken as quantities to be regularized and after renormalized. Due to this reason only renormalizable quantum field theory are part of the referred successes. It is a fact. However, there are very intriguing aspects in the adopted procedures, relative to the interpretation of the perturbative amplitudes as regularized quantities. In the present work we developed a detailed investigation in order to show some of such aspects. The dimension adopted for the space-time is just to give us the simplest scenario from the mathematical point of view, but the points discussed here are present in all space-time dimensions in all theories and models. The authors of the present work have been made a considerable effort in order to understand in the deepest way the questions relative to the consistency in perturbative calculations. Part of such efforts resulted in a simple and transparent procedure to make the required manipulations and calculations where it is possible to avoid the use of regularizations in intermediary steps as well as a complete systematization of the procedures has been obtained. After this it is simple to identify some situations where it is apparently not possible to obtain the required consistency. The simple investigation presented here exhibits some of such situations. The required calculations are very simple. In spite of this, the conclusions are powerful.
The main point of our work is the requirement of the validity of the linearity in integration operation in Feynman integrals, in spite of the divergent character involved, at any stage of the calculations. It seems so simple and obvious to require the preservation of this absolutely fundamental mathematical property in the operations made in perturbative calculations of quantum field theory, but this is a difficulty for all regularization procedures, specially for the dimensional regularization. It is not usual to emphasize this aspect just because it is not usual to verify if the obtained results are consistent with such requirement. Given the presence of mathematical indefinitions at the loop amplitudes, the preservation of the linearity in the manipulations made in Feynman integrals is not automatic. Because of this, such property can be used as a powerful constrain in the searching for the consistent interpretation of the perturbative amplitudes. It is certainly a very difficult situation to state physical consequences of a theory through the solutions which breaks the linearity in the integration operation. A simple but important consequence is that it is possible to show that all anomalous terms are linearity breaking, as we have shown in the considered case. In a consistent calculation, such terms cannot be present. It is possible to identify, in a very clear way, the step where the anomalous term emerge, just because it is precisely where the referred linearity is broken. In the expression for the AV amplitude, Equation (37), we have the term
and then two terms appeared. The first term, in the right hand side, will generate two one-point axial amplitudes while the second one will add to the term




The correct procedure, given such analyses, is to obtain a nonzero value for the object 

for, in a second step, violate also the linearity. Explicitly, we have
The same result can be obtained in the presence of any regulating function. The result within the context of dimensional regularization can be understood if we rewrite the above object in a different way
It is a surface term and so is taken as zero in dimensional regularization, by construction. But this assumption is clearly not compatible with symmetric integration and linearity, as shown above. In addition, this make possible that the trace can be obtained as nonzero for an identically zero tensor. On the other hand, it is very simple to verify that
for any 

just because, the preservation of these symmetry relations requires that
This would be a completely absurd idea. In dimensional regularization we have a nonzero value and a pole in the value


The low-energy limits analysis reveals an additional aspect. Even if the Ward identities are preserved by assuming the contradictory results, 


The conclusion is clear: it is not possible to give a consistent interpretation for the perturbative amplitudes as regularized quantities. In other words, do not exists a (honest or not) regularization procedure which is capable to leads to the expected (consistent) results.
All the conclusions stated here are constructed as a consequence of the application of a very careful procedure, which is, in addition, very simple in such a way that all the results presented here can be easily checked. The implications, however, seem to be very important since many phenomenological implications are linked to these fine tuning aspects of the perturbative calculations in quantum field theory. Many controversies aroused in recent years are deeply related to the questions discussed here.
Finally, at this point, it is unavoidable to formulate the question: Can we believe that it is possible to construct an adequate interpretation for the perturbative amplitudes without considering them as quantities to be regularized? The answer seems to be: yes. A work following this line of reasoning is presently in preparation.
Acknowledgements
L. Ebani acknowledge a grant from CNPq/Brazil.
Cite this paper
Battistel, O.A., Dallabona, G., Fonseca, M.V. and Ebani, L. (2018) Can Really Regularized Amplitudes Be Obtained as Consistent with Their Expected Symmetry Properties? Journal of Modern Physics, 9, 1153-1178. https://doi.org/10.4236/jmp.2018.96070
References
- 1. Adler, S. (1969) Physical Review, 177, 2426-2438. https://doi.org/10.1103/PhysRev.177.2426
- 2. Bardeen, W.A. (1969) Physical Review, 184, 1848-1857. https://doi.org/10.1103/PhysRev.184.1848
- 3. Bell, J.S. and Jackiw, R. (1969) Nuovo Cimento A, 60, 47-61. https://doi.org/10.1007/BF02823296
- 4. Jackiw, R. (2000) International Journal of Modern Physics B, 14, 2011-2022. https://doi.org/10.1142/S021797920000114X
- 5. Treiman, S.B., Jackiw, R., Zumino, B. and Witten, E. (1985) Current Algebra and Anomalies. World Scientific, Singapore. https://doi.org/10.1142/0131
- 6. Gross, D. and Jackiw, R. (1972) Physical Review D, 6, 477-493. https://doi.org/10.1103/PhysRevD.6.477
- 7. Gerstein, L.S. and Jackiw, R. (1969) Physical Review, 181, 1955-1963. https://doi.org/10.1103/PhysRev.181.1955
- 8. Bertlman, R.A. (1996) Anomalies in Quantum Field Theory. Clarendon Press, Oxford.
- 9. ’t Hooft, G. and Veltman, M. (1972) Nuclear Physics B, 44, 189-213. https://doi.org/10.1016/0550-3213(72)90279-9
- 10. Bollini, C.G. and Giambiagi, J.J. (1972) Physics Letters B, 40, 566-568. https://doi.org/10.1016/0370-2693(72)90483-2
- 11. Ashmore, J.F. (1972) Nuovo Cimento Letters, 4, 289-290. https://doi.org/10.1007/BF02824407
- 12. Sutherland, D.G. (1966) Physics Letters, 23, 384-385. https://doi.org/10.1016/0031-9163(66)90477-X
- 13. Sutherland, D.G. (1967) Nuclear Physics B, 2, 433-440. https://doi.org/10.1016/0550-3213(67)90180-0
- 14. Veltman, M. (1967) Procedure Royal Society A, 301, 107. https://doi.org/10.1098/rspa.1967.0193
- 15. Battistel, O.A., Fonseca, M.V.S. and Dallabona, G. (2012) Physical Review D, 85, 085007. https://doi.org/10.1103/PhysRevD.85.085007
- 16. Gnendiger, C., et al. (2017) European Physical Journal C, 77, 471. https://doi.org/10.1140/epjc/s10052-017-5023-2
- 17. Battistel, O.A. (1999) A New Strategy to Manipulate and Calculate Divergencies in TQC. PhD Thesis, Universidade Federal de Minas Gerais, Brazil.
- 18. Pauli, W. and Villars, F. (1949) Review Modern Physics, 21, 433. https://doi.org/10.1103/RevModPhys.21.434


















































































