Journal of Modern Physics
Vol.08 No.08(2017), Article ID:77233,7 pages
10.4236/jmp.2017.88073
On Excited Meson Spectra in the Scalar Strong Interaction Hadron Theory
F. C. Hoh
Retired, Dragarbrunnsg. 55C, 75320 Uppsala, Sweden

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 3, 2017; Accepted: June 25, 2017; Published: June 28, 2017
ABSTRACT
Meson spectra have been treated earlier in the scalar strong interaction hadron theory, choosing the Coulomb and linear type of potentials, neglecting the quadratic one. The spectra of ground state pseudoscalar and vector mesons were adequately accounted for but not that of the excited mesons. Here, the quadratic potential replaces the Coulomb one and the same ground state meson spectra were recovered. Also, the masses of low-lying radially excited pseudoscalar and vector mesons were found to be 4% - 18% smaller than the measured ones. Here, the linear type of potential, by itself of nonlinear nature, has been neglected. For some orbitally excited pseudoscalar mesons, the difference is 14% - 38%. The discrepancies are tentatively attributed to the neglected nonlinear potential, which is expected to increase with meson mass, as can be seen in the tables below.
Keywords:
Excited Meson Spectra, Quadratic Confinement, Scalar Strong Interaction

1. Introduction
The Schrödinger-Dirac equations became an established theory because of their ability to account for atomic spectra in the early stages of development. Similarly, any viable hadron theory must be able to account at least approximately for the meson spectra. Quantum Chromodynamics (QCD) (see e.g. [1] ), the main stream strong interaction theory, has failed to do this, after decades of work and lattice computations. Therefore, the low energy, nonperturbative end of QCD has to be abandoned.
On the other hand, the scalar strong interaction hadron theory (SSI) can approximately but adequately account for the masses of the ground state pseudoscalar mesons 0- (singlet) and vector mesons 1- (triplet) [2] [3] [4] . However, predictions of the spectra of the excited states of these mesons using the same linearized equations turned out to contradict data [5] ; the spacing between the energy levels according to (7) below turned out to be too small. The nonlinear strong interaction potential was called in to mitigate this difficulty phenomenologically ( [4] Section 5.5-7).
This difficulty is incompatible with a viable SSI. The purpose of this paper is to resolve it and provide predictions in rough agreement with data without the above phenomenology.
2. Background, Coulomb and Linear Type of Potential
In SSI, the interaction potential between the quark and the antiquark in a meson is given in ( [2] 7.2, [4] 3.2.8),
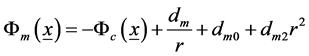 (1)
(1)
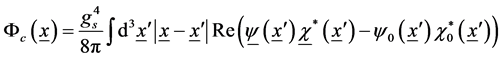 (2)
(2)
Here, 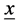 is the interquark distance vector and also denotes the “hidden” relative space,
is the interquark distance vector and also denotes the “hidden” relative space, 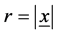 , the dm’s integration constants of the fourth order differential equation ( [2] 6.9, [4] 3.1.11), gs the strong interaction coupling constant, y0 (singlet) and
, the dm’s integration constants of the fourth order differential equation ( [2] 6.9, [4] 3.1.11), gs the strong interaction coupling constant, y0 (singlet) and 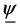 (triplet) the rest frame meson wave functions in
(triplet) the rest frame meson wave functions in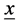 . In the case of zero orbital momentum, l = 0, these wave functions are determined by ( [4] 3.2.5b, 3.4.1, 3.4.2a, 3.4.3)
. In the case of zero orbital momentum, l = 0, these wave functions are determined by ( [4] 3.2.5b, 3.4.1, 3.4.2a, 3.4.3)
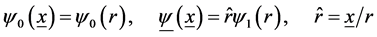 (3)
(3)
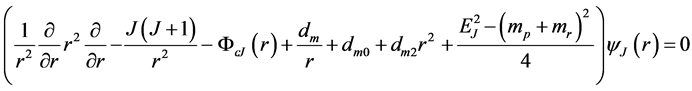 (4)
(4)
derived from ( [4] 3.2.10b, 3.2.11a). Here mp,r are quark masses of flavors p, r, J = 0 refers to singlet and J = 1 to triplet and (2) becomes ( [4] 3.2.17)
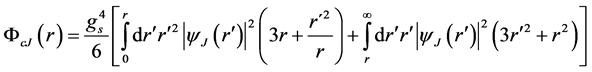 (5)
(5)
In early 1990’s, when the above work was in progress, potential models suggested a confinement potential of the Coulomb plus linear type ( [6] , [7] §14.3.2). The nonlinear ΦcJ leads to linear confinement at large r ( [2] 7.11b [4] 3.2.19). The Coulomb term dm/r was kept and the quadratic term dm2r2 dropped ( [4] 3.2.20). In this case, the linearized (4) with ΦcJ®0 is of the same form as that for the hydrogen atom and the ground state solutions are given by ( [4] 4.3.1-3)
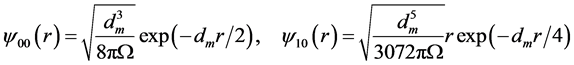 (6)
(6)
where the second subscript refers to radial quantum number nr = 0. These wave functions, being plane waves in the laboratory frame , vanish when the normalization volume Ω à ¥ ( [4] 4.7.2) so the above assumption ΦcJ ® 0 holds. The meson mass EJ0 is given by a slightly extended ( [4] 4.4.1)
, vanish when the normalization volume Ω à ¥ ( [4] 4.7.2) so the above assumption ΦcJ ® 0 holds. The meson mass EJ0 is given by a slightly extended ( [4] 4.4.1)
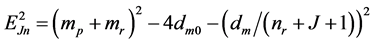 (7)
(7)
This result with nr = 0 and the empirical 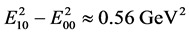 ( [4] 5.2.2) together with six pseudoscalar meson masses determine the five quark masses, dm, and dm0 ( [2] 10.2, [3] Table 1, [4] 5.2.3, Table 5.1). The results are summarized in Table 1 below.
( [4] 5.2.2) together with six pseudoscalar meson masses determine the five quark masses, dm, and dm0 ( [2] 10.2, [3] Table 1, [4] 5.2.3, Table 5.1). The results are summarized in Table 1 below.
Table 1 and (7) predict many other ground state pseudoscalar and vector meson masses with good approximation ( [3] , [4] 5.2.3, Tables 5.3-5).
However, for radially excited pseudoscalar and vector mesons, nr ³ 1 and (7) shows that the spacings between successive radially excited meson masses, analogous to those between excited states in a hydrogen atom, are too small and are decreasing rapidly with increasing nr, contrary to data ( [4] Tables 5.6-7). In an attempt to remove this discrepancy, an assumption ( [4] 4.7.5) was made in which the normalization volume Ω à Ωc is made finite in (6) for the excited states. The wave functions in the nonlinear ΦcJ in (5) now no longer vanish. Since ΦcJ is a positive quantity, it will increase the meson masses.
Not being able to treat this complex nonlinear problem, Φm(r) in (1) was replaced by unknown parameters ( [4] 5.5.2) which are determined by using data points, the masses of chosen excited mesons. In this way, the results in ( [4] Tables 5.6-7) were obtained, after having spent many data points.
Obviously, the above treatment failed to account for the spectra of excited mesons.
3. Quadratic Confinement
In reviewing the above treatment, it is seen that there is no compelling justification to drop dm2r2 in (1), (4), as was done below (5), except that the linearized (4) with ΦcJ = 0 turns out to have no converging solution. Therefore, put dm = 0 and keep the quadratic confining dm2r2 in (4). The solution analogous to (6) is of harmonic oscillator type and reads
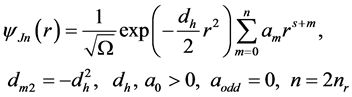 (8a)
(8a)
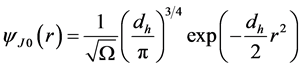 (8b)
(8b)
where Ω denotes the nomalization box in ( [4] 4.2.8) for the ground state (8b).
The series in (8a) terminates when
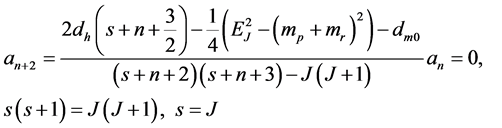 (9)
(9)
Table 1. Quarks masses and two integration constants in SSI obatined in [3, 2]. These are also reproduced in ( [4] 5.2.3 and Table 5.1).
Here, the other root 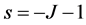 leads to divergent wave function at r = 0 and is dropped. Now, (7) is changed to
leads to divergent wave function at r = 0 and is dropped. Now, (7) is changed to

which differs from (7) only in the last term. The above ground state results for nr = 0 mentioned in Table 1 and the two lines below it can now be taken over if the last two columns in Table 1 are replaced by

4. Radially Excited Mesons
Comparison of (7) to (10) shows that the latter gives much larger spacings between the excited states. Application of (10) to the radially excited states in ( [4] Table 5.6, 5.7) are given in Table 2 and Table 3 below.
Table 2. Masses (MeV) of low-lying excited singlet l = 0 mesons considered in ( [4] Table 5.6). Data Eexp [5] are given in brackets [..]. Below these are the predicted masses Eth from (10) using Table 1.


Table 3. Masses (MeV) of low-lying radially excited triplet l = 0 mesons considered in ( [4] Table 5.7). Data Eexp [5] are given in brackets [..]. Below these are the predicted masses Eth from (10) using Table 1.

The predicted masses Eth are 7% - 18% smaller than the measured ones Eexp in Table 2 and 4% - 18% in Table 3. These differences may tentatively be attributed to the neglected nonlinear potential ΦcJ(r) of (5) in (4) in order to arrive at (10). Actually, (4) and (5) have been solved numerically using an iterative procedure. ( [2] Section 10, [3] Section 7), also explained in ( [4] Section 5.6), for the first and second radially excited singlet and triplet mesons in Section 2 (dm2 = 0). The wave functions as well as the associated nonlinear potential ΦcJ(r) are plotted in ( [2] Figure 1 and Figure 2, [3] Figure 2 and Figure 3). These computations depend upon the choices of unknown parameters, the amplitudes of the wave function in Φc in (2) or the finite sizes of the normalization box Ωc of ( [4] 4.7.5a) or, equivalently, NCJn of ( [3] 4d) which is a volume integral over yJ(r)2. Therefore, the contribution of ΦcJ(r) to Eth can presently not be uniquely determined. More strictly, an 


Qualitatively, follow Section 5.5 of [4] and let ΦcJ(r) in (4) be replaced by constants


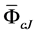

5. Orbitally Excited Singlet Mesons
The wave function is given by ( [4] 3.4.2a), 



As was mentioned in ( [4] §5.7.1), the two solutions for small and large r determined from (12) are independent of the angle θ and are to be connected by an unknown solution dependent upon both r and θ in the intermediate r region. This nonseparable problem starting from ( [4] 3.2.10b) is, as in [4] §5.7.1, beyond the reach of the present work.
Not being to treat this problem adequately, follow the procedures that led to Table 2 and Table 3 in order to obtain some estimates. Linearizing (12) by putting Φc0 = 0, (10) with n = 0 and s = l is obtained. It gives the masses of the mesons in Table 5.8 of [4] listed in Table 4 below.
These results are not surprisingly coarser than those in Table 2 and Table 3 because the neglected nonlinear Φc0 in (12) actually contains angle dependence in the intermediate r region; more equations are required. This turns out actually to be the case; the predicted masses Eth are now 14% - 38% smaller than the measured Eexp, as compared to 9% - 18% for the radially excited mesons. Again replace Φc0 in (12) by constants 

Like the behavior mentioned at the end of Section 4, ΔE2/4 here also increase with the meson masses and, in addition, also with increasing orbital angular momentum l.
Table 4. Masses (MeV) of low-lying orbitally excited l ³ 1 singlet mesons in ( [4] Table 5.8). Data Eexp [5] are given in brackets [..]. Below these are the predicted masses Eth from (10) with n = 0 and s = l using Table 1. The differences 
Note that the predicted values in the second columns in Table 2 and Table 3 are the same for the same quark content. This is due to that (10) cannot distinguish between s = J = 1, l = 0 in Table 3 from J = 0, s = l = 1 in Table 4. The differences are due to that the neglected Fc1 and Fc0 are different; the latter also depends upon the angles in the intermediate r region. The associated radial and orbital quantum numbers nr and l, meaningful at r ® 0 and ¥, are coupled in that region and may lead to a new pair of quantum numbers.
For orbitally excited triplet mesons he classification ( [4] §5.7.2) remains the same.
6. Conclusions
At very low energies, classical mechanics fails and has to be replaced by quantum mechanics, which can however go back to classical mechanics when the energy is sufficiently high. This is not true in the reverse direction. Similarly, QCD fails at low energies and has to be replaced by an appropriate low energy theory, here the SSI, which analogously can go over to QCD in a high energy region [8] , Chapter 14 of [4] . Again, this is not true in the reverse direction.
The role of the nonlinear potential (2) and (5) needs be investigated in an attempt to remove the discrepancies given in the parentheses (…) in Tables 2-4.
The book [4] remains the same up to equation (3.2.19); but (3.2.20), dm2 = 0, needs be changed to dm = 0 which will lead to changes in rest of the book. Thus, the decay rate calculations in Chapters 6-8 need be revised.
Cite this paper
Hoh, F.C. (2017) On Excited Meson Spectra in the Scalar Strong Interaction Hadron Theory. Journal of Modern Physics, 8, 1127-1133. https://doi.org/10.4236/jmp.2017.88073
References
- 1. Burgess, C. and Moore, G. (2007) The Standard Model, A Primer. Cambridge University Press, Cambridge.
- 2. Hoh, F.C. (1993) International Journal of Theoretical Physics, 32, 1111-1133.
https://doi.org/10.1007/BF00671793 - 3. Hoh, F.C. (1996) Journal of Physics G: Nuclear and Particle Physics, 22, 85.
https://doi.org/10.1088/0954-3899/22/1/007 - 4. Hoh, F.C. (2011) Scalar Strong Interaction Hadron Theory. Nova Science Publishers, Hauppauge. (2017) revised second edition, open access at
https://www.novapublishers.com/catalog/product_info.php?products_id = 27069 - 5. Patrignani, C., et al. (Particle Data Group) (2016) Chinese Physics C, 40, 100001.
- 6. Lichtenberg, D.B. (1987) International Journal of Modern Physics A, 2, 1669.
https://doi.org/10.1142/S0217751X87000879 - 7. Ludwig, W. and Falter, C. (1988) Symmetry in Physics. Springer.
- 8. Hoh, F.C. (2013) Journal of Modern Physics, 4, 1171-1175.
https://doi.org/10.4236/jmp.2013.49157


