Journal of Modern Physics
Vol.08 No.05(2017), Article ID:75434,9 pages
10.4236/jmp.2017.85046
Comparison of Calculated Fit and Experimental Calculations of Average Dose Deposited in Aluminum by High Energy Electron Beams
Mohammad Farnush
School of Metallurgy & Materials Engineering, College of Engineering, University of Tehran, Tehran, Iran

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 11, 2017; Accepted: April 14, 2017; Published: April 17, 2017
ABSTRACT
This paper presents the formalism for absorbed dose determination to Aluminum in high-energy electron beams using Rhodotron accelerator. Depth dose curve for Aluminum at electron energy of 10 MeV was calculated. The calculated curve in the model as a function of the depth is compared to the experimental. The agreement of the final results remained well within the expected acceptable range. The calculated values of dose-to-Aluminum are completely fit with the measured values in the range of 0.07% for electron energy of 10 MeV.
Keywords:
Calculated Fit, Average Dose, Aluminum, High Energy Electron Beams

1. Introduction
Researchers presented radiation processing more than 50 years ago [1] , and they have developed many beneficial applications. The most delicate business applications relate to reforming a variance of plastic and rubber productions, and germ-free curative devices and spent items. Appearing applications are posterior and retreat foods, and shortening provisional contamination.
Electron beam gun is an imperative constituent of Gaussian accelerators, which have a difference of applications in examination particularly in high-energy electron beams and industry. In considering electron-positron physics, e-beam is the necessity constituent. This is roughly succeeded throughout thermionic ray of electrons though several other situations of e-beam fabrication as well pursue. This organization of ray has two attitudes: temperature and space charge restrained ray. In first organize; the temperature of the cathode materials restrains the ray while the last ray is restrained by the space charge about the cathode corresponding insufficient acceleration likelihood. Receiving consider its pro- ceeds and repose in fabrication, retaining exercises are observed for the increase of high-energy thermionic electron gun for close origination Gaussian accelerators. These guns obligate fractionally low vacuum and have long liability continual. A critical passage on these types of the guns can be rescued in the referral. In the represent study, electron beam guns used up in some of the well-under- stood high-energy physics laboratories are in short enumerated. Embargo linear accelerator, all references under compassions is thermionic in environment. We as well represent one of our dynamically fabricated sources for conforming and explication with the being sources [2] .
Rhodotrons are electron accelerators correlate the quality of “re-circulating” a beam through consecutive diameters of a singular coequal cavity reverberating in metric waves. Such intension makes it expedient to attain CW acceleration of electron beams to high energies. The primary implication principle of the Rhodotron was first propound in 1989 by J. Pottier from the French Atomic Energy Agency (CEA), who proposed the use of a half-wavelength coequal cavity, shorted at both ends to accelerate electrons. The quality of handling of the Rhodotron has already been enumerated in length in previous articles. The first capitalist Rhodotron (mentioned as model TT-200) was produced in 1993 at IBA Belgium. It surpassed its obligated presentations in 1994 with a maximum beam output power of 110 kW at 10 MeV (100 kW contemplated), and a high power productiveness of 38% at full beam power (25% expected). Three industrialist Rhodotron systems ranging from 35 kW to 200 kW beam power at 10 MeV have been absolutely designed, and are continually constructed at IBA’s specialties in Louvain-la-Neuve. Contingencies of these capitalist accelerators were selected in order to manner the neediness of the outlet of capitalist irradiation for simple, compressed and trustworthy high-power EB units [3] .
Electron accelerators have a wide range of requests in the industry and in the essential examination. Two of the most common issues whilst material irradiation with electron beams are determining the absorbed dose and the reached depth. The approach in each instance adheres on the variety of irradiator, the technological resources and the fantastic usable [4] .
In the designing of high energy electron beam processing, calculation is necessary of the absorbed dose in an example under given irradiation requirements. Even for the most unimportant example arrangement of a glide covering, the issue to be treated is the passing of electrons throughout a covering absorber containing of an accelerator window [5] .
The electron beam already has a specific performance expansion before assembly the accelerator outlet window. This expansion relies on a large number of reasons such as sort of acceleration instrument, procedure of command and withdrawal, and beam manipulation system. The energy spectral at the accelerator outlet window (vacuity side), and may be distinguished by a comparatively mean issue of parameters such as though verified: Emax is the outmost energy, Ea is the average electron energy, Ep, a is the most possible electron energy and Γa is the energy expansion, i.e. the expansion at half maximum of the energy spectral [6] .
Monte Carlo simulations are intensely effective for various physical procedures. The transportation of portions was simulated by Monte Carlo calculating the essential parameters such as contingencies of transmitter-detected and ungainly-energy scattering after interaction with material. The objective of Monte Carlo representation of electron-solid interaction is to simulate the dispersal procedures as correctly as acceptable in the average-energy arrange [7] . This paper fit the dose curve by Monte Carlo but we are not comparing with Molecular dynamics or other methods.
Most of the theoretical accomplish for estimation the absorbed dose in an irradiated matter manipulates calculation procedures. Monte Carlo simulation and straight numerous conclusion of transportation calculation are some useful procedures. However, both of them require enormous CPU time and make necessity the use of high volume computers. In this work, we present a procedure applying a standard private computer for determining indicates of the depth- dose curve of mono-energetic electrons with an energy arrange of 10 MeV. The performed significant allow inside an acceptable arrange, with the experimental estimations. This coherent consents us to have a general experimental procedure to adjust high-energy electron accelerators.
2. Materials and Method
An ionization compartment used (Rhodotron) and its characters are recorded in Table 1. The absorbed dose to Aluminum caliber reasons were supplied by a Secondary Standard Dose Laboratory (SSDL). Complete charge was capacitated with the electroplate example.
The measurements were all performed at the Gaussian accelerator Rhodotron. In the case of high-energy electrons, the two available energies of 5 MeV and 10 MeV. The measurements and comparisons in high-energy electron beams apply to 10 MeV. The method for extracting the depth dose curve by experiment is to put a film on aluminum to measure the dose on the base of the depth.
Basic Formalism
Radiation processing can be determined as the manipulation of maters and produces with radiation or ionizing energy to exchange their physical, chemical or biological characteristics, to enlarge their advantage and value, or to decrease their impact on the circumstance. Accelerated electrons, X-rays (bremsstrahlung) emitted by energetic electrons, and gamma rays emitted by radioactive nuclides are appropriate energy sources. These are all accomplished of ejection atomic electrons, which can then ionize other atoms in an overflow of impacts.
Table 1. Characteristics of Rhodotron.
So they can generate similar molecular induces. The selection of energy source is usually based on effective concepts, such as absorbed dose, dose similarity (max/ min) ratio, mater depth, density and arrangement, computation rate, capital and managing costs [8] .
In the case of electron beam (EB) processing, the contingency electron energy establishes the maximum mater depth, and the electron beam current and power establish the maximum processing rate [9] .
3. Absorbed Dose Definition
The most essential specification for any irradiation process is the absorbed dose. The quantitative effects of the procedure are reported to this factor. Absorbed dose is symmetrical to the ionizing energy delivered per unit mass of mater. The international unit of dose is the gray (Gy), which is determined as the absorption of one joule per kilogram (J/kg) [9] . A more accessible unit for most radiation processing applications is the kilo gray (kJ/kg or J/g). An older unit is the rad, which is determined as the absorption of 100 ergs per gram or 10 - 5 joules per gram. So, 100 rads is equivalent to 10 - 3 joules per gram or 1 joule per kilogram or 1 gray. The rad unit is now obsolete, but several marketable procedures are still categorized in rads, kilorads or megarads [10] .
The relationship between absorbed dose of Aluminum and electron energy deposition of Aluminum can be derived in the following manner:
 (1)
(1)
Absorbed dose of Aluminum = 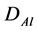
Absorbed energy of Aluminum = 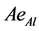
Mass of Aluminum = 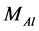
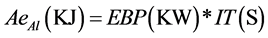 (2)
(2)
Electron Beam Power (KW) = EBP
Irradiation Time (S) = IT
 (3)
(3)
Electron Energy = 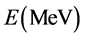
Electron Beam Current = 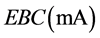
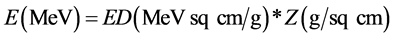 (4)
(4)
Energy Deposition per Incident Electron per unit area Density =
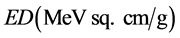
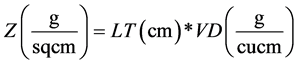 (5)
(5)
Layer Thickness of Aluminum = 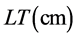
Volume Density of Aluminum = 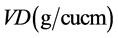
Then Equation (1) can be modified as follow:
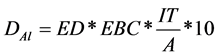 (6)
(6)
Absorbed Dose at depth z in the irradiated Aluminum = 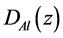
Energy Deposition per Electron at Depth z in the irradiated Aluminum =
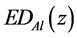
Fraction of Emitted Beam Current intercepted by the irradiated Aluminum = 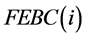
Then Equation (6) can be modified as follow:

4. Results
The penetration of the fast electrons through the material is the respectable subject of the theoretical and experimental explorations. Multiple Coulomb dissipation and statistical uncertainty in ionization energy loss distinguish it. The transportation attributes of electrons are also of attention in correlation with great experimental applications. When the absorber maters are thin enough resembled to the range of contingency electrons, the problems can be disciplined analytically and the adequate coherence between theory and experiment has been reported [11] .
The condition becomes more perplexed when the absorber thickness expansions. For this case, the energy loss and ungainly deflection cannot be handled exclusively and theoretical treatment of the problem is very puzzling. There are two procedures to study electron transport in the thick maters; the moment’s arrangement and the Monte Carlo method. The moments method progressed by Spencer’ has been used to calculate the depth distribution of energy deposition in the maters. Nevertheless, its application is confined only to media that are released and comparable, and foil-transmission problems cannot be handled by this procedure [11] .
On the other hand, the Monte Carlo method can, in opinion, present the most methodical resolutions for the electron transport problems in confined media. This procedure is appropriate to any energy range of electrons and to any geometry. The calculation is based on the simulation of the electron tracks by incidental sampling techniques. The numerate of Coulomb accidents undergone by a fast electron while the slowing-down procedure is exactly big, so that the simulation of the individual impact is not feasible. Instead, the electron trajectory is separated into a numerate of short sections, such that the numerate of impacts along each section is big, however the average ungainly duplicated due to varied scattering and the average energy loss by ionization per section are small. This means that the conclusions of systematic managements of angular multiples and energy losses can give adequate propinquities to the net contingency dispersions in each section. The angular deflections and energy losses inspected in each section are then connected to fabricate a complete electron trajectory in the foil. By the use of such a method, the thick-foil transfer problem can be handled as a consequence of thin-foil ones, in which logical forms can satisfactory present the electron performance [11] .
Berger has informed the Monte Carlo procedure based on this perspective, and the previously references are cited therein. Recently, Sugiyama’ executed Monte Carlo estimations for transportation of fast electrons with energy higher than a few MeV and acquired the conclusions in extremely good agreement with experimental data. Berger and Seltzer progressed a computer code entitled ETRAN, (“which the most actual and the most repeatedly used program is at present. by the use of this code they estimated disparate quantities for electron transmittal”) and for construction of bremsstrahlung radiation. Using the same intellect as those manipulated in the ETRAN code, many codes have been developed to authorize the practice studying of the electron transportation problems for one-dimensional multilayer objectives (“cylindrical-geometry multi-maters’ and combined procedures [11] ”).
Regardless the ETRAN code is actual, takes into consider several interactions between electron and atom, and has the flexibility of being able to estimate disparate quantities, it obligates a large-memory and high-speed computer. In the case of radioactive sources, most electrons speeded from the source have the energy less than 2 MeV [11] .
In this paper is presented a brief narration of a Calculated Fit program to study transmittal of electrons through Aluminum. This program comprehends electron complicated scattering and the exestuation of energy-loss straggling. The usefulness is its clearness and high speed. The present code does not obligate large-memory computer and is adequately actual. Estimations have been conveyed with this code for mono-energetic electrons incident perpendicularly on the objectives of different depth. The consequences presented here contain the transmission coefficient and the energy spectral of transmitted electrons. Proportion is made with the experimental conclusions and also with the estimated result from the Calculated Fit code [11] .
A fundamental problem in the dosimetry of electrons is the estimation of the average absorbed dose disclosed to a mater suspicion perpendicular by a homogeneous plane-parallel broad beam of mono-energetics electrons. Yet the complications of scattering, straggling, and the production and escape of delta-rays and bremsstrahlung may cause inaccuracies in simple analytical calculations using CSDA (continuous slowing down approximation) stopping-power or range tables such as those of Berger and Seltzer (1983) [11] .
In the present paper analytical calculations of dose that depend on various conjectures about the complication processes are carried out, and are compared with corresponding Calculated Fit computations which provide the quantities shown in Figure 1 [11] .
To compare Calculated Fit with dose determinations, a model of a flat sheet of aluminum moving continuously through a wide electron beam was used. The quantities that must be known are:
1) The contingency electron energy,
2) The accelerated beam current,
3) The fraction of beam current overtook by the irradiated mater,
Figure 1. Depth dose curve for aluminum at electron energy of 10 MeV. The calculated curve in the model (__) as a function of the depth is compared to the experimental (.).
4) The atomic composition and depth of the beam window,
5) The air space between the beam window and the irradiated mater,
6) The dosimeters and any covering or supporting maters,
7) The composition, width and thickness of the irradiated mater and
8) The conveyor speed. The Calculated Fit code calculates the Dose, 
4.1. Method of Calculation
The Calculated Fit has been calculated under the following assumptions:
1) An electron beam is incident normally on aluminum.
2) The lateral extension of the aluminum is large enough compared to the electron range.
3) The electrons never return to the aluminum once they have left it.
4) The production of knock-on electrons by the inelastic Coulomb collisions is ignored.
5) The energy loss by radiation is neglected [11] .
4.2. Analytical Calculation
For this simplest case we make the assumptions:
1) The electrons that enter the Aluminum pass straight through without scattering.
2) The stopping power value for the incident energy r, applies throughout the electron path length, but the maximum energy spent in the Aluminum is limited to T, 

3) Any bremsstrahlung that is produced escapes.
4) Delta-ray effects are negligible.
5) Electron backscattering is negligible [11] .
The results obtained from the Calculated Fit in the model for the Dose-Depth distribution and experimental are given in Figure 1. The depth-dose distribution given by the present algorithm has been compared with experimental.
Smoothing spline:

Dose =
Smoothing parameter:
P = 0.99992527
Goodness of fit:
SSE: 0.007257
R-square: 0.9996
Adjusted R-square: 0.9988
RMSE: 0.03167
5. Discussion
In the characterization of the electron beam, it is usable to declare some specialty of the procedure represented here. Firstly, it is very simple and it allows us to have an average value of the current density. However, from the digitized spots of the beam of our system it is possible to infer the arrangement profile.
The results of absorbed dose according to Aluminum obtained with the one chamber was apparently highly consistent, if the result with the Rhodotron chamber at 10 MeV is included. The good agreement, however, is simply a result of the fact that equation 8 was used to derive appropriate [11] .
6. Conclusions
The calculated values of dose-to-Aluminum are completely fit with the measured values in the range of 0.07% for electron energy of 10 MeV. Possible explanations for these small differences have not been investigated. Even so, the relatively close agreement is satisfying when the extreme differences in dose rate (10000/1) and type of radiation (electrons versus gamma rays) are considered. This study confirms that the response of this type of dosimeter system is independent of the dose-rate, and it provides assurance that Calculated Fit calculations can give results with sufficient accuracy for many industrial applications of radiation processing [11] .
The present approach describes the penetration of the primary electrons for aluminum and with considerable success. A comparatively simple model gives a reasonable description of electron scattering for energy of 10 MeV. The scattering processes involve elastic and inelastic scattering. The calculation provided the energy spectra and angular distributions of transmitted and reflected electrons for aluminum by Calculated Fit approach. Fitting results for transmission experiments are presented and compared with experimental data for electron energy of 10 MeV. Such a Calculated Fit procedure can be efficiently used to fit the experimental conditions encountered in surface electron spectroscopy [11] .
Acknowledgements
We acknowledge technical and scientific help of University of Tehran.
Cite this paper
Farnush, M. (2017) Comparison of Calculated Fit and Experimental Calculations of Average Dose Deposited in Aluminum by High Energy Electron Beams. Journal of Modern Physics, 8, 747-755. https://doi.org/10.4236/jmp.2017.85046
References
- 1. Mehnert, R. (1996) Nuclear Instruments and Methods in Physics Research, 113, 81-87.
- 2. Iqbal, M., Islam, G.U., Farida, M.A. and Zhou, Z. (2013) Journal of Modern Physics, 4, 1536-1539.
https://doi.org/10.4236/jmp.2013.411188 - 3. Jongen, Y., Abs, M., Delvigne, T., Herer, A., Capdevila, J.M., Genin, F. and Nguyen, A. (1996) Rhodotron Accelerators for Industrial Electron-Beam Processing: A Progress Report. EPAC96, 5th European Particle Accelerator Conference, Sitges, Spain, 10-14 June 1996, 2687-2689.
- 4. Vazquez-Polo, G., Lopez Valdivia, H., Carrasco, H.A., Mijangos, R.R. and Garcia, R.G. (2002) Radiation Physics and Chemistry, 64, 181-187.
- 5. Tabata, T., Ito, R. and Tsukui, S. (1990) Radiation Physics and Chemistry, 35, 821-825.
- 6. (1987) Absorbed Dose Determination in Photon and Electron Beams. International Atomic Energy Agency, Vienna.
- 7. Aydin, A. and Peker, A. (2015) Nukleonika, 60, 361-366.
https://doi.org/10.1515/nuka-2015-0035 - 8. Takeshi, M. and Yoshihisa, M.W. (1977) Bulletin of the Institute for Chemical Research (Kyoto University), 55, 46-59.
- 9. Attix, F.H. (1991) International Journal of Radiation Applications and Instrumentation. Part A. Applied Radiation and Isotopes, 42, 953-964.
- 10. McLaughlin, W.L., et al. (1989) Dosimetry for Radiation Processing. Taylor & Francis, New York.
- 11. Cleland, M.R., Galloway, R.A., Heiss, A.H.J. and Logar J.R. (2007) Nuclear Instruments and Methods in Physics Research B, 261, 90-93.




