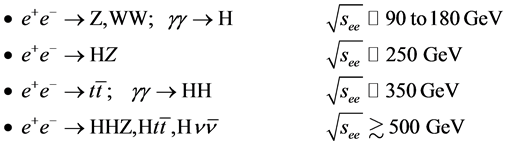Journal of Modern Physics
Vol.08 No.01(2017), Article ID:72598,16 pages
10.4236/jmp.2017.81001
An SLC-Type  Facility at a Future Circular Collider
Facility at a Future Circular Collider
Radoje Belusevic
High Energy Accelerator Research Organization (KEK), Tsukuba, Japan

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 1, 2016; Accepted: December 4, 2016; Published: December 7, 2016
ABSTRACT
It is proposed to place the arcs of an SLC-type facility inside the tunnel of a Future Circular Collider (FCC). Accelerated by a linear accelerator (linac), electron and positron beams would traverse the bending arcs in opposite directions and collide at centre-of-mass energies considerably exceeding those attainable at circular 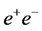 colliders. The proposed SLC-type facility would have the same luminosity as a conventional two-linac
colliders. The proposed SLC-type facility would have the same luminosity as a conventional two-linac 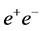 collider. Using an optical free-electron laser, the facility could be converted into a
collider. Using an optical free-electron laser, the facility could be converted into a 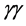 collider. A superconducting L-band linac at the proposed facility may form a part of the injector chain for a 100-TeV proton collider in the FCC tunnel. The whole accelerator complex would serve as a source of
collider. A superconducting L-band linac at the proposed facility may form a part of the injector chain for a 100-TeV proton collider in the FCC tunnel. The whole accelerator complex would serve as a source of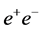 ,
, 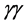 ,
, 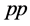 and
and 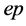 interactions. The L-band linac could also be used to produce high-intensity neutrino, kaon and muon beams for fixed-target experiments, as well as X-ray free-electron laser (XFEL) photons for applications in material science and medicine.
interactions. The L-band linac could also be used to produce high-intensity neutrino, kaon and muon beams for fixed-target experiments, as well as X-ray free-electron laser (XFEL) photons for applications in material science and medicine.
Keywords:
Particle Collider, Higgs Physics, Superconducting Linac

1. Introduction
The Standard Model (SM) of particle physics gives a coherent quantum-mechanical description of electromagnetic, weak and strong interactions based on fundamental constituents―quarks and leptons―interacting via force carriers―photons, W and Z bosons, and gluons. The SM is supported by two theoretical “pillars”: the gauge prin- ciple and the Higgs mechanism for particle mass generation. In the SM, where electro- weak symmetry is broken by the Higgs mechanism, the mass of a particle depends on its interaction with the Higgs field, a medium that permeates the universe. The photon and the gluon do not have such couplings, and so they remain massless. The SM predicts the existence of a neutral spin-0 particle associated with the Higgs field, but it does not predict its mass.
Whereas the gauge principle has been firmly established through precision electro- weak measurements, the Higgs mechanism is yet to be fully tested. A state decaying to several distinct final states was observed in 2012 at the CERN Large Hadron Collider (LHC) with a statistical significance of five standard deviations [1] [2] . The observed state has a mass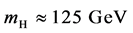 . Its production rate is consistent with the predicted rate for the SM Higgs boson. Furthermore, event yields in different production topolo- gies and different decay modes are self-consistent [3] .
. Its production rate is consistent with the predicted rate for the SM Higgs boson. Furthermore, event yields in different production topolo- gies and different decay modes are self-consistent [3] .
All of the couplings of the Higgs particle to gauge bosons and fermions are com- pletely determined in the SM in terms of electroweak coupling constants and fermion masses. In the SM, Higgs production and decay processes can be computed un- ambiguously in terms of the Higgs mass. Since the coupling of the Higgs boson to fermions and gauge bosons is proportional to the particle masses, the Higgs boson is produced in association with heavy particles and decays into the heaviest particles that are kinematically accessible.
The Higgs-boson mass affects the values of electroweak observables through radia- tive corrections. Many of the electroweak measurements obtained over the past three decades may be combined to provide a global test of consistency with the SM. The best constraint on 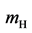 is obtained by making a global fit to the electroweak data. Such a fit strongly suggests that the most likely mass for the SM Higgs boson is just above the limit of 114.4 GeV set by direct searches at the LEP
is obtained by making a global fit to the electroweak data. Such a fit strongly suggests that the most likely mass for the SM Higgs boson is just above the limit of 114.4 GeV set by direct searches at the LEP 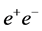 collider [4] . This is con- sistent with the value of the Higgs mass measured at LHC.
collider [4] . This is con- sistent with the value of the Higgs mass measured at LHC.
High-precision electroweak measurements, therefore, provide a natural complement to direct studies of the Higgs sector. All the measurements made at LEP and SLC could be repeated at the proposed facility using 90% polarized electron beams and at much higher luminosities [5] .
The rich set of final states in 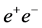 and
and 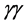 collisions at the proposed SLC-type facility would play an essential role in measuring the mass, spin, parity, two-photon width and trilinear self-coupling of the SM Higgs boson, as well as its couplings to fermions and gauge bosons. Such measurements require centre-of-mass (c.m.) energies
collisions at the proposed SLC-type facility would play an essential role in measuring the mass, spin, parity, two-photon width and trilinear self-coupling of the SM Higgs boson, as well as its couplings to fermions and gauge bosons. Such measurements require centre-of-mass (c.m.) energies , considerably exceeding those attainable at circular
, considerably exceeding those attainable at circular 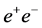 colliders.
colliders.
2. Single SM Higgs Production in 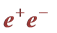 Annihilations
Annihilations
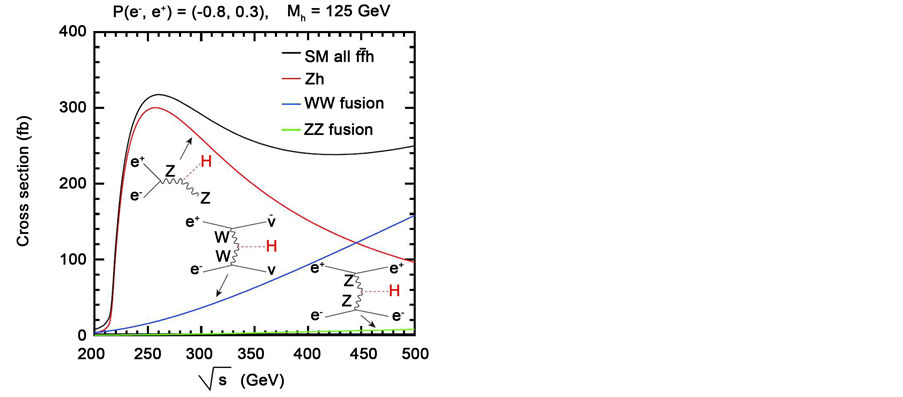
A particularly noteworthy feature of an 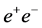 collider is that the Higgs boson can be detected in the Higgs-strahlung process (see Figure 1)
collider is that the Higgs boson can be detected in the Higgs-strahlung process (see Figure 1)
 (1)
(1)
even if it decays into invisible particles (e.g., the lightest neutralino of a supersymmetric model). In this case the signal manifests itself as a peak in the invariant mass distri- bution of the system which recoils against the lepton pair stemming from Z-boson decay. In Equation (1), 
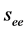
By exploiting the 
Figure 1. Centre-of-mass energy dependence of the cross-sections for SM Higgs-boson pro- duction in the Higgs-strahlung, W-fusion and Z-fusion processes [7] . Note that one has to measure separately the couplings HWW, HHH and Htt at 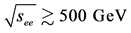
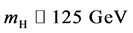
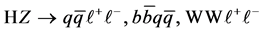
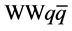
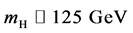
To determine the spin and parity of the SM Higgs boson in the Higgs-strahlung process, one can use the information on (1) the energy dependence of the Higgs-boson production cross-section just above the kinematic threshold, and (2) the angular distribution of the Z/H bosons. The best way to study the CP properties of the Higgs boson is by analyzing the spin correlation effects in the decay channel 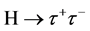
The Higgs-strahlung cross-section, which dominates at low c.m. energies, decreases with energy in proportion to
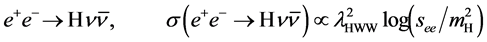
increases with energy in proportion to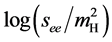
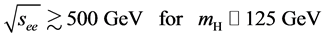
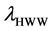
The Higgs-fermion couplings can be extracted by measuring the branching fractions of the Higgs boson. There are two methods to determine the Higgs branching fractions: (1) Measure the event rate in the Higgs-strahlung process for a given final-state configuration and then divide by the total cross-section; (2) Select a sample of unbiased events in the Higgs-strahlung recoil-mass peak and determine the fraction of events that correspond to a particular decay channel. See [6] and references therein for an estimate of the accuracy that can be achieved in such measurements.
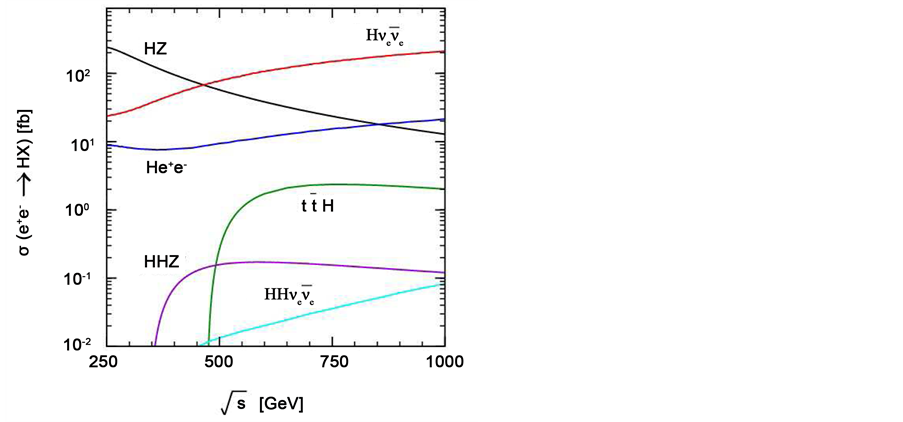
For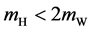
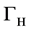
Figure 2. Centre-of-mass energy dependence of various cross-sections for single and double SM Higgs-boson production in 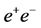
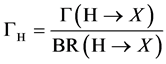
For instance, consider the decay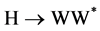
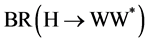
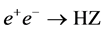
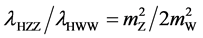
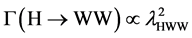
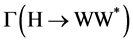
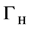
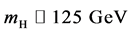
3. Single SM and MSSM Higgs Production in 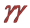
Since photons couple directly to all fundamental fields carrying the electromagnetic current (leptons, quarks, W bosons, supersymmetric particles), 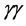
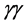

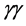
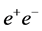
In 
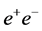
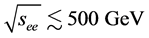
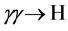
is at least a factor of four larger than any cross-section for Higgs production in 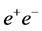
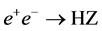

Any theoretical model based on the gauge principle must evoke spontaneous symmetry breaking. In the minimal supersymmetric extension of the Standard Model (MSSM), for instance, spontaneous electroweak symmetry breaking results in five physical Higgs-boson states: two neutral scalar fields 

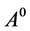
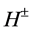
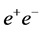
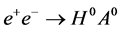
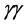

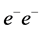
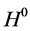
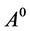
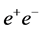
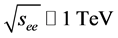
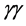
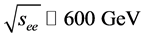
The reaction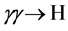

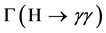
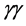
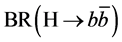
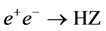
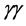
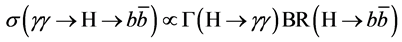
Each of the decay modes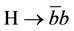
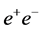
High-energy photons can be produced by Compton-backscattering of laser light on electron beams. Both the energy spectrum and polarization of the backscattered photons depend strongly on the polarizations of the incident electrons and laser photons. The key advantage of using 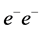
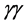
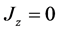

The CP properties of any neutral Higgs boson that may be produced at a photon collider can be directly determined by controlling the polarizations of Compton- scattered photons [13] . A CP-even Higgs boson couples to the combination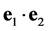

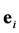
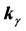
The general amplitude for a CP-mixed state to couple to two photons can be expressed as
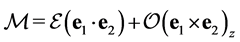
where 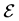

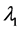
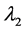
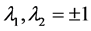
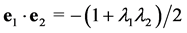
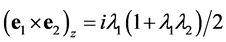
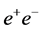
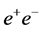
A study of single Higgs-boson production in 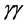
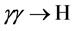
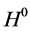
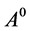
To ascertain the physics potential of a 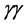
4. Higgs-Pair Production in 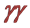
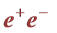
It is well known that hadron colliders are not ideally suited for measuring the self- coupling of the Higgs boson if 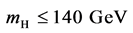
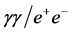
The production of a pair of SM Higgs bosons in photon-photon collisions,
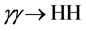
which is related to the Higgs-boson decay into two photons, is due to W-boson and top-quark box and triangle loop diagrams. The total cross-section for 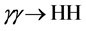
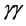
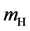
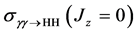
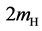
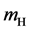
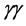
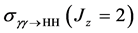

The cross-sections for equal photon helicities are of special interest, since only the 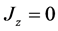
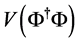
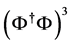
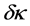
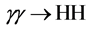
Figure 3. The cross-sections for HH production in 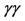
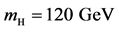

replace the trilinear Higgs coupling of the SM, 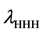
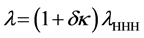
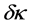
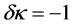
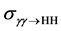
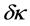
In an experiment to measure the trilinear Higgs self-coupling, the contribution from 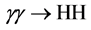
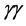
The Feynman diagrams for the process 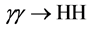
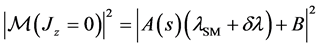
where 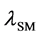
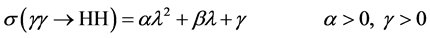
is a quadratic function of the coupling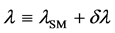
The trilinear self-coupling of the Higgs boson can also be measured either in the so-called double Higgs-strahlung process

or in the W-fusion reaction
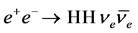
The total cross-section for pair production of 120-GeV Higgs bosons in 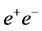
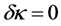
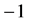
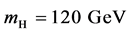
For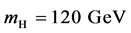
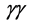
Figure 4. The total cross-sections for 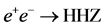
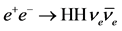
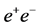
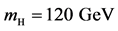
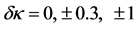
Calculations show that the statistical sensitivity of 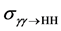

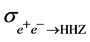
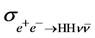
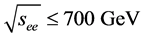

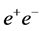


Since the cross-section 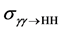
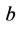
The results of detailed feasibility studies for measuring Higgs-pair production in 
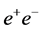
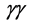
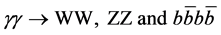
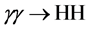
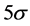
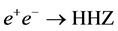
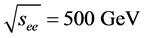
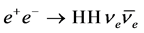
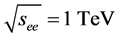
5. The Proposed Facility
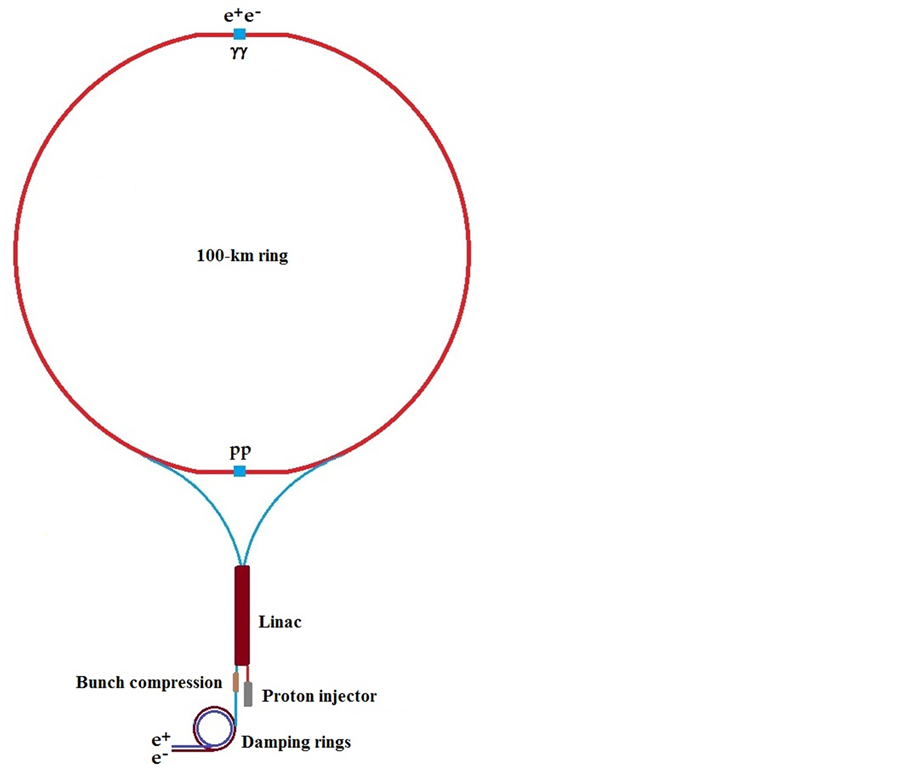
A schematic layout of the proposed SLC-type 
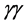
With a crossing angle at the interaction point (IP), separate beam lines may be used to bring the disrupted beams to their respective dumps, thereby enabling post-IP diagnostics. It is also envisaged that a “bypass line” for low-energy beams would be employed to accumulate data at the Z resonance in the process
The proposed facility could be constructed in several stages, each with distinct physics objectives that require particular center-of-mass (c.m.) energies:
Figure 5. Schematic layout of the proposed SLC-type facility. A 350-GeV superconducting linac (with a focusing quadrupole in each cryomodule) could also be a part of the FCC injector chain.
For instance, the top-quark mass could be measured in the process 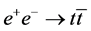
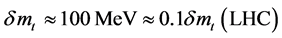
The linac at the proposed SLC-type facility would consist either of (1) high-gradient X-band cavities developed for CLIC and a corresponding klystron-based power source (a two-beam scheme could be implemented at a later stage); or (2) ILC-type supercon- ducting L-band cavities placed within cryogenic vessels and fed by multi-beam klystrons.
The 11.4 GHz X-band rf technology was originally developed at SLAC and KEK. The choice of this technology is motivated by the cost benefits of having relatively low rf energy per pulse and high accelerating gradients. A comprehensive review of the status of X-band accelerator technology is given in [28] . Since then, significant advances have been made in pulsed HV and rf power generation, high gradient acceleration and wakefield suppression. The ultimate design of rf cavities will depend on the outcome of the ongoing effort to develop 100 MeV/m X-band structures for a CLIC-type linear collider.
As proposed in [23] , a single X-band rf unit contains a modulator that drives a pair of 50 MW klystrons, each of which generates 1.6 μs rf pulses at 50 Hz. An rf compression system enhances the peak power of the klystrons by a factor of 3.75, and produces 245 ns pulses that match the accelerator structure requirements. The resulting 375 MW, 245 ns pulses feed seven 0.21m-long accelerator structures, producing a 85 (100) MV/m loaded (unloaded) gradient in each structure.
The current design for the International Linear Collider (ILC), based on the super- conducting technology originally developed at DESY, uses L-band (1.3 GHz) super- conducting niobium rf cavities that have average accelerating gradients of 31.5 MeV/m (see [29] and references therein). Nine cavities, each 1 m long, are mounted together in a string and assembled into a common low-temperature cryostat or cryomodule. Liquid helium is used to cool cavities to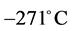
An ILC-type main linac is composed of rf units, each of which is formed by three contiguous cryomodules containing 26 nine-cell cavities. Every unit has an rf source, which includes a pulse modulator, a 10 MW multi-beam klystron, and a waveguide system that distributes the power to the cavities. An ILC-type design offers some advantages over the X-band technology:
Wakefields are drastically reduced due to the large size of the rf cavities, which means that cavity alignment tolerances can be relaxed. This is crucial for an SLC-type facility, where both 
Superconducting rf cavities can be loaded using a long rf pulse (1.5 ms) from a source with low peak rf power;
Wall-plug to beam’ power transfer efficiency is about twice that of X-band cavities;
The long rf pulse allows a long bunch train (~1 ms), with many bunches (~3000) and a relatively large bunch spacing (~300 ns). A trajectory correction (feedback) system within the train can therefore be used to bring the beams into collision.
However, in contrast to a compact, high-gradient X-band machine, a collider based on the current ILC-type design would be characterized by (a) low accelerating gradients; (b) two large damping rings with a total length of at least six kilometers, and (c) a technologically challenging cryogenic system that requires a number of surface cryo- genic plants.
An important feature of the proposed SLC-type facility is the possibility of using backscattered laser beams to produce high-energy 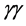
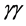
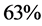
These requirements could be satisfied by an optical free electron laser (FEL) [30] . The radiation produced by an FEL has a variable wavelength, and is fully polarized either circularly or linearly depending on whether the undulator is helical or planar, respectively. The wavelength 


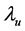
Assuming that the mean number of Compton interactions of an electron in a laser pulse (the Compton conversion probability) is 1, the conversion coefficient
where 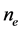
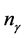
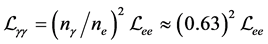
where 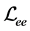

In this expression, 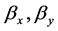
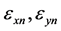
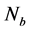
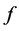
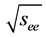
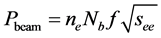
There are 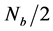
The energy loss per turn due to synchrotron radiation (SR) in a storage ring is given by
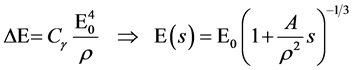
where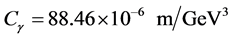
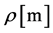
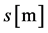
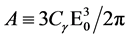
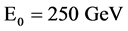
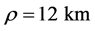
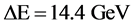
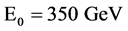
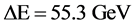
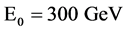
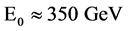
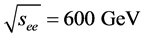
The critical energy of SR photons, 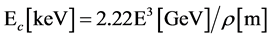
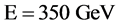
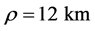
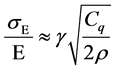
where 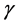
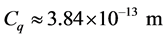
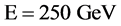

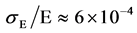

In contrast to ILC or CLIC, an SLC-type collider would have a single bunch compression system and a short beam transfer line connecting the damping rings with the entrance to the main linac (see Figure 5). A 350-GeV superconducting L-band linac at the proposed facility may form, together with a 3-TeV energy booster, the injector
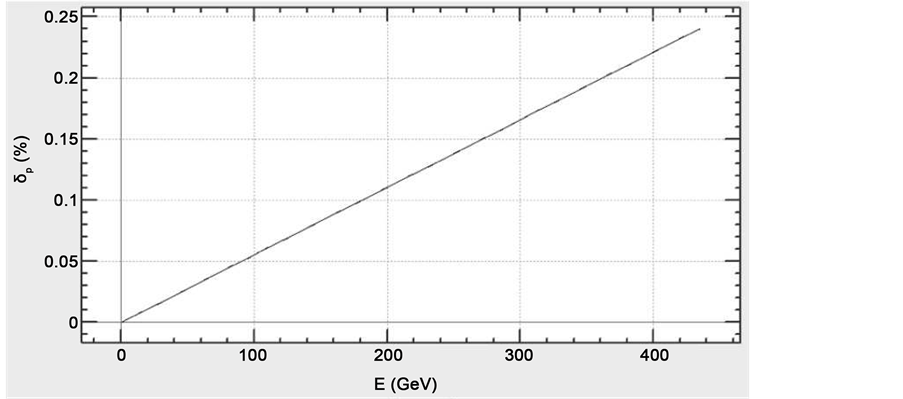
Figure 6. Energy spread in an electron beam traversing an arc with an effective bending radius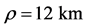
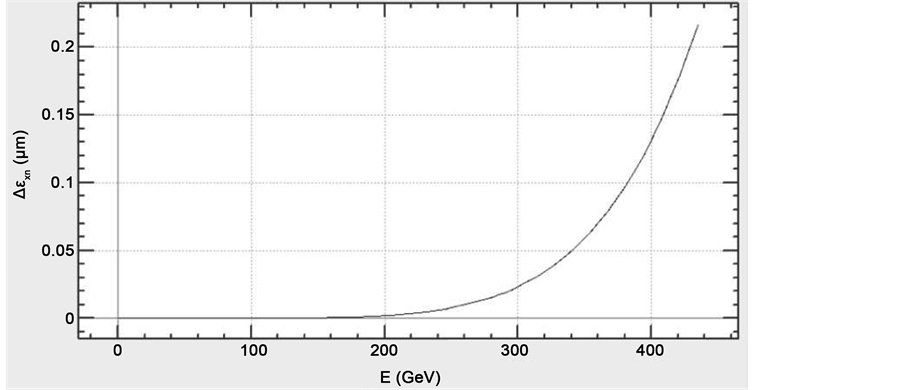
Figure 7. Energy dependence of the growth of the horizontal electron beam emittance in an arc with an effective bending radius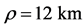
chain for a proton collider in the FCC tunnel (e.g., the linac could replace the chain LINAC4 → PSB → PS → SPS at CERN).
6. Concluding Remarks
It is proposed to place the arcs of an SLC-type facility inside the 100 km long tunnel of a Future Circular Collider (FCC). Electron and positron beams, accelerated in a single X-band or L-band linac, would traverse the arcs of bending magnets in opposite directions (see Figure 5) and collide at c.m. energies considerably exceeding those attainable at circular 

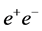
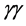
The proposed 
The maximum luminosity at a circular 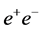
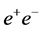
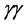
It is straightforward to convert an SLC-type facility into a high-luminosity 
A 350-GeV superconducting L-band linac at the proposed facility may form, together with a 3-TeV energy booster, the injector chain for a 100-TeV proton collider in the FCC tunnel. The L-band linac could also be used to produce high-intensity neutrino, kaon and muon beams for fixed-target experiments, as well as X-ray FEL photons for applications in material science and medicine [34] .
If electron or positron bunches, accelerated by the L-band linac at the proposed facility, are brought into collision with the 50-TeV FCC proton beams, the whole accelerator complex could serve also as a source of deep-inelastic 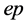
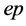
The rich set of final states in 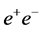

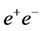
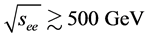
For some processes within and beyond the SM, the required c.m. energy is con- siderably lower in 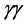
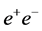
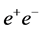
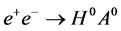

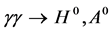
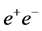
Both the energy spectrum and polarization of the backscattered photons at a 
Acknowledgements
I would like to thank I. Ginzburg, T. Higo, A. Wolski and K. Yokoya for valuable comments and suggestions concerning various aspects of this proposal. I am especially grateful to K. Oide and D. Zhou for helping me estimate some relevant beam properties at the proposed facility.
Cite this paper
Belusevic, R. (2017) An SLC-Type
References
- 1. Aad, G., et al., ATLAS Collaboration (2012) Physics Letters B, 716, 1-29.
https://doi.org/10.1016/j.physletb.2012.08.020 - 2. Chatrchyan, S., et al., CMS Collaboration (2012) Physics Letters B, 716, 30-61.
https://doi.org/10.1016/j.physletb.2012.08.021 - 3. Beringer, J., et al., Particle Data Group (2012) Physical Review D, 86, 010001.
- 4. Barate, R., et al., The LEP Working Group for Higgs Boson Searches (2003) Physics Letters B, 565, 61-75.
https://doi.org/10.1016/S0370-2693(03)00614-2 - 5. Erler, J., et al. (2000) Physics Letters B, 486, 125-133.
https://doi.org/10.1016/S0370-2693(00)00749-8 - 6. Heinemeyer, S., et al. (2005) Toward High Precision Higgs-Boson Measurements at the International Linear e+e− Collider. hep-ph/0511332.
- 7. Fujii, K., et al. (2015) Physics Case for the International Linear Collider. arXiv: 1506.05992v1.
- 8. Asner, D., et al. (2013) ILC Higgs White Paper. arXiv:1310.0763v3.
- 9. Boos, E., et al. (2001) Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 472, 100-120.
https://doi.org/10.1016/S0168-9002(01)01168-8 - 10. Belusevic, R. (2003) Low-Energy Photon Collider. KEK Preprint 2003-2.
- 11. Mühlleitner, M., Krämer, M., Spira, M. and Zerwas, P.M. (2001) Physics Letters B, 508, 311-316.
https://doi.org/10.1016/S0370-2693(01)00321-5 - 12. Asner, D., et al. (2003) European Physical Journal C, 28, 27-44.
https://doi.org/10.1140/epjc/s2002-01113-3 - 13. Grzadkowski, B. and Gunion, J. (1992) Physics Letters B, 294, 361-368.
https://doi.org/10.1016/0370-2693(92)91534-G - 14. Hagiwara, K. (2001) Nuclear Instruments and Methods in Physics Research Section A, 472, 12-21.
https://doi.org/10.1016/S0168-9002(01)01157-3 - 15. Doncheski, M. and Godfrey, S. (2003) Resolved Photon Contributions to Higgs Boson Production in γγ Collisions. arXiv:hep-ph/0105070v2.
- 16. Ginzburg, I., Kotkin, G.L., Serbo, V.G. and Telnov, V.I. (1983) Nuclear Instruments and Methods, 205, 47-68.
https://doi.org/10.1016/0167-5087(83)90173-4 - 17. Baur, U., Plehn, T. and Rainwater, D.L. (2003) Physical Review D, 68, Article ID: 033001.
https://doi.org/10.1103/PhysRevD.68.033001 - 18. Belusevic, R. and Jikia, G. (2004) Physical Review D, 70, Article ID: 073017.
https://doi.org/10.1103/PhysRevD.70.073017 - 19. Djouadi, A., et al. (1999) European Physical Journal C, 10, 27.
- 20. Miller, D.J. and Moretti, S. (2000) European Physical Journal C, 13, 459-470.
https://doi.org/10.1007/s100520000248 - 21. Castanier, C., et al. (2001) Higgs Self Coupling Measurement in e+e− Collisions at Center-of-Mass Energy of 500 GeV. hep-ex/0101028.
- 22. Belanger, G., et al. (2003) Physics Letters B, 576, 152-164.
https://doi.org/10.1016/j.physletb.2003.09.080 - 23. Belusevic, R. and Higo, T. (2012) A CLIC-Prototype Higgs Factory. arXiv:1208.4956v3.
- 24. Jikia, G. (1994) Nuclear Physics B, 412, 57-75.
https://doi.org/10.1016/0550-3213(94)90494-4 - 25. Kawada, S., et al. (2012) Physical Review D, 85, Article ID: 113009.
https://doi.org/10.1103/PhysRevD.85.113009 - 26. Tian, J. (2013) LC-REP-2013-003.
- 27. Fujii, K., Matsui, T. and Sumino, Y. (1994) Physical Review D, 50, 4341.
https://doi.org/10.1103/PhysRevD.50.4341 - 28. Adolphsen, C. (2005) Advances in Normal Conducting Accelerator Technology from the X-Band Linear Collider Program. 2005 Particle Accelerator Conference, Knoxville, 16-20 May 2005.
- 29. Barish, B. and Brau, J. (2013) International Journal of Modern Physics A, 28, Article No.: 1330039.
- 30. Saldin, E., Schneidmiller, E. and Yurkov, M. (2001) Nuclear Instruments and Methods in Physics Research Section A, 472, 94-99.
https://doi.org/10.1016/S0168-9002(01)01167-6 - 31. Michelato, P. (2008) Proc. EPAC08, Genoa.
- 32. Koratzinos, M. (2015) The FCC-ee Design Study: Luminosity and Beam Polarization.
arXiv:1511.01021v1. - 33. Moortgat-Pick, G., et al. (2015) European Physical Journal C, 75, 371.
https://doi.org/10.1140/epjc/s10052-015-3511-9 - 34. Belusevic, R. (2014) A Multi-MW Proton/Electron Linac at KEK.
arXiv:1411.4874v1 and KEK Preprint 2014-35. - 35. Acar, Y.C., et al. (2016) Main Parameters of LC × FCC Based Electron-Proton Colliders.
arXiv: 1602.03089v1. - 36. Abelleira Fernandez, J.L. (2012) Journal of Physics G: Nuclear and Particle Physics, 39, Article ID: 075001.
- 37. McCullough, M. (2014) An Indirect Model-Dependent Probe of the Higgs Self-Coupling.
arXiv: 1312.3322v6.