Journal of Modern Physics
Vol.07 No.10(2016), Article ID:67185,4 pages
10.4236/jmp.2016.710093
The Problem on Stationary States in Self Gravitational Field
Stanislav Fisenko
“Rusthermosinthes” JSC, Moscow, Russia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2016; accepted 3 June 2016; published 8 June 2016
ABSTRACT
To follow is the problem on stationary states of an electron in its own gravitational field where the boundary conditions earlier described in [1] are made specific. The simplest approximation provides an assessment of the energy spectrum of stationary states only. Nevertheless, this is enough to confirm the existence of such stationary states and to further elaborate a detailed solution of the problem on stationary states including determination of all the quantum numbers’ spectra and corresponding wave functions. No other matters are discussed here. The case in hand is a purely mathematical problem, further physical interpretation of which is of a fundamental value.
Keywords:
Gravity, Electron, Irremovable Space-Time Curvature, Spectrum

1. Introduction
The physical nature of the problem under consideration hereinafter can be briefly summarized as follows [1] . Generally covariant relativistic form of the equations of Einstein’s theory of gravitation, as we know, has the following form:
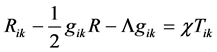 (1)
(1)
In these equations 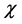 is a constant that relates to the geometrical properties of space-time distribution of physical matter, so that the origin of the equations is not associated with the numerical restriction of the values. Only the requirements of compliance with the Newton’s law of universal gravitation leads to numerical values
is a constant that relates to the geometrical properties of space-time distribution of physical matter, so that the origin of the equations is not associated with the numerical restriction of the values. Only the requirements of compliance with the Newton’s law of universal gravitation leads to numerical values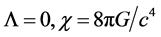 , where G is the Newton’s gravitational constant. Equation with certain constants determined in this way is the equations of the Einstein’s theory of general relativity. Equation (1) is a common mathematical form of the gravitational field equations corresponding to the principle of equivalence and the postulate of general covariance. The equations of the form (1) are obtained simultaneously by Einstein and independently by Gilbert [2] . At the same time, we refer to A. Salam [3] , as he is the one of the first who drew attention to the discrepancy between the quantum level of the numerical value and the Newtonian gravitational constant. It is he who proposed the concept of “strong” gravity, which was based on the assumption of the existence of f-mesons of spin-2 generating SU (3) multiplet (described by Pauli-Fierz equation). It is shown that the possibility of another link constant along with the Newtonian is not inconsistent with the observed effects [3] . This approach was not further developed due to a number of reasons. It is clear now that the numerical value of the “strong” gravity constant should be used in Equation (1) with
, where G is the Newton’s gravitational constant. Equation with certain constants determined in this way is the equations of the Einstein’s theory of general relativity. Equation (1) is a common mathematical form of the gravitational field equations corresponding to the principle of equivalence and the postulate of general covariance. The equations of the form (1) are obtained simultaneously by Einstein and independently by Gilbert [2] . At the same time, we refer to A. Salam [3] , as he is the one of the first who drew attention to the discrepancy between the quantum level of the numerical value and the Newtonian gravitational constant. It is he who proposed the concept of “strong” gravity, which was based on the assumption of the existence of f-mesons of spin-2 generating SU (3) multiplet (described by Pauli-Fierz equation). It is shown that the possibility of another link constant along with the Newtonian is not inconsistent with the observed effects [3] . This approach was not further developed due to a number of reasons. It is clear now that the numerical value of the “strong” gravity constant should be used in Equation (1) with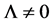 . By the way, when
. By the way, when 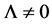 there are stationary solutions of general Einstein’s equations as it was stated by Einstein himself, but after the discovery of non-sta- tionary solutions with
there are stationary solutions of general Einstein’s equations as it was stated by Einstein himself, but after the discovery of non-sta- tionary solutions with 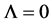 by A. Friedman [4] , finally the general theory of relativity was formed as it is now known. The decisive argument in general relativity for equating
by A. Friedman [4] , finally the general theory of relativity was formed as it is now known. The decisive argument in general relativity for equating 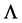 -member to zero is the need to correct limiting transition to Newton’s theory of gravitation.
-member to zero is the need to correct limiting transition to Newton’s theory of gravitation.
2. Mathematical Model
Starting from the 70 s it became evident [3] that in the quantum domain numerical value of G is not compatible with the principles of quantum mechanics. A number of studies [3] have shown that in the quantum domain acceptable is constant K, wherein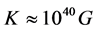 . This marked the problem of generalization of the relativistic equations for the quantum level: this generalization should join the numerical values of the constants in quantum and classical fields.
. This marked the problem of generalization of the relativistic equations for the quantum level: this generalization should join the numerical values of the constants in quantum and classical fields.
In the development of these results as an approximation to the micro level of the field equations of Einstein, a model based on the following assumptions is proposed:
The gravitational field in the region of localization of elementary particles with mass m0 is characterized by the values of the gravitational constant K and constant Λ, which lead to the stationary states of a particle in its own gravitational field, and stationary states of the particles themselves are the source of the gravitational field with the Newtonian gravitational constant G.
The complexity of solving this problem forced to turn to the simplest approximation, namely the calculation of the energy spectrum only in the approximation of the fine structure due to relativism
The problem on the stationary states of an elementary source in its own gravitational field is reduced to the solution of the eigenvalue problem 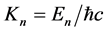 and eigenfunctions of the radial wave function f (describing the states with definite energy E and orbital moment l: indices El are omitted) of boundary value problem:
and eigenfunctions of the radial wave function f (describing the states with definite energy E and orbital moment l: indices El are omitted) of boundary value problem:
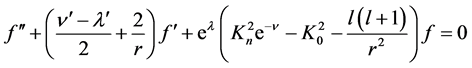 (2)
(2)
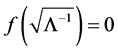 Left bound (3)
Left bound (3)
 Right bound (4)
Right bound (4)
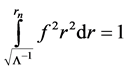 Normalization requirement (5)
Normalization requirement (5)
Equation (2) is complemented by the equations:
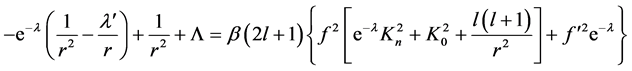 (6)
(6)
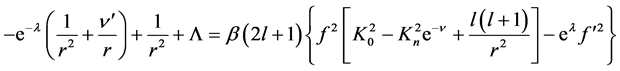 (7)
(7)
With boundary conditions


Scalar curvature R in the condition (8) is given by the same expression that is written in the left side of the condition (9).
Equations (2) and (6)-(7) follow from Equations (10)-(11)


after the substitution of 

tions in the central-symmetry field metric with the interval defined by the expression [5]

Above indicated: 





Right-hand sides of Equations (6)-(7) are calculated from the general expression for the energy-momentum tensor of a complex scalar field:

The respective components Tmn are obtained summing by index m using specific identities for the spherical
functions [6] after the substitution in (13)
3. Energy Spectrum
In the simplest (in terms of initial mathematical evaluations) approximation, the problem for stationary states in its gravitational field (with the constants K and
1) If the numerical values of K ≈ 5.1 × 1031 N∙m2∙kg−2 and L = 4.4 × 1029 m−2, there is a spectrum of stationary states of the electron in its own gravitational field (0.511 MeV ∙∙∙ 0.681 MeV). The main state is the observed electron rest energy 0.511 MeV. This numerical value of L has important physical meaning: an introduction to the Lagrangian density permanent member, not dependent on the state of the field. This implies the existence of irremovable space-time curvature, not affiliated with any matter, nor with the gravitational field.
2) These steady states are the sources of the gravitational field with constant G.
3) Transitions between the stationary states of the electron in its own gravitational field lead to gravitational radiation, which is characterized by a constant K that gravitational radiation is the emission of the same level as electromagnetic (electric charge e, gravitational charge )
where Qij is a quadrupole moment tensor of the mass distribution of the radiating system, and the constant in this relationship defines the order of magnitude of the radiation power. Wrongfulness of this formula, as follows from the above, is not to use the quadrupole approximation, but in the scheme calculation. The presence of stationary states in the own gravitational field allows the correct calculation of gravitational radiation in the strict quantum approach based on the spectrum of transitions to stationary states already with constant K. It is permissible to use not only quadrupole, but also dipole quantum approach, which is quite obvious. Gravitational waves with the constant G do not exist. That is evidenced by the negative results of the detection of gravitational waves, based on the assumption of a completely illegitimate assumption of gravitational wave generation by any mass distribution with variable multipole (starting with quadrupole) moments.
4) The presence of the stationary states of the electron in its own gravitational field is in full compliance with the special theory of relativity. According to STR, relativistic relation between energy and momentum is broken, if we assume that the total energy of the electron is determined only by the Lorentz electromagnetic energy [8] .
This means that the total energy of an electron at rest is 4/3 of its Lorentz electromagnetic energy. That corresponds to the numerical data on the spectrum of stationary states of the electron in its own gravitational field. In the Standard Model the relativistic relation between the energy and momentum of the electron is broken, as it is assumed that the total energy of the electron is determined only by the Lorentz electromagnetic energy. This follows from the fact that the gravitational interaction at the quantum level in the Standard Model is not considered.
It should immediately be noted that the numerical evaluation of the spectrum is approximate. The greatest uncertainty is the estimation of the numerical value of the first steady state, as more and more accurate as you approach
5) Estimate of the numerical value of K can be obtained with the help of Kerr-Newman metric using the following formula:

where r, m, e, L, c are the classical electron radius, mass, charge, orbital angular momentum, the speed of light, correspondingly. The numerical value of the orbital angular momentum was taken equal to the spin of the electron.
Thus, we can assume that the physical nature of spin is possible that this value is the orbital angular momentum of the particles in their own gravitational field. This gives ground to consider that the use of Klein-Gordon equation is not so easy.
The distance at which the gravitational field with the constant К is localized is less than the Compton wavelength, and for the electron, for example, this value is of the order of its classical radius. At distances larger than this one, the gravitational field is characterized by the constant G, i.e., correct transition to Classical GR holds.
Cite this paper
Stanislav Fisenko, (2016) The Problem on Stationary States in Self Gravitational Field. Journal of Modern Physics,07,1045-1048. doi: 10.4236/jmp.2016.710093
References
- 1. Fisenko, S.I. and Fisenko, I.S. (2015) Journal of Physics: Conference Series, 574, 012157.
http://dx.doi.org/10.1088/1742-6596/574/1/012157 - 2. Hilbert, D. (1915) Grundlagen der Physik, 1 Mitt. Gött. Nachr., 1915, math.-nat. Kl., S. 395.
- 3. Siravam, C. and Sinha, K. (1979) Physics Reports, 51, 112-123.
- 4. Friedmann, A. (1922) Zeitschrift für Physik, 10, 377-386.
http://dx.doi.org/10.1007/BF01332580 - 5. Landau, L.D. and Lifshitz, E.M. (1976) Field Theory. Publishing House 《Nauka》, Moscow.
- 6. Warshalovich, D.A., et al. (1975) Quantum Theory of Angular Momentum. Publishing House 《Nauka》, Leningrad, 282-285.
- 7. Fisenko, S.I. and Fisenko, I.S. (2009) The Old and New Concepts of Physics, 6, 495-452.
- 8. Pauli, W. (1958) Theory of Relativity. Pergamon Press, Oxford.


