Received 18 April 2016; accepted 25 April 2016; published 28 April 2016

ABSTRACT

The paper suggests that quantum relativistic gravity (QRG) is basically a higher dimensionality (HD) simulating relativity and non-classical effects plus a fractal Cantorian spacetime geometry (FG) simulating quantum mechanics. This more than just a conceptual equation is illustrated by integer approximation and an exact solution of the dark energy density behind cosmic expansion.

Keywords:

Fractal Cantorian Spacetime, Quantum Relativity, Superstrings, Transfinite Set Theory, Extra Spacetime Dimensions, Quantum Physics, Dark Energy, Accelerated Cosmic Expansion, Cosmic Topology, Hyperbolic Geometry, E-Infinity Theory, Post Modernistic Physics

1. Introduction

Post modernistic research in theoretical physics [1] - [20] notably that connected to superstrings [21] - [25] , loop quantum gravity [26] [27] , fractal-Cantorian spacetime [28] - [30] , M-theory [24] [30] [31] and a host of other theories [1] [2] [17] - [19] is most if not all pointing towards a rather firm fact that higher dimensionality and fractal geometry can be used to simulate relativity as well as quantum mechanics and possibly replace them, at least partially and at a minimum in basic situations where relativity and quantum mechanics are both relevant in equal measure [1] - [4] [32] [33] . Looking a little back in history, this is actually the achievement of visionaries and a few towering figures of science which are not credited sufficiently with pointing to what in our opinion is the superior direction of geometrizing and “topologizing” physics and cosmology in a most general way [1] [2] [15] such as F. Gauss [3] , J. Bolya, N. Lobachevsky, H. Minkowski [3] , J. von Neumann and A. Connes [34] . All apart from these pioneers, the recent contributions to the theory of fractal spacetime and the E-infinity theory of G. Ord, L. Nottale and the present author are almost exclusively going in the same direction constituting the subject of the paper at hand [4] [6] [8] .

In the present work which is anticipating a sweeping new revolution in the way, we will be doing physics in 10 to 20 years, [1] - [54] , we will illustrate the above by giving in a relatively short and concentrated form various, and on its face value, classical derivations of the fundamental major problem of the supposedly “missing” dark energy density of the cosmos amounting to 95.5 to 96 percent of the total theoretically expected value [33] - [36] .

To keep the length of the present paper to a minimum we start from what we called in a recent paper [37] “The real Einstein” beauty E = kmc² where k is essentially related to the familiar Lorentzian factor 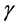with a twist. Thus in the present paper we introduce 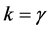as being the topological energy density factor of a generalization of Einstein’s famous equation [1] [38] [39]

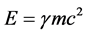(1)

where E is the energy, m is the mass and c is the speed of light while 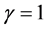is evidently related to the absolute maximal energy density possible E = mc² [40] . The deep meaning of the above as well as the controversial aspect connected to rest mass, real mass conversion to energy, difference and similarity to Newton kinetic energy E(k) = (1/2)mv² where v is the classical velocity of a particle as well as Einstein’s leap to a fully fledged generalization of similar earlier discoveries of E = mc² by Poincare and others will not be discussed here in the depth it requires [35] - [39] . Instead to cover these fundamental aspects, the reader is advised to consult first the outstanding work of Prof. W. Rindler and Prof. L.B. Okun [40] [41] and second the earlier work of the present author and the references cited therein [35] - [39] .

2. A More than Noteworthy Hidden Connection between Riemann’s Powerful Curvature Tensor [42] - [44] and I. Dvoretzky’s Magnificent Theorem Regarding Measure Concentration [45] - [48]

We are invoking here nothing connected directly to the theory of relativity or quantum mechanics and yet we will arrive to a result which can be understood deeply only via these two pillars of modern physics [1] [3] [4] . The main idea behind the following analysis of dark energy is the intuitive picture that extra dimensions are where things can be there but not directly seen nor in fact measured by us 3-dimensional beings and with time being only a parameter not given to us in a tangible, physical way let alone the fifth dimension of Kaluza and Klein nor Witten’s eleven dimensional spacetime of his M-theory which is way above our non-mathematical intuitive grasp. Confining ourselves to n dimensional Riemannian tensor R⁽ⁿ⁾ one could take the view with considerable justification, that R⁽⁵⁾, i.e. five dimensions is about the limit of accessible physics in the experimental possibilities of a 3 + 1 dimensional conscious and well equipped observer. At the same time it is an educated guess that M-theory is real and R⁽¹¹⁾ is probably one of the best ways to describe not only theoretical high energy physics but the entire cosmos. To put this to a pragmatic test we calculate the vital independent components of the most important driving force in Einstein’s relativity, namely the Riemann tensor. For n dimensions this number is given by [42] - [44] [54]

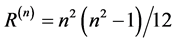(2)

Setting n = 5 and n = 11 one finds [54]

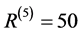(3)

and

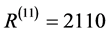(4)

respectively. Assuming that all these components have almost the same statistical weight, then the difference between 50 and 2110 measures clearly the sparseness of the associated space and consequently the totality of the average curvature. Similarly the ratio between 50 and 2110 is a measure of the density of the energy which is likened in the theory of relativity mainly to the curvature as it is in the case a simple elastic wire in the theory of engineering elasticity. Viewing the complex problem in this quite simplistic way leads us directly to estimating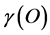, i.e. the density of the probably accessible energy which we can normally measure directly and call it aptly and logically, ordinary energy as follows [42] - [44] [54] :

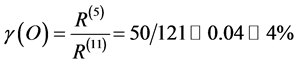(5)

Consequently the rest of the energy filling not only D = 5 but also D = 11 must be given by the so called dark energy density which is given logically by [35] - [39]

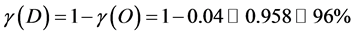(6)

For two important reasons the preceding rough result is truly striking. First it is quite close, in fact very close to highly accurate cosmic measurements and observations connected to the famous COBE, WMAP and Type 1a Supernova [33] [39] which was awarded the Nobel Prize in Physics or Cosmology in 2011. These measurements establish the existence of 4.5% ordinary energy density while the expected but missing 95.5% energy density was dubbed dark energy and concluded that it is behind the accelerated rather than previously believed deceleration of cosmic expansion [33] [39] . The second reason for the profundity of our simple estimation is connected to the magnificent theorem of the late, great Ukrainian born legendary mathematician and past President of the Wiseman Institute, I. Dvoretzky [45] - [48] . This theorem states that in a high dimensional manifold almost 96 percent of the volume is at the surface leaving only 4 percent in the bulk. The analogy and connection is obvious. Now we have solved this problem in numerous previous publications and came to a definite answer, namely that E of Einstein may be dissected into two quantum components E(O) of the quantum particle and E(D) of the quantum wave. Within an exact integer solution one finds that [35] - [39]

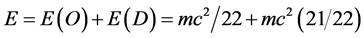(7)

That means E(O) is not 4% but rather 4.5% while E(D) is not 96% but 95.5% to a very high degree of accuracy and in astounding agreement with measurements [33] [30] . This leads us to the next section where we will attempt to improve our first estimation presented at the beginning of this section.

3. An Almost Exact Integer Solution of the Ordinary and Dark Energy Density Problem Based on the Number of Independent Riemannian Curvature

Our first estimate of clearly missed the fact that we needed to add D = 5 to R⁽⁵⁾ = 50 and analogously D = 11 to R⁽¹¹⁾ = 1210. This is an obvious and trivial embedding problem because R⁽⁵⁾ and R⁽¹¹⁾ are treated as quasi-dimensions estimating the size of our spacetime manifold. Consequently a more accuret 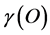must be [35] - [39] [45] - [48]

(8)

This is almost the familiar exact rational (1/22) value as document in my previous papers using different methods. Clearly 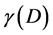is given by the self explanatory values

(9)

almost exactly as expected.

4. The Exact Integer Value of Ordinary and Dark Energy Density

Although not trivial, it is not difficult to obtain the truly exact formulas of energy density and using the Riemannian tensor independent components method. The trick is to realize that we have to add not D⁽⁵⁾ = 5 to R⁽⁵⁾ but the full space which embeds the SL(2, 7) Lie symmetry group of the holographic boundary of our universe, i.e. D = 7 and similarly the vacuum of Witten’s D = 11 which is the corresponding pure gravity with. For n = 8 we have the famous D = 20 case but in the case of eleven dimensions we set n = 11 and find a 44 degrees of freedom vacuum. Consequently our exact must be given by [35] - [39] [45] - [48] .

(10)

In other words we have [35] - [38] [52]

(11)

which is this time the truly exact integer value. For we have naturally also the exact integer value

(12)

We may remark on passing that 57 is actually the intrinsic dimension of the fundamental E(8) exceptional group [52] with its famous 248 isometries which gives E8E8 of D. Gross et al. heterotic superstring symmetry group, the famous |E8E8| = (2) (248) = 496 dimensions [50] - [52] .

5. A Short Introduction to the Von Neumann-Connes Theory and Comparison with the Exact “Transfinite” Solution of Ordinary Dark Energy Density

Readers familiar with E-infinity Cantor spacetime theory [4] [8] know that the key to all exact results of this theory, including the ordinary and the dark energy density section of the cosmos, is the deceptively simple dimensional function due to the work of J. von Neumann in his unsung papers and book published posthumously “Continuous Geometry” as well as the work of the creator of noncommutative geometry, the great French pure and applied mathematician A. Connes [34] . This function as is well known is given by [34]

(13)

where is the Hausdorff dimension, and. In E-infinity we made our first move by identifying the zero set as being necessarily be the empty set which we equate physically and mathematically to the pre-quantum wave. Therefore the Hausdorff dimension of the empty set is given by and can be found together with all other sets recursively in a Fibonacci-like way as shown below where we start with the two trivial seeds, namely the zero set and the unity set which are indicated in Equation (14) by two small arrows. Proceeding in this way we find [34] [39]

(14)

From the above we see that the pre-quantum particle is identified by the bi-dimension [47]

(15)

while the pre-quantum wave is given by

(16)

From all these previous results, it is easily reasoned that the “topological” volume of the pre-particle in 5D is given by the obvious multiplication formula [39]

(17)

The corresponding additive volume of the pre-quantum wave on the other hand is given by

(18)

The total volume is thus equivalent to world sheet of string theory [21] - [25]

(19)

Inserting mean volume = 2/2 = 1 in Einstein’s formula E = mc² one finds [35] - [39]

(20)

That means [35] - [39] [48] - [52]

(21)

This is the exact expression which leads to the integer solution by disregarding k = 0.18033989 compared to 21 and 22. We note that this k was interpreted physically as ‘tHooft’s renormalon hypothetical particle which is equal to where is hardy’s famous quantum probability of two entangled quantum particles which is the exact solution of the corresponding Dirac’s equations of the problem. In addition we must stress that was verified experimentally and found to a very high degree of precision. Thus our theory is well founded theoretically and experimentally on all fundamental levels. The more interesting it must be that one can find the exact integer solution without direct reference to the theory of quantum relativity. In the next section we will look at the same problem using nothing more than our ordinary three dimensional space coupled to a rather familiar fractal curve [53] .

6. Solving Dark Energy in a Classical Newtonian Three Space Dimensions

Although we have not invoked in all the preceding analysis any Lorentzian transformations or Einsteinian conception relating to the meaning of simultaneousity [40] nor of course a Schrödinger equations [1] - [9] , we did make extensive use of higher dimensionality of spacetime as well as the basic final results of Einstein’s special relativity marvel, namely E = mc². In the following solution all these things will be dispensed of so that the reader may see clearly the main message of the present paper that even a low dimensional fractal is essentially infinite quasi dimensional because of the involved infinite iteration and self similarity and that even a harmless conventional fractal curve in 3 dimensions like the familiar Menger sponge [53] could simulate quantum effects involved in the physics geometry and topology of ordinary and dark energy density of the cosmos [47] - [57] . Thus we draw in our following analysis on the classical three dimensional sponge named after the great Austria- American mathematician Karl Menger [53] who together with the outstanding young Russian mathematician P. Urysohn discovered the inductive dimensional theory which is one of our main tools in erecting E-infinity theory [28] [50] . The Hausdorff dimension in this case is [53]

(22)

This fractal, although it looks like a cubic sponge in 3D is essentially a curve, not a real 3D and possesses in our case the disadvantage of being continuous and could therefore be expected to deliver a good approximation only because continuity violates one of our main E-infinity theory principles, namely being the “pointless” point-set theory as emphasized in the pioneering work of von Neumann’s continuous geometry where continuity is not referring to the geometry [34] [39] [47] but to the spectrum of the most important topological invariant of a manifold, namely the dimension. Thus one should not be misled by the word “continuity” with which von Neumann means fractal dimensionality spectrum but at the time, the word fractal was not invented yet by Mandelbrot nor were fractals part of the mathematical science culture [3] [46] . Since the Hausdorff dimension refers here not to the dark non-differentiable lines remaining from the Menger sponge iteration but to the space encased between these 3 dimensional lines, we see that the ratio between D_H = 2.726833028 and D_T = 3 will give us the density of the involved empty set which represents dark energy. Consequently we may write

(23)

Consequently the ordinary energy density must be

(24)

Now, and this is a crucial point, we do not insert in Einstein’s formula which we used all along because Einstein’s formula belongs to D = 4 while the previous analysis is in D = 3. Here we remain truly classical and insert in of Newton and take the limit to find

(25)

For a basically almost entirely classical analysis this result reinforces our conjectured equation:

(26)

and together with the rest of the paper shows beyond reasonable doubt that there is far more than meets the eye to dimensionality of spacetime and fractal Cantorian geometry.

7. Discussion and Conclusion

There are many shortcut derivations and radically different solutions all converging directly or indirectly towards the main thesis of the present work, namely that of measure concentration of volume in a sufficiently high dimensional manifold with fractal-Cantorian features. Thus, we have all three fractal spacetime theories of ‘tHooft-Veltman-Wilson dimensional regularization spacetime D = 4 − k as well as Kaluza-Klein fractal space and Witten’s fractal M-theory [55] with the remarkable dimensionality all leading to exactly the same result, namely [35] - [39]

(27)

where. The “integer” exact value is

(28)

The analysis is in complete conformity with the result based on pure mathematical theorems such as Dvoretzky’s theorem as well as accurate measurements and observations such as COBE, WMAP and Type 1a supernova which is awarded the 2011 Nobel Prize [35] - [39] .

From all the above we conclude that higher dimensionality and fractality of spacetime are a reality of the small and large scale structure of spacetime and that our conceptual equation constituting the title of the present paper is far from being esoteric or mathematical abstraction with no tangible content. Hardy’s quantum entanglement [35] - [39] , the missing dark energy which we find and the observed accelerated cosmic expansion clearly says that our conceptual equation is real. From this fundamental conclusion to the realization that negative probability, phantoms and ghosts in strings and quantum fields are fairly exchangeable concepts lurking behind the empty set dark energy of the quantum wave is only one step [57] .

Cite this paper

Mohamed S. El Naschie, (2016) On a Quantum Gravity Fractal Spacetime Equation: QRG ≃ HD + FG and Its Application to Dark Energy—Accelerated Cosmic Expansion. Journal of Modern Physics,07,729-736. doi: 10.4236/jmp.2016.78069

References