Received 8 April 2016; accepted 10 May 2016; published 13 May 2016

ABSTRACT

A force with an acceleration that is equal to multiples greater than the speed of light per unit time is exerted on a cloud of charged particles. The particles are resultantly accelerated to within an infinitesimal fraction of the speed of light. As the force or acceleration increases, the particles’ velocity asymptotically approaches but never achieves the speed of light obeying relativity. The asymptotic increase in the particles’ velocity toward the speed of light as acceleration increasingly surpasses the speed of light per unit time does not compensate for the momentum value produced on the particles at sub-light velocities. Hence, the particles’ inertial mass value must increase as acceleration increases. This increase in the particles’ inertial mass as the particles are accelerated produce a gravitational field which is believed to occur in the oscillation of quarks achieving velocities close to the speed of light. The increased inertial mass of the density of accelerated charged particles becomes the source mass (or Big “M”) in Newton’s equation for gravitational force. This implies that a space-time curve is generated by the accelerated particles. Thus, it is shown that the acceleration number (or multiple of the speed of light greater than 1 per unit of time) and the number of charged particles in the cloud density are surjectively mapped to points on a differential manifold or space-time curved surface. Two aspects of Einstein’s field equations are used to describe the correspondence between the gravitational field produced by the accelerated particles and the resultant space-time curve. The two aspects are the Schwarzchild metric and the stress energy tensor. Lastly, the possibility of producing a sufficient acceleration or electromagnetic force on the charged particles to produce a gravitational field is shown through the Lorentz force equation. Moreover, it is shown that a sufficient voltage can be generated to produce an acceleration/force on the particles that is multiples greater than the speed of light per unit time thereby generating gravity.

Keywords:

Charged Particles, Accelerated Particles, Inertial Mass, Gravitational Force, Einstein’s Field Equations, Space-Time Manifold, Schwardchild Metric, Stress Energy Tensor, Surjective Mapping, Lorentz Force

1. Introduction

It has been shown that a gravitational field can be generated by the oscillation of a quark in a paper written by author Eli Peter Manor published in 2016 in the Journal of Modern physics [1] . While oscillating, the quark would achieve velocities that near the speed of light; the inertial mass of the particle would increase resultantly generating a gravitational field [1] . The aim of this paper is to show that a gravitational field can also be produced as the inertial mass of a charged particle increases when accelerated to the verge of the speed of light via an electromagnetic field (as in a particle accelerators). Moreover, a description of the space-time curve associated with the gravitational field generated will be mathematically formulated.

In describing the assertion of this paper in more detail; a gravitational field is generated when a cloud of charged particles is accelerated to the precipice of the speed of light. The acceleration enacted on the particles exceed the speed of light per unit time, however massive particles cannot exceed the speed of light as is well known. Resultantly, as the acceleration increasingly exceeds the speed of light per unit time, the particles’ velocities approaches but never achieves a luminous velocity. Mathematically, the particles’ velocities asymptotically approaching the speed of light will not compensate for the amount of force or acceleration exerted on the particles; the inertial mass value of each particle must increase to compensate for the increasing acceleration or force. In this assertion, each charged particles’ velocity is approximated to a constant 99% of the speed of light (), allowing the measurement of increased inertial particle mass. Consider Newtonian gravitational force as shown below [2] .

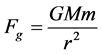
All mass values correspond to a density value; even if the unit volume is infinitesimally small. The sum total of increasing individual inertial mass values of each particle in the density of accelerated particles is set equal to source mass M in the gravitational force 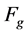as the acceleration on the charged particles increase. Hence, as the force acting on the particles increase with an invariant approximate velocity of 99% the speed of light; the corresponding force of gravity increases proportionally. This implies that a curvature in space-time is also generated by the cloud of accelerated charged particles. Therefore, Einstein’s field equations are used to describe the curvature in space-time generated by the accelerated charged particles. It will be shown that there exist a surjective or “onto” map from the Cartesian product of the particles acceleration number (or the multiples of acceleration past the speed of light per unit time) and the number of particles in the cloud density to the codomain of points and displacements on a space-time manifold. Two descriptions using Einstein’s field equation are shown to correlate to the surjective mapping from the domain of the particle acceleration number and the number of particles to the codomain of points or displacements on the space-time curve produced by the accelerated cloud. The first description is the Schwarzchild metric description and the second is the stress-energy tensor description. Lastly, the electromagnetic force or Lorentz force equation is used to show that it is possible to obtain a sufficient voltage to accelerate a cloud of charged particles to a velocity that is an infinitesimal fraction below the speed of light to produce a gravitational field and/or space-time curve.

2. Acceleration of Charged Particles and Newtonian Gravitation

In using electromagnetic force or Lorentz force to accelerate the cloud of charged particles, acceleration 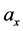is generated. Acceleration 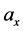is 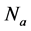multiples of the speed of light c per unit time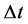, where is any real number that is greater than or equal to one. Number 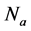will be referred to as the acceleration number.

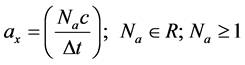(1.0)

Acceleration corresponds to the force 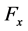per area 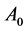acting on the cloud of accelerated charged particles, which correspond to pressure 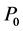(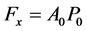) [2] . Area is also the cross sectional area traversed by the charged particles. The force can be expressed in terms of Newton’s second law such that [2] :

(1.01)

The momentum value is conventionally obtained by integrating force in respect to time t with limits of integration from zero to time as shown below [2] .

(1.02)

Keep in mind that momentum value corresponds to the relativistic energy value of; where the particles’ mass value in energy E is treated as rest mass due to the fact that the charged particles are massive particles and not relativistic particles such as photons [2] . Acceleration number varies proportionally to force. Thus momentum corresponds to force, however it is well understood that the charged particles of inertial mass cannot obtain super luminous velocities, therefore the particles’ approximate momentum will be denoted as shown in Equation (1.03) below.

(1.03)

As acceleration increases, the particles’ velocity asymptotically approach but never achieve the speed of light; to circumvent this infinite decimal expansion, the asymptotic increase is set equal to the constant approximate of velocity denoted. Velocity is the particles’ approximate velocity “close to” but less than the speed of light as shown by Equation (1.04). Velocity is approximated to 99 percent of the speed of light for the purposes of this formulation.

(1.04)

Mass value corresponding to momentum is referred to as variable inertial mass. Variable inertial mass takes on values greater than or equal to inertial mass.

(1.05)

To avoid confusion, it must be noted that relativistic mass dilation is different from the variation of variable mass or inertial as the particle approaches the speed of light. This can be conveyed by setting variable inertial mass equal to the product of the variable inertial mass and the Lorentz factor as shown below [2] .

(1.06)

This can alternatively be expressed such that [2] :

(1.07)

Equation (1.06) implies that the Lorentz factor is equal to 1 and implies that relative velocity v or the velocity of an observer is zero () for the purpose of this derivation.

(1.08)

Thus inertial mass does not vary according to the Lorentz factor. Conclusively, relativistic mass is dependent on the velocity and orientation of an observer while the inertial varies according to momentum. In continuing the formulation, momentum value is set equal to momentum.

(1.09)

This equivalence can be expressed as:

(1.10)

Equation (1.10) represents an important aspect of the assertion. The charged particles of the accelerated mass cannot exceed the speed of light, thus, variable inertial mass must vary proportionally to the acceleration number; where the values c, , and are constant. At this juncture, one solves for variable inertial mass. Variable inertial mass is such that:

(1.11)

Equation (1.11) can be expressed such that:

(1.12)

The premise of the assertion is the correlation of the acceleration of a cloud of charged particles and gravitation, therefore Newtonian gravitational force is given such that [2] :

(1.13)

The density of the accelerated cloud of charged particles is denoted where is the discrete number of charged particles in the cloud per unit volume (V) as displayed below.

(1.14)

This implies that:

(1.15)

where M is the source mass in gravitational force. In the task of defining gravitation in terms of the varying inertial mass associated with the accelerated cloud of charged particles, again, consider Newtonian gravitational force [2] .

(1.16)

where are the spatial coordinates in (), mass M in Equation (1.16) (or Newtonian gravitational force) is substituted according to expression 1.15 (). Newtonian gravitational force can then be expressed such that:

(1.17)

Mass value is the mass of the particle at distance under the influence of the gravitational force produced by the cloud of accelerated charged particles. Substituting the value of inertial mass into Equation (1.17); gravitational force can then be expressed such that:

(1.18)

Therefore, the accelerating force acting on the charged particles is oriented in the direction of travel while the force of gravity generated by the particles is orthogonal to the direction of travel and therefore force. Section 2 will introduce the correlation of the gravitational space-time curve associated with the gravitational field generated by the accelerated charged particles.

3. Gravitation Produced by Accelerated Charged Particles and Einstein’s Field Equations

The gravitational field generated by the cloud of accelerated particles on the verge of the speed of light inherently produces a space-time curve. Therefore the mathematical description of the space-time curve produced by the accelerated charged particles is given by Einstein’s field equation. Consider the function of expression (2.0) below.

(2.0)

The function is a surjective or “onto” map from the domain composed of the Cartesian product to the codomain of n-dimensional real numbers [3] . Map has a domain of the number of charged particles in the density of the cloud of accelerated particles which is an element of natural numbers () and the acceleration number which is an element of real numbers (). Map is expressed as shown below [3] .

(2.01)

The symbol denotes the field function to which the space-time curve or manifold is defined [3] . In more technical terms, the field represents the differential manifold to which the metric tensor is defined on [4] . Thus function is a map from the set of Minkowski coordinates [4] in set () to the codomain of the set of points and displacements in set () which is the set of points and displacements on the n-dimensional differential manifold or space-time curve surface. Where () is a partial derivative operator in respect to, the function is a map such that [3] :

(2.02)

The equivalence of function and function imply a composition of functions . Thus, Equation (2.0) expresses the composition map such that:

(2.03)

Thus, for every value and in the domain of map there exist a value a () such that a is an element of set (), hence the “onto” or surjective mapping. Expression 2.0 is the correspondence of the number of particles and acceleration number to solutions of Einstein’s field equation which are defined on a space-time manifold or set. It will now be shown that the function of correspond to given solutions of the Einstein Field equations. Let function equal a value such that:

(2.04)

where A and B are arbitrary values, is the metric tensor, and is an element of the set of values on the n-dimensional differential manifold . The Einstein tensor is set equal function such that [3] :

(2.05)

The Einstein tensor is given such that [3] :

(2.06)

[where is the Ricci tensor, R is the scalar constant, and is the differential commutator for computing curvature [3] . This implies that the values of A and B in are such that:

, (2.07)

As a second example, function is now set equal to the stress-energy tensor for a perfect fluid as shown below.

(2.08)

The Stress-energy tensor is given such that [3] :

(2.09)

[where is the Lagrangian for the Klein-Gordon equation [3] ] This implies that the values of A and B in are such that:

, (2.10)

Due to the equivalence of function and function or; this Implies that [3] :

; (2.11)

Therefore the components of the Einstein tensor and the stress-energy tensor reside in the codomain of function. This paper presents two derivations of Einstein’s field equations that express the equivalence of the functions. Therefore, there are two descriptions of the space-time curve generated by the cloud of accelerated charged particles using two separate aspects of Einstein’s field equations. The first description is the Schwarzchild aspect and the second is the stress-energy aspect as will be formulated in the next section.

4. The Schwarzchild and Stress-Energy Description of a Space-Time Curve Generated by a Cloud of Accelerated Particles

Section 3 will introduce two formulations linking the number of particles and acceleration number to solutions to Einstein’s field equations, hence, validating the equivalence of. The formulation begins with the Schwarzchild description.

The Schwarzchild descritption

In reference to this hypothetical description, accelerated charged particles traveling at velocities bordering the speed of light generate a gravitational field on a spherically symmetric body, hence, the need to formulate a description using the Schwarzchild metric. The Schwarzchild radius is given such that [3] :

(3.0)

Gravitational force of Equation (1.18) is expressed in terms of the Schwarzchild radius as shown below.

(3.01)

Gravitational potential energy is conventionally obtained by evaluating the integral in respect to Schwarzchild radius giving a value such that [3] :

(3.02)

The maximum value of kinetic energy for a particle of mass in the fluid with a maximum velocity at the speed of light c is given such that [2] :

(3.03)

As is conventionally performed, kinetic energy is set equal to gravitational potential energy as shown below [2] .

(3.04)

This equivalence can be expressed as [2] :

(3.05)

Solving for the Schwarzchild radius gives the radius in terms of the number of particles and acceleration number as shown below [2] .

(3.06)

The Schwarzchild metric is given such that [3] :

(3.07)

The functions and take on values of the Schwarzchild radius such that [3] :

(3.08)

(3.09)

[where r is the radius of the spherically symmetric body [3] ] The prime notation (') denotes that the variations in the metric correspond to the number of particles and acceleration number. The metric is set equal to the metric tensor.

(3.10)

Expressing the value of metric tensor gives the matrix expression of:

(3.11)

Therefore, the Einstein tensor can be expressed such that [3] :

(3.12)

where the Ricci tensor is expressed in terms of the differential commutator for computing curvature such that [3] :

(3.13)

The requirement of the equivalence of () is satisfied where function is substituted by function at time t, spherical radius r, and spherical angles and indicating the spherical coordinates of the Schwarzchild metric.

(3.14)

The stress-energy tensor description

A cloud of charged particles are again accelerated via an electromagnetic force (of any given source i.e. particle accelerator or subatomic charged particles emitted from a star) to the verge of the speed of light producing a gravitational field that is exerting on a fluid of particles of mass per unit volume. For the purpose of this derivation, the fluid is considered a perfect fluid. Thus, the stress energy tensor for a perfect fluid is expressed as shown below [3] .

(3.15)

where is the Lagrangian for the Klein-Gordon equation as shown below [3] .

(3.16)

The fluid 4-velocity denoted varies along a geodesic embedded on the space-time manifold. Fluid velocity progresses along a time-like curve and can be expressed in terms of the chain rule [5] as expressed below [3] .

(3.17)

The geodesic rule is acknowledged as shown below [3] .

(3.18)

Hence the appropriate use of the Christoffel symbol applies as follows [3] .

(3.19)

In substituting fluid velocity for the differential notation of in Equation (3.15), the stress-energy tensor is expressed such that [3] :

(3.20)

Consider dynamic pressure at fluid velocity and fluid density shown below.

(3.21)

At this juncture, fluid velocity is substituted with the time-like partial derivative in dynamic pressure as shown below [2] .

(3.22)

Or alternatively,

(3.23)

Let dynamic pressure equal the expression of the sums of components of partial pressure, where each component of pressure is a part of the diagonal components of the 4 by 4 matrix of stress-energy tensor .

(3.24)

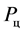
This implies that:

(3.25)

Isolating the partial derivatives, gives:

(3.26)

Substituting Equation (3.26) into Equation (3.20) (or the stress tensor), one obtains:

(3.27)

Consider the unit vector u in shown below [5] .

(3.28)

Gravitational force generated by accelerated particles is multiplied by unit vector giving a vector valued force [5] .

(3.29)

Using the classical equation of pressure equal to force per unit area () [2] , components of pressure is set equal to the components of the ratio of vector valued gravitational force and spherically symmetric area () perpendicular to force as shown below.

(3.30)

The sums of components of pressure are equal to the sums of components such that:

(3.31)

Substituting the value of Equation (3.31) into Equation (3.27) gives the stress energy tensor such that:

(3.32)

The stress energy tensor is set equal to the Einstein tensor () to show the correspondence between the gravitational stress T () exerted on a perfect fluid which flows through a region of space-time and the curved geometry of that region of space-time to which the fluid travels. Thus, Equation (3.32) below gives a full description of the gravitational effects of the cloud of accelerated charged particles on both the dynamics of the fluid and the curved surface of the space-time maniflold.

(3.32)

Conclusively, the stress-energy tensor describing the pressure exerted by the gravitational field produced by the accelerated charged particles on a perfect fluid correspond to the surjective map of (or). Therefore it has been effectively shown to correlate the variations in the number of particles and acceleration number to solutions to Einstein’s field equation.

5. The Generation of Electromagnetic Force to Exert Sufficient Acceleration to Produce a Gravitational Field

It is of great importance to show the possibility and feasibility of accelerating a cloud of charged particles to an extent to where they actually produce a gravitational field in the real world. Thus, the Lorentz equation of electromagnetic force is applied to show this possibility. Lorentz force is as shown below [2] .

(4.0)

The velocity vector is the velocity of each individual charged particle in the cloud density being accelerated by vector valued electromagnetic force [2] . Where q is the individual charge of each particle in the cloud density. The x-component of particle velocity is given as approximated velocity value as shown below.

(4.01)

The vector value for the magnetic field is given such that:

(4.02)

The vector value for the electric field is given such that:

(4.03)

Carrying out the cross product of velocity vector and magnetic field vector give the orthogonal vector value shown below.

(4.04)

The value of Lorentz force vector at the given vector quantities of electric field, particle velocity, and magnetic field are that of Equation (4.05) below.

(4.05)

The magnitude of electromagnetic force vector () takes on a value such that:

(4.06)

The magnitude of electromagnetic force is set equal to force corresponding to pressure and cross sectional area (previously mentioned in section 1) to be acting on the cloud of charged particles as shown in Equation (4.07) below.

(4.07)

Recall that acceleration corresponds to the force () per unit area () acting on the cloud of accelerated charged particles, which correspond to pressure (where). Recall that force takes on a value such that:

(4.08)

The value of Equation (4.07) then becomes:

(4.09)

Equation (4.09) can be expressed such that:

(4.10)

The task is to obtain the required voltage at a given acceleration number, this will require one to solve Equation (4.10) for electric field E as shown below.

(4.11)

Recall that velocity is the particles’ approximate velocity at 99% of the speed of light. Thus, velocity is simply the product of the speed of light c and the value 0.99. The speed of light can then be distributed out of Equation (4.11), giving the value of Equation (4.12) such that:

(4.12)

The value of electrical field E is equal to the negative partial derivative of voltage V in respect to length x [2] .

(4.13)

Substituting this value (Equation (4.13)) into Equation (4.12) gives the differential equation shown below.

(4.14)

This can be rearranged such that:

(4.15)

The corresponding integrals in respect to voltage V and length x are expressed such that [2] :

(4.16)

where is unit length, evaluating the integrals give the value of voltage such that:

(4.17)

Length is set to unity (), therefore voltage can be expressed such that:

(4.18)

Voltage is the product of electrical current I and resistance R () [2] .

(4.19)

Equations ((4.18) and (4.19)) show the required voltage at acceleration number to produce gravitational force fields and the corresponding space-time curves using a given density number of charged particles at 99% if the speed of light. Thus the value of voltage or IR sufficient to produce an acceleration that will generate gravity can be shown to exist in the real world with the condition of the inequality below.

(4.20)

Voltage can be mapped to and corresponds to a gravitational force value at the number of particles and acceleration number as shown below.

(4.21)

where gravitational force is such that:

(4.22)

6. Conclusion: Experiment Proposal

The force associated with the Casimir effect describing vacuum energy was confirmed by an experiment conducted by physicist Steven Lamoreaux in 1996 [6] . The experiment was conducted in a vacuum between two metal plates [6] . The minutest value of force pulling the plates together was detected. Thus, in a similar manner, an experiment can be conducted where a cloud of charged particles are accelerated to within an infinitesimal fraction of the speed of light between two non-metal plates constructed of an electrically neutral material to avoid the detection of electromagnetic forces that can be confused with gravitational force. The equation of gravitational force linking gravitation to acceleration number and the number of particles can be used to predict a pressure () exerted on the electrically neutral plates. The experimental verification of the equations formulated in this paper will lead to further progress in generating gravitational fields and space-time curves based on any method of energy generation that produces electromagnetic energy used to sufficiently accelerate the charged particles. Lastly, the obvious implication to the generation of a gravitational field proportionally to energy produced is the possibility of generating artificial gravity without the use of centripetal force and the generation of space-time curves also science fictionally referred to as warp fields.

Cite this paper

Edward A. Walker, (2016) Gravitational Space-Time Curve Generation via Accelerated Charged Particles. Journal of Modern Physics,07,863-874. doi: 10.4236/jmp.2016.79078

References