Journal of Modern Physics
Vol.07 No.06(2016), Article ID:64680,2 pages
10.4236/jmp.2016.76047
A Note on the Expectation Value of Time
Yigal Ronen
Ben-Gurion University of the Negev, Be’er Sheba, Israel

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 January 2016; accepted 14 March 2016; published 17 March 2016
ABSTRACT
In this note, the expectation value of time based on quantum mechanics formalism is derived. It is found that the expectation value of time does not depend on space.
Keywords:
Expectation Value of Time, Space Dependence, Time Operator

1. Introduction
In this note, non-relativistic expectation value of time based on quantum mechanics formalism is derived. Aspects related to time, which are dealt with relativistic theories, are not considered in this note. Only quantum mechanics formalism is applied. Therefore, the validity of the presented results is subject to the validity of the non-relativistic assumption. The mathematical procedures used in this note are similar to the common ones in textbooks [1] , which are used to determine the constant of the motion in many physical laws.
2. Derivation of the Expectation Value of Time
The time operator 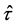 gives the time t when operates on the system wave function. Namely:
gives the time t when operates on the system wave function. Namely:
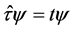 (1)
(1)
We chose the direction of the linear momentum in the x-direction. As a result, the wave function is presented as:
 (2)
(2)
The expectation value of time is related to the space by:
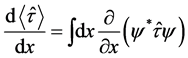 (3)
(3)
The change in space of the integrand of Equation (3) is given by:
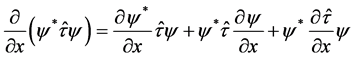 (4)
(4)
The relations between the space derivatives and the linear momentum are given by:
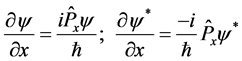 (5)
(5)
Introducing the space derivatives of Equation (5) into Equation (4), we will have:
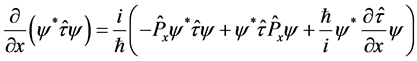 (6)
(6)
Integrating Equation (6) over space will give:
 (7)
(7)
Therefore, we receive:
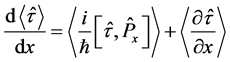 (8)
(8)
The time operator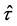 , which does not explicitly depend on space, is leading to:
, which does not explicitly depend on space, is leading to:
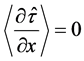 (9)
(9)
Since  is an operator, which does not depend on space, and the momentum operator
is an operator, which does not depend on space, and the momentum operator  does not depend on time, we have the operator
does not depend on time, we have the operator 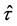 commutes with the operator
commutes with the operator 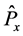 and the commutator
and the commutator

3. Summary and Conclusions
In this note, we have not considered relativistic effects. These effects are not considered either for obtaining constants of the motion variables (observables), which lead to conservation laws [1] .
The main conclusion of this note is that in systems that are determined by Quantum Mechanics formulations, the time expectation value does not change with space.
Cite this paper
YigalRonen, (2016) A Note on the Expectation Value of Time. Journal of Modern Physics,07,459-460. doi: 10.4236/jmp.2016.76047
References
- 1. Liboff, R.L. (1998) Introductory Quantum Mechanics. Addison-Wesley Longman, Inc., Reading.

