Received 21 September 2015; accepted 2 November 2015; published 5 November 2015

ABSTRACT

In a closed vacuum-dominated universe, the holographic principle implies that only a finite amount of information will ever be available to describe the distribution of matter in the sea of cosmic microwave background radiation. When z = 6 to z = 8, if information describing the distribution of matter in large scale structures is uniformly distributed in structures ranging in mass from that of the largest stars to the Jeans’ mass, a holographic model for large scale structure in a closed universe can account for massive galaxies and central black holes observed at z = 6 to z = 8. In sharp contrast, the usual approach assuming only collapse of primordial overdensities into large scale structures has difficulty producing massive galaxies and central black holes at z = 6 to z = 8.

Keywords:

Large Scale Structure, Holography, Early Galaxies, Early Supermassive Black Holes

1. Introduction

“Current theory predicts that galaxies begin their existence as tiny density fluctuations, with overdensities collapsing into virialized protogalaxies, and eventually assemble gas and dust into stars and black holes” [1] . Steinhardt et al. [1] summarized data indicating that the current approach had difficulty accounting for massive galaxies and their associated central black holes at redshifts 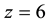to.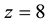

To address the “impossibly early galaxy problem” of Steinhardt et al., this analysis treats our universe as a closed Friedmann universe, dominated by vacuum energy in the form of a cosmological constant, and so large that it is approximately flat. This is consistent with full mission 2015 Planck satellite observations [2] indicating that the universe is dominated by vacuum energy, spatially flat to a good approximation, with Hubble constant, total matter density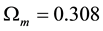, and baryonic density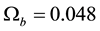. Adler and Overduin [3] claimed “observation cannot distinguish―even in principle―between a perfectly flat universe and one that is sufficiently close to flat.” However, analysis assuming a closed inflationary universe and accounting for important features of large scale structure may indicate that our universe is closed.

In the following, 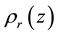is the cosmic microwave background (CMB) radiation density at redshift z, where 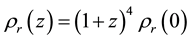and the mass equivalent of today’s radiation energy density 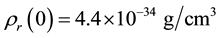[4] , the matter density at redshift z is 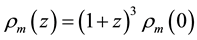where 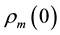is today’s matter density, and

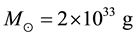is the solar mass. With Hubble constant, the critical density

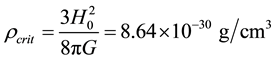, where 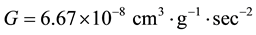and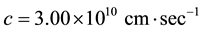. Since

matter accounts for 30.8% of the energy in today’s universe, and the vacuum energy density. The cosmological constant

and there is an event horizon in the universe at radius

. According to the holographic principle [5] , the number of bits of information available on the light sheets of any surface with area a is, where is the Planck length and is Planck’s constant. So, only bits of information on the event horizon will ever be available to describe our universe.

In a closed universe, there is no source or sink for information outside the universe, so the total amount of information available to describe the universe remains constant. Also, after the first few seconds of the life of the universe, energy exchange between matter and radiation is negligible compared to the total energy of matter and radiation separately [6] . Therefore, in a closed universe, the total quantity of matter in the universe is conserved; there is only a fixed amount of information available; and the average mass per bit of information is constant. In a closed, isotropic, and homogeneous Friedmann universe, the constant mass per bit of information

(the mass within the event horizon today divided by the number of bits of

information within the event horizon) is. So, the total mass within the event horizon today relates to the square of the event horizon radius by, where , giving the relation between mass within the event horizon and radius of a holographic screen just enclosing that mass.

2. Galaxies at z = 6 to z = 8

At, a hierarchical model of large scale structure can be developed using the holographic principle [7] , but the hierarchical model is not applicable at. So, the following analysis extends the ideas in Refs. [7] to consider large scale structure at.

When the matter density is much greater than the radiation density, the speed of pressure

waves affecting matter density is [8] , and the Jeans’ length is

[8] . The Jeans’ mass, the mass of matter within a radius one quarter of the Jeans’ wavelength, is, where. Since is independent of z, the Jeans’ mass is independ- ent of z, and there are Jean’s masses within the event horizon.

In this holographic model for large scale structure at, visible structures inhabit spherical isothermal halos of dark matter with masses ranging from that of the largest star to the Jeans’ mass, holographic radii

cm, the number of halos in mass bin given by, and the number of bits of information in any mass bin (proportional to) the same in all mass bins. Following Ref. [7] , this analysis

uses a maximum stellar mass of [9] coinciding with the estimated minimum stellar mass at and consistent with indications that the first stars formed at [10] . The mass within the event

horizon relates to the aggregate of halo masses by. So, , the number of halos within the event horizon is and the average halo mass is.

While recognizing the difficulties and intricacies involved in estimating halo masses at large redshift, Steinhardt et al. [1] present their estimates for the number of halos in a volume in their Figure 1. For comparison with those data, consider mass bins with width. Then, within the volume now enclosed by the event horizon, the number of halos with mass between and

is. Correspondingly, the number of halos with

mass between and is and the number of halos with mass

between and is.

The scale factor relates to today’s scale factor by. The volume within the event horizon today, , occupied a volume of at and a volume of

at. So, the volume within the event horizon today was at, and at. Considering mass bins with width, the number of halos per and the logarithm of that density expected from this holographic model for and are shown below.

Compared to the cloud of data points in Figure 1 of Steinhardt et al. [1] showing their estimated halo densities, the above results are slightly below the cloud at, just below the lower edge of the cloud at, and at the upper edge of the cloud at. So, halo densities similar to those estimated from observations at to are an inevitable consequence of the holographic anlysis outlined above.

3. Black Holes at z = 6 to z = 8

As in Ref. [7] , it is assumed an isothermal spherical halo of dark matter with mass M_S is enclosed by a holo-

graphic screen with radius cm. The isothermal halo matter density distribution is,

where r is the distance from the center of the halo and a is constant. The mass within the holographic

radius R_s in an isothermal density distribution is, requiring. The mass within radius R from the center of a halo is.

If the mass of the central supermassive black hole (SMBH) is at the center of a core volume with radius equal to the holographic radius of stars with the maximum stellar mass, stars of all masses can orbit the center of the structure just outside the core without their holographic screens encountering the central black hole so they would be disrupted and drawn into the central black hole. The resulting SMBH mass estimate is

, where is the total halo mass and is the maximum stellar mass.

Mortlock et al. [11] found a black hole with mass at in the quasar ULAS J1120+ 0641. Pacucci, Volonteri, and Ferrara [12] , noting evidence for supermassive black holes in the to range only 10⁹ years after the Big Bang, recognize this “evidence contrasts with the standard theory of black hole growth.” In comparison, the average halo mass at z = 6 to z = 8 in this holographic model is and the corresponding central black hole mass is, similar to the mass of the black hole in ULAS J1120 + 0641.

4. Conclusion

Caltech’s Professor Steinhardt and colleagues [1] discussed the “impossibly early galaxy problem,” reviewing data showing that the conventional approach to formation of large scale structure cannot adequately account for presence of the massive galaxies and associated central black holes observed at redshifts z = 6 to z = 8. In sharp contrast, the holographic analysis outlined above requires supermassive black holes with mass on the order of at z = 6 to z = 8. This is consistent with the observations of Trakhtenbrot et al. [13] indicating the presence of a black hole with mass in the AGN (active galactic nucleus) CID-947 at.

Cite this paper

T. R.Mongan, (2015) Massive Galaxies and Central Black Holes at z = 6 to z = 8. Journal of Modern Physics,06,1987-1990. doi: 10.4236/jmp.2015.614204

References