Journal of Modern Physics
Vol.07 No.04(2016), Article ID:63919,6 pages
10.4236/jmp.2016.74036
Quantum Mechanical Path Integral in Phase Space and Class of Harmonic Oscillators with Varied Frequencies
B. Berrabah
Laboratoire de Physique Mathmatique et Subatomique (LPMPS), Constantine 1 University, Constantine, Algeria

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 August 2015; accepted 23 February 2016; published 26 February 2016
ABSTRACT
We present the problem of the time-dependent Harmonic oscillator with time-dependent mass and frequency in phase space and by using a canonical transformation and delta functional integration we could find the propagator related to the system. New examples of time-dependent frequencies are presented.
Keywords:
Phase Space, Canonical Transformations, Propagator, Time-Dependent Harmonic Oscillator

1. Introduction
Recently, a great deal of attention has been paid to the subject of time dependent Hamiltonians. The importance of this problem in various areas of physics, quantum optics [1] , cosmology [2] , nanotechnology [3] and plasma physics [4] is the main reason for these intensive studies. The harmonic oscillator with time-dependent mass and frequency is a common problem in this area, and it is very important system, because we can find it in many physical areas. Abdalla and Colograve [5] -[7] studied this problem with a time dependent mass and constant frequency in order to describe the electromagnetic field intensities in a Fabry-Poerot cavity by applying a time dependent canonical transformation. The problem also has been treated using the time-dependent dynamical invariant by Lewis and Riesenfeld [8] . Kandekar and Lawand [9] have considered the case of exponentially varying mass with variable frequency by means of path integral method. The same problem with a constant frequency has been treated by path integral by many authors for example: Sabir and Rajagopalan [10] treated the cases of the strongly pulsating mass and a model of growing mass, the power-low suppressed harmonic oscillator [11] is also solved. In [12] the problem with an arbitrary time dependent mass and frequency is treated using space-time transformations. The same problem has been solved in [13] . Cheng [14] evaluated the propagator of a forced time dependent harmonic oscillator.
Looking through the literature one can find that an explicit expression for the propagator could not be obtained for all time varying mass-functions or frequencies because the procedure involves the solutions of non- linear differential equations. This is the reason why the literature is not reached by many exactly evaluated systems, which has many applications in physics [1] - [4] [15] [16] . Only few cases of varying mass and frequency have been solved, as mentioned above the strongly pulsating mass [7] , the exponentially time-dependent mass [17] , the power-low mass [11] and some examples are given in [18] - [20] .
In this paper we will present a way to find the propagators of the time dependent harmonic oscillators in phase space using canonical transformations and delta functional integration [21] . As an application of that we will follow by a class of time dependent harmonic oscillators with time-dependent frequencies we think and see that they have exact propagators.
2. The Harmonic Oscillator and the Propagator
Let us present the following time dependent Hamiltonian [17]
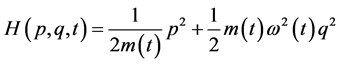 (1)
(1)
The propagator corresponds to this system can be written in the phase space as
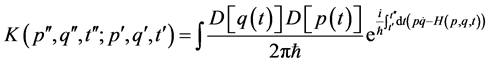 (2)
(2)
This propagator is not exactly evaluated for any arbitrary time dependent mass or frequency, because that will lead to non-linear differential equations. To deal with this system we will absorb the quadratic term of q, by taking the following transformation
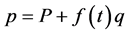 (3)
(3)
where 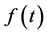 is an arbitrary function. The propagator (2) under this transformation will have the following form
is an arbitrary function. The propagator (2) under this transformation will have the following form
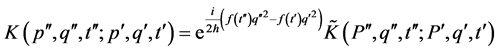 (4)
(4)
where 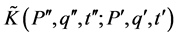 is the propagator that has the following expression
is the propagator that has the following expression
 (5)
(5)
and the new Hamiltonian 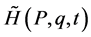 is
is
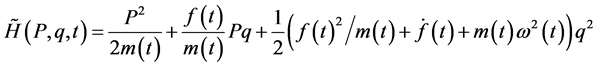 (6)
(6)
Since  is an arbitrary function we will choose it such that the quadratic term in the new Hamiltonian disappears
is an arbitrary function we will choose it such that the quadratic term in the new Hamiltonian disappears
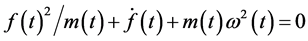 (7)
(7)
Then 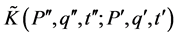 will be
will be
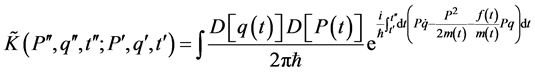 (8)
(8)
to deal with this propagator we will take the following canonical transformations
 (9)
(9)
With the generating function 

Then (8) will be (see [22] )

Since 

In the exponent and by integrating the first term by part, then following by the integration over q we get the following condition

which implies that 

Using the formula

one can finds that

By inserting this into Equation (4) we will find the expression of the propagator related to Equation (1)

which is the desired result
3. The Models
We would like to present a class of time dependent Harmonic oscillators with constant mass and varied frequencies, and we will follow the way that given above to find the exact propagator of the related system. Let us present the following Hamiltonian

where 



Then the propagator related to this system can has the following expression

Then we will present the following canonical transformations

where P and q are the new momentum and position. This will lead to a new expression of the propagator Equation (20)

From here it is clear why the condition 
Examples
・
The related function for this frequency is
・
The related function for this frequency is
・
The related function for this frequency is
・
This frequency has a more generalized form than that given in [19] , where 


where r, v and t0 are constants with t0 has the dimension of time.
4. Summery
The problem of the time dependent harmonic oscillator has been presented in this work. By using canonical transformations we could reach Equation (11) with the condition Equation (2), then using delta functional integration that gave us the condition Equation (13) of the momentum conservation, which can be generalized to be 

Acknowledgements
We thank the Editor and the referee for their comments and support that is greatly appreciated.
Cite this paper
B.Berrabah, (2016) Quantum Mechanical Path Integral in Phase Space and Class of Harmonic Oscillators with Varied Frequencies. Journal of Modern Physics,07,359-364. doi: 10.4236/jmp.2016.74036
References
- 1. Colegrave, R.K. and Abdalla, M.S. (1981) Journal of Physics A: Mathematical and General, 14, 2269-2280.
http://dx.doi.org/10.1088/0305-4470/14/9/022 - 2. Berger, B.K. (1975) Physical Review D, 12, 368-375.
http://dx.doi.org/10.1103/PhysRevD.12.368 - 3. Brown, L.S. (1991) Physical Review Letters, 66, 527-529.
http://dx.doi.org/10.1103/PhysRevLett.66.527 - 4. Ben-Aryeh, Y. and Monn, A. (1985) Physical Review Letters, 54, 1020.
http://dx.doi.org/10.1103/PhysRevLett.54.1020 - 5. Colegrave, R.K. and Abdalla, M.S. (1981) Optica Acta, 28, 495-501.
http://dx.doi.org/10.1080/713820584 - 6. Colegrave, R.K. and Abdalla, M.S. (1983) Optica Acta, 30, 849-860.
http://dx.doi.org/10.1080/716099648 - 7. Colegrave, R.K. and Abdalla, M.S. (1983) Optica Acta, 30, 861-873.
http://dx.doi.org/10.1080/716099648a - 8. Lewis, H.R. and Riesenfeld, W.B. (1969) Journal of Mathematical Physics, 10, 1458-1473.
http://dx.doi.org/10.1063/1.1664991 - 9. Khndekar, D.C., Lawand, S.V. and Bhagwat, K.V. (1990) Path Integral Method and Their Applications. World Scientific, Singapore.
- 10. Sabir, M. and Rajagopalan, S. (1991) Pramana, 37, 253-260.
http://dx.doi.org/10.1007/BF02847479 - 11. Lewis Jr., H.R. and Riesenfeld, W.B. (1969) Journal of Mathematical Physics, 10, 1458.
http://dx.doi.org/10.1063/1.1664991 - 12. Um, C.I., Yeon, K.H., Choi, J.R., Kim, C.W. and George, T.F. (submitted) Physical Review A.
- 13. Nassar, A.B., Bassalo, J.M.F., Antunes Neto, H.S. and de Santos Alencar, P. (1986) Journal of Physics A General Physics, 19, L891-L893.
- 14. Cheng, B.K. (1983) Revista Brasileira de Física, 13, 220-230.
- 15. Harari, G., Ben-Aryeh, Y. and Mann, A. (2014) Physica Scripta, 90, Article ID: 074060.
- 16. Trypogeorgos, D. and Foot, C.J. (2014) A Two-Frequency Ion Trap Confining Ions with Widely Different Charge-to-Mass Ratios. arXiv:1310.6294v2 [physics.atom-ph].
- 17. Boudjema-Bouloudenine, M., Boudjedaa, T. and Makhlouf, A. (2006) The European Physical Journal C—Particles and Fields, 46, 807-816.
http://dx.doi.org/10.1140/epjc/s2006-02515-9 - 18. Cordero-Soto, R., Suazo, E. and Suslov, S.K. (2010) Annals of Physics, 325, 1884-1912.
http://dx.doi.org/10.1016/j.aop.2010.02.020 - 19. Grosche, C. (1993) Physics Letters A, 182, 28-36.
http://dx.doi.org/10.1016/0375-9601(93)90048-5 - 20. Uma, C.I., Yeonb, K.H. and George, T.F. (2002) Physics Reports, 362, 63-192.
http://dx.doi.org/10.1016/S0370-1573(01)00077-1 - 21. Anderson, A. and Anderson, S.B. (1990) Annals of Physics, 199, 155-186.
http://dx.doi.org/10.1016/0003-4916(90)90372-U - 22. Ahmedov, H., Duru, I.H. and Gumrukcuoglu, A.E. (2005) A Simple Path Integration for the Time Dependent Oscillator. arXiv:quant-ph/0511095v1.








